15. 光学文字認識 (OCR)
15.1 はじめに
あなたのコンピューターが皿洗いをして、洗濯をして、夕食を作って、部屋の掃除までしてくれたら? 家事の手伝いは誰もが歓迎することに違いない! しかし、コンピューターが人間と同じように家事を行うには何が必要になるだろうか?
高名な計算機科学者アラン・チューリングは、機械が人間と区別不能なレベルの知性を持つかどうかを判定するためのチューリングテストと呼ばれる手続きを考案した。チューリングテストでは人間の判定者が姿の見えない二つの存在 (一つは人間、もう一つは機械) と対話し、どちらが人間でどちらが機械かを見分けるよう指示される。もし判定者が機械と人間を見分けられなかったら、機械は人間レベルの知性を持つとみなされる。
チューリングテストで本当に知性を評価できるかどうか、そしてチューリングテストをパスする知性を持った機械を人間が作れるかどうかについては多くの議論がある。しかし、ある程度の知性を持った機械が存在することは確かである。例えばオフィス内を移動して簡単なタスクを行うロボットに搭載されるソフトウェアや、アルツハイマー病の進行を防止するためのソフトウェアがある。こういった AI (artificial intelligence, 人工知能) のより身近な例としては、Google の検索バーに何かを入力したときに出てくる予測キーワードや、Facebook のニュースフィードの内容を決める仕組みがある。
AI の有名な応用の一つが OCR (optical character recognition, 光学文字認識) である。OCR システムは手書き文字を入力として受け取り、それを機械が読めるテキストに変換する。手書きの小切手を銀行にある機械に入れるときには深く考えないかもしれないが、OCR には興味深い処理が関係する。本章では ANN (Artificial Neural Network, 人工ニューラルネットワーク) を使って実際に数字を認識できる簡単な OCR を作成する。ただ最初は、前提知識をもう少し説明しよう。
15.2 人工知能とは何か?
チューリングが示した知性の定義は合理的だと思うかもしれないが、結局のところ知性の構成要素は何かという問題は本質的に哲学的な議論の対象である。これに対して、計算機科学者はシステムとアルゴリズムを種類ごとに AI の分野として整理してきた。数多くある AI の分野の一部を次に示す:
- 事前に定義された世界の知識を用いた論理的および確率的な推論: 例えば、冷房が温度と湿度を確認して必要な場合に自動で運転を開始する機能にはファジー論理が使われている。
- ヒューリスティック探索: 例えば、チェスで次の最善手を求めるには、打てる手を可能な限り多く調べて最も良い盤面が得られる手を選択する。
- フィードバックモデルを持った機械学習: 例えば、OCR などのパターン認識問題がこれに該当する。
一般に、ML (machine learning, 機械学習) では識別するパターンをシステムに教え込むための訓練に大規模なデータセットが必要になる。この訓練データセットはラベル付き、つまり特定の入力に対してシステムに期待される出力が指定されている場合もあれば、期待される出力が指定されないラベルなしの場合もある。システムの訓練にラベル付きのデータを使うアルゴリズムは教師あり (supervised) と呼ばれ、ラベルなしのデータを使うアルゴリズムは教師なし (unsupervised) と呼ばれる。OCR システムの作成に使える ML のアルゴリズムや手法は多く知られており、その一つが本章で使う ANN である。
15.3 人工ニューラルネットワーク (ANN)
ANN とは何か?
ANN は情報をやり取りする相互接続されたノードからなるネットワークであり、その構造と機能は実際の生物の脳に存在する神経ネットワークに着想を得ている。Hebbian Theory は、そういったネットワークが自身の構造や接続の強さを物理的に変化させることで特定のパターンを認識できるように学習する仕組みを説明する。同様に、典型的な ANN (図 1) はノードの接続が重みを持ち、ネットワークが学習を進めると重みが更新される。「+1」と書かれたノードはバイアス (bias) と呼ばれる。左端にある青い丸が入力ノード (input node) を表し、中央にあるオレンジ色の丸が隠れノード (hidden node) を、右端にあるオレンジ色の丸が出力ノード (output node) を表す。隠れノードの列がいくつも存在する ANN も可能であり、隠れノードの列全体を隠れ層 (hidden layer) と呼ぶ。
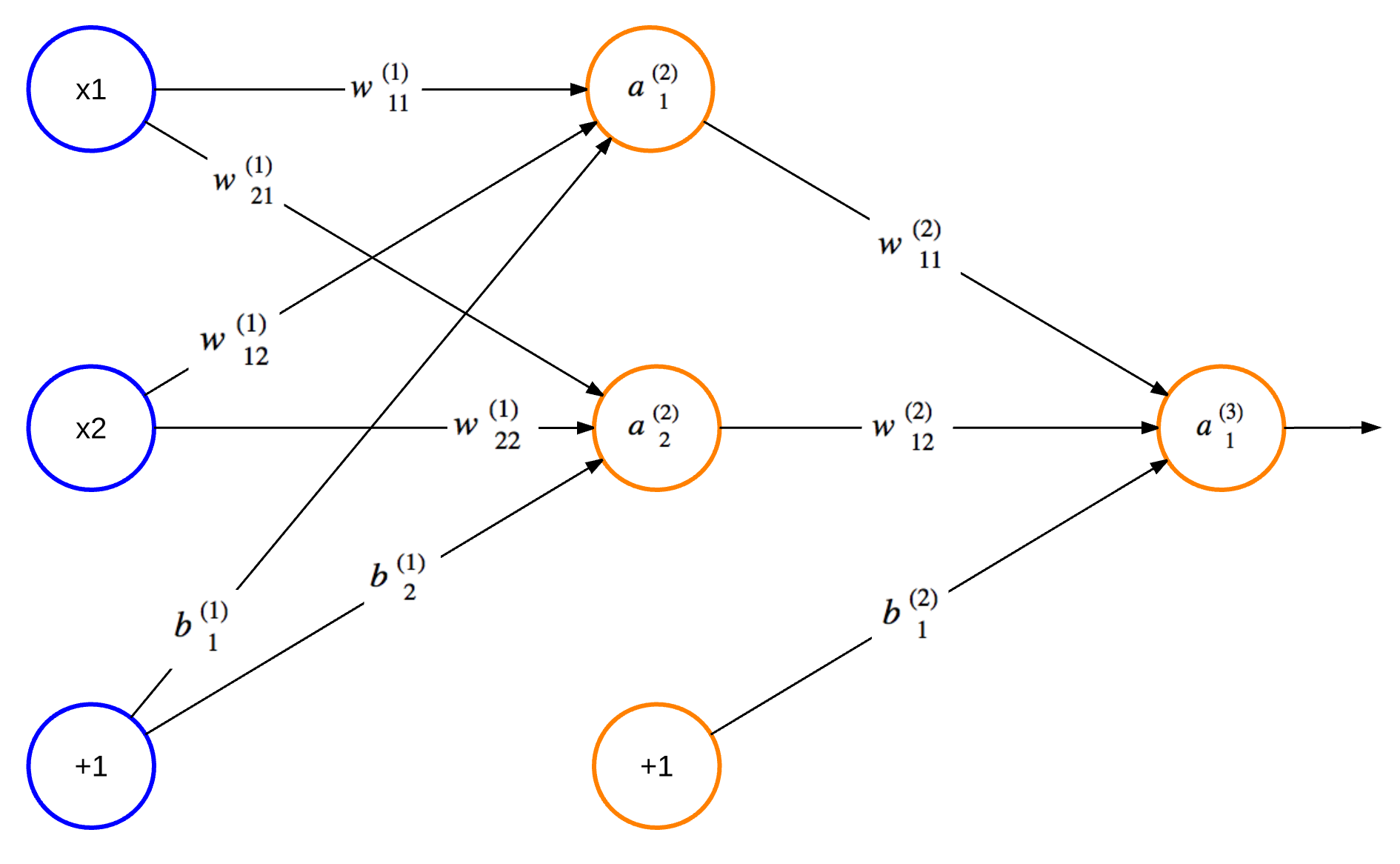
図 1 で円の中に記された値はノードの出力を表す。入力層を除く \(L\) 番目の層の上から \(n\) 番目のノードの出力を \(a^{(L)}_n\) と表し、\(L\) 番目の層の上から \(i\) 番目のノードと \(L + 1\) 番目の層の上から \(j\) 番目のノードを結ぶ接続の強さを \(w^{(L)}_{ji}\) と表すことにすれば、図 1 の \(2\) 番目の層の上から \(2\) 番目のノードの出力 \(a^{(2)}_2\) は次のように表せる:
ここで \(f(\cdot)\) は活性化関数 (activation function) を表し、\(b\) はバイアスを表す。活性化関数はノードの出力を決定する関数である。バイアスは正解率を向上させるために ANN に追加されるノードであり、常に \(1\) の出力を持つ。詳しくは後述される。
図 1 のように閉路を持たないトポロジーを持つ ANN を順伝播型 (feedforward) ニューラルネットワークと呼ぶ。一方で、自身の出力が自身の入力になるノードを持つ ANN を回帰型 (recurrent) ニューラルネットワークと呼ぶ。順伝播型 ANN を訓練するためのアルゴリズムは数多く知られている。広く使われるアルゴリズムの一つが誤差逆伝播法 (backpropagation) であり、本章で実装する OCR システムは誤差逆伝播法を用いる。
どのように ANN を使うか?
ML を利用する多くのアプローチと同様に、誤差逆伝播法を使う上での最初の一歩は考えている問題を ANN が解決できる形に変換または単純化することである。言い換えれば、どうすれば入力データを ANN に入力できるように変形できるだろうか? 私たちが考えている OCR システムでは、与えられた一桁の数字を表す画像を構成するピクセルの配列を入力として利用できる。入力データのフォーマットの選択がこれほど単純でない問題もあることは言及に値する。例えば、大きな画像を解析して何らかの形状を特定する問題では、輪郭線を特定する前処理を適用した画像を ANN に入力する必要があるかもしれない。
入力データのフォーマットが決まったら、次は? 誤差逆伝播法は教師あり学習のアルゴリズムなので、先述したように訓練にはラベル付きのデータが必要になる。つまりピクセルの配列を訓練用の入力として渡すとき、それに対応する一桁の数字も渡さなければならない。これは、手書きの一桁の数字の画像とそれが表す数字の組からなる大きなデータセットを収集しなければならないことを意味する。
続いて、収集されたデータセットは訓練セット (training set) と検証セット (validation set) に分割される。訓練セットは誤差逆伝播法アルゴリズムを実行して ANN の重みを設定するときに利用され、検証セットは訓練されたネットワークを評価するときに利用される。誤差逆伝播法と他の手法の性能を比較するときは、次のようにデータセットを分割すべきとされる。すなわち、データセットの 50% を訓練に使い、25 % を二つのアルゴリズムの性能比較に使い、最後の 25% を選択されたアルゴリズムの性能測定に使う。私たちはアルゴリズムを比較しているわけではないので、データセットの 75% で ANN を訓練し、残りの 25% で訓練結果を検証する。
ANN の正解率を測定する目的は二つある。一つ目の目的は過学習 (overfitting) と呼ばれる問題を検出することである。過学習とは、学習後の ANN が訓練セットに対しては高い正解率を示すにもかかわらず、検証セットに対しては正解率がずっと低くなる現象を言う。過学習が起きるとき訓練後の ANN は一般的な問題に対応できていないので、学習プロセスや訓練セットに調整が必要となる。次に、隠れ層の個数を変えたときの正解率は、最適な ANN のサイズを設計する上で役立つ情報となる。ANN は正確な予測ができるだけの隠れ層を持ちつつも、訓練と予測の計算オーバーヘッドを抑えるためにノードと接続を最小限だけ持つのが望ましい。最適なサイズの ANN が訓練できたら、予測を行う準備が整う!
15.4 簡単な OCR システムに関する設計判断
これまでの数段落で、順伝播型 ANN とその使い方の基本的な部分を説明した。続いて OCR システムの作り方を議論しよう。
まず、これから作るシステムができることを決めなければならない。簡単のため、ユーザーは一桁の数字を書き、その数字を使った訓練または予測を ANN に指示できるものとしよう。この OCR システムは単一のマシンでローカルに実行されるものの、クライアントとサーバーを分離すれば柔軟性が増すだろう。ANN の訓練のクラウドソーシングが可能になり、訓練に必要な計算を高性能なサーバーに任せられるようになる。
私たちの OCR システムは五個の主要な構成要素を持ち、それぞれが一つのファイルで実装される:
- クライアント (
ocr.js) - サーバー (
server.py) - 簡単なユーザーインターフェース (
ocr.html) - ANN モジュール(
ocr.py) - ANN 設計スクリプト (
neural_network_design.py)
ユーザーインターフェースは簡単なものであり、数字を書くためのキャンバス、そして ANN に訓練または予測を指示するためのボタンから構成される。クライアントはユーザーが書いた画像を取得して配列に変換し、それを訓練サンプルまたは予測リクエストとしてサーバーに送信する。これを受け取ったサーバーは訓練または予測を実行するために ANN モジュールの API を呼び出す。ANN モジュールは初回起動時に既存のデータセットを使って ANN を訓練して最終的な重みをファイルに書き込み、以降の呼び出しではファイルに書き込まれた重みを再利用する。訓練と予測に関する中心的なロジックを実装するのが ANN モジュールである。最後に、ANN 設計スクリプトは隠れ層の個数を変化させて最適な個数を求めるために利用される。これらの要素によって、非常に簡単ではあるものの確かに機能する OCR システムが構成される。
システムの動作を高いレベルで思い描いたら、次はアイデアを実現するコードを書こう!
簡単なインターフェース (ocr.html)
先述したように、最初のステップはネットワークを訓練するためのデータ収集である。ユーザーが手書きした数字の画像ファイルをサーバーにアップロードする方法も考えられるが、使いやすいとは言えない。HTML の canvas 要素を使ってユーザーが数字を直接手書きできるようにした方が便利だろう。ユーザーは書いた数字を使って ANN の訓練または ANN を使った予測を実行でき、ANN を訓練するときは書いた数字を指定する。こうしておけば、入力を送信するウェブサイトを変更することで簡単にデータ収集をアウトソースできる。インターフェースを定義する HTML を次に示す:
<html>
<head>
<script src="ocr.js"></script>
<link rel="stylesheet" type="text/css" href="ocr.css">
</head>
<body onload="ocrDemo.onLoadFunction()">
<div id="main-container" style="text-align: center;">
<h1>OCR Demo</h1>
<canvas id="canvas" width="200" height="200"></canvas>
<form name="input">
<p>Digit: <input id="digit" type="text"> </p>
<input type="button" value="Train" onclick="ocrDemo.train()">
<input type="button" value="Test" onclick="ocrDemo.test()">
<input type="button" value="Reset" onclick="ocrDemo.resetCanvas();"/>
</form>
</div>
</body>
</html>
OCR クライアント (ocr.js)
HTML の canvas 要素に表示されるピクセルは非常に小さいので、ANN に対する入力では 10x10 のピクセルを一単位として扱う。つまり、canvas 要素が 200x200 ピクセルのとき ANN は 20x20 のデータを入力に受け取る。こういった数値を管理するための変数が次のように定義される:
var ocrDemo = {
CANVAS_WIDTH: 200,
TRANSLATED_WIDTH: 20,
PIXEL_WIDTH: 10, // TRANSLATED_WIDTH = CANVAS_WIDTH / PIXEL_WIDTH
...
}
これらの定数を使えば、ANN が canvas 要素の内容をどのように「見る」かを表す格子を描画できる。この処理は drawGrid 関数が行う:
drawGrid: function(ctx) {
for (var x = this.PIXEL_WIDTH, y = this.PIXEL_WIDTH;
x < this.CANVAS_WIDTH; x += this.PIXEL_WIDTH,
y += this.PIXEL_WIDTH) {
ctx.strokeStyle = this.BLUE;
ctx.beginPath();
ctx.moveTo(x, 0);
ctx.lineTo(x, this.CANVAS_WIDTH);
ctx.stroke();
ctx.beginPath();
ctx.moveTo(0, y);
ctx.lineTo(this.CANVAS_WIDTH, y);
ctx.stroke();
}
},
続いて、この格子に書かれたデータをサーバーに送信できる形式に格納する必要がある。簡単のため、data と呼ばれる配列を用意して、黒色のピクセルを 0 で表し、白色のピクセルを 1 で表すことにする。また、ユーザーが書いた通りにピクセルを白色にするマウス関連のイベントリスナーも定義が必要になる。特定のピクセルを白色にして data を更新する処理は fillSquare 関数が実行する:
onMouseMove: function(e, ctx, canvas) {
if (!canvas.isDrawing) {
return;
}
this.fillSquare(ctx,
e.clientX - canvas.offsetLeft, e.clientY - canvas.offsetTop);
},
onMouseDown: function(e, ctx, canvas) {
canvas.isDrawing = true;
this.fillSquare(ctx,
e.clientX - canvas.offsetLeft, e.clientY - canvas.offsetTop);
},
onMouseUp: function(e) {
canvas.isDrawing = false;
},
fillSquare: function(ctx, x, y) {
var xPixel = Math.floor(x / this.PIXEL_WIDTH);
var yPixel = Math.floor(y / this.PIXEL_WIDTH);
this.data[((xPixel - 1) * this.TRANSLATED_WIDTH + yPixel) - 1] = 1;
ctx.fillStyle = '#ffffff';
ctx.fillRect(xPixel * this.PIXEL_WIDTH, yPixel * this.PIXEL_WIDTH,
this.PIXEL_WIDTH, this.PIXEL_WIDTH);
},
楽しい部分までもう少しだ! 次はサーバーに送信する訓練データを準備する関数を書こう。次の train 関数は比較的単純な実装であり、ユーザーが入力したデータに対して簡単なエラーチェックを行い、それを trainArray に追加し、sendData 関数でサーバーに訓練データを送信する。
train: function() {
var digitVal = document.getElementById("digit").value;
if (!digitVal || this.data.indexOf(1) < 0) {
alert("Please type and draw a digit value in order to train the network");
return;
}
this.trainArray.push({"y0": this.data, "label": parseInt(digitVal)});
this.trainingRequestCount++;
// 訓練バッチをサーバーに送信する。
if (this.trainingRequestCount == this.BATCH_SIZE) {
alert("Sending training data to server...");
var json = {
trainArray: this.trainArray,
train: true
};
this.sendData(json);
this.trainingRequestCount = 0;
this.trainArray = [];
}
},
このコードが持つ注目に値する興味深い設計として、変数 trainingRequestCount, trainArray, BATCH_SIZE の利用がある。集まった訓練データの個数が事前に定義された BATCH_SIZE に等しくなるまでクライアントは訓練データをサーバーに送信しない。こうしてリクエストをバッチ化する主な理由は、大量のリクエストが同時にサーバーに向かう事態を避けるためである。多くのクライアントが存在する (ocr.html ページを開いて OCR システムを訓練しようとするユーザーが多くいる) とき、あるいはクライアントがデータを別のレイヤーに通してからサーバーに送信するときは、BATCH_SIZE が 1 だと不必要なリクエストが大量に発生する。このバッチ化の仕組みはクライアントの柔軟性を高めるためにある。実際のシステムでは、サーバーにもバッチ化が必要になる可能性がある。例えば、悪意あるクライアントが意図的に大量のリクエストをサーバーに送信する DoS 攻撃 (denial-of-service attack) を受けるかもしれない。
ANN を使った予測を実行する test 関数も存在する。train 関数と同様に、この関数はデータの正当性を簡単にチェックしてからサーバーにリクエストを送信する。ただし、ユーザーは予測を実行するボタンを押した後なるべく早く予測結果を確認したいはずなので、この test 関数ではバッチ化の処理が存在しない。
test: function() {
if (this.data.indexOf(1) < 0) {
alert("Please draw a digit in order to test the network");
return;
}
var json = {
image: this.data,
predict: true
};
this.sendData(json);
},
最後に、HTTP の POST メソッドを実行する関数、レスポンスを受け取る関数、その中で発生する可能性のあるエラーに対処する関数を定義する:
receiveResponse: function(xmlHttp) {
if (xmlHttp.status != 200) {
alert("Server returned status " + xmlHttp.status);
return;
}
var responseJSON = JSON.parse(xmlHttp.responseText);
if (xmlHttp.responseText && responseJSON.type == "test") {
alert("The neural network predicts you wrote a \'"
+ responseJSON.result + '\'');
}
},
onError: function(e) {
alert("Error occurred while connecting to server: " + e.target.statusText);
},
sendData: function(json) {
var xmlHttp = new XMLHttpRequest();
xmlHttp.open('POST', this.HOST + ":" + this.PORT, false);
xmlHttp.onload = function() { this.receiveResponse(xmlHttp); }.bind(this);
xmlHttp.onerror = function() { this.onError(xmlHttp) }.bind(this);
var msg = JSON.stringify(json);
xmlHttp.setRequestHeader('Content-length', msg.length);
xmlHttp.setRequestHeader("Connection", "close");
xmlHttp.send(msg);
}
サーバー (server.py)
私たちのシステムが持つサーバーは情報を転送するだけの単純な機能しか持たないものの、HTTP リクエストの送受信方法については少し考える必要がある。まず、どの HTTP メソッドを使うべきかを考えよう。前節ではクライアントが POST メソッドを使うと説明した。なぜそうしたのだろうか? データをサーバーに送信するところから考えると PUT と POST が適しているように思える。また、突き詰めれば URL にパラメータを付けずに JSON を送信しているだけなので理論的には GET リクエストも利用できるものの、意味論的には意味をなさない。PUT と POST の使い分けはプログラマーの間で議論が長く続いている話題である。この話題は KNPLabs によるユーモアたっぷりの記事にまとめられている。
別の懸念事項として、訓練と予測で異なるエンドポイント (例えば http://localhost/train と http://localhost/predict) を使うべきか、それとも同じエンドポイントを使って処理を分けるべきかという問題がある。本プロジェクトでは後者のアプローチを用いる。なぜなら、二つの処理の違いは簡単な if で判別できる程度に小さいからである。実際のシステムでは、サーバーの処理が単純な if より多くなった時点でリクエストの種類ごとにエンドポイントを用意するのが望ましい。この決定はサーバーが返すエラーコードとそのタイミングにも影響を及ぼす。例えば 400 Bad Request エラーは "train" と "predict" のいずれも指定されなかったときに返される。仮に個別のエンドポイントを使っていたとしたら、このエラーは発生しない。サーバーからの指示を受けて OCR システムが実行する処理は失敗する可能性があり、その失敗にサーバーが対処できないときは 500 Internal Server Error が返される。仮にエンドポイントが分かれていたら、ここで失敗の詳細を調べてより適切なエラーを返せる可能性がある。例えば、処理の失敗はリクエストの形式が間違っているために起きたのかもしれない。
最後に、OCR システムを初期化するタイミングと場所を決める必要がある。優れたアプローチは server.py の中でサーバーが処理を開始する前に初期化するというものである。OCR システムが初期化時に実行する事前に用意されたデータを使った ANN の訓練には、数分単位の時間がかかる可能性がある。この訓練が完了していないときに訓練または予測のリクエストを受け取ると、OCR オブジェクトが初期化されていないので現在の実装では例外が送出される。異なる実装の選択肢として、最初のうちは正解率の低い ANN を使っておいて、バックグラウンドで非同期に実行される訓練が完了したら新しい (優れた) ANN に入れ替える実装も考えられる。このアプローチには ANN がすぐに利用可能になる利点があるものの、その利点はサーバーが再起動したときにしか意味を持たず、実装も複雑になる。この種の実装は高可用性を必要とする OCR サービスで重要となるだろう。
サーバーコードの大部分は POST メソッドを処理する次の短い関数である:
def do_POST(s):
response_code = 200
response = ""
var_len = int(s.headers.get('Content-Length'))
content = s.rfile.read(var_len);
payload = json.loads(content);
if payload.get('train'):
nn.train(payload['trainArray'])
nn.save()
elif payload.get('predict'):
try:
response = {
"type":"test",
"result":nn.predict(str(payload['image']))
}
except:
response_code = 500
else:
response_code = 400
s.send_response(response_code)
s.send_header("Content-type", "application/json")
s.send_header("Access-Control-Allow-Origin", "*")
s.end_headers()
if response:
s.wfile.write(json.dumps(response))
return
順伝播型 ANN の設計 (neural_network_design.py)
順伝播型 ANN の設計では考慮すべき点がいくつかある。まず、利用する活性化関数の選択がある。ノードが入力から出力を決定するときに使う関数が活性化関数だと以前に説明した。活性化関数の選択では、ノードの出力の種類に注目すると見通しが立ちやすくなる。本プロジェクトで設計する ANN の最終的な出力は \(0\) から \(9\) までの整数それぞれに対する \(0\) から \(1\) の実数であり、\(1\) に近い値は対応する数字の可能性が高いことを、\(0\) に近い値は可能性が低いことを表す。よって、\(0\) に近い値と \(1\) に近い値を出力しやすい関数が活性化関数として望ましい。また、誤差逆伝播法を使うには活性化関数が微分可能である必要もある。こういった場合には、両方の条件を満たすシグモイド (sigmoid) と呼ばれる関数がよく使われる。StatSoft には有名な活性化関数とその特徴についての便利なリストが載っている。
次に、バイアスを追加するかどうかの選択がある。これまでバイアスには何度か言及したものの、具体的な説明や使う理由の説明は避けてきた。これから図 1 でノードの出力がどのように計算されるかをもう一度考えることで、そういった点を理解しよう。ノードが一つの入力と一つの出力を持つとき、その出力は \(y = f(wx)\) と表せる。ここで \(y\) は出力、\(f(\cdot)\) は活性化関数、\(w\) は自身と次のノードを結ぶ接続の重み、\(x\) は入力を表す。バイアスは出力が常に \(1\) のノードみなせる。よってバイアスがあるとき、バイアスとノードを結ぶ接続の重みを \(b\) とすれば、ノードの出力は \(y = f(wx + b)\) となる。\(w\) と \(b\) を定数、\(x\) を変数とみなせば、バイアスは活性化関数 \(f(\cdot)\) に対する線形入力に定数を加えていると解釈できる。
よってバイアスを加えると活性化関数に対する入力の \(y\) 切片が変化し、ノードの出力が持つ柔軟性が増す。特に入力と出力の個数が少ない ANN では、バイアスを含めた方が優れた結果が得られる可能性が高いとされている。バイアスがあると ANN の出力が柔軟になり、正解に手が届く可能性が高まる。バイアスを持たない ANN では予測が正しい確率が低下し、正確な予測に多くの隠れノードが必要になるだろう。
他に考えるべき要素として、隠れ層の個数と隠れ層ごとの隠れノードの個数がある。多くの入力と出力を持つ大規模な ANN では、これらの個数は異なる値を設定したときの ANN の性能テストを通して決める必要がある。本プロジェクトであれば、特定のサイズの ANN を訓練した後の検証セットに対する正解率が性能となる。多くのケースでは隠れ層が一つあればそれなりの性能が出るので、ここでは隠れ層は一つに固定して隠れノードの個数だけを変化させる:
# 隠れノードの個数を変化させて、どれが最も高い性能を示すかを調べる。
for num_hidden_nodes in xrange(5, 50, 5):
performance = str(test(data_matrix, data_labels, test_indices, num_hidden_nodes))
print "{i} Hidden Nodes: {val}".format(i=i, val=performance)
上記のコードでは ANN に含まれる隠れノードの個数を \(5\) から \(50\) まで \(5\) ずつ変化させている。呼び出されている test 関数は次の通りである:
def test(data_matrix, data_labels, test_indices, num_hidden_nodes):
avg_sum = 0
for j in range(100):
nn = OCRNeuralNetwork(num_hidden_nodes, data_matrix, data_labels, train_indices, False)
correct_guess_count = 0
for i in test_indices:
test = data_matrix[i]
prediction = nn.predict(test)
if data_labels[i] == prediction:
correct_guess_count += 1
avg_sum += (correct_guess_count / float(len(test_indices)))
print(correct_guess_count)
return avg_sum / 100
内部のループでは correct_guess_count が正しく識別されたデータの個数を数え、そのループを抜けると correct_guess_count がテストされたデータの個数で割られて正解率が計算される。ANN の重みは訓練のたびに少しずつ異なるので、このプロセスを 100 回繰り返すことで特定の ANN の設定が示す正解率の平均を計算する。neural_network_design.py の実行結果の一例を示す:
PERFORMANCE
-----------
5 Hidden Nodes: 0.7792
10 Hidden Nodes: 0.8704
15 Hidden Nodes: 0.8808
20 Hidden Nodes: 0.8864
25 Hidden Nodes: 0.8808
30 Hidden Nodes: 0.888
35 Hidden Nodes: 0.8904
40 Hidden Nodes: 0.8896
45 Hidden Nodes: 0.8928
この実行結果から、最適な隠れノードの個数は 15 だと結論できる。隠れノードの個数を 10 から 15 に増やすと約 1% の性能向上が得られるのに対して、そこから同じだけの性能向上を得るにはさらに 20 個の隠れノードを追加しなければならない。隠れノードを増やすと訓練・予測の計算量も増えるので、大きな性能向上が見られなくなった時点で隠れノードの追加は止めるべきである。もちろん、計算量が問題にならない状況では正解率が最も高い ANN を選ぶことが最優先となる。その場合は 15 個ではなく 45 個の隠れノードを利用した方がよい。
中心的な OCR 機能
本節では誤差逆伝播法を使った ANN の訓練、ANN を使った予測、そして中心的な機能に関する重要な設計判断について議論する。
誤差逆伝播法による訓練 (ocr.py)
本プロジェクトでは誤差逆伝播法と呼ばれるアルゴリズムを使って ANN を訓練する。このアルゴリズムは訓練セットの各サンプルを一つずつ見ていきながら四つのステップを通して ANN の重みを更新することで動作する。
まず、ANN の重みを小さな (\(-1\) から \(1\) の間の) 乱数で初期化する。ocr.py では \(-0.06\) から \(0.06\) の間の乱数で重みを初期化し、行列 theta1, theta2, input_layer_bias, hidden_layer_bias に保存する。特定の層に含まれるノードは必ず次の層に含まれるノードに接続するので、特定の二層間に存在する接続の重みは \(m\) 行 \(n\) 列の行列でまとめて表現できる。ここで \(n\) は最初の層に含まれるノードの個数を、\(m\) は次の層に含まれるノードの個数を表す。例えば theta1 は入力層と隠れ層の間に存在する接続の重みを表す行列であり、\(20\times20\) の入力に対応する \(400\) 個の列、そして隠れノードの個数に対応する num_hidden_nodes 個の行を持つ。同様に theta2 は隠れ層と出力層の間に存在する接続の重みを表す行列であり、num_hidden_nodes 個の列と NUM_DIGITS 個 (つまり \(10\) 個) の行を持つ。input_layer_bias と hidden_layer_bias はベクトルであり、バイアスノードが持つ接続の重みを表す。
def _rand_initialize_weights(self, size_in, size_out):
return [((x * 0.12) - 0.06) for x in np.random.rand(size_out, size_in)]
self.theta1 = self._rand_initialize_weights(400, num_hidden_nodes)
self.theta2 = self._rand_initialize_weights(num_hidden_nodes, 10)
self.input_layer_bias = self._rand_initialize_weights(1, num_hidden_nodes)
self.hidden_layer_bias = self._rand_initialize_weights(1, 10)
次のステップは順伝播 (forward propagation) と呼ばれる。この処理は層ごとに各ノードの出力を計算するのに等しい。以下のコードで data.y0 はANN を訓練するために入力された \(400\) 要素の配列を表す。まず theta1 と y0 の転置の乗算がある。乗じられる行列のサイズはそれぞれ (num_hidden_nodes x 400) と (400 x 1) なので、乗算結果のサイズは (num_hidden_nodes x 1) だと分かる。さらに各要素の計算過程を考えると、乗算結果は隠れノードの入力だと分かる。この入力にバイアスを足したものにシグモイドを適用すれば、隠れノードの出力からなるベクトル y1 が得られる。同じ処理を繰り返せば、出力ノードの出力からなるベクトル y2 が得られる: y2 の第 \(i\) 要素は、入力された画像が \(i\) である尤度を表す。例えばユーザーが \(8\) を書いて ANN の予測が正しいのなら、y2 の第 \(8\) 要素が最も大きくなる。このとき、y2 の第 \(6\) 要素は第 \(1\) 要素より値が大きい可能性が高い: \(6\) と \(1\) では \(6\) の方が \(8\) に形が近いからである。ANN を多くの訓練データで訓練していけば、その出力 y2 は正確になっていく。
# 活性化関数として使うシグモイド (スカラー)
def _sigmoid_scalar(self, z):
return 1 / (1 + math.e ** -z)
y1 = np.dot(np.mat(self.theta1), np.mat(data.y0).T)
sum1 = y1 + np.mat(self.input_layer_bias) # バイアスを加える。
y1 = self.sigmoid(sum1)
y2 = np.dot(np.array(self.theta2), y1)
y2 = np.add(y2, self.hidden_layer_bias) # バイアスを加える。
y2 = self.sigmoid(y2)
第三のステップは誤差逆伝播 (back propagation) と呼ばれる。まず、中間ノードを含めた全てのノードにおいて一つ前のステップで計算された予測結果と正しい値の差 (誤差) を計算する。このために、期待される解答を収めた完璧な出力ベクトル actual_vals が作成される。このベクトルは入力の画像が表す数字に対応する要素に 1 を持ち、その他の全ての要素に 0 を持つ。actual_vals から実際の出力ベクトル y2 を引くと出力ノードにおける誤差ベクトル output_errors が得られる。これより後ろの隠れ層では、二つの要素を計算する必要がある。まず、次の層の重み行列の転置に誤差ベクトルを乗じる。そして、一つ前の層からの入力に活性化関数の微分を適用する。両者を要素ごとに乗じると、隠れ層における誤差からなるベクトル hidden_errors が得られる。
actual_vals = [0] * 10
actual_vals[data.label] = 1
output_errors = np.mat(actual_vals).T - np.mat(y2)
hidden_errors = np.multiply(np.dot(np.mat(self.theta2).T, output_errors),
self.sigmoid_prime(sum1))
続いて、こうして計算された誤差を利用して ANN の重みを調整する。各層の重みの更新は行列の乗算を通して行われる。各層の誤差ベクトルと一つ前の層の出力行列の積に学習レート (learning rate) と呼ばれるスカラーを乗じた結果が重み行列に加算される。学習レートは \(0\) から \(1\) までの実数であり、ANN の学習の速度と正確性に影響する。学習レートを高くすると ANN の学習速度は向上するものの正確性は低下し、学習レートを低くすると学習速度は低下するものの正確性は向上する。本プロジェクトでは学習レートとして比較的小さい値 \(0.1\) を採用した。なぜなら、ANN の訓練が高速に完了しなくてもユーザーは訓練または予測のリクエストを送信できるからである。バイアスの更新は対応する層の誤差ベクトルと学習レートの積を加算することで行う。
self.theta1 += self.LEARNING_RATE * np.dot(np.mat(hidden_errors),
np.mat(data.y0))
self.theta2 += self.LEARNING_RATE * np.dot(np.mat(output_errors),
np.mat(y1).T)
self.hidden_layer_bias += self.LEARNING_RATE * output_errors
self.input_layer_bias += self.LEARNING_RATE * hidden_errors
ANN のテスト (ocr.py)
誤差逆伝播法による ANN の訓練が完了すれば、訓練結果の ANN を使った予測はとても簡単に実行できる。次のコードに示すように、誤差逆伝播のステップ 2 と同様の方法で ANN の出力 y2 を求め、y2 の最大要素の添え字を求めればよい。その添え字が ANN による予測結果となる。
def predict(self, test):
y1 = np.dot(np.mat(self.theta1), np.mat(test).T)
y1 = y1 + np.mat(self.input_layer_bias) # バイアスを加える。
y1 = self.sigmoid(y1)
y2 = np.dot(np.array(self.theta2), y1)
y2 = np.add(y2, self.hidden_layer_bias) # バイアスを加える。
y2 = self.sigmoid(y2)
results = y2.T.tolist()[0]
return results.index(max(results))
その他の設計判断 (ocr.py)
誤差逆伝播法の実装に関する詳しい解説はオンラインで多く公開されている。優れた資料の一つにウィラメット大学の講義ノートがある。この資料では、誤差逆伝播法の各ステップで実行される処理、そしてそれを行列形式に変換できる理由が説明される。行列を使う場合とループを使う場合で必要となる計算の量が変わるわけではないものの、行列を使うとコードがシンプルになり、入れ子になったループが減るので読みやすくなる。本章で示したように、行列があれば ANN の訓練処理を 25 行足らずで書くことができる。
本章の最初で言及した ANN の重みを永続化する処理があれば、サーバーがシャットダウンしたときや何らかの理由で突然動作を停止したときでも訓練後の ANN の重みを失わないで済む。重みの永続化では JSON が利用され、OCR システムは保存された ANN の重みを起動時にメモリへ読み込む。重みの永続化を実行する関数は OCR システム内部からは呼び出されず、永続化のタイミングはサーバーが指示する。現在の実装でサーバーは更新ごとに重みの永続化を実行する。これは簡単に実装できる単純な方法ではあるものの、ディスクへの書き込みには時間がかかるので最適とは言えない。また、同じファイルに対して同時に起こる複数の書き込みを調停する仕組みが存在しないので、現在の実装では複数のリクエストを並列に処理することもできない。より洗練されたサーバーでは、ロックやタイムスタンプを利用するプロトコルでデータが消失しないことを保証した永続化処理がシャットダウン時または数分おきに実行されるだろう。
def save(self):
if not self._use_file:
return
json_neural_network = {
"theta1":[np_mat.tolist()[0] for np_mat in self.theta1],
"theta2":[np_mat.tolist()[0] for np_mat in self.theta2],
"b1":self.input_layer_bias[0].tolist()[0],
"b2":self.hidden_layer_bias[0].tolist()[0]
};
with open(OCRNeuralNetwork.NN_FILE_PATH,'w') as nnFile:
json.dump(json_neural_network, nnFile)
def _load(self):
if not self._use_file:
return
with open(OCRNeuralNetwork.NN_FILE_PATH) as nnFile:
nn = json.load(nnFile)
self.theta1 = [np.array(li) for li in nn['theta1']]
self.theta2 = [np.array(li) for li in nn['theta2']]
self.input_layer_bias = [np.array(nn['b1'][0])]
self.hidden_layer_bias = [np.array(nn['b2'][0])]
15.5 結論
以上で私たちは AI、ANN、誤差逆伝播法、エンドツーエンドの OCR システムの作成方法について学んだ。最後に本章の内容と問題の全体像について振り返ろう。
本章では最初に AI と ANN に関する背景知識、そして実装する ANN の概形を説明した。AI とは何か、そして AI がどのように使われるかを議論した。AI とは人間と同様の形式で質問に対する解答を提供するアルゴリズムや問題解決アプローチの集合体であることを見た。その後、順伝播型 ANN を説明する中で、ANN のノードの出力は一つ前の層のノードの出力と接続の重みの積の和を活性化関数に通した結果だと学んだ。ANN を使うにあたっては、まず問題の入力を ANN が理解できる形式に変形し、データセットを訓練セットと検証セットに分ける必要があった。
基礎知識を一通り学んだ後は、OCR 用 ANN に対する訓練と予測をユーザーがリクエストできるウェブベースのクライアント・サーバーシステムを作る方法を議論した。クライアントスクリプトはユーザーが書いたピクセルを配列に変換し、OCR サーバーに対して HTTP リクエストを送信することで訓練または予測を実行する。単純なサーバーを使ってリクエストを処理する方法、そして隠れノードの個数を変化させたときの性能を確認して ANN を設計する方法を見た。最後に、誤差逆伝播法を使った ANN の訓練と ANN を使った OCR を実行するコアのコードを解説した。
こうして作成された OCR システムは一見すると十分な機能を持つように思えるものの、本章は実際の OCR システムが持つ機能の表面をなでただけに過ぎない。さらに高度な OCR システムは入力の事前処理を持ち、ハイブリッド ML アルゴリズムを利用し、拡張可能な設計フェーズを搭載し、様々な最適化を実装することだろう。