実際に動作する万歩計

完璧な世界

多くのソフトウェアエンジニアは、初学者だったころに感じた完璧な世界で物事を扱う高揚感を覚えているだろう。理想的なドメインにおいて厳密に定式化された問題を解く方法を最初に学んだはずである。

しかし勉強が終わって現実の世界に飛び込むと、そこら中に存在する厄介な問題や複雑性に嫌でも気が付く。そんな現実の世界で発生する問題を解くことができたなら、本当に人々の役に立つソフトウェアが作れたということになる。

本章では、一見すると簡単に見えるものの、現実の世界と現実の人間を考えると途端に難しくなる問題を考える。

本章で作成するのは簡単な歩数計である。最初に歩数計に関する理論を議論し、歩数の数え方をコードを使わないで考える。それから歩数を測定するコードを実装し、最後にユーザーが使いやすいインターフェースを持ったウェブレイヤーを追加する。

では袖をまくって、現実世界の問題に取り掛かる準備をしよう。

歩数計の理論

携帯機器が広まるにつれて、日常生活に関するデータを収集することがトレンドになった。多くの人が収集しているデータの一つが特定の時間に歩いた歩数である。このデータは健康状態の確認やスポーツイベントに向けた練習に利用でき、データの収集・解析マニアにとっても興味深い対象となる。歩数は歩数計で測定でき、多くの歩数計はハードウェア加速度計からのデータを入力として用いる。

加速度計とは何か？

加速度計 (accelerometer) とは、\(x\), \(y\), \(z\) 方向の加速度を測定するハードウェアである。現在販売されているほぼ全てのスマートフォンに搭載されているので、多くの人はどこへ行くにも加速度計を持ち歩いていることになる。測定で使われる \(x\), \(y\), \(z\) 方向は加速度計を基準とした座標である。

加速度計は三次元の信号 (signal) を返す。信号は特定の時間に集計されたデータ点の集合である。信号の各要素は時系列であり、それぞれが \(x\), \(y\), \(z\) 方向の加速度を表す。この時系列の各点は特定の時刻における対応する方向の加速度を表す。加速度は「\(\mathrm{G}\)」を一単位として測定される。\(1~\mathrm{G}\) は地球の重力加速度の平均値 \(9.8~\mathrm{m/s^2}\) に等しい。

加速度計から得られる信号に含まれる三つの時系列の例を図 1 に示す。

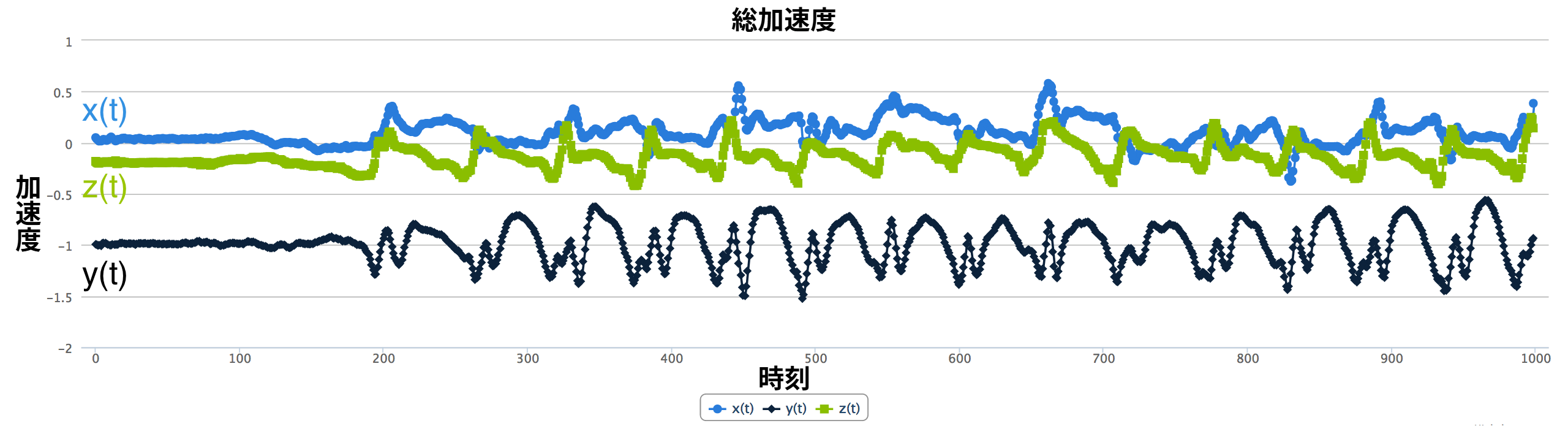
加速度計のサンプリングレート (sampling rate) とは、一秒間に行われる測定の回数を表す (調整可能である場合が多い)。例えば、サンプリングレートが \(100\) の加速度計は一秒間に \(x\), \(y\), \(z\) 方向の時系列ごとに \(100\) 個のデータ点を返す。

人間の歩行について

歩いている人間は、一歩ごとに上下に小さく運動する。自分から遠ざかっていく人の上半身に注目すると、頭・胴体・腰が滑らかに連動しながら上下に動いているのが分かる。上下の動きは \(1\) センチか \(2\) センチ程度で大きくはないものの、人間の歩行が発する加速度信号の中で最も明確で、最も一貫していて、最も認識しやすい部分の一つである。

人間は歩行するとき一歩ごとに垂直方向に運動する。歩いているのが地球 (あるいは宇宙空間に浮かぶ巨大な球体) の上なら、この方向は都合のいいことに重力の方向と一致する。

私たちは加速度計を使って上下運動の回数を測定し、そこから歩数を計算する。スマートフォンは任意の方向に回転している可能性があるので、重力を利用して「下」の方向を判定する。つまり、歩数計は重力方向の上下運動の回数を数えることで歩数を測定する。

加速度計の付いたスマートフォンを上着またはズボンのポケットに入れて歩く人間の模式図を図 2 に示す。

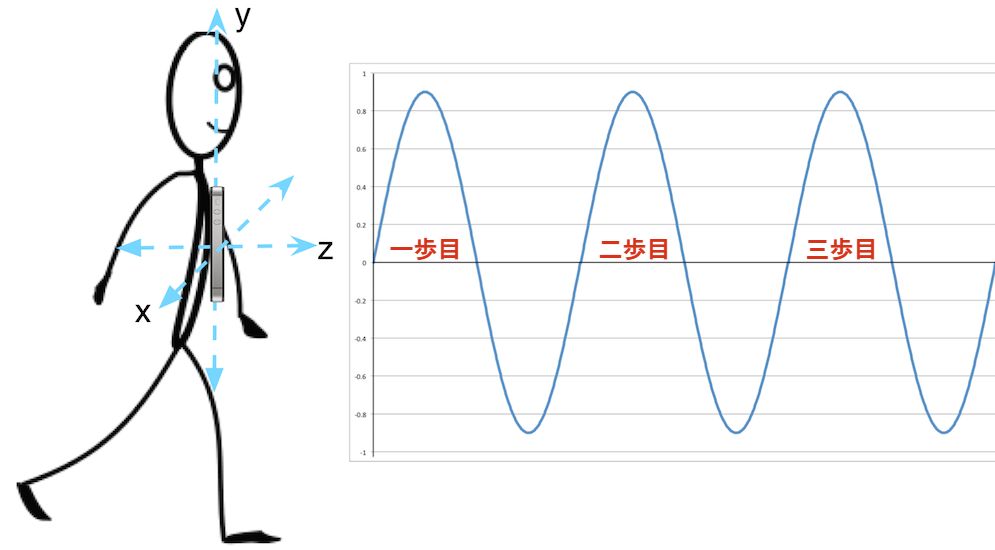
簡単のため、この人物に関して次の仮定をする:

\(z\) 軸方向に歩いている。
一歩ごとに \(y\) 軸方向に上下に動く。
歩いている間にスマートフォンの回転方向は変わらない。

私たちが仮定する完璧な世界では、歩行による上下の加速度は \(y\) 方向の完全なサイン波を描く。このサイン波の一周期がちょうど一歩に対応するので、歩数を測定するには加速度の最大値を検出すればよい。

あぁ、文章中にしか存在しない完璧な世界の何と美しいことか。問題はすぐに複雑そして興味深くなるので心配しないでほしい。私たちの世界に一匙の現実性を加えてみよう。

完璧な世界にも重力はある

重力は物体に作用し、特定の方向に加速度を生じさせる。この加速度を重力加速度 (gravitational acceleration) と呼ぶ。重力加速度が特殊な理由として、必ず存在すること、そして (本章の範囲では) \(9.8~\mathrm{m/s^2}\) で一定なことがある。

スマートフォンが画面を上にして置かれていると想像してほしい。本章で利用する座標系において、このスマートフォンは \(z\) の負方向に重力を受けている。重力によってスマートフォンは \(z\) の負方向に引っ張られるので、そこに搭載された加速度計は完全に静止した状態でも \(z\) 方向に \(-9.8~\mathrm{m/s^2}\) の加速度を記録する。この設定で加速度計から得られるデータを図 3 に示す。

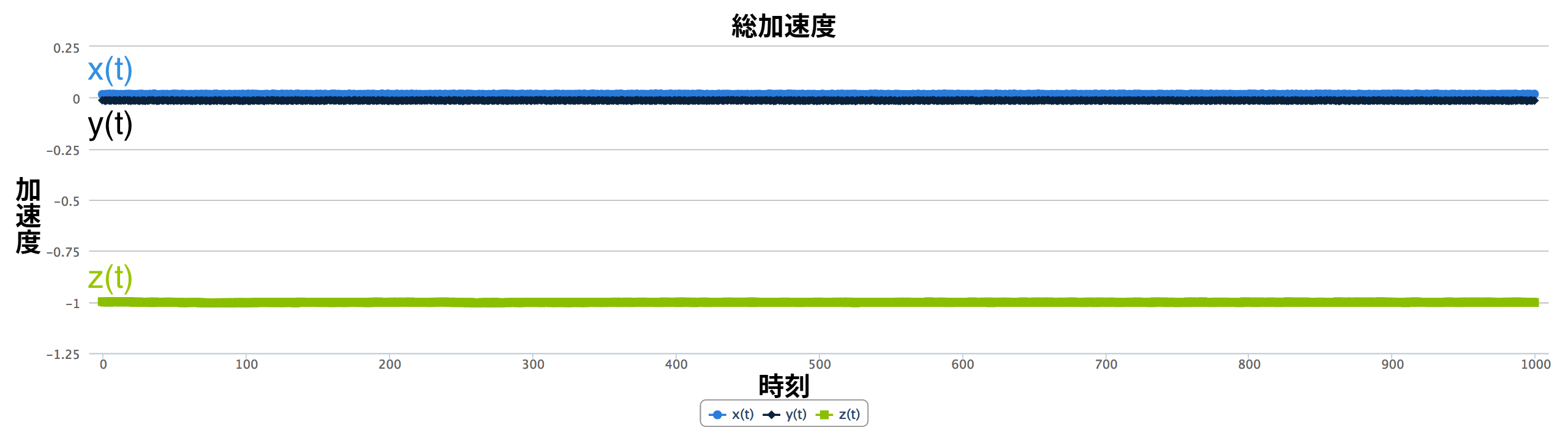
図 3. 静止している加速度計から得られるデータの例 — 図 3静止している加速度計から得られるデータの例

\(x(t)\) と \(y(t)\) は \(0\) で一定なのに対して、 \(z(t)\) は \(-g\) で一定なことに注目してほしい。私たちが考える加速度計は重力加速度を含んだ全ての加速度を記録する。

加速度計から得られる三つの時系列はそれぞれ各方向の総加速度 (total acceleration) を表す。総加速度はユーザー加速度 (user acceleration) と重力加速度 (gravitational acceleration) の和である。

ユーザー加速度とはユーザーの動きで生じたデバイスの加速度であり、デバイスが静止中は \(0\) となる。一方、ユーザーがデバイスを身に着けて移動しているときユーザー加速度が \(0\) になることはまずない。一定の速度を保ったまま移動するのは人間には難しいためである。

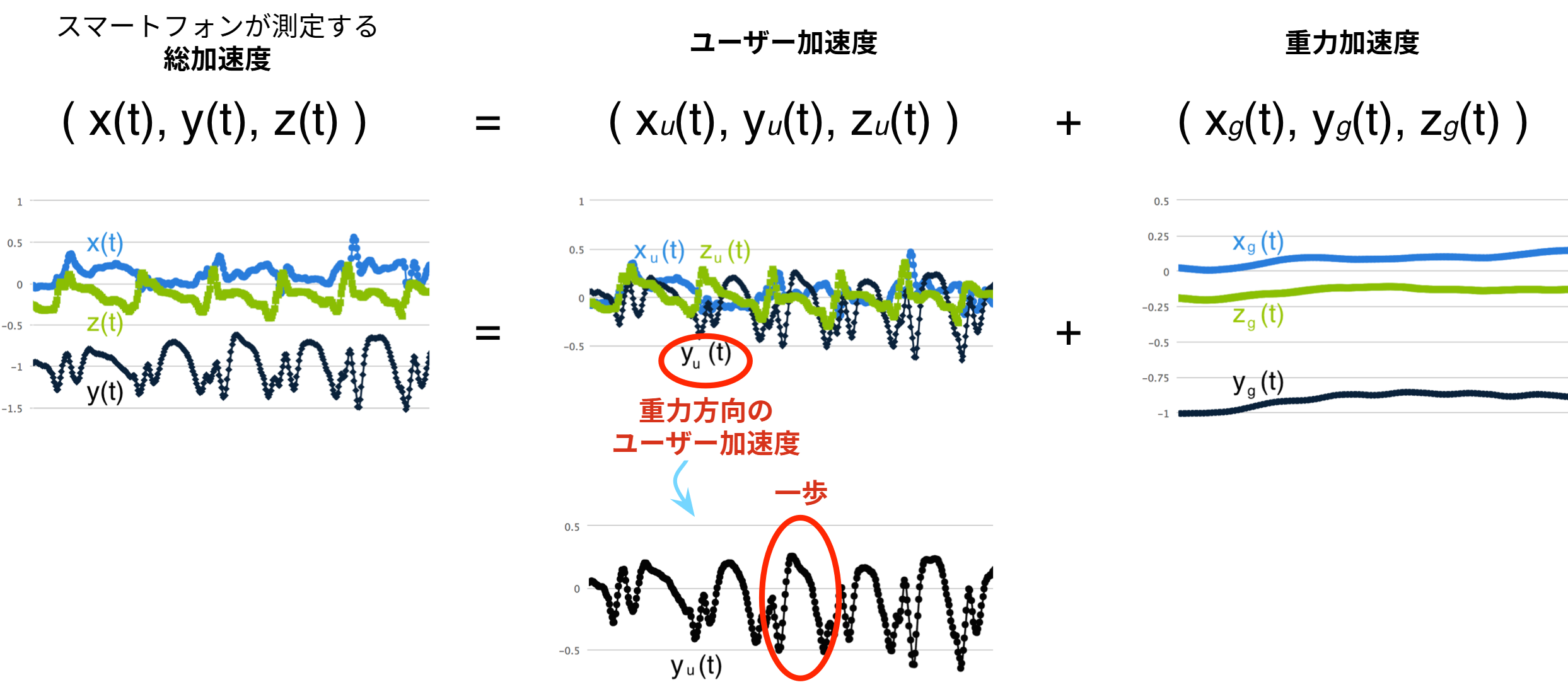
歩数を測定するには、ユーザーの移動が原因で生じる重力方向の加速度に注目する必要がある。そのため、加速度計から得られる三次元の加速度信号 (図 4) から重力方向のユーザー加速度を集めた時系列を抽出しなければならない。

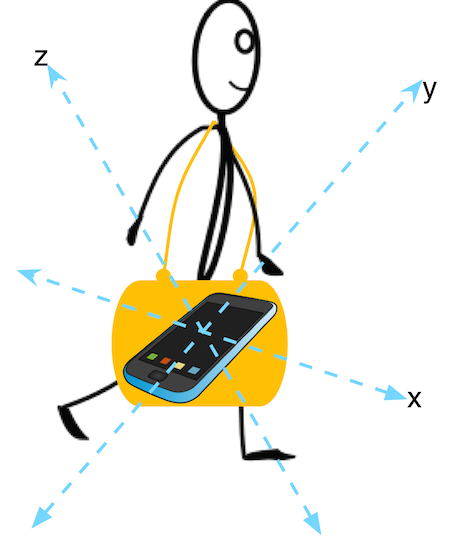
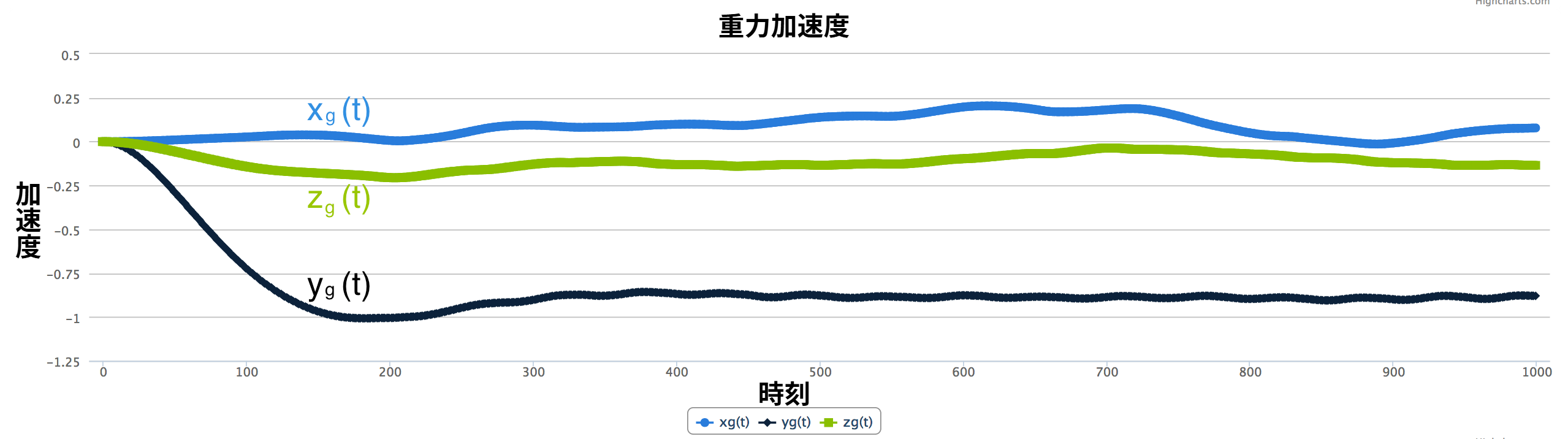
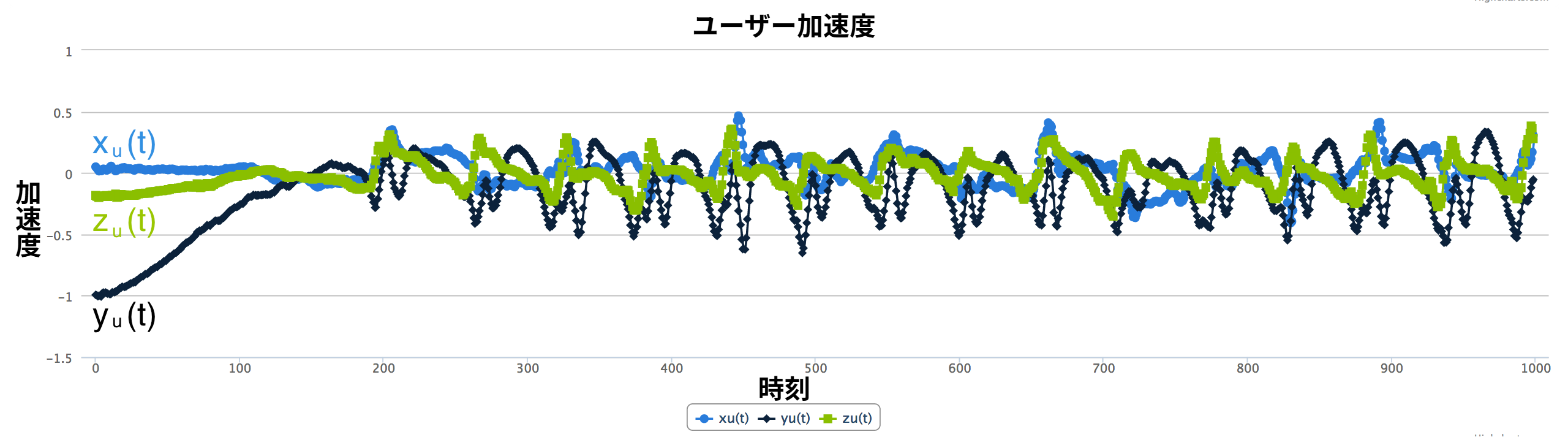
今考えている単純な例では、重力加速度の \(x(t)\) と \(z(t)\) は \(0\) で一定、\(y(t)\) は \(-g\) で一定となる。そのため総加速度のプロットで \(x(t)\) と \(z(t)\) は \(0\) の周辺を上下し、\(y(t)\) は \(-g\) の周辺を上下する。ユーザー加速度のプロットを見ると ── ユーザー加速度とは総加速度から重力加速度を引いた結果なので ── 三つある全ての時系列が \(0\) の周辺を上下しているのが分かる。\(y_{u}(t)\) が明らかなピークを持つことに注目してほしい。これは歩行によって生じた加速度の変化に対応する。重力加速度のプロットを見ると、\(y_{g}(t)\) は \(-g\) でほぼ一定、\(x_{g}(t)\) と \(z_{g}(t)\) は \(0\) でほぼ一定だと分かる。

よって、この例で重力方向のユーザー加速度を表す一次元の時系列 (歩数の測定に必要なデータ) は \(y_{u}(t)\) である。\(y_{u}(t)\) は完璧なサイン波ほどは滑らかでないものの、ピークは見つけられるので歩数は測定できる。ここまでは何も問題ない。では、私たちの世界に現実性をさらに加えてみよう。

人間は複雑な動物である

図 5 のようにスマートフォンが肩掛けのカバンの中に傾いたまま入っていたら、どうすればいいだろうか？さらに悪いことに、歩いている間にカバンの中でスマートフォンが回転したら？

なんてこった。この状況では \(x\), \(y\), \(z\) 方向全てにゼロでない重力加速度が加わるので、重力方向のユーザー加速度は三つの時系列を使わないと抽出できない。重力の作用している方向を求める必要もある。このためには、各方向の総加速度をユーザー加速度と重力加速度に分割しなければならない (図 6)。

こうすれば総加速度に含まれる重力方向のユーザー加速度成分を \(x\), \(y\), \(z\) 方向ごとに抽出できるので、それらを足せば重力方向のユーザー加速度が得られる。

この処理を次の二つのステップを使って定義する:

総加速度をユーザー加速度と重力加速度に分割する。
ユーザー加速度から重量方向の成分を抽出する。

それぞれのステップごとに見ていく。これからしばらくは数学者の帽子をかぶってほしい。

1. 総加速度をユーザー加速度と重力加速度に分割する

フィルタ (filter) と呼ばれるツールを使うと、総加速度の時系列をユーザー加速度の時系列と重力加速度の時系列に分割できる。

ローパスフィルタとハイパスフィルタ

フィルタとは信号処理で使われるツールであり、信号から不要な成分を取り除くために利用される。

ローパスフィルタ (low-pass filter) は低周波数の信号を通過させ、設定された閾値より高い周波数を持つ信号を減衰させる。逆に、ハイパスフィルタ (high-pass filter) は高周波数の信号を通過させ、設定された閾値より低い周波数を持つ信号を減衰させる。音楽に例えると、ローパスフィルタは高音域 (トレブル) を除去し、ハイパスフィルタは低音域 (バス) を除去する。

私たちの考えている問題では、周波数 (単位は Hz) は加速度がどれだけ速く変動するかを表す。例えば、一定の加速度は周波数 0 Hz を持ち、定数でない加速度は正の周波数を持つ。これは、定数である重力加速度は 0 Hz の信号であり、定数でないユーザー加速度は 0 Hz でない信号であることを意味する。

よって、総加速度をローパスフィルタに通せば重力加速度だけが残る。そして総加速度から重力加速度を引けばユーザー加速度が得られる。この操作は \(x\), \(y\), \(z\) 方向のそれぞれに対して実行できる (図 7)。

フィルタには様々な種類がある。これから使うフィルタは IIR (infinite impulse response, 無限インパルス応答) フィルタと呼ばれる。IIR フィルタを使うのは、実装が簡単で、オーバーヘッドも小さいためである。IIR フィルタの実装で使う式を次に示す:

\[ \begin{aligned} \text{output}_{i} = \alpha_{0}(&\text{input}_{i}\beta_{0} + \text{input}_{i-1}\beta_{1} + \text{input}_{i-2}\beta_{2} \\ & \ - \text{output}_{i-1}\alpha_{1} - \text{output}_{i-2}\alpha_{2}) \end{aligned} \]

デジタルフィルタの設計理論は本章の範囲を超えるが、ここで簡単に紹介する。広く研究されてきた魅力的な分野であるデジタルフィルタの設計理論は、数多くの実用的な応用を持つ。デジタルフィルタは任意の周波数または周波数の範囲を除去するように設計できる。上式中の \(\alpha\) と \(\beta\) は係数であり、カットオフ周波数や保持したい周波数の範囲に応じて設定される。

私たちは定数の重力加速度を除いた全ての周波数を除去したいので、0.2 Hz より高い周波数を減衰させるようにフィルタの係数を設定する。閾値を 0 Hz より少しだけ大きくしている点に注目してほしい。重力が生成するのは 0 Hz の加速度であるものの、完璧でない世界に存在する現実の加速度計もまた完璧ではないので、測定で生じる誤差を吸収できるようにフィルタを設定する必要がある。

ローパスフィルタの実装

先述の例を使ってローパスフィルタの実装を見ていこう。このフィルタは、各成分を次のように分割する:

\(x(t)\) を \(x_{g}(t)\) と \(x_{u}(t)\) に分割する。
\(y(t)\) を \(y_{g}(t)\) と \(y_{u}(t)\) に分割する。
\(z(t)\) を \(z_{g}(t)\) と \(z_{u}(t)\) に分割する。

まず、上に示したフィルタの式を適用できるように重力加速度の最初の二つの値を \(0\) に初期化する。:

\[ x_{g}(0) = x_{g}(1) = y_{g}(0) = y_{g}(1) = z_{g}(0) = z_{g}(1) = 0 \]

続いてフィルタの式をそれぞれの時系列に適用する:

\[ \begin{aligned} y_{g}(t) &= \alpha_{0}(y(t)\beta_{0} + y(t-1)\beta_{1} + y(t-2)\beta_{2} - y_{g}(t-1)\alpha_{1} - y_{g}(t-2)\alpha_{2}) \\ x_{g}(t) &= \alpha_{0}(x(t)\beta_{0} + x(t-1)\beta_{1} + x(t-2)\beta_{2} - x_{g}(t-1)\alpha_{1} - x_{g}(t-2)\alpha_{2}) \\ z_{g}(t) &= \alpha_{0}(z(t)\beta_{0} + z(t-1)\beta_{1} + z(t-2)\beta_{2} - z_{g}(t-1)\alpha_{1} - z_{g}(t-2)\alpha_{2}) \end{aligned} \]

これらの式を使って計算したローパスフィルタ後の時系列を図 8 に示す。

図 8. ローパスフィルタによって抽出された重力加速度 — 図 8ローパスフィルタによって抽出された重力加速度

\(x_{g}(t)\) と \(z_{g}(t)\) は \(0\) の周辺を上下し、\(g_{g}(t)\) はすぐに \(-g\) まで減少する。\(y_{g}(t)\) の値が最初 \(0\) なのは、初期値を \(0\) に設定したためである。

続いて、ユーザー加速度を求めるために、総加速度から重力加速度を引く:

\[ \begin{aligned} x_{u}(t) &= x(t) - x_{g}(t) \\ y_{u}(t) &= y(t) - y_{g}(t) \\ z_{u}(t) &= z(t) - z_{g}(t) \end{aligned} \]

この結果を図 9 に示す。これで総加速度をユーザー加速度と重力加速度に分割することに成功した！

2. 重力方向のユーザー加速度を抽出する

\(x_{u}(t)\), \(y_{u}(t)\), \(z_{u}(t)\) にはユーザーの動きによって生じた全ての加速度が含まれているのに対して、歩数を測定する上で重要なのは重力方向のユーザー加速度である。よって次は重力方向のユーザー加速度からなる一次元の時系列を手にすることが目標となる。この加速度は各方向のユーザー加速度から計算される。

この問題に取り掛かるために、簡単な線形代数を復習する。数学者の帽子はかぶったままで！

内積

座標について勉強すると、すぐに内積に出会うことになる。内積 (dot product) は \(x\), \(y\), \(z\) 座標の大きさと向きを比較するための基礎的なツールの一つである。

内積を使うと三次元空間から一次元空間にデータを移すことができる。具体的には、ユーザー加速度と重力加速度という二つの三次元時系列の内積を取ると、重力方向のユーザー加速度成分を表す一次元の時系列が得られる (図 10)。この時系列をこれから \(a(t)\) と呼ぶ。重要な時系列には名前を付与えてしかるべきだからである。

内積の実装

これまで定義してきた時系列に内積の定義を適用すれば \(a(t) = x_{u}(t)x_{g}(t) + y_{u}(t)y_{g}(t) + z_{u}(t)z_{g}(t)\) を得る。先述の通り、内積の結果 \(a(t)\) は一次元の時系列である (図 11)。

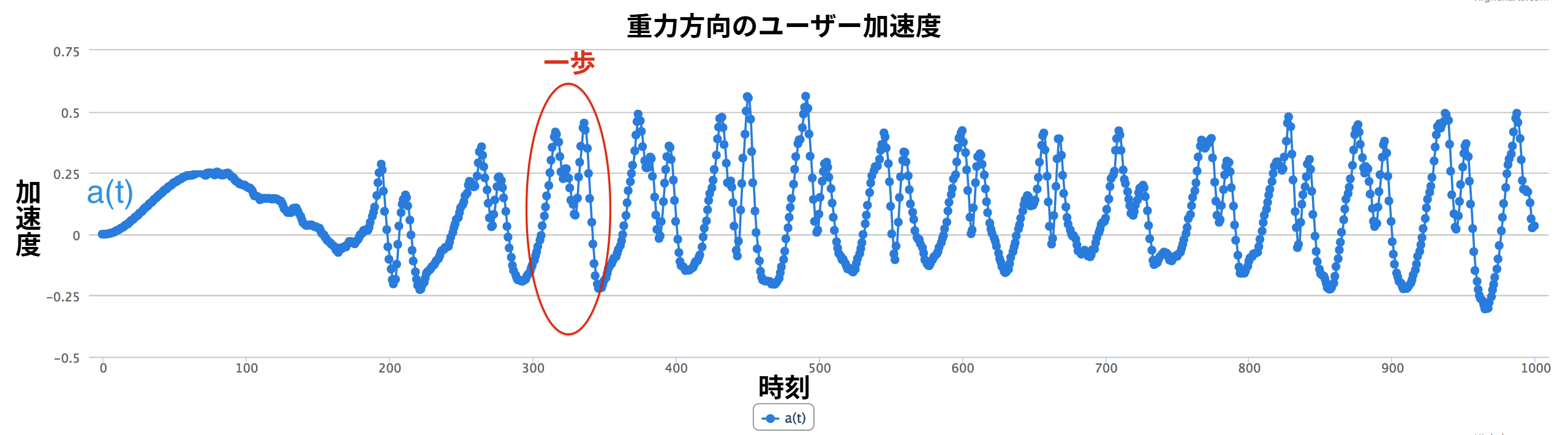
図 11. 内積の結果 {{}}a(t){{}} — 図 11内積の結果 \(a(t)\)

\(a(t)\) のプロットを見ると歩行の様子が大まかに見て取れる。内積は非常に強力でありながら美しく単純なツールである。

現実世界における解決法

一見すると単純な問題であっても、現実の世界と現実の人間が持つ厄介な特徴を考えに入れていくと複雑になることを見た。その結果、私たちは歩数の計測にかなり近づき、理想的なサイン波にいくらか似た形をした \(a(t)\) を手に入れることができた。ただ、その形はサイン波に「なんとなく」似ているだけに過ぎないので、ガタガタの時系列 \(a(t)\) をどうにかして滑らかにする必要がある。現在の \(a(t)\) が持つ四つの主要な問題を図 12 に示す。一つずつ見ていこう。

図 12. 無視すべきピーク: 短い・長い・低い・ギリギリ — 図 12無視すべきピーク: 短い・長い・低い・ギリギリ

1. 短いピーク

歩いたときスマートフォンが揺れ動くと加速度の時系列に高周波成分が加わり、 \(a(t)\) に短い「ジャンプ」が加わる。このジャンプはノイズとも呼ばれる。多くのデータセットを調べることで、歩行の加速度は最大でも 5 Hz だと分かったとしよう。このときローパス IIR フィルタの \(\alpha\) と \(\beta\) を調整して 5 Hz より周波数が高い成分を減衰させることでノイズを除去できる。

2. 長いピーク

サンプリングレートが 100 のとき、図 12 の左から二番目のプロットに示されたピークは 1.5 秒にわたっているので、歩行によるものと判断するべきではない。多くのデータセットを調べることで、どんなに遅い歩行でも 1 Hz より高い周波数を持つと分かったとする。ここでも、ハイパス IIR フィルタの \(\alpha\) と \(\beta\) を調整して 1 Hz より周波数が低い成分を減衰させることで長いピークを除去できる。

3. 低いピーク

ユーザーがスマートフォンのアプリを使っていたり通話していたりすると、加速度計は重力方向に小さな動きを記録し、時系列上に低いピークが現れる。こういった低いピークを除去するには、\(a(t)\) が事前に設定した閾値を下から上に通り過ぎたときにだけピークを検出するようにすればよい。

4. ギリギリのピーク

多くのユーザーの異なる歩行に対応するために、様々な歩行サンプルから導いた歩行周波数の最小値と最大値を設定すると説明した。これは、周波数が少しだけ低かったり、少しだけ高かったりするために歩行とみなされないピークが存在することを意味する。上述した三つのテクニックを適用すれば多くの場合で滑らかなピークが得られるものの、ときには図 12 の左から四つ目のプロットのように「ギリギリ」のピークが得られる可能性がある。

こういったピークがあると、一つのピークを複数の歩数と誤認する可能性がある。この問題を解決するために、ヒステリシス (hysteresis) と呼ばれる手法を用いる。ヒステリシスとは、出力を過去の入力に依存させることを言う。具体的には、閾値を下から上に通り過ぎることに加えて、\(0\) を上から下に通り過ぎることを歩数を検知する条件とする。こうすると加速度が十分に低くなった後に閾値より大きくなったピークだけが歩数と認識されるので、歩数を正しく測定できる。

とっっっても綺麗なピーク

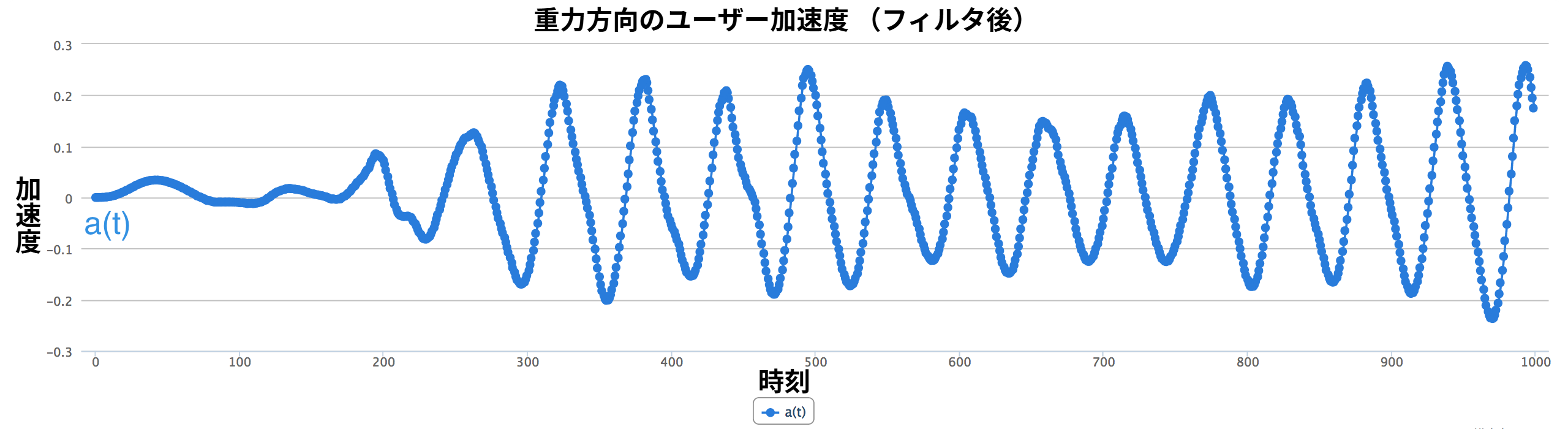
以上の四つのシナリオに対処すると、ガタガタだった \(a(t)\) が理想的なサイン波にかなり近づく (図 13)。ここまでくれば、歩数の測定が可能になる。

まとめ

歩数を測定する問題は一見すると簡単に見えたものの、現実の世界と現実の人間を考えに入れると厄介な問題が現れた。この問題をどのように解決したかを振り返ろう:

最初に与えられる総加速度 \((x(t), y(t), z(t))\) だった。
ローパスフィルタを使って総加速度をユーザー加速度 \((x_{u}(t), y_{u}(t), z_{u}(t))\) と重力加速度 \((x_{g}(t), y_{g}(t), z_{g}(t))\) に分割した。
\((x_{u}(t), y_{u}(t), z_{u}(t))\) と \((x_{g}(t), y_{g}(t), z_{g}(t))\) の内積を取り、重力方向のユーザー加速度 \(a(t)\) を得た。
もう一度ローパスフィルタを使って、\(a(t)\) に含まれる高周波成分 (ノイズ) を除去した。
ハイパスフィルタを使って \(a(t)\) に含まれる低周波成分を除去し、長いピークを取り除いた。
低いピークを無視するための閾値を設定した。
ヒステリシスを利用してギリギリのピークを複数の歩数と誤認することを防いだ。

ソフトウェア開発者は初学者のときまたはアカデミアで活動していたとき、与えられた完璧な信号に対して歩数を測定するコードを書くことを求められたかもしれない。それ自体は興味深いコーディング課題ではあるものの、現実の問題には適用できない。これまでに見てきたように、現実では重力と人間によって問題がさらに複雑になる。私たちは数学的ツールを使って複雑性に対処し、現実世界の問題を解くことができた。続いて、この解決法をコードに変換しよう。

コードの解説

本章の目標は加速度計から得られたデータを受け取り、データをパース・処理・解析し、歩数・歩行距離・歩行時間を返すウェブアプリケーションを Ruby で作成することである。

準備

私たちが利用する解決法では、時系列に対してフィルタを適用する場面が何度かある。フィルタのコードをプログラムのそこら中に分けて書くよりは、フィルタ処理を担当するクラスを作成するのが望ましい。そうすればフィルタを改善・調整する場合に変更が必要になるのは一つのクラスだけとなる。この戦略は関心の分離 (separation of concerns) と呼ばれる。主要な関心を一つだけ持った部分にプログラムを切り分けることを奨励する設計原則であり、整理された管理可能なコードを拡張な可能な形で書くための美しい手法である。本章では関心の分離に何度か触れる。

フィルタ処理を実装するクラスのコードを次に示す。クラスの名前はもちろん Filter である:

class Filter

  COEFFICIENTS_LOW_0_HZ = {
    alpha: [1, -1.979133761292768, 0.979521463540373],
    beta:  [0.000086384997973502, 0.000172769995947004, 0.000086384997973502]
  }
  COEFFICIENTS_LOW_5_HZ = {
    alpha: [1, -1.80898117793047, 0.827224480562408],
    beta:  [0.095465967120306, -0.172688631608676, 0.095465967120306]
  }
  COEFFICIENTS_HIGH_1_HZ = {
    alpha: [1, -1.905384612118461, 0.910092542787947],
    beta:  [0.953986986993339, -1.907503180919730, 0.953986986993339]
  }

  def self.low_0_hz(data)
    filter(data, COEFFICIENTS_LOW_0_HZ)
  end

  def self.low_5_hz(data)
    filter(data, COEFFICIENTS_LOW_5_HZ)
  end

  def self.high_1_hz(data)
    filter(data, COEFFICIENTS_HIGH_1_HZ)
  end

private

  def self.filter(data, coefficients)
    filtered_data = [0,0]
    (2..data.length-1).each do |i|
      filtered_data << coefficients[:alpha][0] *
                      (data[i]            * coefficients[:beta][0] +
                       data[i-1]          * coefficients[:beta][1] +
                       data[i-2]          * coefficients[:beta][2] -
                       filtered_data[i-1] * coefficients[:alpha][1] -
                       filtered_data[i-2] * coefficients[:alpha][2])
    end
    filtered_data
  end

end

時系列をフィルタするときは、Filter が持つクラスメソッドのいずれかにフィルタ対象のデータを渡して呼び出す:

low_0_hz は 0 Hz 付近の周波数だけを通過させるローパスフィルタを適用する。
low_5_hz は 5 Hz 以下の周波数だけを通過させるローパスフィルタを適用する。
high_1_hz は 1 Hz 以上の周波数だけを通過させるハイパスフィルタを適用する。

これらのクラスメソッドはどれも IIR フィルタを実行して結果を返す filter メソッドを呼び出す。将来フィルタを追加することになったとしても、Filter クラスを変更するだけで対応できる。コードの可読性を上げるためにマジックナンバーはクラスの最初で定義されることに注目してほしい。

入力フォーマット

入力データは Android スマートフォンや iPhone といったモバイル機器から取得される。現在販売されているスマートフォンの多くは加速度計を搭載しており、総加速度を測定できる。総加速度が記録された入力データフォーマットをここでは混合フォーマット (combined format) と呼ぶ。全てではないものの、多くの機器はユーザー加速度と重力加速度を別々に記録できる。そういったフォーマットを分離フォーマット (separated format) と呼ぶ。分離フォーマットのデータを返せる機器は必ず混合フォーマットでもデータを返せる。一方で、逆は成り立たないこともある: 一部の機器は混合フォーマットでしか加速度を記録できない。入力データが混合フォーマットの場合は、ローパスフィルタを適用して分離フォーマットに変換する必要がある。

加速度計を持った全てのモバイル機器に対応したいので、両方のフォーマットを扱えなければならない。それぞれのフォーマットを順に見ていこう。

混合フォーマット

混合フォーマットに含まれるデータは \(x\), \(y\), \(z\) 方向の総加速度を収めた時系列である。\(x\), \(y\), \(z\) 方向の値はコンマで区切られ、単位時間ごとのサンプルはセミコロンで区切られる:

\[ x_1,y_1,z_1;\ \ldots\ x_n,y_n,z_n; \]

分離フォーマット

分離フォーマットに含まれるデータは \(x\), \(y\), \(z\) 方向のユーザー加速度と重力加速度を収めた時系列である。二つの値の間には垂直線の記号が書かれる:

\[ x^{u}_1,y^{u}_1,z^{u}_1 \vert x^{g}_1,y^{g}_1,z^{g}_1;\ \ldots\ x^{u}_n,y^{u}_n,z^{u}_n \vert x^{g}_n,y^{g}_n,z^{g}_n; \]

入力フォーマットが複数あるのに標準フォーマットがない

複数の入力フォーマットを扱うのはプログラミングでよくある問題である。プログラム全体を両方のフォーマットに対応させるには、全てのコードが二つのフォーマットの処理方法を知らなければならない。この方法だと、特に第三の (あるいは第四、第五、第百の) フォーマットが追加されたときに、コードが急速に複雑になる。

標準フォーマット

この問題に対処する最も綺麗な手法は、二つのフォーマットを受け取るようにしつつ、受け取ったデータを可能な限り早く標準フォーマットに変換することである。こうすれば、プログラムの他の部分は標準フォーマットだけを扱うだけで済む。私たちが利用する解決法はユーザー加速度と重力加速度を分離して扱うので、加速度を分離した後のデータを標準フォーマットとする必要がある (図 14)。

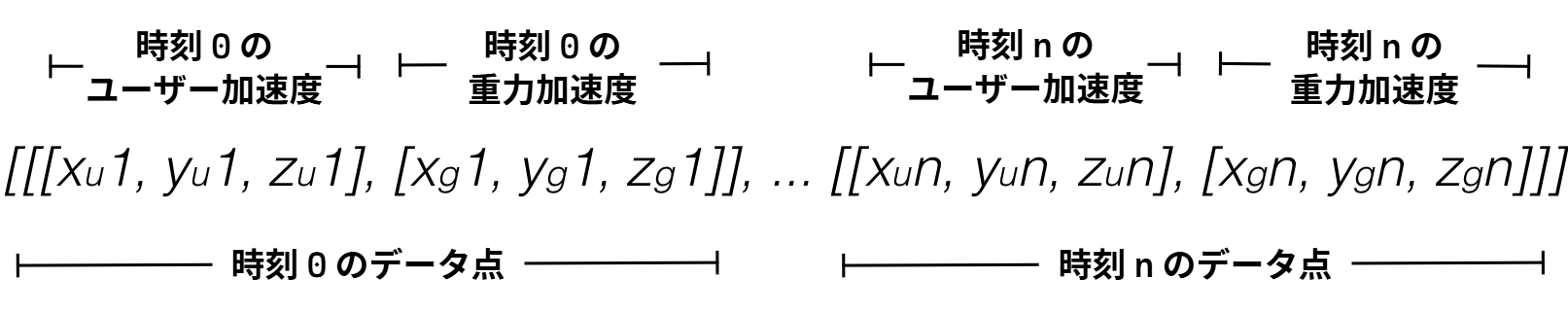
この標準フォーマットは時系列を格納し、各データ点は特定の時刻における加速度を表す。このフォーマットは配列の配列の配列を利用する。一枚ずつ皮を剥いていこう:

一つ目の (最も外側の) 配列は単に全てのデータを保持するために存在する。
一つ目の配列はデータサンプルごとに一つの配列を要素に持つ。もしサンプリングレートが 100 で 10 秒間にわたってデータを収集したなら、一つ目の配列には 1000 個の配列が含まれる。
二つ目の配列には二つの配列が含まれる。この二つの配列はいずれも \(x\), \(y\), \(z\) 方向の加速度を表す。一つ目の配列はユーザー加速度を、二つ目の配列は重力加速度を表す。

パイプライン

システムに対する入力は加速度計から得られたデータ、歩いているユーザーに関する情報 (性別や歩幅など)、そして歩行試行に関するデータ (サンプルレートや実際の歩数など) である。システムは信号処理を使った解決法を適用し、計算された歩数、実際の歩数と計算された歩数の差、歩行距離、経過時間を出力する。入力から出力までのプロセス全体を図 15 に示す。

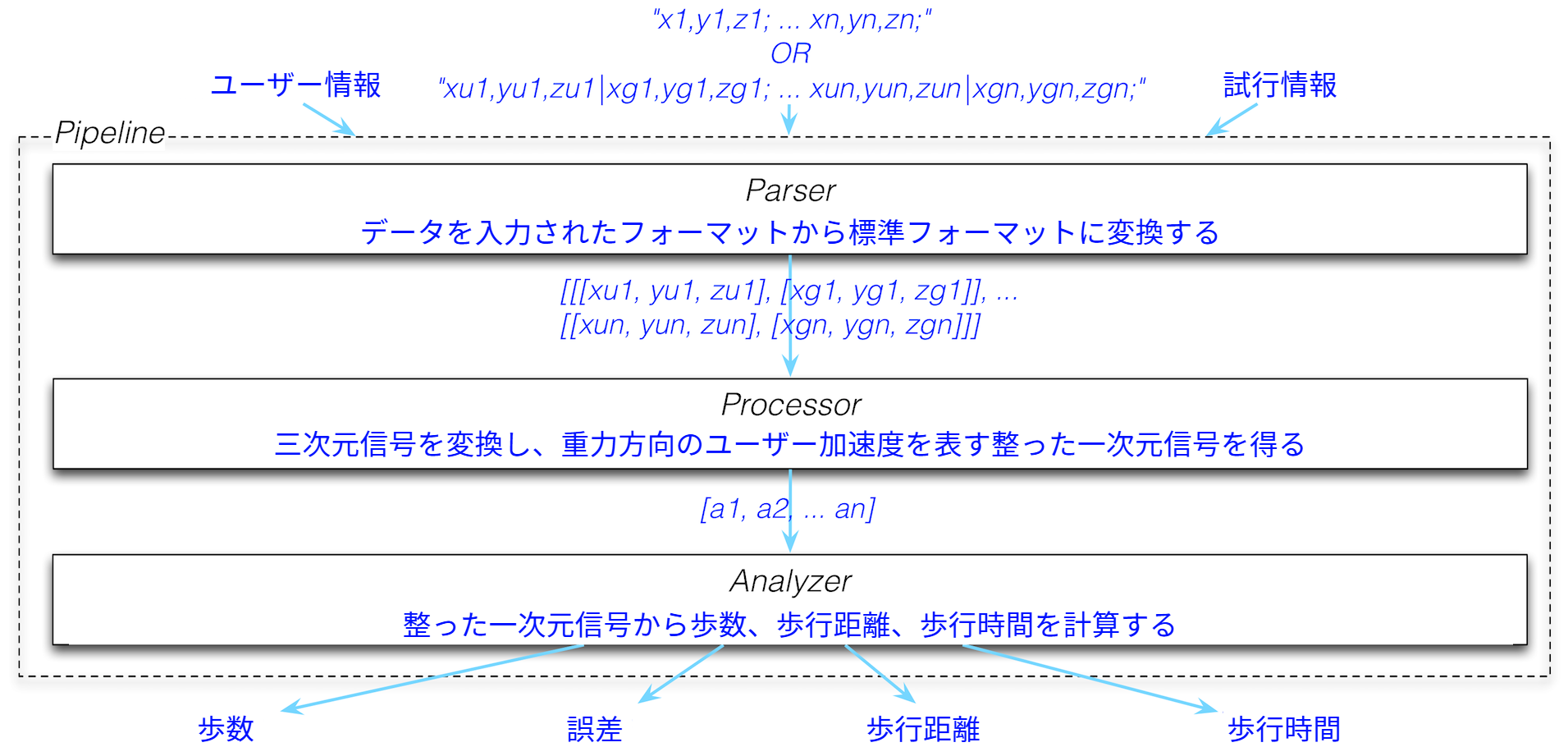
関心の分離の考え方に従って、パイプラインの各構成要素 ── パース・データ処理・解析 ── に対応するコードを一つずつ書いていく。

パース

データは可能な限り早い段階で標準フォーマットに変換するのが望ましい。そのため、既知の二つのフォーマットを受け取って標準フォーマットに変換するパーサーをパイプラインの最初の構成要素とするのが理にかなっている。標準フォーマットはユーザー加速度と重力加速度を分割した形式なので、パーサーが混合フォーマットのデータを受け取ったときはローパスフィルタを使ったデータの変換が必要になる。

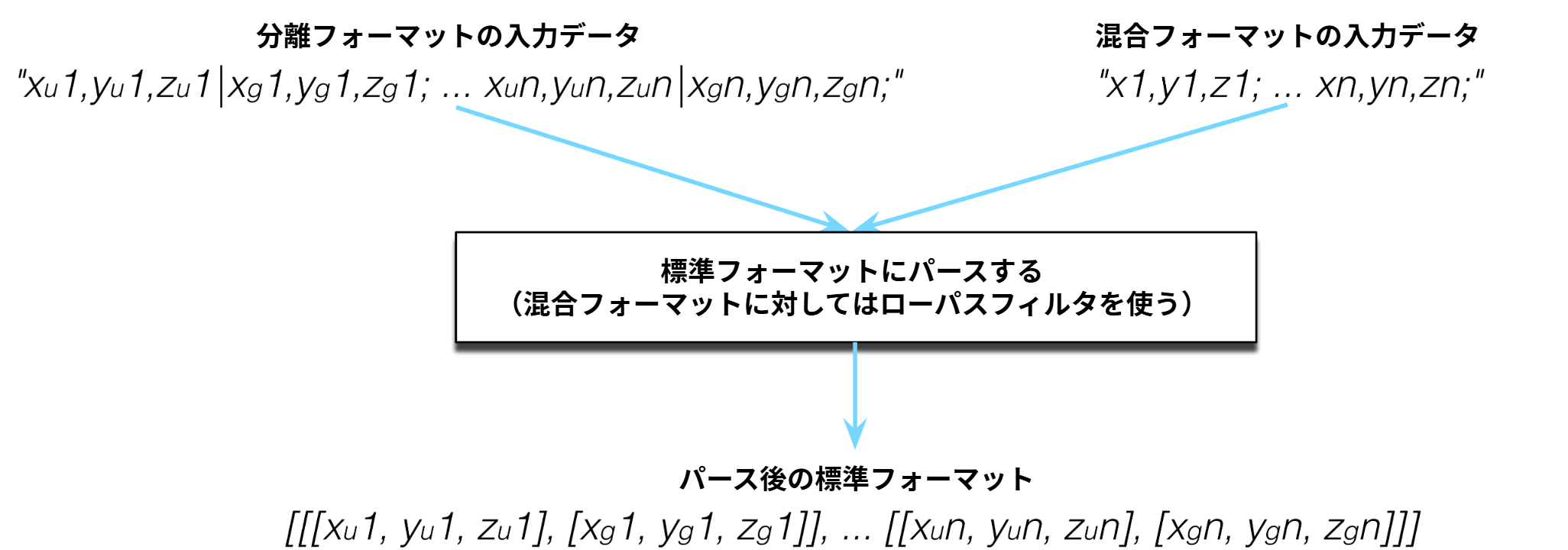
将来、異なる入力フォーマットを追加する必要が生じたとしても、変更が必要になるのはパーサーだけとなる。関心の分離を意識して、パース処理を担当する Parser クラスを作成しよう:

class Parser

  attr_reader :parsed_data

  def self.run(data)
    parser = Parser.new(data)
    parser.parse
    parser
  end

  def initialize(data)
    @data = data
  end

  def parse
    @parsed_data = @data.to_s.split(';').map { |x| x.split('|') }
                   .map { |x| x.map { |x| x.split(',').map(&:to_f) } }

    unless @parsed_data.map { |x| x.map(&:length).uniq }.uniq == [[3]]
      raise 'Bad Input. Ensure data is properly formatted.'
    end

    if @parsed_data.first.count == 1
      filtered_accl = @parsed_data.map(&:flatten).transpose.map do |total_accl|
        grav = Filter.low_0_hz(total_accl)
        user = total_accl.zip(grav).map { |a, b| a - b }
        [user, grav]
      end

      @parsed_data = @parsed_data.length.times.map do |i|
        user = filtered_accl.map(&:first).map { |elem| elem[i] }
        grav = filtered_accl.map(&:last).map { |elem| elem[i] }
        [user, grav]
      end
    end
  end

end

Parser クラスは初期化メソッド initialize とクラスレベルの run メソッドを持つ。これは今後も何度か出てくるパターンなので、ここで議論しておくに値する。一般に initialize はオブジェクトの初期化を行うメソッドであり、多くの処理をすべきではない。Parser の initialize メソッドは受け取った data (混合フォーマットまたは分離フォーマット) をインスタンス変数 @data に保存するだけの処理しかしない。インスタンスメソッド parse は @data のパースという大掛かりな処理を実行し、標準フォーマットの結果を @parsed_data に格納する。このとき、他の部分のコードは Parse を使うとき必ず parse を呼び出す。そこで、Paser クラスのインスタンスを作成し、その parse メソッドを呼び出し、最終的なインスタンスを返すクラスレベルの run メソッドを作成する。こうしておけば、入力データを run に渡すだけで @parsed_data が適切に設定された Parser のインスタンスを取得できる。

実際のパース処理を実行する parse メソッドを見ていこう。最初のステップとして、文字列データが数値データに変換される。以前に見たように、この結果は配列の配列の配列のはずである。続いて、正しいフォーマットのデータが入力されたことを確認する。最も内側の配列の要素数が全て 3 でなければ例外を送出する。そうでなければ次のステップに進む。

この時点における @parsed_data の形状は入力のフォーマットによって異なる点に注意してほしい。入力が混合フォーマットの場合、@parsed_data の各要素は一つの配列からなる配列となる:

\[ [[[x_1, y_1, z_1]], \ldots [[x_n, y_n, z_n]]] \]

一方、入力が分離フォーマットの場合、@parsed_data の各要素は二つの配列からなる配列となる:

\[ [[[x_{1}^{u},y_{1}^{u},z_{1}^{u}], [x_{1}^{g},y_{1}^{g},z_{1}^{g}]], ... [[x_{n}^{u},y_{n}^{u},z_{n}^{u}], [x_{n}^{g},y_{n}^{g},z_{n}^{g}]]] \]

この操作が終わったとき、分離フォーマットの入力は最終的な標準フォーマットとなる。素晴らしい。しかし、入力が混合フォーマットのとき (つまり、分離フォーマットで二つの配列がある部分に一つの配列しかないとき) は、二つのループを実行する必要がある。一つ目のループは Filter.low_0_hz を使って総加速度をユーザー加速度と重力加速度に分割し、二つ目のループはデータを標準フォーマットに変形する。

parse を実行すると、標準フォーマットのデータが @parsed_data に格納される。このとき入力データが混合フォーマットか分離フォーマットかを気にする必要はない。一丁上がりだ！

プログラムを洗練させていくことになったら、例外に付けるエラーメッセージを詳細にして入力データの問題が簡単に分かるようにすることが改善点の一つとして考えられる。

データ処理

本章の前半で説明した方法で歩数を測定するには、データをパースした後に次のステップを踏む必要がある:

内積を使って重力方向のユーザー加速度を抽出する。
短い (高周波数の) ピークと長い (低周波数の) ピークをローパスフィルタとハイパスフィルタで除去する。
低いピークとギリギリのピークは歩数を測定するときのコードで回避する。

パースによって手に入る標準フォーマットのデータは、上記の処理によって歩数の測定に利用できる整ったデータに変換される (図 17)。

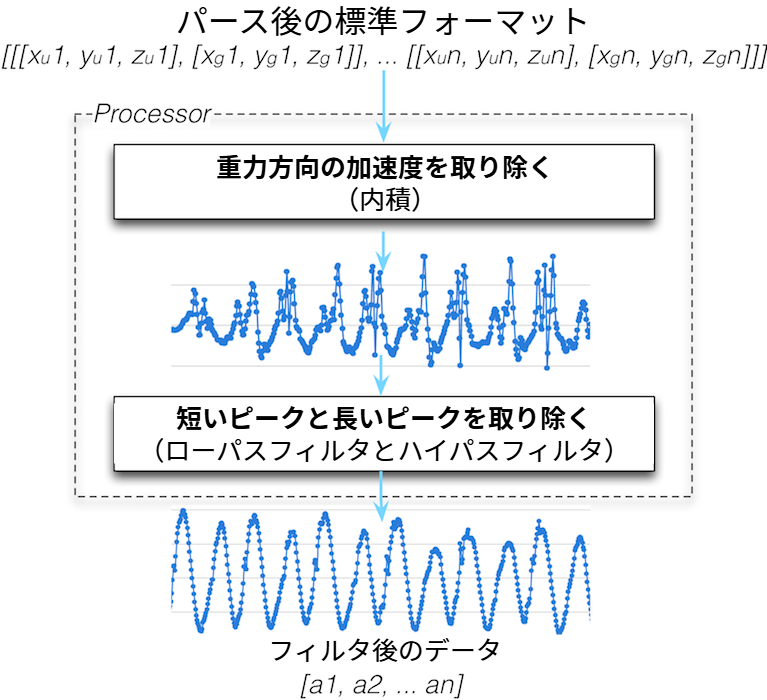
この処理の目的は、標準フォーマットのデータを少しずつ洗浄し、理想的なサイン波に可能な限り近づけることにある。上記の二つの操作 (内積とフィルタ) は大きく異なるものの、データを処理している点は共通しているので、Processor という一つのクラスに実装する。

class Processor

  attr_reader :dot_product_data, :filtered_data

  def self.run(data)
    processor = Processor.new(data)
    processor.dot_product
    processor.filter
    processor
  end

  def initialize(data)
    @data = data
  end

  def dot_product
    @dot_product_data = @data.map do |x|
      x[0][0] * x[1][0] + x[0][1] * x[1][1] + x[0][2] * x[1][2]
    end
  end

  def filter
    @filtered_data = Filter.low_5_hz(@dot_product_data)
    @filtered_data = Filter.high_1_hz(@filtered_data)
  end

end

ここでも run と initialize を使った Parser と同様のパターンが使われている。run は上述のデータ処理を実行するメソッド dot_product と filter を直接呼び出す。dot_product は内積を使って重力方向のユーザー加速度を抽出し、filter はローパスフィルタとハイパスフィルタを適用して短いピークと長いピークを取り除く。

歩数計の機能

歩数計を使用する人物に関する情報が与えられるなら、歩数以外の情報も測定できる。本プロジェクトで実装する歩数計は歩数の他に歩行距離と経過時間も測定する。

歩行距離

身に付けて使う歩数計は通常一人のユーザーによって使われる。歩行の間に移動した距離はユーザーの歩幅と歩数を乗じれば得られる。歩幅が分からない場合でも、性別や身長といった情報をユーザーから (拒否可能な形で) 集めれば推定ができる。こういった情報を格納する User クラスを作成しよう:

class User

  GENDER      = ['male', 'female']
  MULTIPLIERS = {'female' => 0.413, 'male' => 0.415}
  AVERAGES    = {'female' => 70.0,  'male' => 78.0}

  attr_reader :gender, :height, :stride

  def initialize(gender = nil, height = nil, stride = nil)
    @gender = gender.to_s.downcase unless gender.to_s.empty?
    @height = Float(height) unless height.to_s.empty?
    @stride = Float(stride) unless stride.to_s.empty?

    raise 'Invalid gender' if @gender && !GENDER.include?(@gender)
    raise 'Invalid height' if @height && (@height <= 0)
    raise 'Invalid stride' if @stride && (@stride <= 0)

    @stride ||= calculate_stride
  end

private

  def calculate_stride
    if gender && height
      MULTIPLIERS[@gender] * height
    elsif height
      height * (MULTIPLIERS.values.reduce(:+) / MULTIPLIERS.size)
    elsif gender
      AVERAGES[gender]
    else
      AVERAGES.values.reduce(:+) / AVERAGES.size
    end
  end

end

User クラスの先頭では、マジックナンバーや固定文字列がコード中に散乱するのを防ぐための定数が定義される。議論を簡単にするため、MULTIPLIERS と AVERAGES の値は多様な人々を対象とする大規模なサンプルから得られていると仮定する。

initialize メソッドは省略可能な引数として gender, height, stride を取る。これらの引数が与えられた場合は、簡単な整形を行った結果が同じ名前のインスタンス変数に格納される。引数の値が正当でない場合は例外を送出する。

省略可能引数が全て与えられた場合は、引数で指定された歩幅 stride が優先される。stride が与えられない場合は、calculate_stride メソッドがユーザーの歩幅の最も正確な推定値を計算する。このメソッドは if を使って次の処理を行う:

最も正確な計算方法は、ユーザーの身長に性別から求まる係数を乗じるものである。この方法は性別と身長が両方とも分かっているときにだけ利用できる。
身長は性別よりも優れた歩幅の指標なので、性別が与えられず身長だけが与えられた場合は身長に MULTIPLIERS の平均を乗じて推定値とする。
性別しか分からない場合は、AVERAGES に格納された性別ごとの平均の歩幅を推定値とする。
最後に、ユーザーに関する情報が何もない場合は AVERAGES の平均を推定値とする。

if 文を下るにしたがって歩幅の推定値が正確でなくなっていく点に注目してほしい。User クラスは可能な限り正確な歩幅の推定値を計算する。

経過時間

Processor の @parsed_data に含まれるデータサンプルの個数を加速度計のサンプリングレートで割れば経過時間が得られる。サンプリングレートはユーザーではなく歩行試行に関係する値なので、そして User クラスはサンプリングレートを利用しないので、ここで非常に小さな Trial クラスを作っておく:

class Trial

  attr_reader :name, :rate, :steps

  def initialize(name, rate = nil, steps = nil)
    @name  = name.to_s.delete(' ')
    @rate  = Integer(rate.to_s) unless rate.to_s.empty?
    @steps = Integer(steps.to_s) unless steps.to_s.empty?

    raise 'Invalid name'  if @name.empty?
    raise 'Invalid rate'  if @rate && (@rate <= 0)
    raise 'Invalid steps' if @steps && (@steps < 0)
  end

end

Trial の属性リーダーは initialize メソッドに渡された引数を使って設定される:

name は歩行試行の名前を表す。異なる試験を区別するために存在する。
rate は歩行試行で使用された加速度計のサンプリングレートを表す。
steps は実際の歩数を表す。正確な歩数と計算された歩数の差を計算するために存在する。

User クラスと同様に、一部の情報は省略できる。歩行試行に関する追加の情報が利用可能な場合は、それを Trial クラスに提供すれば経過時間などの追加の結果を得られる。また、正当でない値を受け取ったときに例外を送出する点も User クラスと同様である。

歩数の測定

いよいよ歩数を測定するコードを実装する。これまでに示してきた処理で Processor クラスの @filtered_data には重力方向のユーザー加速度の時系列を整形したものが格納されている。また、ユーザーと歩行試行を表すクラスも作成した。足りないのは User と Trial の情報を使って @filtered_data を解析し、歩数・歩行距離・経過時間を計算する処理である。

この解析処理は Processor が担当するデータ整形とは異なり、User と Trial が担当する情報収集・整理とも異なる。そこで、解析処理を担当する Analyzer クラスを新しく作成する:

class Analyzer

  THRESHOLD = 0.09

  attr_reader :steps, :delta, :distance, :time

  def self.run(data, user, trial)
    analyzer = Analyzer.new(data, user, trial)
    analyzer.measure_steps
    analyzer.measure_delta
    analyzer.measure_distance
    analyzer.measure_time
    analyzer
  end

  def initialize(data, user, trial)
    @data  = data
    @user  = user
    @trial = trial
  end

  def measure_steps
    @steps = 0
    count_steps = true

    @data.each_with_index do |data, i|
      if (data >= THRESHOLD) && (@data[i-1] < THRESHOLD)
        next unless count_steps

        @steps += 1
        count_steps = false
      end

      count_steps = true if (data < 0) && (@data[i-1] >= 0)
    end
  end

  def measure_delta
    @delta = @steps - @trial.steps if @trial.steps
  end

  def measure_distance
    @distance = @user.stride * @steps
  end

  def measure_time
    @time = @data.count/@trial.rate if @trial.rate
  end

end

Analyzer クラスは最初に定数 THRESHOLD を定義する。この定数は低いピークを歩数と誤認するのを防ぐ閾値として利用される。議論を簡単にするため、多様で大規模な歩行データを解析して最適な THRESHOLD の値が求まっていると仮定する。この閾値を動的にして、ユーザーの歩行データをもとに変動させる学習アルゴリズムを実装することもできるだろう。

Analyzer の initialize メソッドは data, user, trial を受け取り、それらを対応するインスタンス変数 @data, @user, @trial に格納する。user と trial はそれぞれ User と Trial のインスタンスである。run メソッドは measure_steps, measure_delta, measure_distance, measure_time を順に呼び出す。順に見ていこう。

`measure_steps`

ついに！歩数計アプリで歩数を数えるコードを書くときがやってきた。measure_steps は最初に二つの変数を初期化する:

measure_steps は検知された歩数を数える。
count_steps は歩数を検知してよい状態にあるかどうかを表す。

この後 @processor.filtered_data の走査が始まる。現在の値が THRESHOLD 以上かつ一つ前の値が THRESHOLD 未満なら、加速度の時系列が閾値を下から上に通り過ぎているので、歩数の可能性がある。ただし、count_steps が false のときは見つかったピークに対応する歩数は既にカウントされているので、このときは unless を使って処理を飛ばす。count_steps が true なら @steps を 1 だけ増加させ、さらに count_step を false に設定して現在のピークをこれから歩数とカウントしないようにする。次の if 文は、時系列が \(x\) 軸を上から下に通り過ぎたときに count_steps を true に設定し、次のピークに備えるためにある。

これで歩数を測定するコードが完成した！ Processor クラスが時系列の整形や様々な周波数帯を除去して歩数の誤検知を防ぐ処理を行うので、実際に歩数を測定するコードは複雑ではない。

一度の歩行に対応する時系列全体がメモリ上に格納される事実は注目に値する。私たちが用意した歩行試行のデータはどれも短いので、こうしても今のところは問題は起こらない。ただ、多くのデータを持つ長い歩行も解析できることが求められる。理想的には、時系列の非常に小さな部分だけをメモリに保持するストリーム処理を実装するのが望ましい。この事実を念頭において、実装してきた処理は現在のデータ点と直前のデータ点だけを必要とするようにしてある。加えて、真偽値を使ったヒステリシスを実装してあるので、時系列が \(x\) 軸を通り過ぎた時刻を後から計算する必要はない。

プロダクトの将来を見据えた盤石な機能の設計と、プロダクトが必要とするかもしれない機能を思いつくままに実装するオーバーエンジニアリングの間には微妙なバランスがある。今回のケースでは、近い将来に長い歩行を扱う必要が生じると仮定するのは合理的であり、この仮定を考慮しながら歩数を測定するコストは小さい。

`measure_delta`

もし歩行試行のデータに実際の歩数が含まれるなら、measure_delta メソッドが計算された歩数と実際の歩数と差を計算する。

`measure_distance`

歩行距離はユーザーの歩幅と歩数を乗じることで計算できる。歩行距離は歩幅を利用して計算されるので、measure_distance の前に measure_steps を呼び出す必要がある。

`measure_time`

サンプリングレートさえ分かっていれば、経過時間は filtered_data に含まれるサンプル数をサンプリングレートで割ることで計算できる。こうして計算される値の単位は秒である。

全てをまとめるパイプライン

Parser, Processor, Analyzer クラスはそのままでも利用できるものの、一緒にした方が間違いなく使いやすい。私たちのプログラムは先述したパイプラインを実行することが多いので、Pipeline クラスを用意する:

class Pipeline

  attr_reader :data, :user, :trial, :parser, :processor, :analyzer

  def self.run(data, user, trial)
    pipeline = Pipeline.new(data, user, trial)
    pipeline.feed
    pipeline
  end

  def initialize(data, user, trial)
    @data  = data
    @user  = user
    @trial = trial
  end

  def feed
    @parser    = Parser.run(@data)
    @processor = Processor.run(@parser.parsed_data)
    @analyzer  = Analyzer.run(@processor.filtered_data, @user, @trial)
  end

end

お馴染みになった run パターンが使われている。まず Pipeline に加速度計からのデータと User, Trial のインスタンスが設定される。feed メソッドがパイプラインを実装する。このメソッドは加速度計からのデータを Parser.run に入力し、パースされたデータを今度は Processor.run に入力し、フィルタ後のデータを Analyzer.run に入力する。Pipeline が保持するインスタンス変数 @parser, @processor, @analyzer を使えば、パイプラインの実行後にアプリケーションが必要とするデータへアクセスできる。

使いやすいインターフェースの追加

最も手がかかる部分はこれで片付いた。続いて、ユーザーに分かりやすい形式でデータを表示するウェブアプリケーションを作成する。ウェブアプリケーションではデータの処理とデータの表示が自然に分離される。コードを書き始める前に、ユーザーの視点から何をすべきかを考えてみよう。

ユーザーシナリオ

ユーザーが /uploads にアクセスしてウェブアプリケーションを開始すると、既存のデータを示す表と新しいデータを送信するためのフォームを目にする。送信できるデータは加速度計が出力したファイルと歩行試行データ、そしてユーザー情報である (図 18)。

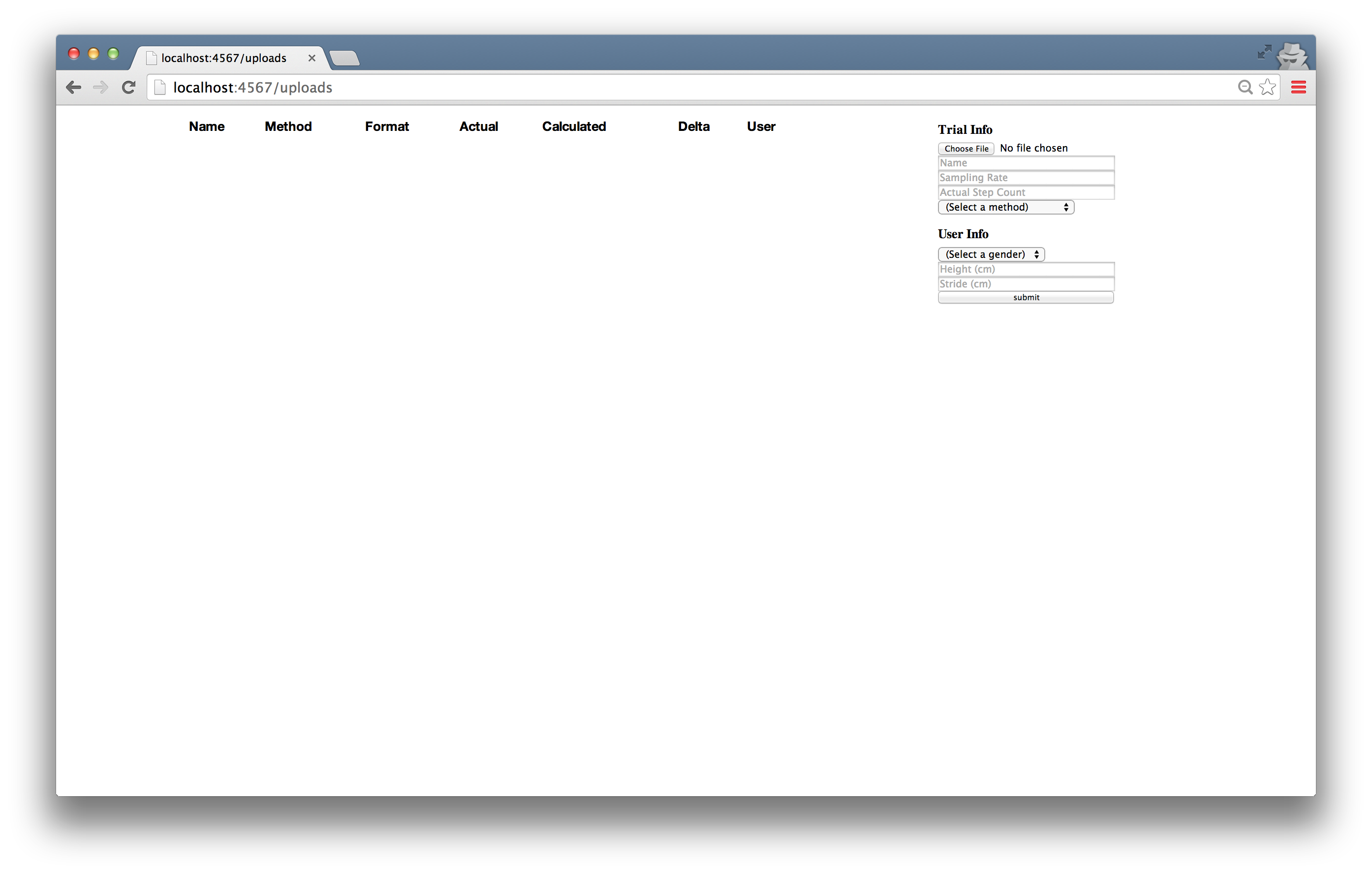
フォームを送信するとデータはファイルシステムに保存されてからパース・変形・解析され、ユーザーは表に新しい行が追加された /uploads にリダイレクトされる。

表の各行にある「Detail」リンクをクリックすると、対応するデータの詳細情報 (図 19) が表示される。

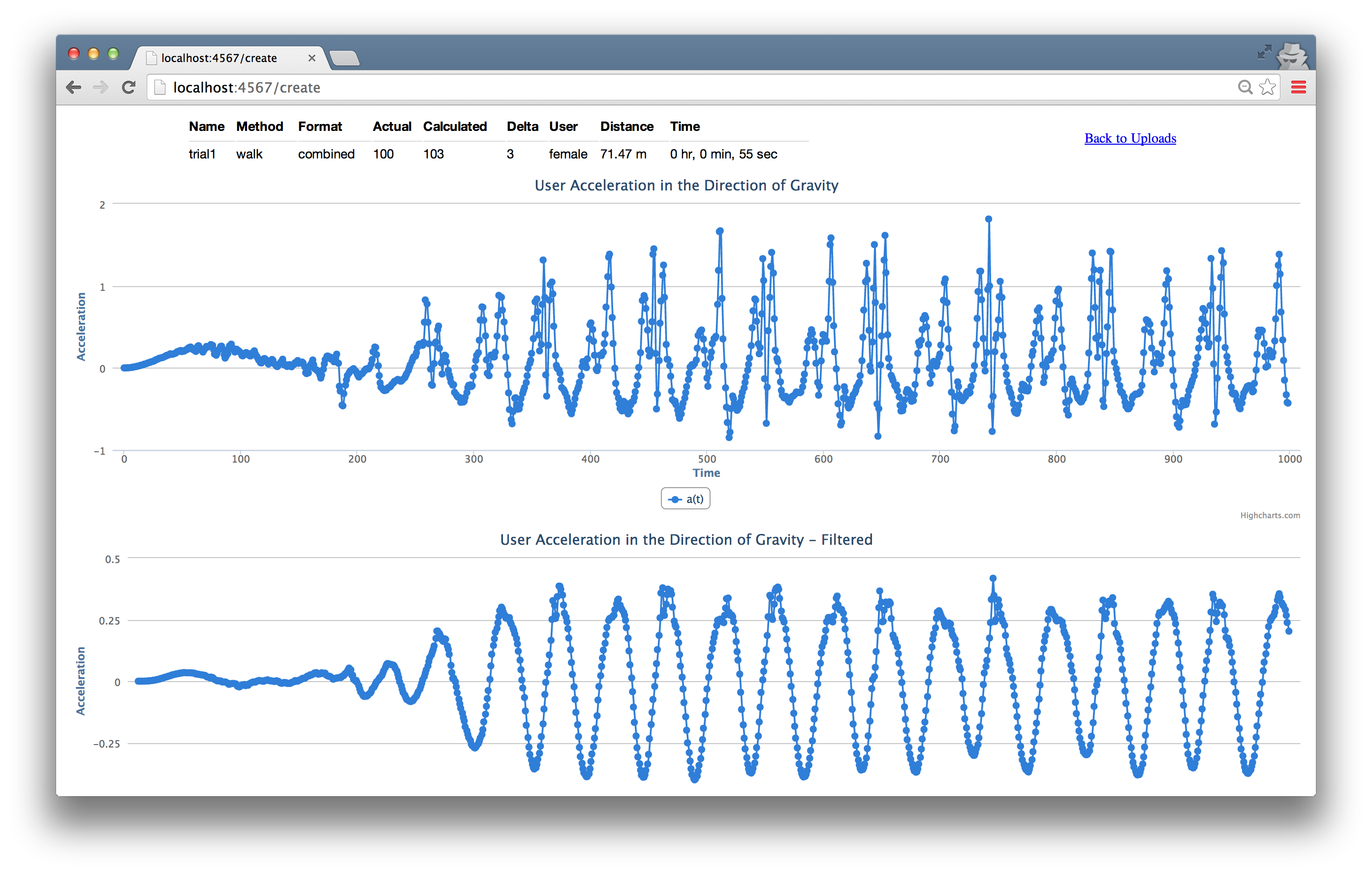
Detail ビューでは、ユーザーがフォームから送信した入力データ、プログラムが計算した値の一覧、内積を適用した後の時系列、フィルタを適用した後の時系列が表示される。ユーザーは「Back to Uploads」リンクから /uploads に戻ることができる。

こういった機能がウェブアプリケーションを実装する私たちにとって何を意味するかを見ていこう。まず、今までに使ってこなかった二つの重要な機能を提供するコンポーネントが必要になる:

ユーザーが入力したデータを保存・取得する。
基本的なインターフェースを備えたウェブアプリケーションを実行する。

二つのコンポーネントを一つずつ見ていく。

1. データの保存と取得

私たちのアプリケーションはファイルシステムを通じてデータを読み書きする。この処理は Upload クラスが担当する。このクラスはファイルシステム関係の処理を担当するだけで歩数計の実装とは直接関係ないので、ここではコードを省略する。ただ、その基本的な機能は議論に値する。Upload クラスはファイルシステムと対話するための三つのクラスレベルメソッドを持ち、どれも一つ以上の Upload のインスタンスを返す:

create は歩行試行に関する情報とファイルを入力として受け取る。入力のファイルはユーザーと歩行試行に関する情報を含んだファイル名でファイルシステムに保存される。インスタンス変数 @file_path, @user, @trial がそれぞれファイルパス、ユーザーオブジェクト、歩行試行オブジェクトに対するアクセスを与える。
find はファイルパスを受け取って Upload のインスタンスを返す。
all は Upload のインスタンスからなる配列を返す。返り値の配列には、ファイルシステムに保存された加速度計データファイルにつき Upload のインスタンスが一つ含まれる。

`Upload` における関心の分離

ここでも、関心の分離によってプログラムを上手く書くことができている。データの保存と取得に関するコードは全て Upload クラスに含まれるので、アプリケーションが成長して全てをファイルシステムに保存する代わりにデータベースを使うことになったとしても、Upload クラスを変更するだけで済む。このためリファクタリングが簡単かつ単純になる。

将来的には、User オブジェクトと Trial オブジェクトをデータベースに保存する設計も考えられる。このとき create, find, all メソッドは User と Trial のインスタンスも扱うことになる。さらに、データの保存と取得を一般的に扱うクラスを作成し、そのクラスを継承したクラスを User, Trial, Upload ごとに一つずつ作成するリファクタリングが行えるだろう。そのクラスにヘルパー用のクエリメソッドを追加して、プログラムの他の部分はそのクエリメソッドを使うようにもできるかもしれない。

2. ウェブアプリケーション

ウェブアプリケーションはこれまでに幾度となく書かれてきたので、オープンソースコミュニティの成果を活用して、面倒な仕事は既存のフレームワークに任せることにしよう。本プロジェクトでは Sinatra フレームワークを利用する。本人の言葉を借りるなら、Sinatra は「Ruby でウェブアプリケーションを素早く作成するための DSL」である。

私たちのウェブアプリケーションは HTTP リクエストに応答する必要があるので、応答できる HTTP メソッドと URL、そして実行される処理が書かれたコードブロック (ルート) を定義したファイルが必要になる。このファイルの名前は pedometer.rb としよう:

get '/uploads' do
  @error = "A #{params[:error]} error has occurred." if params[:error]
  @pipelines = Upload.all.inject([]) do |a, upload|
    a << Pipeline.run(File.read(upload.file_path), upload.user, upload.trial)
    a
  end

  erb :uploads
end

get '/upload/*' do |file_path|
  upload = Upload.find(file_path)
  @pipeline = Pipeline.run(File.read(file_path), upload.user, upload.trial)

  erb :upload
end

post '/create' do
  begin
    Upload.create(params[:data][:tempfile], params[:user], params[:trial])

    redirect '/uploads'
  rescue Exception => e
    redirect '/uploads?error=creation'
  end
end

この pedometer.rb があると、私たちのウェブアプリケーションは HTTP リクエストに対応するルートを使って応答できるようになる。各ルートのコードブロックは Upload クラスを使ってファイルシステムを利用したデータの格納または取得を実行し、その後ビューのレンダリングまたはリダイレクトを実行する。ビューはデータを表示するだけであり、私たちのアプリケーションの本筋ではない。そのためここでは省略する。

pedometer.rb で定義されるルートを一つずつ見ていこう。

`GET /uploads`

http://localhost:4567/uploads を開くと HTTP GET リクエストがウェブアプリケーションに送信され、get '/uploads' に続くコードが実行される。このコードはファイルシステムに保存されているアップロードされた全データに対してパイプラインを実行し、アップロードされたデータの一覧と新しいデータの送信フォームを持った uploads のビューをレンダリングする。エラーパラメータが含まれていた場合はエラー文字列が作成され、それが uploads で表示される。

`GET /upload/*`

各アップロードに対する「Detail」リンクをクリックすると、/upload/ にアップロードのファイルパスを付けた URL に対する HTTP GET リクエストが送信される。これを受けてパイプラインが実行され、upload ビューがレンダリングされる。このビューは HighCharts と呼ばれる JavaScript ライブラリを使って描画されるグラフをはじめとしたアップロードの詳細を表示する。

`POST /create`

最後のルートは /create に対する HTTP POST を処理するものであり、ユーザーが uploads ビューに含まれるフォームからデータをアップロードしたときに呼び出される。対応するコードブロックはユーザーがフォームに入力した値を params から取り出し、その値を使って新しい Upload のインスタンスを作成する。その後ユーザーは同じ /uploads にリダイレクトされる。データの処理中にエラーが発生した場合は /uploads の URL にエラーパラメータを設定し、何かが正しく完了しなかったことをユーザーに伝える。

完全な機能を持つウェブアプリケーション

完成だ！完全な機能を持つ、実際に利用できるウェブアプリケーションがこれで構築できた。

現実世界の問題に取り組むと、複雑で入り組んだ課題が現れる。ソフトウェアは、そういった課題を最小限のリソースで大規模に解決する力を持った特別な存在である。ソフトウェアエンジニアとして、私たちは自分たちの家庭やコミュニティ、そして世界にポジティブな変化をもたらすことができる。私たちが受ける訓練 (アカデミックなものであれ、実践的なものであれ) は、明確に定義された個別の問題を解決するコードを書く問題解決スキルを培うものである。ソフトウェアエンジニアとして成長して腕を磨く中で、その訓練で習ったことを乱雑な世界の現実がこれでもかと絡みついた実際の問題の解決に応用していかなければならない。本章を通じて、現実の問題を解決可能で小さな問題に切り分け、美しく、簡潔で、拡張可能なコードでそれを解決するプロセスを読者が体験できたことを願っている。

尽きることなく刺激的な世界で、興味深い問題を解決し続けよう。