18. 確率分布のサンプラー
18.1 はじめに
計算機科学と計算機工学では、数式を使って解決できない問題に直面することがよくある。そういった問題には複雑なシステムやノイズの含まれる入力が関係する。正確な解析解を持たない現実世界の問題の例をいくつか示す:
- 航空機のコンピューターモデルを作成し、様々な気象条件で航空機がどの程度安定するかを計算する。
- 建設予定の工場から漏出する化学物質が周辺地域の水道水に及ぼす影響を、地下水の拡散モデルを利用して計算する。
- カメラで取得したノイズの含まれる画像から、そこに写っている物体の三次元形状を復元する。
- チェスで特定の手を打ったときの勝率を計算する。
正確な解を求められない問題でも、モンテカルロ法 (Monte Carlo method) と呼ばれる手法を使うと近似解を求められる場合がある。モンテカルロ法の基本的な考え方は「大量のサンプル (sample) を生成し、そのサンプルを使って解を推定する」というものである1。
サンプリングとは何か?
サンプリング (sampling) とは、何らかの確率分布に沿った乱数を生成することを言う。サンプリングの結果として得られる値をサンプル (sample) と呼ぶ。例えば、六面のサイコロを振って出た目、シャッフルしたトランプの一番上にあるカード、ボードの中央を狙って投げたダーツが命中した位置はどれもサンプルと言える。こういった様々なサンプルの唯一の違いは生成に使われた確率分布 (probability distribution) である。サイコロの例では 6 個の値が同じ重みを持つ確率分布が使われ、トランプの例では 52 個の値が同じ重みをもつ確率分布が使われる。ダーツの例ではボードの中心が最も大きな重みを持ち、環状に重みが小さくなる確率分布が使われるだろう (ダーツを投げる人物の腕前によっては分布が一様にならない可能性もある)。
サンプルの利用法は主に二つある。まず、単にランダムな値を使いたい場合がある: 例えばポーカーのコンピューターゲームを実装するには、ランダムなカードを引く処理が必要になる。サンプルの二つ目の利用法は推定である。例えば、友人の使っているサイコロがイカサマではないかと疑っているとしよう。本当にイカサマかどうかを確かめるには、そのサイコロを何度も振ってみて、特定の目が他の目より多く出るかどうかを確認すればよい。また、上述の航空機の例のように、どの値がどのような確率で生成されるかを計算するときにもサンプルは利用できる。気象条件はカオス的な系なので、特定の気象条件で航空機が飛行できるかどうかを正確に計算することはできない。しかし、様々な異なる気象条件で何度も飛行機の振る舞いをシミュレートすれば、航空機が高い確率で飛行できない条件を発見できる。
サンプリングと確率のプログラミング
計算機科学の多くの応用と同じように、サンプリングと確率を利用するプログラムを書くときは様々なテクニックがコードの全体的な可読性・一貫性・正確性に影響する。本章では、コンピューターゲームでランダムなアイテムをサンプルするという単純な処理を例として用いながら、確率を扱うコードに特有なテクニックを解説する。例えばサンプリングや確率の評価を実行する関数、対数の利用法、再現性を確保する方法、サンプルの生成処理を特定のアプリケーションから分離する手法などが解説される。
記法について
確率変数 \(X\) が値 \(x\) を取る確率密度を \(p(x)\) などと表す記法を用いる。\(X\) が連続確率変数のとき \(p\) は確率密度関数 (probability density function, PDF) と呼ばれ、\(\displaystyle \int_{-\infty}^\infty p(x)\ \mathrm{d}x=1\) が成り立つ。\(X\) が離散確率変数のとき \(p\) は確率質量関数 (probability mass function, PMF) と呼ばれ、\(\displaystyle \sum_{x\in \mathbb{Z}} p(x)=1\) が成り立つ (\(\mathbb{Z}\) は全ての整数からなる集合を表す)。
ダーツがボードに刺さった位置の確率分布は連続の PDF であり、サイコロの出目の確率分布は離散の PMF である。両方の場合で、任意の \(x\) に対して \(p(x) \geq 0\) が成り立つ。つまり、確率は負にならない。
確率分布に関する一般的な操作が二つある。まず、与えられた値 \(x\) の特定の確率分布における確率密度を評価 (evaluate) する操作がある。数学的な記法を使えば、値 \(x\) の確率密度は \(p(x)\) と書ける。
そしてもう一つ、確率分布の PDF または PMF に比例するように (確率密度が大きい値がより頻繁に生成されるように) 値 \(x\) をサンプル (sample) する操作がある。数学的な記法を使えば、この操作は「\(x \sim p\) の生成」と言い換えられる。\(x \sim p\) は「値 \(x\) は確率密度が \(p(x)\) である確率分布に従う」を意味する。
18.2 魔法アイテムのサンプリング
確率が関連するコードを書くときに有用となるテクニックを見ていくための単純な例として、私たちは RPG ゲームを作っていて、モンスターを倒したときにドロップする魔法アイテムが持つランダムなステータスボーナスを生成するメソッドを書いている状況を考えよう。このアイテムが持つボーナスは最大でも \(+5\) で、上昇量が高いほど出現率が低く、具体的にはボーナスの値を表す確率変数を \(B\) とするとき次の等式を成り立たせたいとする:
また、ボーナスは六つのステータス (敏捷性、体力、筋力、知能、知恵、魅力) に配分されるとする。例えば \(+5\) のボーナスを持つアイテムであっても、ボーナスが複数のステータスに配分される (例えば体力 \(+2\) と知恵 \(+3\)) 場合もあれば、一つのステータスだけに割り振られる (例えば魅力 \(+5\) など) 場合もある。
この分布からランダムにサンプルするにはどうすればいいだろうか? おそらく最も簡単な方法は最初に全体のボーナス値をサンプルし、それから各ステータスにボーナスをランダムに割り振るものだろう。都合のいいことに、ボーナスの値の確率分布とボーナスの割り振りの確率分布はどちらも多項分布 (multinomial distribution) のインスタンスとして表現できる。
18.3 多項分布
多項分布は出力として可能な値が複数あり、それぞれの出力が特定の確率で出力されるときに利用できる。多項分布を説明する典型的な例として「ボールと壺問題 (ball and urn problem)」がある: 壺に様々な色が付いた (例えば 30% は赤色、20% は青色、50% は緑色の) ボールが大量に入っているとする。この壺からボールを一つ取り出して色を記録した後ボールを戻す操作を何度も繰り返すことを考える。このとき、多項分布の「出力」は特定の色が出た回数に対応し、それぞれの出力に対応する確率は各ボールの割合に対応する (例えば青い球を一つ取り出すという出力に対応する確率は \(p(\mathrm{blue})=0.20\) である)。多項分布を使うと、ボールを取り出す操作を何度か行ったとき特定の出力の組み合わせ (例えば「緑色が二つ、青色が一つ」) が起きる確率を計算できる。
本節のコードは multinomial.py にある。
MultinomialDistribution クラス
先述したように、確率分布を使う一般的な操作が二つある: その確率分布に沿って値をサンプルする操作と、確率分布の PDF または PMF を使ってサンプルを評価する操作である。これら二つの操作で必要となる計算は大きく異なるものの、必要となる情報は共通している: 確率分布のパラメータが決まっていなければ、サンプルも評価も実行できない。多項分布の場合には、パラメータとは事象確率 \(p\) を意味する。上記の例で言えば、\(p\) は壺に含まれる球の色の割合に対応する。
最も単純なアプローチを採用するなら、同じパラメータを持った (しかし実装は全く異なる) 二つの関数を作成することになる。しかし、私が確率を扱うコードを書くときは確率分布を表すクラスを用意する場合が多い。このアプローチには利点がいくつかある:
- パラメータを渡すのはクラスをインスタンス化するときだけで済む。
- 平均値、分散、微分といった確率分布に関する情報を取得したい場合がある。こういった情報を利用する関数を書く場合、パラメータを様々な関数に渡すより確率分布を表すクラスが持つメソッドを使う方がコードは格段に簡単になる。
- パラメータの値が正当かどうかを確認するのが望ましい (例えば多項分布では、事象確率を表すベクトル \(p\) の和が 1 でなければならない)。クラスのコンストラクタで一度だけ正当性を確認する方が、関数が呼ばれるたびに確認するより効率的である。
- PDF や PMF を扱う上でパラメータから求まる定数の計算が必要になる場合がある。クラスを使えば、この定数をコンストラクタで一度だけ事前に計算できる。クラスを使わないと、PDF や PMF を使うたびに定数を計算しなければならない。
実際の統計パッケージもクラスを用いた設計を採用している。例えば SciPy の scipy.stats モジュールには様々な確率分布を表すクラスが定義されている。ただ、本章では SciPy が提供する確率分布クラスは利用せずに、SciPy が提供する統計関数を利用する。クラスの動作を解説するため、そして現在の SciPy には多項分布を表すクラスが存在しないためである。
MultinomialDistribution クラスのコンストラクタを次に示す:
import numpy as np
class MultinomialDistribution(object):
def __init__(self, p, rso=np.random):
"""
多項分布に従う確率変数を初期化する。
引数
----------
p: 長さ k の NumPy 配列
事象確率
rso: numpy の RandomState オブジェクト (デフォルト: None)
乱数生成器
"""
# 事象確率の和が 1 であることを確認する。もし 1 でなければ
# 何かがおかしい! 浮動小数点数の誤差があるために和は正確に 1 には
# ならないので、np.isclose を使って判定する。
if not np.isclose(np.sum(p), 1.0):
raise ValueError("event probabilities do not sum to 1")
# 受け取った引数を保存する。
self.p = p
self.rso = rso
# self.p の各要素に対して対数を事前計算する。この対数確率は
# log-PMF で利用される。np.log に NumPy 配列を渡すと、
# 要素ごとの対数が計算される。
self.logp = np.log(self.p)
MultinomialDistribution クラスのコンストラクタは多項分布のパラメータである事象確率 p と、rso と呼ばれる変数を受け取る。コンストラクタは最初にパラメータが正当であること、つまり p の和が 1 であることを確認する。その後は受け取った引数を保存し、事象確率を使って事象対数確率 (後述) を計算する。rso オブジェクトは以降の処理で乱数を生成するために利用される (これについても後述)。
クラスの残りの部分を見ていく前に、このコンストラクタに関して言及しておきたい話題が二つある。
変数名に数学的な名前を使うべきか?
通常プログラマーは変数の名前の分かりやすさを重視する: 例えば independent_variable や dependent_variable は x や y より望ましい。一文字あるいは二文字の変数名は基本的に使うべきでないとされる。しかし、上に示した MultinomialDistribution クラスのコンストラクタは、典型的な命名ルールを破る p という名前の変数を使用している。
「変数には分かりやすい名前を付ける」という命名ルールに異論はない。しかし、数学に関するコードは例外だと私は思う。数学の書籍で示される数式では、変数の名前が \(x\), \(y\), \(\alpha\) といった一文字であることが多い。そのため、数式をコードにするときは x, y, alpha といった変数名を使うのが最も簡単な選択肢となる。もっと情報量の多い変数名が存在することは明らかである (x から得られる情報は少ない) ものの、変数名を長くすると数式とコードの対応関係が分かりにくくなってしまう。
数式を直接実装するコードを書くときは、数式で使われているのと同じ名前の変数を使うべきだと私は考える。そうすればコードのどの部分が数式のどの部分を実装しているかが分かりやすくなる。もちろん、コードだけを見たときの分かりやすさは損なわれるので、様々な計算の目標をコメントで詳しく説明することが非常に重要となる。もし数式が論文で示されたものなら、すぐに参照できるように論文の名前と論文中の式番号をコメントに書いておくべきである。
NumPy のインポート
numpy モジュールは np という名前でインポートされている。NumPy は便利な関数を大量に提供するので、一つのファイルから多くの関数を利用することもよくある。そのため numpy を np としてインポートすることが数値計算の世界における標準的な慣習となっている。本章の単純な例で利用する NumPy 関数は 11 個だが、ずっと多くなる可能性もある。プロジェクト全体で 40 個近くの NumPy 関数を使うことも珍しくない!
NumPy をインポートする方法はいくつかある。from numpy import * とすることもできる。しかし、こうすると NumPy 関数が他の関数と同じように使われてしまうので推奨されない。また、from numpy import array, log, ... として個別に関数をインポートすると、使う関数が増えたとき収集が付かない。単に import numpy とするのも一つの手だが、コードが非常に読みにくくなる。次の二つのコードはどちらも読みやすいとは言えないものの、numpy ではなく np を使ったコードの方がずっと読みやすい:
>>> numpy.sqrt(numpy.sum(numpy.dot(numpy.array(a), numpy.array(b))))
>>> np.sqrt(np.sum(np.dot(np.array(a), np.array(b))))
多項分布からのサンプリング
NumPy が提供する np.random.multinomial 関数を使えば、多項分布からサンプルを取得する処理を簡単に実装できる2。
しかし、この既存の関数を使うだけの処理にも、いくつか設計の選択肢がある。
乱数生成器のシード
サンプルをランダムに生成する場合でも、生成結果に再現性が求められるケースがある。ランダムに見える数値を生成しつつも、実行のたびに同じ「ランダム」な数列を生成できるのが望ましい。
こういった「再現性のあるランダム性」を持つ数値を生成するには、サンプリング関数に乱数の生成方法を伝える必要がある。NumPy の RandomState はこのために用意されるオブジェクトである。RandomState は本質的に乱数生成器であり、様々な関数に渡すことができる。実装されるメソッドは np.random が持つ関数と同様であり、乱数の生成元を制御できる点だけが関数と異なる。RandomState オブジェクトは次のように作成する:
>>> import numpy as np
>>> rso = np.random.RandomState(230489)
RandomState のコンストラクタに渡される整数は乱数生成器のシード (seed) を表す。同じシードで初期化された RandomState は同じ「乱数」を同じ順序で生成するので、再現性が保証される:
>>> rso.rand()
0.5356709186237074
>>> rso.rand()
0.6190581888276206
>>> rso.rand()
0.23143573416770336
>>> rso.seed(230489)
>>> rso.rand()
0.5356709186237074
>>> rso.rand()
0.6190581888276206
先述した MultinomialDistribution のコンストラクタには初期化済みの RandomState オブジェクトを引数 rso に渡すことができる。こういった乱数生成器を受け取る引数を私は省略可能にすることが多い: 乱数の再現性が必要ない場面もあるので、選択肢として用意する形にするのが望ましい (np.random モジュールの関数を直接使うと、この再現性の切り替えが不可能になる)。
そのためコンストラクタの引数に rso が与えられた場合は RandomState オブジェクトの多項分布サンプラーが使用され、与えられなかった場合は np.random.multinomial が使用される3。
どれがパラメータ?
np.random.multinomial と rso.multinomial のどちらを使うかを決めたら、後はそれを呼び出せばサンプリングを実行できる。しかし、考えなければならない要素がもう一つある: 使おうとしている確率分布のパラメータは何だろうか?
多項分布のパラメータは事象確率 \(p\) だと以前に説明した。しかし見方によっては、試行の回数 \(n\) も多項分布のパラメータと言えるかもしれない。だとしたら、MultinomialDistribution のコンストラクタに \(n\) が含まれていないのはどうしてだろうか?
この疑問は多項式分布に特有なものと思うかもしれないが、実際には確率分布を扱うとき頻繁に登場する疑問であり、答えは確率分布の使い道によって大きく異なる。多項分布の場合には、試行の回数が常に同じと仮定できるかどうかを考える必要がある。もし仮定できるなら、\(n\) をコンストラクタの引数として渡した方がよい。もし仮定できないなら、オブジェクトの作成時に \(n\) を固定すると振る舞いが非常に制限され、サンプルを生成するたびに新しい確率分布オブジェクトの作成が必要になる可能性さえある!
コードの振る舞いを制限したくはないので、私は \(n\) をサンプル生成メソッド sample の引数として、コンストラクタの引数とはしなかった。この他にも、\(n\) のデフォルト値をコンストラクタの引数で設定可能にした上で sample メソッドの引数で \(n\) を上書きできるようにする設計も考えられる。ただ、これは私たちの用途では機能過多に思えるため、sample メソッドだけに \(n\) を渡せる設計を採用する:
def sample(self, n):
"""
事象確率 self.p を持つ多項分布から n 回の試行をサンプルする。
引数
----------
n: 整数
試行回数
返り値
-------
長さ k の NumPy 配列
それぞれの事象が得られた回数
"""
x = self.rso.multinomial(n, self.p)
return x
多項分布の PMF の評価
今考えているシナリオでは、生成された魔法アイテムの確率を明示的に計算する必要はない。しかし、確率分布の PDF (probability density function, 確率密度関数) または PMF (probability mass function, 確率質量関数) を評価する関数 を実装して無駄になることはまずない。どうしてだろうか?
その理由の一つとしてテストがある: サンプリング関数を使って多くのサンプルを生成したとき、生成されるサンプルは PDF または PMF を近似しなければならない。大量のサンプルを生成しても近似が正確にならない場合には、コードのどこかにバグがあると分かる。
また、最初は気が付かなくても後で必要になることがよくあるというのも PDF または PMF を実装する理由となる。例えば、ランダムに生成されるアイテムに「コモン」「アンコモン」「レア」などの等級を割り振るときは PMF が必要になる。
最後に、多くの場合で確率分布を使った操作には PDF または PMF の実装が最初から必要になる。
多項分布の PMF
多項分布の PMF は次の数式で表される:
ここで \(\mathbf{x}=[x_1, \ldots{}, x_k]\) は長さ \(k\) のベクトルであり、各事象が起こった試行の回数を表す。同じく長さ \(k\) のベクトル \(\mathbf{p}=[p_1, \ldots{}, p_k]\) は各事象が起こる確率 (事象確率) を表す。上述したように、事象確率 \(\mathbf{p}\) は多項分布のパラメータである。
上記の式に含まれる階乗は実際にはガンマ関数 (gamma function) と呼ばれる特殊関数を使って表現される。ガンマ関数の方が階乗より扱いやすく効率的でもあるので、ガンマ関数を使って多項分布の PMF を書き直しておく:
対数の取り扱い
上記の式を実装するコードを見ていく前に、確率を扱うコードを書く上で最も重要なテクニックの一つをここで強調しておきたい: 対数の利用である。つまり、確率 \(p(x)\) を直接扱うのではなく、対数確率 \(\log{p(x)}\) を扱った方が計算は正確になる。確率は普通の計算をするだけでも非常に小さくなり、アンダーフローとそれに伴う誤差が発生する。そのため対数を取ると誤差を抑えることができる。
対数確率が必要な理由が分かる例を一つ示す。確率の値は \(0\) から \(1\) の間 (境界値含む) だったことを思い出してほしい。NumPy には実行中のシステムにおける浮動小数点数に関する情報を取得する finfo という便利な関数がある。例えば、Python の float 型が表す倍精度浮動小数点数が扱える最も小さい正の値は次のように取得できる:
>>> import numpy as np
>>> np.finfo(float).tiny
2.2250738585072014e-308
とても小さな値だと思うかもしれないが、この値と同程度の大きさの確率、あるいはもっと小さな確率に遭遇することは珍しくない。さらに、二つの確率の乗算はよくある操作であるものの、非常に小さな二つの確率を乗じるとアンダーフローが発生して精度が低下する:
>>> tiny = np.finfo(float).tiny
>>> # 非常に小さい数同士を乗じると、精度が全て失われる。
>>> tiny * tiny
0.0
しかし、確率の対数を取ると確率を通常より広い範囲の数値で表されるようになり、アンダーフローの問題が発生しにくくなる。確率の対数の値域は数学的には \(-\infty\) から \(0\) であり、コードにするときは倍精度浮動小数点数が表現可能な最小値 finfo(float).min から 0 が値域となる。この最小値は先述の tiny の対数より格段に小さい (対数を利用しなければ、この tiny が確率の下限となる)。
>>> # 確率の下限の対数 (通常時)
>>> np.log(tiny)
-708.39641853226408
>>> # 確率の下限の対数 (対数を使うとき)
>>> np.finfo(float).min
-1.7976931348623157e+308
つまり、対数を取った値を操作することで、表現可能な数の範囲を大きく拡大できる。さらに \(\log x y = \log x + \log y\) が成り立つので、対数を使うと乗算を加算で実行できる。このため、アンダーフローによって精度が落ちる問題も (それほど) 気にしないで済む:
>>> # 小さな確率の乗算
>>> np.log(tiny * tiny)
-inf
>>> # 小さな対数確率の加算
>>> np.log(tiny) + np.log(tiny)
-1416.7928370645282
もちろん、対数が魔法の弾丸というわけではない。例えば確率の加算などのために対数確率から通常の確率を計算すると、アンダーフローがまた姿を表す:
>>> tiny*tiny
0.0
>>> np.exp(np.log(tiny) + np.log(tiny))
0.0
しかし、確率の計算を全ての対数確率で行うことで多くの厄介な問題を回避できる。通常の確率に戻すときの精度の低下は避けられないかもしれないが、対数確率を使わなければ失われる情報がいくらか保持されるのは確かであり、その情報は例えば確率を比較するには十分である。
PMF を実装するコード
対数確率を考えることの重要性が分かったと思うので、次は対数 PMF を計算する関数を書こう:
def log_pmf(self, x):
"""
事象確率 self.p を持つ多項分布の、サンプル x に対する
対数確率質量関数 (log-PMF) を評価する。
引数
----------
x: 長さ k の NumPy 配列
各事象の発生回数
返り値
-------
サンプル x に対する log-PMF の評価結果
"""
# 試行回数の計算
n = np.sum(x)
# log(n!) と等価
log_n_factorial = gammaln(n + 1)
# log(x1! * ... * xk!) と等価
sum_log_xi_factorial = np.sum(gammaln(x + 1))
# self.p に 0 が含まれると、対応する self.logp の要素は -inf となる。
# 対応する x の要素が 0 だと次の乗算によって nan が得られる。
# しかし、その場合の乗算結果は 0 にしたいので、後から手動で調整する。
log_pi_xi = self.logp * x
log_pi_xi[x == 0] = 0
# log(p1^x1 * ... * pk^xk) と等価
sum_log_pi_xi = np.sum(log_pi_xi)
# パーツをまとめる。
log_pmf = log_n_factorial - sum_log_xi_factorial + sum_log_pi_xi
return log_pmf
多くの部分は上述した多項分布の PMF の数式をそのまま実装している。gammaln 関数は scipy.special モジュールに含まれる関数であり、対数ガンマ関数 \(\log \Gamma(x)\) を計算する。先述したように、階乗関数よりガンマ関数の方が扱いやすい: SciPy は対数ガンマ関数を提供するのに対して、対数階乗関数は提供しない。階乗関数を使うとしたら、次のようなコードとなるだろう:
log_n_factorial = np.sum(np.log(np.arange(1, n + 1)))
sum_log_xi_factorial = np.sum([np.sum(np.log(np.arange(1, i + 1))) for i in x])
しかし SciPy が提供する対数ガンマ関数を使えば、これより可読性と効率に優れるコードを簡単に書くことができる。
対処すべきコーナーケースが一つある: 事象確率に \(0\) が含まれる場合である。\(p_i=0\) のとき \(\log{p_i}=-\infty\) となる。こうなっても問題ない場合も多いものの、\(\log p_i\) に \(0\) を乗じるときは nan となって問題が発生する:
>>> # 無限大に整数を乗じるのは問題ない...
>>> -np.inf * 2.0
-inf
>>> # ...しかし 0 を乗じると問題が発生する。
>>> -np.inf * 0.0
nan
nan は「数でない (not a number)」ことを意味する。ほとんどの演算は nan がオペランドに含まれるとき結果も nan となる。そのため \(p_i = 0\) かつ \(x_i = 0\) のケースをそのままにしておくと nan が他の配列にも入り込むことになり、望ましくない。そこで上記のコードでは \(x_i=0\) が成り立つケースを特別扱いして「\(x_i = 0\) のとき \(x_i \log p_i = 0\)」を成り立たせている。
少しの間だけ対数確率を使う理由に関する議論に戻る。本当に必要なのが log-PMF ではなく PMF である場合でも、log-PMF を最初に計算してから指数関数を適用した方が一般に優れた結果が得られる:
def pmf(self, x):
"""
事象確率 self.p を持つ多項分布の、サンプル x に対する
確率質量関数 (PMF) を評価する。
引数
----------
x: 長さ k の NumPy 配列
各事象の発生回数
返り値
-------
サンプル x に対する PMF の評価結果
"""
pmf = np.exp(self.log_pmf(x))
return pmf
多項分布を使った次の例を見るだけでも、対数確率で計算を進めることの重要性が確認できる:
>>> dist = MultinomialDistribution(np.array([0.25, 0.25, 0.25, 0.25]))
>>> dist.log_pmf(np.array([1000, 0, 0, 0]))
-1386.2943611198905
>>> dist.log_pmf(np.array([999, 0, 0, 0]))
-1384.9080667587707
上記のコードで計算される二つの確率は極端に小さい (以前の実行結果と比べると、tiny よりずっと小さいことが分かる)。これは PMF の分母が巨大なためである: \(100!\) はオーバーフローするので通常の方法では計算できない。しかし \(\log 100!\) ならば計算できる:
>>> from scipy.special import gamma, gammaln
>>> gamma(1000 + 1)
inf
>>> gammaln(1000 + 1)
5912.1281784881639
上記の PMF を gamma 関数を利用して計算すると、途中で gamma(1000 + 1) / gamma(1000 + 1) の計算が必要になって nan が生成される (正しい値は当然 1 である)。しかし対数確率を使って計算を進めれば、こういった問題は起こらない!
18.4 魔法アイテムのサンプリング (再訪)
以上で多項分布を表すオブジェクトのコードが書けたので、先述した魔法アイテムを生成する処理で使ってみよう。この処理を実装するために MagicItemDistribution と呼ばれるクラスを作成する。本節のコードは rpg.py ファイルにある:
class MagicItemDistribution(object):
# 魔法アイテムが影響を及ぼすステータスの名前 (と順番) の定義
stats_names = ("dexterity", "constitution", "strength",
"intelligence", "wisdom", "charisma")
def __init__(self, bonus_probs, stats_probs, rso=np.random):
"""
魔法アイテムの確率分布を初期化する。bonus_probs と stats_probs を
確率分布のパラメータとして用いる。
引数
----------
bonus_probs: 長さ m の NumPy 配列
ボーナスの総量の確率を表す。配列の添え字がボーナスの総量に
対応する。例えば bonus_probs[0] にはボーナスの総量が +0 となる
確率が、bonus_probs[1] にはボーナスの総量が +1 となる確率が
格納される。
stats_probs: 長さ 6 の NumPy 配列
ボーナスが各ステータスに割り当てられる確率を表す。1 ポイントの
ボーナスをいずれかのステータスに割り当てるとき、i 番目の
ステータス (MagicItemDistribution.stats_names[i]) にボーナスが
割り当てられる確率が stats_probs[i] となる。
rso: numpy RandomState object (デフォルト: np.random)
乱数生成器
"""
# 使用する多項分布オブジェクトを作成する。
self.bonus_dist = MultinomialDistribution(bonus_probs, rso=rso)
self.stats_dist = MultinomialDistribution(stats_probs, rso=rso)
この MagicItemDistribution クラスのコンストラクタはボーナスの総量が従う確率分布のパラメータ、ステータス割り当てが従う確率分布のパラメータ、そして乱数生成器を引数に取る。ボーナスの総量が従う確率分布は以前に具体的に示したものの、確率分布のパラメータを引数として渡すことは一般に良いアイデアである。こうすれば他の確率分布を使ったアイテムのサンプリングが可能になる (例えば、プレイヤーのレベルが上がったときにボーナスの総量の確率を変えることになるかもしれない)。ステータスの名前はクラス変数 stats_names にハードコードされるものの、コンストラクタの引数にすることも当然できる。
先述の通り、魔法アイテムのサンプリングは二つのステップからなる: 最初にボーナスの総量をサンプルし、それから各ステータスに対するボーナスの配分をサンプルする。これら二つのステップは _sample_bonus と _sample_stats の二つのメソッドで実装される:
def _sample_bonus(self):
"""
ボーナスの総量をサンプルする。
返り値
-------
整数
ボーナスの総量
"""
# ボーナスの総量は n=1 (試行を一度だけ行うとき) の多項分布
# からのサンプルに等しい。
sample = self.bonus_dist.sample(1)
# sample の要素は一つだけが 1 で、それ以外は全て 0 である。
# 1 の要素の位置がサンプルされたボーナスの総量に等しい。
# sample からボーナスの総量を取得する。
bonus = np.argmax(sample)
return bonus
def _sample_stats(self):
"""
ボーナスの総量、そして各ステータスに対するボーナスの割り当てをサンプルする。
返り値
-------
長さ 6 の NumPy 配列
各ステータスに対するボーナス
"""
# まずボーナスの総量をサンプルする。
bonus = self._sample_bonus()
# 次に、別の多項分布を使ってボーナスの割り当てをサンプルする。
# ボーナスの総量が試行回数に対応する。
stats = self.stats_dist.sample(bonus)
return stats
_sample_stats は _sample_bonus に依存する唯一の関数なので、これらの処理を一つのメソッドで実装することも選択肢に入る。二つのメソッドに分けているのは、メソッドが小さいと理解しやすくなり、テストも容易になるためである。
これらのメソッドが名前の先頭にアンダースコアを持つことに気が付いただろう。このアンダースコアはクラスの外側からそのメソッドを直接利用すべきでないことを示す。クラスの外側から利用できるメソッドとしては次の sample が提供される:
def sample(self):
"""
ランダムな魔法アイテムをサンプルする。
返り値
-------
辞書
キーにはステータスの名前、バリューには対応するステータスに
割り当てられたボーナスの量が格納される。
"""
stats = self._sample_stats()
item_stats = dict(zip(self.stats_names, stats))
return item_stats
ステータスの名前をキーに持つ辞書を返すことを除けば、sample 関数の処理は _sample_stats と本質的に変わらない。しかしこうすることで、魔法アイテムをサンプルするための明確で理解しやすいインターフェースが提供されている: 各ステータスのボーナスは返り値からすぐに分かる ── それでいて、多くのサンプルが必要で効率が求められる場合は直接 _sample_stats を利用できる。
魔法アイテムの確率を評価する処理でも同様の設計を用いる。具体的には、sample が返す形式の辞書を受け取る高レベルなメソッド pmf と log_pmf が公開される:
def log_pmf(self, item):
"""
与えられた魔法アイテムの対数確率を計算する。
引数
----------
item: 辞書
キーはステータスの名前、バリューは対応するステータスに
割り当てられるボーナスの量を意味する。
返り値
-------
float
数値 log(p(item))
"""
# 各ステータスに対するボーナスを正しい順番で抽出し、
# それを _stats_log_pmf に渡す。
stats = np.array([item[stat] for stat in self.stats_names])
log_pmf = self._stats_log_pmf(stats)
return log_pmf
def pmf(self, item):
"""
与えられた魔法アイテムの確率を計算する。
パラメータ
----------
item: 辞書
キーはステータスの名前、バリューは対応するステータスに
割り当てられるボーナスの量を意味する。
返り値
-------
float
数値 p(item)
"""
return np.exp(self.log_pmf(item))
これらのメソッドが利用する _stats_log_pmf は各ステータスに対するボーナスの量から確率を計算するメソッドであり、辞書ではなく配列を受け取る:
def _stats_log_pmf(self, stats):
"""
各ステータスに対するボーナスの配分を受け取り、
その log-PMF を評価する。
引数
----------
stats: 長さ 6 の NumPy 配列
各ステータスに対するボーナスの配分
返り値
-------
float
数値 log(p(stats))
"""
# ボーナスは必ず全て割り振られるので、stats の和はボーナスの
# 総量に等しい。
total_bonus = np.sum(stats)
# ボーナスの総量が total_bonus となる確率を計算する。
logp_bonus = self._bonus_log_pmf(total_bonus)
# 各ステータスに対するボーナスが stats となる確率を計算する。
logp_stats = self.stats_dist.log_pmf(stats)
# 二つの確率の積を返す (対数確率を考えているので加算で計算できる)。
log_pmf = logp_bonus + logp_stats
return log_pmf
この _stats_log_pmf が呼び出す _bonus_log_pmf は、ボーナスの総量の確率を計算する:
def _bonus_log_pmf(self, bonus):
"""
ボーナスの総量を受け取り、その log-PMF を評価する。
引数
----------
bonus: 整数
ボーナスの総量
返り値
-------
float
数値 log(p(bonus))
"""
# 引数 bonus の値が正当であることを確認する。
if bonus < 0 or bonus >= len(self.bonus_dist.p):
return -np.inf
# スカラーの bonus を試行結果と同様のベクトルに変換する。
x = np.zeros(len(self.bonus_dist.p))
x[bonus] = 1
return self.bonus_dist.log_pmf(x)
以上のコードがあれば、魔法アイテムの確率分布を表すオブジェクトを次のように作成できる:
>>> import numpy as np
>>> from rpg import MagicItemDistribution
>>> bonus_probs = np.array([0.0, 0.55, 0.25, 0.12, 0.06, 0.02])
>>> stats_probs = np.ones(6) / 6.0
>>> rso = np.random.RandomState(234892)
>>> item_dist = MagicItemDistribution(bonus_probs, stats_probs, rso=rso)
作成した MagicItemDistribution オブジェクトを使うと何度でも魔法アイテムを作成できる:
>>> item_dist.sample()
{'dexterity': 0, 'strength': 0, 'constitution': 0,
'intelligence': 0, 'wisdom': 0, 'charisma': 1}
>>> item_dist.sample()
{'dexterity': 0, 'strength': 0, 'constitution': 1,
'intelligence': 0, 'wisdom': 2, 'charisma': 0}
>>> item_dist.sample()
{'dexterity': 1, 'strength': 0, 'constitution': 1,
'intelligence': 0, 'wisdom': 0, 'charisma': 0}
サンプルされたアイテムの確率を評価することもできる:
>>> item = item_dist.sample()
>>> item
{'dexterity': 0, 'strength': 0, 'constitution': 0,
'intelligence': 0, 'wisdom': 2, 'charisma': 0}
>>> item_dist.log_pmf(item)
-4.9698132995760007
>>> item_dist.pmf(item)
0.0069444444444444441
18.5 攻撃ダメージの推定
これまでに「モンスターがドロップするランダムなアイテムの生成」というサンプリングの応用を一つ見た。本章の最初で説明したように、確率分布からのサンプリングは値の推定にも利用できる。これから MagicItemDistribution を使って値を推定する例を説明する。今考えている RPG ゲームでは攻撃したときのダメージが十二面サイコロによって決定され、「腕力」ステータスに対するボーナスの分だけ攻撃時に振るサイコロの個数が増えるとしよう。例えば「腕力」ステータスに \(+2\) のボーナスがあるときは三つのサイコロを振ることができる。与えるダメージは出目の和に等しいとする。
敵モンスターの強さを調整するために、特定の個数の魔法アイテムを持つプレイヤーが攻撃したときのダメージがどれくらいかを知りたい状況があるかもしれない。例えば二つの魔法アイテムを持っているプレイヤーの 50% が三回の攻撃で敵を倒せるようにしたいとき、敵の HP をいくつに設定すべきだろうか?
この問題の解決法の一つにサンプリングを使うものがある。この解決法は次のステップからなる:
- 二つの魔法アイテムをランダムにサンプルする。
- 魔法アイテムが持つ「腕力」ステータスに対するボーナスから、攻撃時に振られるサイコロの個数を計算する。
- 計算されたサイコロの個数を使って、三回の攻撃で与えられる総ダメージをサンプルする。
- 以上のステップを何度も繰り返し、総ダメージが従う確率分布の近似を得る。
ダメージの確率分布の実装
prg.py に含まれる次の DamageDistribution クラスが上記の処理を実装する:
class DamageDistribution(object):
def __init__(self, num_items, item_dist,
num_dice_sides=12, num_hits=1, rso=np.random):
"""
攻撃時のダメージが従う確率分布を表すオブジェクトを初期化する。
このオブジェクトは num_items 個の魔法アイテムを持つプレイヤーが
num_hits 回の攻撃で与えるダメージをサンプルできる。各攻撃は
num_dice_sides 面のサイコロを使って決定される。
引数
----------
num_items: int
プレイヤーが持っている魔法アイテムの個数
item_dist: MagicItemDistribution object
魔法アイテムが従う確率分布を表すオブジェクト
num_dice_sides: int (デフォルト: 12)
サイコロの面数
num_hits: int (デフォルト: 1)
攻撃回数
rso: numpy RandomState object (デフォルト: np.random)
乱数生成器
"""
# サイコロの各面の出目を収めた配列を作成する。
self.dice_sides = np.arange(1, num_dice_sides + 1)
# サイコロを振ったときの出目が従う多項分布を表す
# 多項分布オブジェクトを作成する。各面は同じ確率を持つ。
self.dice_dist = MultinomialDistribution(
np.ones(num_dice_sides) / float(num_dice_sides), rso=rso)
self.num_hits = num_hits
self.num_items = num_items
self.item_dist = item_dist
def sample(self):
"""
攻撃時のダメージをサンプルする。
返り値
-------
int
サンプルされたダメージ
"""
# まず、コンストラクタで指定された個数の魔法アイテムをサンプルする。
items = [self.item_dist.sample() for i in xrange(self.num_items)]
# サンプルされた魔法アイテムの「腕力」ステータスから、
# 振るサイコロの個数を計算する。
num_dice = 1 + np.sum([item['strength'] for item in items])
# サイコロを振り、最終的なダメージを計算する。
dice_rolls = self.dice_dist.sample(self.num_hits * num_dice)
damage = np.sum(self.dice_sides * dice_rolls)
return damage
この DamageDistribution クラスのコンストラクタはサイコロの面数、ダメージを計算するときの攻撃回数、プレイヤーが持つ魔法アイテムの個数、魔法アイテムのボーナスが従う確率分布 (MagicItemDistribution 型のオブジェクト)、そして乱数生成器オブジェクトを受け取る。サイコロの面数は厳密にはパラメータであるものの変化する可能性が低いので、num_dice_side にはデフォルト値 12 が設定される。同様に、一度の攻撃のダメージをサンプルすることが多いので、num_hits にはデフォルト値 1 が設定される。
実際のサンプリングは sample メソッドで実装される (MagicItemDistribution.sample メソッドと似た構造を持つ点に注目してほしい)。最初にプレイヤーが持つ魔法アイテムの集合をサンプルし、それらの魔法アイテムが持つ「腕力」ステータスへのボーナスの総量を計算する。最後に (信頼できる多項分布オブジェクトをここでも利用して) サイコロを振れば、総ダメージを計算できる。
確率の評価はどうなった?
上記の DamageDistribution クラスに log_pmf メソッドや pmf メソッドが含まれていないことに気が付いたかもしれない。その理由は、PMF がどんな関数か分からないからである! PMF を数式で表すことはできる:
この数式を計算するには、総ダメージとして可能な値、そして \(m\) 個の魔法アイテムとして可能な組み合わせを全て考える必要がある。総当たりによる計算は不可能ではないものの、とてつもない時間がかかるだろう。実は、これは正確な解を計算できない問題に対してサンプリングを使って近似解を計算する完璧な例と言える。そのため PMF の計算方法ではなく、大量のサンプルを使って確率分布を近似する方法をこれから説明する。
確率分布の近似
先述した疑問「二つの魔法アイテムを持っているプレイヤーの 50% が三回の攻撃で敵を倒せるようにしたいとき、敵の HP はいくつに設定するべきか?」に答える準備が整った。
まず、考えている確率分布を表すオブジェクトを作成する。以前に作成した item_dist と rso が再利用できる:
>>> from rpg import DamageDistribution
>>> damage_dist = DamageDistribution(2, item_dist, num_hits=3, rso=rso)
後はサンプルを大量に生成し、50 パーセンタイル (サンプルの 50% より大きい値) を計算すればよい:
>>> samples = np.array([damage_dist.sample() for i in xrange(100000)])
>>> samples.min()
3
>>> samples.max()
154
>>> np.percentile(samples, 50)
27.0
ダメージの値ごとに生成されたサンプルの個数をプロットすると、図 1 のような画像が得られる。
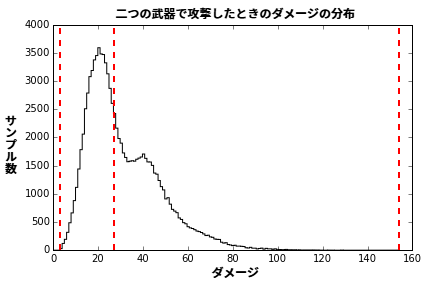
このグラフからは、プレイヤーが与えるダメージの総量には非常に広い幅があることが分かる。一方で、その裾は長い: 50 パーセンタイルは 27 であり、これはプレイヤーの半分は 27 ポイントのダメージしか与えられないことを意味する。そのため先述の基準を元に難易度を決めるのであれば、敵の HP を 27 にすべきだと結論できる。
18.6 まとめ
本章では、名前の付いた関数では表せない複雑な確率分布に従うサンプルを生成するコード、そして生成されたサンプルの確率を評価するコードを解説した。その中で見た具体例には、一般的なケースにも応用できるテクニックが含まれていた:
- 確率分布をクラスで表現し、サンプリングを行うメソッドと PDF (または PMF) を評価するメソッドの両方を実装する。
- PDF (または PMF) の対数を計算する。
- 再現性を保証するために、サンプリングで乱数生成器オブジェクトを利用する。
- 入力と出力が明確で理解しやすい関数 (例えば、使いやすさを重視して辞書を出力する
MagicItemDistribution.sample) を用意しつつも、純粋に数値だけを扱う同じ処理の効率的なバージョン (MagicItemDistribution._sample_stats) も用意しておく。
さらに、確率分布からのサンプリングは単一のランダムな値 (例えば、倒したモンスターがドロップする魔法アイテム) の生成に利用できるのに加えて、他の方法では知ることのできない確率分布に関する情報 (例えば、二つの魔法アイテムを持つプレイヤーが攻撃したときのダメージの 50 パーセンタイル) を計算するのにも利用できることを見た。サンプリングが使われる場面を目にするとしたら、まず間違いなくこれら二つのいずれかとなる。サンプルを生成する確率分布が変わるだけで、コードの一般的な構造はそれほど変わらない。
-
本章は統計と確率に関する基本的な知識を仮定する。 ↩︎
-
NumPy には様々な確率分布からサンプルを取得する関数が含まれる。完全なリストはランダムサンプリングモジュール
np.randomのドキュメントから確認できる。 ↩︎ -
np.randomモジュールの関数は NumPy が持つグローバルな乱数生成器を利用するので、np.seedでグローバルなシードを設定すれば振る舞いを制御できる。グローバルな乱数生成器とローカルなRandomStateオブジェクトの間にはトレードオフがある。グローバルな乱数生成器を使うとRandomStateオブジェクトをあらゆる処理に受け渡す必要がなくなる一方で、第三者のコードが知らないうちにグローバルな乱数生成器を使う可能性を排除できなくなる。ローカルなRandomStateオブジェクトを使えば、自分で書いていないコードが原因の非決定性を見つけやすくなる。 ↩︎