プリミティブアセンブリ

目次

テクスチャサンプラーに関する章が終わり、私たちは 3D フロントエンドに戻ってきた。これで頂点シェーディングが完了したから、これでやっとレンダリングが始まるはずだ... いや、そうはいかない。なぜって、プリミティブのラスタライズを始める前に必要な処理がたっぷりある。どれくらいあるかと言うと、この章ではラスタライズを一切説明できないぐらいたくさんある──ラスタライズは次章まで待たなければならない。

プリミティブアセンブリ

頂点パイプラインに戻ると、シェーディングの終わった頂点のブロックがシェーダーユニットから返ってくる。そのブロックには整数個のプリミティブが含まれるという暗黙の約束がある──つまり、一つの三角形・直線・パッチが複数のブロックにまたがることはない。この約束があると各ブロックを完全に独立に扱うことができ、頂点シェーダーから出力されるブロックは一つだけバッファすれば済むようになるので、非常に重要である。二つ以上のブロックをバッファすることは当然できるが、する必要があるわけではない。

次のステップでは単一のプリミティブに属する全ての頂点の組み立てアセンブリが行われる (だから「プリミティブアセンブリ」と呼ばれる)。プリミティブが点なら、一つの頂点を読んで次のステップで渡すだけとなる。直線なら頂点は二つで、三角形なら三つだ。制御点を多く持つパッチならさらに多くなる。

簡単に言えば、頂点を集める処理がここで起こる全てである。これを行うには、「頂点インデックス → キャッシュ位置」というマップ (前に説明したキャッシュタグアレイ) のコピーを保持しておいて元のインデックスバッファを読む方法もあるし、完全に展開されたプリミティブにおけるインデックスをシェーディング後の頂点データと共に最初から用意しておく方法もある。後者の方法だと頂点シェーダーの出力をバッファするための空間が多く必要になるかもしれないが、ここでインデックスバッファを読まなくて済む。どちらの方法でも問題はない。

これでプリミティブを構成する全ての頂点が展開された。言い換えると、ただの頂点の並びではなく、完全な三角形のリストが手に入った。ではラスタライズを始められるのだろうか？ いやまだだ。

ビューポートカリングとクリッピング

あぁそうだ、これがある。そうだ、これを最初に片付けないといけない。これはパイプラインの中でもあなたが想像する通りのことを行うモジュールの一つであり、おそらくはその方法も想像する通りである (つまり様々な書籍で説明される方法と同じだ)。というわけでポリゴンクリッピングを一般的に説明することはしないので、適当なコンピューターグラフィックスの教科書を見てほしい。ただ、たいていの本にある説明はかなりひどい。もし分かりやすい説明を探しているなら、Jim Blinn による A Trip Down the Graphics Pipeline の 13 章を勧める。そのとき彼が使っているクリップ空間 \([0,w]\) は今では使われていないので、混乱を避けるために頭の中で読み替えた方がよいだろう。

さて、クリッピングだ。短くまとめるとこうなる: 頂点シェーダーが返すのは同次クリップ空間における頂点座標である。この空間は視錐台を表す方程式が可能な限り簡単になるように選ばれており、D3D における視錐台の方程式は \(-w \leq x \leq w\), \(-w \leq y \leq w\), \(0 \leq z \leq w\), \(0 < w\) である。最後の条件は同次点 \((0,0,0,0)\) (一種の退化) を除外するためだけにある。

考えている三角形が部分的あるいは完全にクリップ面の外にないかどうかを最初に判定する必要がある。これは Cohen-Sutherland スタイルのアウトコード (outcode) を使うと非常に効率的に行える。まず各頂点に対するクリップアウトコード (単にクリップコードとも呼ばれる) を計算する (例えば頂点シェーディング時に計算して位置と共に保存する)。すると各プリミティブに対して、各頂点のクリップコードのビット AND はプリミティブに含まれる全ての頂点が外側にあるような視錐台平面を表す (もし一つでもこういった平面が存在するなら、そのプリミティブ全体が視錐台の外側にあるので破棄して構わない)。またクリップコードのビット OR は、そのプリミティブに対してクリップを行う必要のある平面を表す。こういった処理はハードウェアでは数個のゲートで行える簡単な仕事である。

加えて、頂点シェーダーは各頂点に対する「カリング距離 (cull distance)」や「クリップ距離 (clip distance)」を生成することもできる: 各頂点に対するカリング距離が全てゼロより小さい三角形は破棄され、クリップ距離は追加のクリップ平面を定義する。これらの値はプリミティブを破棄/クリップするテストで考慮される。

実際のクリップ処理は (もし起動されるなら) 二つの形態のいずれかで行われる: 実際にポリゴンクリッピングのアルゴリズムを走らせる (頂点と三角形を追加する) 方法と、クリップ平面をラスタライザに対する追加の方程式として渡す方法のいずれかである (後者は聞きなれない方法かもしれないが、ラスタライザを説明する次章まで待ってほしい──最後には全て理解できる)。方程式を追加する方法はエレガントでポリゴンのクリップを必要としないが、正規化された 32 ビットの浮動小数点数を正当な頂点座標として受け取らなくてはならなくなる。これを行う高速なハードウェアラスタライザを構築するトリックがもしかしたら存在するかもしれないが、少なくとも手のかかる方法と言える。そのためここではクリッピングが (三角形の追加などを含めて全て) 存在するものとして話を進める。クリッピングは厄介だが、非常にまれにしか起きないので大きな問題ではない (すぐに説明するように、頻度はあなたが思うよりも少ない)。実際のクリッピングが特殊なハードウェアで行われるか、それともシェーダーユニットを拝借して行われるかは場合による。この判断に影響する要素としては、このステージにおける新しい頂点シェーディングロードのディスパッチが不格好でないかどうか、専用クリッピングユニットがどれくらいの大きさか、専用クリッピングユニットがどれくらい必要か、などがある。こういった質問の答えを私は知らないが、少なくともパフォーマンスの観点から考えると、二つの方法は大きく違わない: クリップはたまにしか起きないからだ。これはガードバンドクリッピングを使える理由でもある。

ガードバンドクリッピング

この名前は適切でない: ガードバンドクリッピングはクリッピングを行う洗練された方法ではない。その反対で、クリッピングを行わない簡単な方法である :)

元となるアイデアは非常に単純だ: 上下左右のクリップ平面から少しだけはみ出るプリミティブの大部分は、クリップする必要が全くない。GPU における三角形のラスタライズは事実上、スクリーンエリア (正確にはシザーレクト) 全体をスキャンし、全てのピクセルに対して「このピクセルは現在の三角形によって覆われるか？」を判定することで動作する (実際はもっと複雑ではるかに効率的だが、一般的なアイデアとしてはこうなっている)。この処理は完全にビューポートに収まっている三角形だけではなく、クリッピング面の例えば右と上にはみ出している三角形に対しても正しく動作する。つまり三角形の被覆判定が信頼できるものである限り、上下左右の平面に対してはクリップが必要とならない！

ただし、通常この三角形の被覆判定は適当な固定精度の整数算術で行われる。よって三角形の頂点を遠くへ遠くへと移動させると、いずれ整数のオーバーフローが起きて間違った判定結果が得られるようになる。ラスタライザが実際にはビューポートの内側に存在しない三角形のピクセルを生成するというのは、ごく控えめに言っても非常に無礼な振る舞いであり、非合法であるべきだというのは誰でも納得できると思う！ これは実際そうなっている──そういったことを行うハードウェアは仕様を満たさないとされる。

この問題には二つの解決法がある: 一つは三角形の被覆判定が入力の三角形がどんなものであれ絶対に間違った結果を生成しないようにする方法で、これができると前述した四つの平面に対してはクリップが全く必要なくなる。この方法は幅が事実上無限大のガードバンドを使うので、そのまま「無限ガードバンド (infinite guard-band)」と呼ばれる。二つ目の方法は三角形を実際にクリップする方法で、このときはラスタライザの計算がオーバーフローしない範囲に収まるようにクリップが行われる。例えば \(-32768 \leq X \leq 32767\), \(-32768 \leq Y \leq 32767\) を満たす整数座標 (大文字の \(X\) と \(Y\) はスクリーン空間の位置を表す。以下同様) を持つ三角形を扱えるだけの内部ビットをラスタライザが持つとする。このとき通常のビュー平面を使ったビューポートカリングテスト (つまり「この三角形は視錐台の外側にあるか？」の判定) を行う必要があるのは変わらないが、クリッピングで使うのはガードバンドのクリップ平面であり、このクリップ平面は射影変換とビューポート変換の後に座標が安全な範囲に収まるように取られる。そろそろ図を描こう:

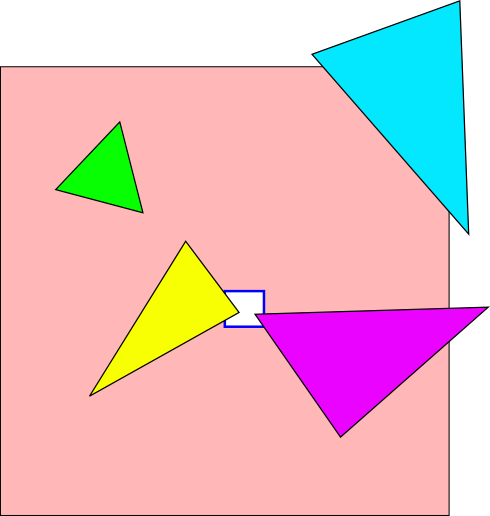
ガードバンドクリッピング
ガードバンドクリッピング

ほぼ中央にある白い四角形がビューポートを表し、それを囲む大きなピンク色の領域がガードバンドを表す。この画像だとビューポートがずいぶん小さく見えるが、実はこれでも見えなくならないように巨大なビューポートを選んでいる！ 今考えているガードバンドクリッピングの範囲は -32768 ... 32767 なので、このビューポートは幅と高さが約 5500 ピクセルということになる──そうだ、ここにある三角形はどれも非常に大きい :) 話を進めると、図中の三角形には重要なケースが示されている。緑色の三角形は全体がガードバンドに収まっているが、ビューポート領域の外側にあるので、ガードバンドクリッピングまで到達しない──ビューポートカリングで破棄される。青い三角形はガードバンド領域からはみ出ておりクリップが必要だが、これもビューポート領域の完全に外側にあるのでビューポートカリングで破棄される。そして紫色の三角形はビューポート内部とガードバンド外部の両方にまたがるので、この三角形はクリップする必要がある。

ここから分かるように、ガードバンドの四つの平面で本当にクリップしなければならない三角形というのは非常に極端なケースである。先ほど言ったように、めったに起きない──あまり気にしないことだ。

クリッピングを正しく行う

こういった点に驚くような部分はないはずだ。アルゴリズムさえ知っていれば、難しいとも思えないだろう。しかし悪魔は細部に宿る。必ずだ。実際のクリッピングにおいて三角形のクリップ処理が従う必要のある自明でない規則の一部を次に示す。これらの規則がどれか一つでも破られると、辺を共有して隣接する三角形の間に隙間ができるケースが生まれる。これは許されていない。

この煩わしい near 面と far 面

オーケー、これで四つの側面に対する簡単で高速な解決法が手に入った。では near 面と far 面についてはどうだろうか？ near 面は特に面倒になる。ビューポートから少しだけ外側にはみ出す三角形だけが残ったとき、クリッピングが最も多く行われるのは near 面だからだ。何ができるだろうか？ z ガードバンド？ しかしどうすれば上手く行くだろう──z 軸方向にラスタライズは起こらない！ そもそもピクセルの z 座標は三角形を補間して手に入る値じゃないか！ これじゃだめだ。

しかし逆に考えれば、z 座標は三角形に渡る補間によって計算される値に過ぎない。z-near テスト (\(Z < 0\)) は \(Z\) を補間で計算した後でならとても簡単に行える──符号ビットを見るだけだ (\(z\) ではなく \(Z\) なことに注意してほしい。\(Z\) は射影後の「スクリーン座標」を表す)。z-far テスト (\(Z > 1\)) には比較が一度必要になるが、そうだとしてもピクセルごとの Z 比較 (Z テスト！) はいずれ行うので、大きな負担にはならない。他にも考慮すべきことはあるが、こういった形の z クリッピングも忘れてはならない選択肢の一つである。もし NVIDIA の「depth clamp」という OpenGL 拡張機能をサポートしたいなら、z-near/z-far のクリッピングをスキップできる必要がある。実は私は、この拡張機能の存在は彼らのハードウェアが実際にスキップしている、あるいはかつてスキップしていたことを示す大きなヒントではないかと思っている。

これで通常のクリップ平面としては \(0 < w\) が一つ残るだけとなった。これも取り除けないだろうか？ 答えは「同次座標で動作するラスタライズアルゴリズム (例えばこれを参照) を使えばできる」だ。ただハードウェアがこれを使っているかどうか私には分からない。このアルゴリズムは簡単で美しいのだが、D3D11 の (非常に厳格な！) ラスタライズ規則に正確に従うのが難しいように思える。しかし私が気付いていない上手いトリックがあるのかもしれない。まぁともかく、クリッピングについてはこれで終わりだ。

射影変換とビューポート変換

射影は x, y, z 座標の値を受け取ってそれらを w 座標の値で割るだけである (同次ラスタライザを使っているときは射影を行わないのだが、これからこの可能性は無視する)。射影により各座標が -1 から 1 の正規化デバイス座標 (normalized device coordinate, NDC) が手に入る。その後ビューポート変換が適用され、射影された \(x\) と \(y\) はピクセル座標 (\(X\) と \(Y\) と呼ぶ) に、射影された \(z\) は \([0,1]\) 内の値 (\(Z\) と呼ぶ) に変換される。このとき z-near 面が \(Z=0\) であり、z-far 面が \(Z=1\) となる。

この段階で、各頂点はサブピクセルグリッド (ピクセルを等分割した格子) 上の分数座標にスナップされる。D3D11 では三角形の座標がちょうど 8 ビットのサブピクセル精度を持つことがハードウェアに要求される。このスナップによって一部の非常に細いとげのような三角形 (そのままだと問題が起こるもの) は退化し、レンダリングする必要がなくなる。

背面カリングなどのカリング

全ての頂点に対する \(X\) と \(Y\) が手に入ると、辺ベクトルの直積から三角形の符号付き面積を計算できる。この面積が負なら三角形の頂点は反時計回りに並んでおり、正なら時計回りに並んでいる (これは \(X\) と \(Y\) がピクセル座標であるためだ。D3D のピクセル空間は下向きが正なので、符号が逆転する)。面積がゼロなら三角形は退化しているので、安全にカリングできる。さらに、この時点で三角形の向きが判明するので、背面カリングも (有効化されていれば) 行える。

以上だ！ これでラスタライズの準備が (ほぼ...) 整った。実際にはまだ三角形セットアップをしなければならないが、これにはラスタライズがどう行われるかについての知識が多少必要となるので次章に回す。では、また会おう。

最後に

本章でも、省略した話題や単純化した話題がある。現実ではもっと複雑になっている部分に関していつも通り注意事項をここに示す。例えば先ほどは普通の同次クリッピングアルゴリズムを使えばそれで済むとした。たいていの場合、それで問題はない──しかし、頂点シェーダーのアトリビュートに対して透視的に正しい補間ではなくスクリーン空間に関して線形になるような補間を行うよう指示するフラグが存在する。一方で普通の同次クリッピングは必ず透視的に正しい補間を行う。つまりスクリーン空間に関して線形なアトリビュート補間が指定された場合は、追加の処理を行って透視的に正しくない値を計算しなければならない :)

この章ではプリミティブについて少し話をしたが、ほぼ三角形についてだけ話をした。点と直線は難しくないが、正直になろう、この二つのためにここに来たのではないはずだ。興味があるなら詳細を自分で考えてみてほしい :)

ラスタライズのアルゴリズムは大量にあり、中にはほとんどのクリップを飛ばせるもの (紹介した Olano の 2DH 法など) も存在する。ただ前述のように D3D11 が三角形ラスタライザに対して非常に厳密な要件を課しているので、ハードウェアの実装で好き勝手出来る余裕はあまりない。そういったアルゴリズムを仕様に完全に従うよう調整できるかどうか私は確かなことを知らない (次章で触れるように、細かな点が大量にある)。そこで本章および以降では、この点を綺麗に解決することはできないと仮定して話を進める。するとここでも、私が説明するあまり綺麗でないアプローチはラスタライザにおけるピクセルごとの計算がわずかに少ないので、ハードウェア実装でも有利である可能性がある。またもちろん、こういった問題を全て解決する魔法の妖精の粉をどこかで見落としているかもしれない。そういったことはグラフィックスで驚くほど頻繁に起きる。もし素晴らしい解決法を知っているなら、コメントで教えてほしい！

最後に、ここで説明した三角形のカリングは本当に最低限だ。例えばラスタライズで一つもピクセルを生成しない三角形の集合は、面積がゼロの三角形の集合よりもずっと大きい。この集合を十分高速に (あるいは十分少ないゲートで) 見つけられればすぐに破棄できるので、三角形セットアップに送る必要がなくなる。三角形セットアップと少なくともいくらかのラスタライズを行う前に安価にカリングを行える最後のチャンスがここであり、三角形を早期に破棄する方法を見つけることは非常に大きな価値を持つ。

広告
このページの文章はテキストゆれないくんを使って校正されました。