テッセレーション

おかえり！ この章で見ていくのは D3D11/シェーダーモデル 5.x 世代のハードウェアで導入された機能の中でおそらく "広告塔" 的なポジションにある機能、テッセレーションである。テッセレーションが興味深いのは、面白い話題である上に、ユーザーから見える大規模なコンポーネントが追加されてしかもそれがプログラム不可能というのは久しぶりであるためだ。

概念的にはとても簡単だったジオメトリシェーダー (頂点ではなく完全なプリミティブに対するシェーダーというだけだった) と異なり、「テッセレーション」というトピックはいくらかの説明を必要とする。ジオメトリをテッセレートする方法はいくらでもある──有名なものを挙げるだけでも、たくさんの亜種を持つスプラインパッチ、様々なサブディビジョンサーフェス、そしてディスプレースメントマッピングがある。つまり機能リストに「テッセレーション」と書いてあったとしても、 GPU が提供するサービスやその実装は全く明らかでない。

ハードウェアテッセレーションの動作の説明は、おそらく中央から始めるのが最も簡単だろう──実際のプリミティブテッセレーションステップと、そこで課される様々な要件である。新しいタイプのシェーダー (D3D11 のハルシェーダーとドメインシェーダー、OpenGL 4.0 のテッセレーション評価シェーダー) の説明は後に回す。

テッセレーション──想像とは少し違う

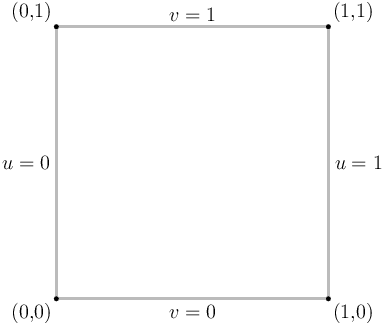
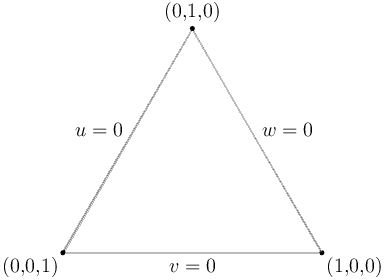
シェーダーモデル 5.x クラスのハードウェアが実装するテッセレーションは「パッチベース」と呼ばれる種類のテッセレーションである。CG の文献におけるパッチタイプの名前は普通、制御点からテッセレート後の点を構築するのに使われる関数の種類によって決まる (B-スプラインパッチ、ベジェ三角形など)。ただこういった話題は新しいタイプのシェーダーで処理されるので、ここでは触れない。GPU に含まれる実際の固定機能テッセレーションユニットは出力メッシュのトポロジー (言い換えれば、頂点がいくつあって、互いにどう接続するのか) だけを扱う。そしてこのユニットの視点に立つ限り、基本的にパッチには二つの種類しかない。一つはクアッドベースのパッチで、二つの直交する座標軸を持つ変数ドメインに定義される (ここでは二つのパラメータを \(u\), \(v\) と呼ぶことにする。どちらも \([0,1]\) に含まれる)。これは単一変数の基底関数二つのテンソル積を取ることで構築されることが多い。もう一つは三角形ベースのパッチで、こちらでは重心座標系をベースとした三つの座標 (\(u, v, w \geq 0\) と \(u + v + w = 1\) を満たす \(u, v, w\)) を使った冗長な表現が使われる。D3D11 の用語ではそれぞれ「quad」ドメインおよび「tri」ドメインと呼ばれる。二次元曲面ではなく一つ以上の一次元曲線を生成する「isoline」ドメインもこれらとは別に存在するが、私はこれを本シリーズにおける直線と点のプリミティブと同じように扱う。つまりその存在は示されるが、詳しく説明されることはない。

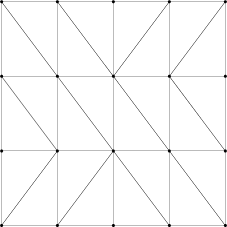
テッセレートされるプリミティブは対応するドメインの座標系で自然に図示できる。クアッドベースのパッチでは単位正方形を使ってドメインを描画するのが自然な選択なのでこれを使い、三角形ベースのパッチでは正三角形を使うことにする。この章で説明に使う座標系を次に示す。辺と頂点にはラベルを付けた:

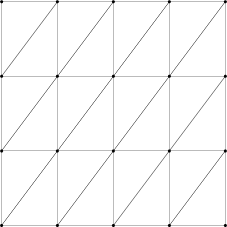
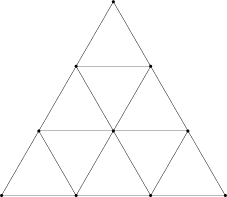
話を進めよう。クアッドと三角形には両方とも、私からすれば「自然」と言いたくなるようなテッセレートの方法がある。それを次の図に示すが、実はこのメッシュトポロジーが手に入ることはない:

同じレベルに対してテッセレータが実際に出力するメッシュを次に示す:

クアッドでは、ほぼ期待通りの分割が手に入る (対角線がいくつか反転しているが、すぐに触れる)。しかし三角形の方はまるで違う。これは上述の「自然な」ッセレーションからは大きく異なり、頂点の数さえ違う (10 ではなく 12 となっている)。何か面白いことが起こっているのは明らかだ──また明らかに、異なるテッセレーションレベル間の遷移がどう処理されるかについても説明が必要である。

つじつま合わせ

部屋にいる象はパッチ間の遷移処理である。単一の三角形 (あるいはクアッド) をテッセレートするのは簡単だが、テッセレーションの係数はパッチごとに指定できるのが望ましい。必要な三角形だけを生成したいからだ──メッシュの中で遠方にある部分に大量の (背面カリングされる可能性もある) 三角形を無駄に生成するのは避けたい。さらにテッセレーションの実行は高速に、さらに理想的には追加でメモリを使用せずに行いたい。これは準備のためのグローバルなポストパスの類が問題外であることを意味する。

解決法は──ハルシェーダーやドメインシェーダーを書いたことがあれば知っていると思うが──実際のテッセレーション処理を完全に純粋かつローカルにして、出来上がるメッシュに隙間が無い (watertight である) ことを保証する仕事をシェーダーに押し付けるというものだ。隙間の無い分割の計算は一つの完全なトピックであり、ドメインシェーダーのコードで細かな注意が必要な点の一つとなっている。ここではシェーダーにおけるテッセレーション表現の計算に関する詳細は飛ばして、基本的なことだけを説明する。各パッチが複数のテッセレーション係数 (tessellation factor, TF) を持つようにして、それをハルシェーダーで計算するというのが基本的なメカニズムである。TF はパッチ内部に一つか二つ、そして各辺に一つずつ割り振られる。パッチ内部の TF (内部 TF) は自由に選択できる。これに対して二つのパッチが辺を共有するときは、その辺の TF (辺 TF) は全く同じ値に計算されるようにしなければならず、そうしないと隙間が生まれる。ハードウェアはこの点を気にかけない──各パッチに対してただ個別に処理を行う。もし全てが上手く行けば、隙間の無い素敵なメッシュが手に入る。もしそうでなければ、それはあなたが解決すべき問題だ。ハードウェアが保証しなければならないのは隙間の無いメッシュの生成が (それなりの効率で) 行えることだけである。この点が厄介になる状況もある: 後述する。

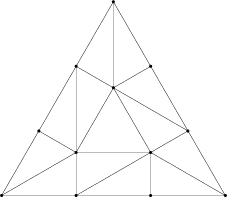
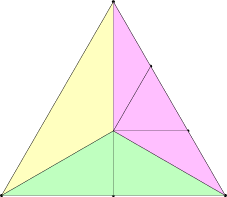
ここからの説明で使う新しい参照パッチを次に示す。今回は TF の働きが見やすくなるよう、各辺に異なる TF を割り当てている:

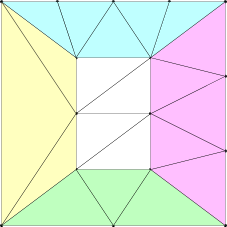
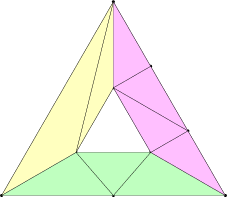
異なる辺 TF に影響される領域に異なる色を付けた。色の付いていない中心部分は内部 TF に影響を受ける。図中の辺 \(u=0\) (黄) の TF は 2 であり、辺 \(v=0\) (緑) の TF は 3、辺 \(u=1\) と \(w=0\) (ピンク) の TF は 4、辺 \(v=1\) (クアッドのみ、水色) の TF は 5 である──これらの値は対応する外側の辺に沿った頂点の個数とちょうど等しい。この二つの図から明らかなように、トポロジーの組み立てで基本単位となる操作は異なる個数の頂点が並んでいる分割後の二辺の間に辺を綺麗に縫い通す操作である。この操作の詳細は多少複雑である割に特に面白くないので、ここでは触れない。

内部 TF はクアッドでは非常に簡単になる: 上のクアッドは u 方向の内部 TF が 3 で、v 方向の内部 TF が 4 である。基本的にテッセレート後のジオメトリはそのサイズの構造格子で、例外的に最初と最後の行/列では向き合う辺上の頂点の間を縫い結んだジオメトリとなる (いずれかの辺 TF が 1 だと、u と v の両方に関する内部 TF が 2 であるかのような構造が最終的なメッシュとなる)。三角形では少し複雑になる。これまでに示してきたのは内部 TF \(N\) が奇数の場合で、このとき三角形の内側に \((N+1)/2\) 個の三角形が生成され、一番内側の図形は単一の三角形となる。\(N\) が偶数のときは内部に \(N/2\) 個の三角形と中心に一つの点が生成される。\(N = 2\) の場合を次に示す。このときは辺上の頂点と中心の頂点を縫い合わせただけとなる:

最後に、クアッドを三角形に分割するとき対角線はパッチの中心から (ドメイン座標空間で) 遠ざかる方向になるように選ばれ、引き分けの解消には一貫した規則が使われる。これは最終的なメッシュで回転対称性を最大化するためである──自由度が存在するなら、残した方がよさそうだ！

非整数テッセレーションと全体のパイプラインフロー

ここまでは整数の TF についてだけ話をしてきた。いわゆる「分割タイプ」が「integer」または「pow2」のときは、テッセレータに整数の TF だけを渡すことができる。整数でない (分割タイプが pow2 なら 2 のべきでない) TF をハルシェーダーが生成すると、それは次の有効な値に丸められる。これより興味深いのが残りの二つの分割タイプ「fractional-odd」と「fractional-even」である。これらの分割タイプを使うと、TF を増加させたとき整数に対応するメッシュから次の整数に対応するメッシュへ一気に飛ぶ (そして目に見えるポッピングが生じる) のではなく、新しい頂点がメッシュ上の既存の頂点と同じ位置から始まって TF が増加するのに従って新しい位置へと移動するようになる。

例えば fractional-odd のテッセレーションで内部 TF を 3.001 に設定すると、生成されるメッシュの見た目は内部 TF が 3 の場合とほとんど変わらない──しかしトポロジー的には内部 TF が 5 の場合と同じになる。つまり同じ中心を持つ三つの三角形が存在している (ただし最も内側の三角形は非常に小さい)。その後内部 TF が 5 になるまで中心の三角形は大きくなり、5 のとき最終的な位置となる。内部 TF が 5 より大きくなるとメッシュはトポロジー的に内部 TF が 7 の場合のメッシュと同様になるが、ここでもほぼ縮退した三角形が中心に生じる。以降同様であり、fractional-even では偶数の TF に対して同じことが行われる。

テッセレータの出力は二つの要素からなる: テッセレートされた頂点の (ドメイン座標における) 位置と、対応する隣接情報 (基本的にはインデックスバッファ) である。

以上で固定機能テッセレータユニットの基本的な動作が説明できたので、次は一歩後ろに下がって、テッセレータでプリミティブを大量生産するためにすべきことを見ていく: まず、パッチを構成する入力制御点をひとまとめにしてハルシェーダー (HS) に入力する必要がある。これを受けて HS は制御点と「パッチ定数」(この二つはドメインシェーダーに渡される)、およびテッセレーション係数 (これも実質的にはただのパッチ定数) を計算する。それから固定機能テッセレータが実行されてドメイン位置と関連するインデックスが生成され、ドメイン位置のそれぞれに対してドメインシェーダー (DS) が実行される。DS の実行が終わるともう一度プリミティブアセンブリが行われ、組み立てられたプリミティブは GS パイプライン (GS が有効なとき) もしくはビューポート変換/クリッピング/カリング (それ以外のとき) に送られる。

では HS ステージを簡単に見てみよう。

ハルシェーダーの実行

ジオメトリシェーダーと同様に、ハルシェーダーは完全な (パッチ) プリミティブを入力として動作する──入力のバッファ処理がもたらす頭痛も一緒にやって来る。頭痛のひどさは入力のパッチの種類によって大きく異なる。例えばパッチが三次ベジェパッチだと、4x4 = 16 個の点がパッチごとに必要になり、そこからはクアッドが一つ出力されるだけかもしれない (カリングされて全く出力されない可能性もある)。相当な量のデータを処理しなければならないのは明らかであり、効率的なシェーディングは行えない。一方でテッセレーションが通常の三角形を入力に取る場合 (たいていの人が行う処理) には入力のバッファ処理はたいしたことがないので、何らかの問題やボトルネックを引き起こす可能性は低い。

さらに重要なこととして、全てのプリミティブに対して実行されるジオメトリシェーダーとは異なり、ハルシェーダーはそれほど頻繁に実行されるわけではない──実行はパッチごとに一度だけである。実際のテッセレーション処理が少しでも (TF があまり大きくなくても) 行われる限り、ハルシェーダーに入力されるパッチの個数は出力される三角形の個数よりはるかに小さくなる。言い換えれば、HS の入力が少しぐらい非効率であったとしても、ただ多く実行されないという理由で、GS の場合と比べるとあまり問題にならない。

ハルシェーダーが持つもう一つの素敵な特徴が、ジオメトリシェーダーと異なり、出力データの量が可変でないことだ。HS が出力するのは固定された個数の制御点と固定された量のパッチ定数であり、制御点にはそれぞれ固定された個数のアトリビュートが関連付く。これらの情報は全てコンパイル時に判明するので、実行時に動的なバッファ管理が必要ない。ハルシェーダーが一度に 16 個のハルシェーディングを行うなら、各ハルが出力するデータがどこに収まるかは実行を始める前に分かる。これはジオメトリシェーダーと比べたとき確実に有利な点である。ジオメトリシェーダーでは多く場合で (例えば emit/cut 命令に至る制御フローがコンパイル時に静的に評価できたとき) 出力される頂点の個数を静的に知ることができ、さらに全ての場合で出力される頂点の最大個数には保証が付いていた。しかし HS では出力データの量が一定であることが必ず保証されるので、追加の解析が必要にならない。要するにバッファ管理の問題は基本的に存在しない。ただ一つだけ、ここでもプリミティブのタイプによっては大きな出力バッファが必要になって (メモリ/レジスタの制約により) 達成できる並列性が制限される可能性がある。

最後に、D3D11 のハルシェーダーはコンパイル方法が特別になっている。他の種類のシェーダーはどれも一つのコードブロック (にサブルーチンが付いたもの) として構成されるが、ハルシェーダーは複数のフェーズからなっており、各フェーズが複数の (独立した) 実行スレッドを持つ。この詳細は主にドライバとシェーダーコンパイラを書くプログラマーが気にすることだが、一つ言っておくなら、平均的な HS が大きな潜在的並列性を持った状態でパッケージされるようになっている。ジオメトリシェーダーを苦しめるボトルネックを避けようとマイクロソフトが非常に熱心なのは間違いない。

まとめると、ハルシェーダーはパッチごとに出力を生成する。出力の大部分は対応するドメインシェーダーが実行するまで取っておかれるが、唯一 TF だけはテッセレータユニットに送られる。いずれかの TF がゼロ以下 (あるいは NaN) だと、そのパッチはカリングされて対応する制御点とパッチ定数は静かに捨てられる。そうでなければテッセレータ (上述の機能を実装する専用ユニット) が起動して、ちょうど今シェーディングされたパッチを読み、ドメイン点の位置と三角形のインデックスを大量生産する。次はドメインシェーダーを実行する準備を整える必要がある。

ドメインシェーダー

はるか昔に説明した頂点シェーディングと同様に、複数のドメイン頂点を集めて一つのバッチとしてシェーディングして PA に渡す処理を行いたい。固定関数テッセレータはこれを行える: 頂点の位置とインデックスを生成するついでに処理する "だけ" で済む (引用符で囲ったのは、入出力の管理が多少必要なためだ)。

入力と出力に関して言えば、実はドメインシェーダーは非常に単純である: 頂点ごとに変化する唯一の入力はドメイン点の u 座標と v 座標だけであり (w 座標が使われる場合でも、テッセレータによる計算や受け渡しは必要ない: \(u + v + w = 1\) が成り立つので、\(w = 1 - u - v\) と計算できる)、他の値はパッチ定数あるいは制御点 (この二つはパッチ単位で同じ値となる)、そうでなければ定数バッファである。また出力は頂点シェーダーと基本的に同じになる。

要するに、DS まで来れば後は簡単になる。DS のデータフローは VS のものと同じくらい簡単であり、このパスなら効率的な実行方法も知られている。これはおそらくジオメトリシェーダーと比べたときに D3D11 のテッセレーションパイプラインが最も優れる点と言える: 実際の三角形の増幅処理がシェーダーで起こらないために貴重な ALU サイクルは無駄にならず、さらに最悪のケースで見込まれる頂点数に対応するためのバッファ空間を保持する必要もない。増幅処理はローカルなコンポーネント (テッセレータ) で行われ、これは基本的にステートマシンであり、入力は TF が数個と非常に少なく、非常にコンパクトな出力 (事実上インデックスバッファと出力頂点ごとに二次元座標が一つ) を生成する。このためバッファ用のメモリはずっと少なくて済み、シェーダーユニットを入出力の管理ではなく実際のシェーディングで忙しくさせることができる。

本章は以上となる──次章ではコンピュートシェーダーについて話をする。私が最初に書いたアウトラインでは次が最終章だ！ それでは。

後書き

いつも通り、いくつか注意事項がある。「isoline」というパッチタイプもあるが、これについては一切説明をしなかった (もし需要があれば書くこともできる)。テッセレータには対称性と正確性に関する様々な要件が課される。生成される頂点のドメイン位置に関して D3D11 の仕様は非常に細かく定めているので、異なるハードウェアベンダーでもビット単位で正確な結果が手に入ると期待して基本的に構わない。意図的に定められていないのは頂点あるいは三角形が生成される順序であり、実装は一貫している限り (同じ入力が必ず同じ順序で出力を生成する限り) 好きなことをして構わない。テッセレータには細かい制約も多くある──例えばテッセレータが書き込むドメイン位置について、\(u, v, 1-u, 1-v\) は全て浮動小数点数として正確に表現できなければならない。こういった様々な条件はドメインシェーダーが隙間の無いメッシュを生成するための必要条件である。特に、単一の辺 AB が二つのパッチで共有されるとき、その辺 (一つのパッチでは辺 AB となり、もう一方では辺 BA としてテッセレートされる) が両方のパッチで同じようにテッセレートされるために重要となる。

隙間が生じないようにドメインシェーダーを書くのは難しく、細心の注意を必要とする。このシリーズの範囲からは外れるので、説明では意図的にこの話題を避けた。また私が飛ばしたもう一つの明らかな問題に、テッセレータによって生成される三角形のワインディングオーダーの問題がある (答え: アプリケーションから決められる──時計回りと反時計回りが両方サポートされる)。

HS と DS の入出力バッファリングは簡単にしか説明しなかったが、このバッファリングはこれまでに見てきたステージと非常に似ているので、文章を短くするのを優先して冗長な文章を避けた。説明が速すぎると感じたなら、頂点シェーダーとジオメトリシェーダーの章を読み直してほしい。

最後に、テッセレーションパイプラインは GS へ接続できるので、隣接情報を生成できるべきかどうかという疑問がある。パッチの "内側" では隣接情報を考えることができる (テッセレータユニットが書き込むインデックスが増えるだけだ) が、パッチの辺を考えると上手く行かなくなる。パッチをまたいだ隣接情報を考えるにはメッシュをグローバルに "認識" する必要があるのだが、これはテッセレータパイプラインが避けようとあれほど努力していたことである。よって、短くまとめると、NO だ。テッセレータは GS 用の隣接情報を生成せず、飾りのない三角形だけを生成する。