6.5. グラフの彩色多項式
グラフの彩色に関して驚くべき事実がもう一つある: 多重グラフ \(G\) が持つ適切な \(k\)-彩色の個数は \(k\) の多項式となる。正確に言えば次の通りである:
\(G=\left( V,E,\varphi\right) \) を多重グラフとする。\(x\) だけを不定元に持つ整数係数多項式 \(\chi_{G}\) を、次のように定める:
このとき、任意の \(k\in\mathbb{N}\) に対して次の等式が成り立つ:
これはおそらくグラフ理論ではなく組合せ論の教科書で紹介されるべき定理だろう。ただ、せっかくなので証明しておく (飛ばしても構わない)。次に示す証明は 1930 年に Hassler Whitney が [Whitney32, § 6] で示したものと本質的に同じである (単純グラフではなく多重グラフを扱うために必要となった変更が数か所ある)。
この証明では Iverson の括弧記法を利用する:
論理命題 \(\mathcal{A}\) に対して、Iverson の括弧記法 (Iverson bracket notation) \(\left[ \mathcal{A}\right]\) を次のように定義する:
例えば \(\left[ 2+2=4 \right] = 1\) や \(\left[2+2=5 \right] =0\) が成り立つ。
続いて、次の組合せ論的な等式 [17s, Lemma 3.3.5] を思い出しておく:
有限集合 \(P\) に対して、次の等式が成り立つ:
ここで \(\displaystyle \sum_{\substack{A\subseteq P}}\) は「\(P\) の全ての部分集合 \(A\) にわたる和」を意味する。
最後に、彩色に関する記法を一つ定める:
\(G=\left( V,E,\varphi\right) \) を多重グラフ、\(k\) を自然数、\(f\colon V\rightarrow\left\{ 1,2,\ldots ,k\right\} \) を \(G\) の \(k\)-彩色とする。\(E\) の部分集合 \(E_{f}\) を次のように定める:
\(E_{f}\) の要素を \(G\) の \(f\)-単色辺 (\(f\)-monochromatic edge) 辺と呼ぶ。
\(G=\left( V,E,\varphi\right) \) を次の多重グラフとする:
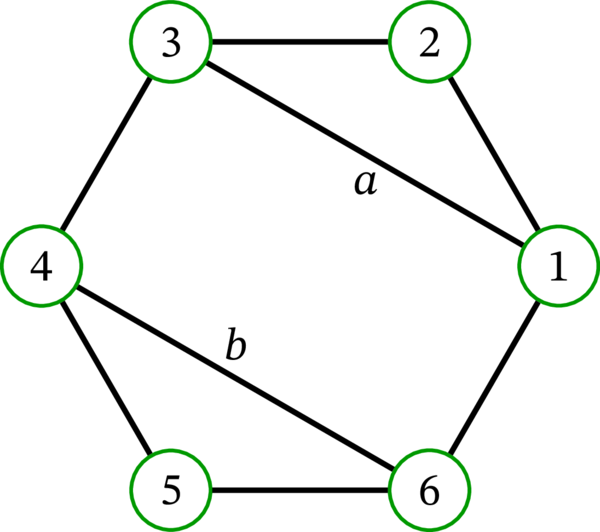
偶数の頂点を \(1\) に、奇数の頂点を \(2\) に移す \(G\) の \(2\)-彩色を \(f\colon V\rightarrow\left\{ 1,2\right\} \) とする (「奇数の頂点」とは整数として奇数である頂点を意味する。つまり \(1\), \(3\), \(5\) が奇数の頂点である。「偶数の頂点」も同様に定義される)。このとき \(E_{f}=\left\{ a,b\right\} \) が成り立つ。
次の事実は容易に分かる:
\(G=\left( V,E,\varphi\right) \) を単純グラフ、\(k\) を自然数、\(f\colon V\rightarrow\left\{ 1,2,\ldots ,k\right\} \) を \(G\) の \(k\)-彩色とする。このとき \(k\)-彩色 \(f\) が適切なのは \(E_{f}=\varnothing\) のとき、かつそのときに限る。
次の同値関係が分かる:
以上で命題 6.5.6 は証明された。□
\(G=\left( V,E,\varphi\right) \) を多重グラフ、\(B\) を \(E\) の部分集合、\(k\) を自然数とする。このとき、\(B\subseteq E_{f}\) を満たす \(G\) の \(k\)-彩色 \(f\colon V\rightarrow\left\{ 1,2,\ldots,k\right\} \) の個数は \(k^{\operatorname{conn}\left( V,\,B,\,\varphi |_{B}\right) }\) である。
\(V\) の非空部分集合 \(C\) と \(G\) の \(k\)-彩色 \(f\colon V\rightarrow\left\{ 1,2,\ldots,k\right\} \) に対して、制限 \(f|_{C}\) が定数写像である (全ての \(c \in C\) に対して \(f\left( c\right) \) が同じ) とき、\(f\) は \(C\) 上で定数 (constant) と言うことにする。これから次の命題を示す:
[Claim 1 の証明: これは「...が成り立つのは...のとき、かつそのときに限る」の形をした命題である。これから \(\Longrightarrow\) 方向と \(\Longleftarrow \) 方向を別々に証明する。
\(\Longrightarrow\): \(B \subseteq E_{f}\) と仮定する。この上で多重グラフ \(\left( V,B,\varphi\mid _{B}\right) \) の各成分上で \(f\) が定数だと示せばよい。
\(\left( V,B,\varphi|_{B}\right) \) の成分を任意に取って \(C\) とする。\(C\) 上で \(f\) が定数だと示す必要がある。言い換えれば、任意の \(c, d \in C\) に対して \(f\left( c\right) =f\left( d\right) \) を示したい。
\(c,d\in C\) を任意に取って固定する。このとき \(c\) と \(d\) は多重グラフ \(\left( V,B,\varphi|_{B}\right) \) の同じ成分 \(C\) に属するから、このグラフで \(c\) と \(d\) は路連結である。言い換えれば、多重グラフ \(\left( V,B,\varphi|_{B}\right) \) は \(c\) から \(d\) への路を持つ。この路を
とする。このとき \(v_{0}=c\) と \(v_{s}=d\) と \(e_{1},e_{2},\ldots,e_{s}\in B\) が成り立つ。
任意に \(i\in\left\{ 1,2,\ldots,s\right\} \) を取る。辺 \(e_{i}\) は端点に \(v_{i-1}\) と \(v_{i}\) を持つ。一方 \(e_{1},e_{2},\ldots ,e_{s}\in B\) より \(e_{i}\in B\subseteq E_{f}\) が分かるので、\(f\) は \(e_{i}\) の両端点に同じ色を割り当てる (\(E_{f}\) の定義より)。言い換えれば \(f\left( v_{i-1}\right) =f\left( v_{i}\right) \) が成り立つ。
\(i\) を固定したことを忘れる。以上で任意の \(i\in\left\{ 1,2,\ldots,s\right\} \) に対する等式 \(f\left( v_{i-1}\right) =f\left( v_{i}\right) \) が示せた。等式を全て合わせれば次を得る:
よって \(f\left( v_{0}\right) =f\left( v_{s}\right) \) である。\(v_{0}=c\) および \(v_{s}=d\) なので、\(f\left( c\right) =f\left( d\right) \) が分かる。
\(c\) と \(d\) を固定したことを忘れる。以上で任意の \(c,d \in C\) に対して \(f\left( c\right) =f\left( d\right) \) が証明できた。言い換えれば、\(C\) 上で \(f\) は定数である。\(C\) は多重グラフ \(\left( V,B,\varphi|_{B}\right) \) の任意の成分だったから、多重グラフ \(\left( V,B,\varphi|_{B}\right) \) の各成分上で \(f\) は定数だと結論できる。以上で Claim 1 の \(\Longrightarrow\) 方向は証明された。
\(\Longleftarrow\): 多重グラフ \(\left( V,B,\varphi|_{B}\right) \) の各成分上で \(f\) が定数だと仮定する。この上で \(B\subseteq E_{f}\) を示せばよい。
\(e \in B\) を任意に取り、\(e\) の端点を \(u\), \(v\) とする。このとき \(\left( u,e,v\right) \) は多重グラフ \(\left( V,B,\varphi|_{B}\right) \) における \(u\) から \(v\) への歩道である (\(e \in B\) より)。よって、このグラフで \(u\) は \(v\) と路連結である。つまり \(u\) と \(v\) は多重グラフ \(\left( V,B,\varphi|_{B}\right) \) の同じ成分に属する。このグラフの各成分上で \(f\) が定数という仮定より、\(f\left( u\right) =f\left( v\right) \) が分かる。\(e\) は \(u\) と \(v\) を端点に持つので、彩色 \(f\) で \(e\) の両端点は同じ色を持つ。これと \(e\in B\subseteq E\) から \(e \in E_{f}\) だと結論できる (\(E_{f}\) の定義より)。
\(e\) を固定したことを忘れる。以上で任意の \(e\in B\) で \(e\in E_{f}\) だと示せた。言い換えれば \(B\subseteq E_{f}\) である。よって Claim 1 の \(\Longleftarrow\) 方向は証明された。これで Claim 1 の証明が完了した。]
Claim 1 からは、\(B \subseteq E_{f}\) を満たす \(k\)-彩色 \(f\colon V\rightarrow\left\{ 1,2,\ldots,k\right\} \) が、多重グラフ \(\left( V,B,\varphi|_{B}\right) \) の各成分上で定数である \(k\)-彩色 \(f\colon V\rightarrow\left\{ 1,2,\ldots,k\right\} \) に等しいことが分かる。よって、そういった \(k\)-彩色 \(f\) は次の手続きで構築できる:
-
多重グラフ \(\left( V,B,\varphi |_{B}\right) \) のそれぞれの成分 \(C\) に対して色 \(c_{C} \in \left\{ 1,2,\ldots,k\right\}\) を選択し、\(C\) に属する頂点に色 \(c_{C}\) を割り当てる (つまり、任意の \(v\in C\) に対して \(f\left( v\right) =c_{C}\) と定める)。
この手続きにおいて、多重グラフ \(\left( V,B,\varphi|_{B}\right) \) の各成分に対応する色は自由に選択できる。多重グラフ \(\left( V,B,\varphi|_{B}\right) \) 成分は \(\operatorname{conn}\left( V,B,\varphi|_{B}\right) \) 個あり、選択できる色は \(k\) 個ある。よって全部で \(k^{\operatorname{conn}\left( V,\,B,\,\varphi|_{B}\right) }\) 個の選択肢がある。それぞれの選択肢が異なる \(k\)-彩色 \(f\colon V\rightarrow\left\{ 1,2,\ldots,k\right\} \) を与えるので、\(B\subseteq E_{f}\) を満たす \(f\)-彩色 \(f\colon V\rightarrow\left\{ 1,2,\ldots,k\right\} \) の個数は \(k^{\operatorname{conn}\left( V,\,B,\,\varphi|_{B}\right) }\) だと分かる。以上で補題 6.5.7 は証明された。□
\(\left( V,E,\varphi\right) \) を多重グラフ、\(F\) を \(E\) の部分集合、\(k\) を自然数とする。このとき次の等式が成り立つ:
次の等式が分かる:
よって 系 6.5.8 は証明された。□
まず、次の等式が容易に分かる:
なぜなら、\(G\) の全域部分グラフは何らかの \(F \subseteq E\) に対する \(\left( V,F,\varphi|_{F}\right) \) の形をした部分グラフに等しいからである。
\(k\) を自然数とする。\(\left(\text{\# } G \text{ の適切な } k \text{-彩色}\right) =\chi_{G}\left( k\right) \) を示せばよい。
等式
で \(x\) を \(k\) に置き換えると、次を得る:
つまり、\(G\) の適切な \(k\)-彩色の個数は \(\chi_{G}\left( k\right) \) である。以上で定理 6.5.1 は証明された。□
定理 6.5.1 の多項式 \(\chi_{G}\) を \(G\) の彩色多項式 (chromatic polynomial) と呼ぶ。
グラフの彩色多項式の例をいくつか示す:
\(n \geq 1\) を整数とする。
-
\(n\) 個の頂点を持つ路グラフ \(P_{n}\) に対して次の等式が成り立つ:
\[ \chi_{P_{n}}=x\left( x-1\right) ^{n-1} \] -
より一般的には、\(n\) 個の頂点を持つ木 \(T\) に対して次の等式が成り立つ:
\[ \chi_{T}=x\left( x-1\right) ^{n-1} \] -
\(n\) 個の頂点を持つ完全グラフ \(K_{n}\) に対して次の等式が成り立つ:
\[ \chi_{K_{n}}=x\left( x-1\right) \left( x-2\right) \cdots\left(x-n+1\right) \] -
\(n\) 個の頂点を持つ空グラフ \(E_{n}\) に対して次の等式が成り立つ:
\[ \chi_{E_{n}}=x^{n} \] -
\(n \geq 2\) と仮定する。\(n\) 個の頂点を持つ閉路グラフ \(C_{n}\) に対して次の等式が成り立つ:
\[ \chi_{C_{n}}=\left( x-1\right) ^{n}+\left( -1\right) ^{n}\left(x-1\right) \]
(c): 多項式等価性の永続原理 (定理 5.19.4) より、二つの実数係数多項式が等しいと示すには任意の非負整数で両者が等しいと示せば十分である。よって任意の \(k \in \mathbb{N}\) で \(\chi_{K_{n}}\left( k\right) =k\left( k-1\right) \left( k-2\right) \cdots\left( k-n+1\right) \) だと示せれば \(\chi_{K_{n}}=x\left( x-1\right) \left( x-2\right) \cdots\left( x-n+1\right) \) を証明できたことになる。
これを証明しよう。\(k \in \mathbb{N}\) を任意に取って固定する。定理 6.5.1 を \(G = K_{n}\) に適用すれば、次の等式を得る:
\(K_{n}\) の適切な \(k\)-彩色はいくつあるだろうか? そういった \(k\)-彩色は全て次のアルゴリズムで構築できる:
-
まず、頂点 \(1\) の色を選ぶ。色の選択肢は \(k\) 個ある。
-
次に、頂点 \(2\) の色を選ぶ。頂点 \(2\) は頂点 \(1\) と隣接するので、両者の色は同じであってはいけない。よって頂点 \(2\) の色の選択肢は \(k-1\) 個ある。
-
次に、頂点 \(3\) の色を選ぶ。頂点 \(3\) は頂点 \(1\) と頂点 \(2\) に隣接するので、これら二つの頂点と同じ色を持つことはできない。よって頂点 \(3\) の色の選択肢は \(k-2\) 個ある (頂点 \(1\) の色と頂点 \(2\) の色は異なるので、選択肢の個数は \(k\) から \(2\) だけ減る)。
-
以下同様に \(n\) 個の頂点全てに色を塗る。
こうして構築できる \(K_{n}\) の適切な \(k\)-彩色は全部で \(k\left( k-1\right) \left( k-2\right) \cdots\left( k-n+1\right) \) 個ある。よって次の等式を得る:
これと等式 \((2)\) より \(\chi_{K_{n}}\left( k\right) =k\left( k-1\right) \left( k-2\right) \cdots\left( k-n+1\right) \) を得る。以上で命題 6.5.10 (c) は証明された。
(d): 証明は (c) と同様であり、(c) より易しい。読者に任せる。\(\chi_{E_{n}}\) の定義 (定理 6.5.1) を使っても簡単に示せる。\(E_{n}\) の全域木は一つしか (\(E_{n}\) 自身しか) 存在しない。
(b):
\(n\) に関する数学的帰納法で示す。\(n=1\) なら、等式の正しさは容易に確かめられる。\(n > 1\) なら、定理 5.3.2 (a) より木 \(T\) は少なくとも一つの葉を持つ。\(T\) の葉を任意に取って \(\ell\) とする。このとき定理 5.3.3 よりグラフ \(T \setminus \ell\) は木である。\(T \setminus \ell\) は \(n-1\) 個の頂点を持つ木だから、その彩色多項式は \(\chi_{T\setminus\ell }=x\left( x-1\right) ^{n-2}\) だと帰納法の仮定から分かる。一方、任意の \(k \in \mathbb{N}\) に対して、\(T \setminus \ell\) の適切な \(k\)-彩色を最初に選び、最後に葉 \(\ell\) の色を選ぶことで \(T\) の適切な \(k\)-彩色を構築できる。このとき \(\ell\) は葉より次数が \(1\) なので、\(\ell\) の色の選択肢は \(k-1\) 個ある。よって、任意の \(k \in \mathbb{N}\) に対して次の等式が成り立つ:
定理 6.5.1 の設定を使えば、この等式は次のように書き換えられる:
この等式が任意の \(k \in \mathbb{N}\) に対して成り立つので、次を得る:
以上で再帰ステップが完了した。
命題 6.5.10 (b) も \(\chi_{T}\) の定義から導くことができる。\(T\) の全域部分グラフ \(H\) は閉路を持たないので、系 5.1.7 より \(\operatorname*{conn}H=n-\left\vert \operatorname*{E}\left( H\right) \right\vert \) が成り立つ事実を利用する。
(a): \(P_{n}\) は \(n\) 個の頂点を持つ木なので、この命題は (b) の特殊ケースである。
(e): いくつかの証明が知られている: [LeeShi19] には四つの証明が示されている。おそらく最も簡単なのは \(n\) に関する数学的帰納法を使う次の証明である: \(n \geq 2\) とする。\( k \in \mathbb{N}\) を任意に取って固定する。\(C_{n}\) の適切な \(k\)-彩色は、\(P_{n}\) の適切な \(k\)-彩色であって頂点 \(1\) と頂点 \(n\) に異なる色を割り当てるものに等しい。よって次の等式が分かる:
定理 6.5.1 の設定を使えば、この等式は次のように書き換えられる:
この等式が任意の \(k \in \mathbb{N}\) に対して成り立つから、次の等式が分かる:
この簡単な再帰方程式を \(\chi_{C_{n}}\) について解けば (e) が証明される。□
\(g\) を自然数とする。単純グラフ \(G\) を次のように定める。\(G\) の頂点は \(2g + 1\) 個の整数 \(-g,\ -g+1,\ \ldots,\ g-1,\ g\) であり、\(G\) の辺は次の通りである:
\(G\) の彩色多項式 \(\chi_{G}\) を求めよ。
[例: \(g=4\) のとき \(G\) は次のグラフとなる:
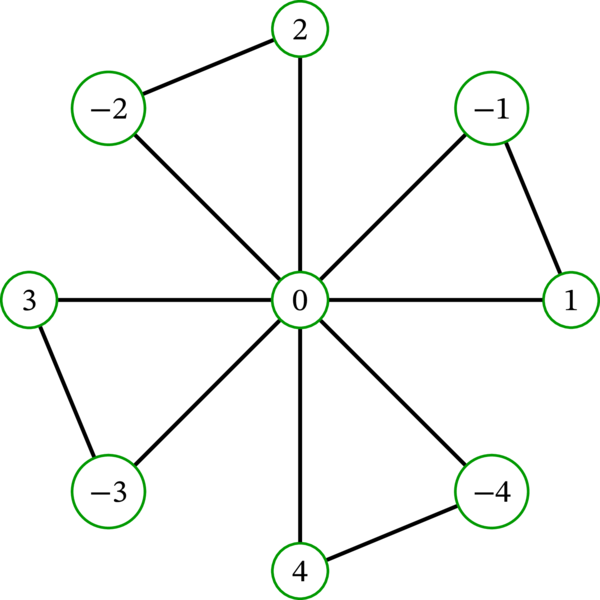
このグラフは \(2g+1 = 9\) 個の頂点と \(3g = 12\) 個の辺を持つ。]