8.6. 正則二分グラフ

Hall の結婚定理 (定理 8.3.4) は任意の二部グラフに \(X\)-完全なマッチングが存在するかどうかを判定する必要十分条件を与える。正則二部グラフ (全ての頂点が同じ次数を持つ二部グラフ) を考えるとき、この十分条件はより単純になる: \(X\)-完全なマッチングは常に存在する！本節では、この意外な事実を証明する (Hall の結婚定理を使えば難しくない)。そのために、まずは正則なグラフという概念を定義する:

定義 8.6.1

\(k\) を自然数とする。多重グラフ \(G\) の全ての頂点が次数 \(k\) を持つとき、\(G\) は \(k\)-正則 (\(k\)-regular) と言う。

例 8.6.2

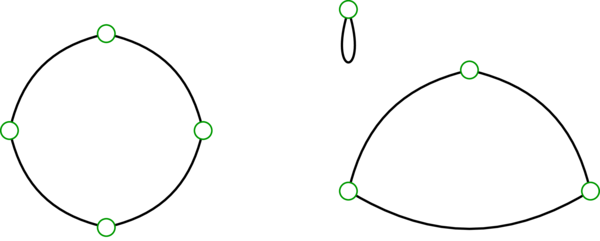
\(1\)-正則なグラフは辺集合全体が完全なマッチングとなるようなグラフである。言い換えれば、\(1\)-正則なグラフは \(2\) 次の路グラフ \(P_{2}\) の非交和として表せる。\(1\)-正則なグラフの例を示す:

例 8.6.3

\(2\)-正則なグラフは閉路グラフの非交和として表せる。\(2\)-正則なグラフの例を示す:

[\(C_{1}\) や \(C_{2}\) があっても \(2\)-正則となる。]

例 8.6.4

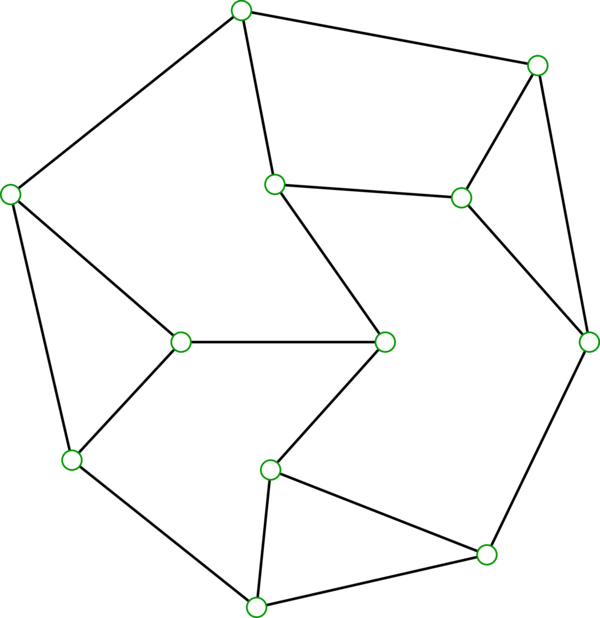
\(3\)-正則なグラフは立方体グラフ (cubic graph) あるいは三価グラフ (trivalent graph) と呼ばれる。そのようなグラフの例として Petersen グラフ (第 2.6.3 項) がある。次に示す Frucht グラフ (Frucht graph) も \(3\)-正則なグラフである:

Wikipedia には他にも例が多く載っている。全てを紹介することはとてもできない。

第 2.6.3 項で定義した Kneser グラフは全て正則となる:

例 8.6.5

任意の Kneser グラフ \(K_{S,k}\) は \(\dbinom{\left\vert S\right\vert -k}{k}\)-正則である。

[証明] Kneser グラフの定義より、この命題は「有限集合 \(S\) の任意の \(k\) 要素部分集合 \(A\) に対して、\(A\) と共通要素を持たない \(S\) の \(k\) 要素部分集合は \(\dbinom{\left\vert S\right\vert -k}{k}\) 個存在する」という命題に等しい。この命題は明らかである: \(A\) と共通要素を持たない \(S\) の \(k\) 要素部分集合は集合 \(S\setminus A\) の \(k\) 要素部分集合に等しく、\(S\setminus A\) は \( \left\vert S\right\vert -k \) 個の要素を持つ。□

命題 8.6.6

\(k > 0\) を正整数、\(\left( G,X,Y\right) \) を \(k\)-正則な二部グラフ (\(G\) が \(k\)-正則な二部グラフ) とする。このとき \(\left\vert X\right\vert =\left\vert Y\right\vert \) が成り立つ。

[証明] 多重グラフ \(G\) を \(G=\left( V,E,\varphi\right) \) と書く。\(\left( G,X,Y\right) \) は二部グラフより、任意の辺 \(e \in E\) は \(X\) に属する端点を唯一つ持つ。よって次の等式が成り立つ:

\[ \begin{aligned} \left\vert E\right\vert & = \sum_{x\in X}\underbrace{\left(\text{\# } x \text{ を含む辺} \right) }_{=\,\deg x}\\ & = \sum_{x\in X}\underbrace{\deg x}_{\substack{=k\\ (\because\ G \text{ は }k\text{-正則})}}\\ & = \sum_{x\in X}k \\ & = k\cdot\left\vert X\right\vert \end{aligned} \]

同様に \(\left\vert E\right\vert =k\cdot\left\vert Y\right\vert \) も示せる。よって \(k\cdot\left\vert X\right\vert =k\cdot\left\vert Y\right\vert \) が分かる。\(k > 0\) より両辺を \(k\) で割ることができるので、\(\left\vert X\right\vert =\left\vert Y\right\vert \) を得る。□

定理 8.6.7

[Frobenius のマッチング定理 (Frobenius matching theorem)] \(k\) を正整数、\(\left( G,X,Y\right) \) を \(k\)-正則な二部グラフ (\(G\) が \(k\)-正則な二部グラフ) とする。このとき \(G\) は完全マッチングを持つ。

[証明] まず、\(X\) の任意の部分集合 \(A\) が \(\left\vert N\left( A\right) \right\vert \geq\left\vert A\right\vert \) を満たすことを示す。

\(X\) の部分集合を任意に取って \(A\) とする。\(A\) に属する端点を持つ \(G\) の辺を考える。そういった辺を \(A\)-辺 (\(A\)-edge) と呼ぶことにする。\(A\)-辺はいくつあるだろうか？

\(\left( G,X,Y\right) \) が二部グラフで \(A \subseteq X\) なので、任意の \(A\)-辺は \(A\) に属する頂点を唯一つ含む。よって次の等式が成り立つ:

\[ \begin{aligned} \left(\text{\# } A \text{-辺}\right) & =\sum_{x\in A}\underbrace{\left(\text{\# } \text{頂点 } x \text{ を含む } A \text{-辺}\right) }_{\substack{=\,\deg x\\[3pt](\because\ A \text{-辺の定義})}}\\[30pt] & = \sum_{x\in A}\underbrace{\deg x}_{\substack{=\,k\\[3pt](\because\ G \text{ は } k \text{-正則})}} \\ & = \sum_{x\in A}k\\ & = k\cdot\left\vert A\right\vert \end{aligned} \]

一方、命題 8.2.8 より \(N\left( A\right) \subseteq Y\) なので、任意の \(A\)-辺は \(N\left( A\right) \) に属する頂点を唯一つ含む。よって次の不等式が成り立つ:

\[ \begin{aligned} \left(\text{\# } A \text{-辺} \right) & =\sum_{y\in N\left( A\right) }\underbrace{\left(\text{\# } \text{頂点 } y \text{ を含む } A \text{-辺}\right) }_{\substack{\leq\,\deg y}}\\ & \leq\sum_{y\in N\left( A\right) }\underbrace{\deg y}_{\substack{=\,k\\(\because\ G \text{ は } k \text{-正則})}} \\ & = \sum_{y\in N\left( A\right) }k \\ & = k\cdot\left\vert N\left( A\right) \right\vert \end{aligned} \]

よって次を得る:

\[ k\cdot\left\vert N\left( A\right) \right\vert \geq\left(\text{\# } A \text{-辺}\right) =k\cdot\left\vert A\right\vert \]

\(k > 0\) より両辺を \(k\) で割ることができて、\(\left\vert N\left( A\right) \right\vert \geq\left\vert A\right\vert \) が分かる。

\(A\) を固定したことを忘れる。以上で \(X\) の任意の部分集合 \(A\) に対して \(\left\vert N\left( A\right) \right\vert \geq\left\vert A\right\vert \) だと証明できた。よって Hall の結婚定理 (定理 8.3.4) より \(G\) は \(X\)-完全なマッチング \(M\) を持つ。

一方、命題 8.6.6 からは \(\left\vert X\right\vert =\left\vert Y\right\vert \) が分かる。よって命題 8.3.1 (f) よりマッチング \(M\) は完全だと分かる。つまり \(G\) は完全マッチングを持つ。以上で命題 8.6.7 は証明された。□