9.5. Hall–König のマッチング定理の証明
続いて、最大フロー最小カット定理 (定理 9.4.3) を使って Hall–König のマッチング定理 (定理 8.4.7) を証明する。
例 9.2.1 で説明したように、二部グラフ \(\left( G,X,Y\right) \) からネットワーク \(N\) を構築し、\(G\) のマッチングと \(N\) のフローが一対一に対応するようにできる。最大フロー最小カット定理 (定理 9.4.3) より次の等式が分かる:
ここで \(V\) はネットワーク \(N\) を構成する有向グラフの頂点集合を表す。この等式から、\(N\) 上のネットワーク \(f\) と \(N\) のカット \(\left[ S,\overline{S}\right] \) であって \(\left\vert f\right\vert =c\left( S,\overline{S}\right) \) を満たすものが存在すると分かる。この \(f\) と \(S\) に注目する。\(S\) は \(V\) の部分集合であり、\(s \in S\) と \(t \notin S\) を満たす。
フロー \(f\) に対応する \(G\) のマッチングを \(M\) とする (つまり、\(f ( \overrightarrow{e} ) =1\) を満たす \(G\) の辺 \(e\) 全体の集合を \(M\) とする)。このとき \(\left\vert M\right\vert =\left\vert f\right\vert \) が成り立つ。
\(U\colonequals X\cap S\) と定める。\(U\) は \(X\) の部分集合である。簡単な例におけるカット \(\left[ S,\overline{S}\right] \) を表す図を次に示す:
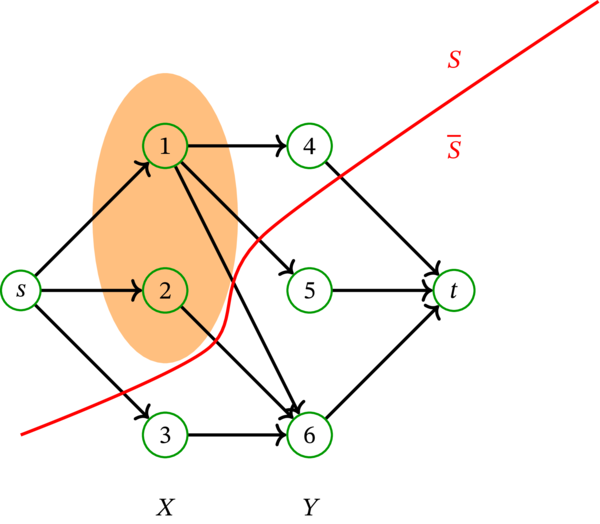
オレンジ色の楕円が集合 \(U\) を表す。
このとき次の等式が分かる:
以上で定理 8.4.7 は証明された。□
Hall–König のマッチング定理 (定理 8.4.7) が証明できたので、Hall の結婚定理 (定理 8.3.4) と König の定理 (定理 8.4.6) も証明された。これらの二つの定理は Hall–König のマッチング定理から導出できると以前に示したからである。
-
[17s-lec16, Lemma 1.42] は多重グラフ \(G\) ではなく単純グラフ \(G\) に対する命題であることに注意してほしい。しかし、これは本質的な違いではない: \(\left( G,X,Y\right) \) が二部グラフで \(G\) が多重グラフなら \(\left( G^{\operatorname*{simp}},X,Y\right) \) も二部グラフであり、\(G^{\operatorname*{simp}}\) のマッチングからは同じ大きさの \(G\) のマッチングが容易に得られる (そして集合 \(N\left( U\right) \) は \(G\) と \(G^{\operatorname*{simp}}\) のどちらを考えたとしても変わらない)。そのため、定理 8.4.7 の証明では一般性を失うことなく \(G\) は単純グラフだと仮定できる。 ↩︎