5.11. BEST 定理: 証明

これで BEST 定理 (定理 5.9.1) を証明する準備が整った。ただ先述したように、最初は BEST' 定理 (定理 5.10.4) を示す。

[証明のアイデア] 弧 \(a\) で始まる \(D\) のオイラー回路を \(a\)-オイラー回路と呼ぶことにする。

\(\mathbf{e}\) を \(a\)-オイラー回路とする。\(\mathbf{e}\) の最初の弧は \(a\) であり、\(\mathbf{e}\) は \(r\) で始まって \(r\) で終わる。オイラー回路である \(\mathbf{e}\) は \(D\) の全ての弧を含む。さらに \(D\) の全ての頂点は \(1\) 以上の出次数を持つので、\(\mathbf{e}\) は \(D\) の全ての頂点を含む。任意の頂点 \(u \neq r\) に対して、\(\mathbf{e}\) が最後に \(u\) を出ていくときの弧を \(e\left( u\right) \) と定義する。つまり、終点が \(u\) の弧の中で \(\mathbf{e}\) における登場位置が最も後ろのものを \(e\left( u\right) \) とする。全ての頂点 \(u \neq r\) に対する \(e\left( u\right) \) を集めた集合を \(\operatorname*{Exit}\mathbf{e}\) と定める。この上で次の命題を示す:

Claim 1: 全域部分有向グラフ \(\left( V,\ \operatorname*{Exit}\mathbf{e},\ \psi|_{\operatorname*{Exit}\mathbf{e}}\right) \) は \(r\) を終根とする \(D\) の全域有向木である (先述した記号の濫用を許すなら、この全域部分有向グラフは「集合 \(\operatorname*{Exit}\mathbf{e}\)」と書ける)。

しばらく Claim 1 が証明できたと仮定して議論を進める。このとき任意の \(a\)-オイラー回路が一つ与えられると \(r\) を終根とする \(D\) の全域有向木が一つ構築できることが分かる。

特定の全域有向木を生成する \(a\)-オイラー回路 \(\mathbf{e}\) はいくつあるだろうか？この質問には都合の良い答えがある:

Claim 2: \(r\) を終根とする \(D\) の全域有向木 \(\left( V,B,\psi\mid _{B}\right) \) のそれぞれに対して、\(\operatorname*{Exit}\mathbf{e}=B\) を満たす \(a\)-オイラー回路 \(\mathbf{e}\) はちょうど \(\prod\limits_{u\in V}\left( \deg^{+}u-1\right) !\) 個だけ存在する。

Claim 2 も証明できたと仮定しよう。Claim 1 と Claim 2 を組み合わせれば、\(a\)-オイラー回路と \(r\) を終根とする \(D\) の全域有向木の間に \(\prod\limits_{u\in V}\left( \deg^{+}u-1\right) !\) 対 \(1\) の対応があることが分かる。よって \(a\)-オイラー回路の個数は \(r\) を終根とする \(D\) の全域有向木の個数の \(\prod\limits_{u\in V}\left( \deg ^{+}u-1\right) !\) 倍だと分かる。これは定理 5.10.4 の主張そのものである。よって後は Claim 1 と Claim 2 を示せれば定理 5.10.4 の証明が完了する。

完全な証明を示す:

[定理 5.10.4 の証明] 最初に用語をいくつか定義する:

頂点 \(u\) の外向き弧 (outgoing arc) とは、始点が \(u\) である弧を意味する。頂点 \(u\) の内向き弧 (incoming arc) とは、終点が \(u\) である弧を意味する。
\(a\)-オイラー回路 (\(a\)-Eulerian circuit) とは、最初の弧が \(a\) である \(D\) のオイラー回路を意味する。
「\(r\) を終根とする \(D\) の全域有向木 (spanning arborescence of \(D\) rooted to \(r\))」を省略して「sparb」と書く。

\(D\) の全域部分有向グラフは必ず \(A\) の部分集合 \(B\) を使って \(\left( V,B,\psi\mid _{B}\right) \) と書ける。つまり、\(D\) の全域部分有向グラフは弧集合 \(B\) によって一意に決定する。

そこで以降の議論では、弧集合 \(B\) が特定する \(D\) の全域部分有向グラフ \(\left( V,B,\psi|_{B}\right) \) を \(B\) と表記する。逆方向にも同様に、\(D\) の全域部分有向グラフ \(\left( V,B,\psi|_{B}\right) \) が特定する \(A\) の部分集合 \(B\) を \(\left( V,B,\psi|_{B}\right) \) と表記する。このため、例えば「\(A\) の部分集合 \(B\) は sparb である」などと言う。この一文は「\(B\) に対応する全域部分有向グラフ \(\left( V,B,\psi|_{B}\right) \) が sparb である」を意味する。

任意の \(a\)-オイラー回路 \(\mathbf{e}\) に対して、\(A\) の部分集合 \(\operatorname*{Exit}\mathbf{e}\) を次のように定める:

\(\mathbf{e}\) を \(a\)-オイラー回路とする。\(\mathbf{e}\) の最初の弧は \(a\) であり、\(\mathbf{a}\) は \(r\) で始まって \(r\) で終わる。オイラー回路である \(\mathbf{e}\) は \(D\) の全ての弧を含む。さらに \(D\) の全ての頂点は \(1\) 以上の出次数を持つので、\(\mathbf{e}\) は \(D\) の全ての頂点を含む。任意の頂点 \(u\in V\setminus \left\{ r\right\} \) に対して、\(\mathbf{e}\) が最後に \(u\) を出ていくときの弧を \(e\left( u\right) \) と定義する。つまり、終点が \(u\) の弧の中で \(\mathbf{e}\) における登場位置が最も後ろのものを \(e\left( u\right) \) とする。そして、全ての頂点 \(u\in V\setminus\left\{ r\right\} \) に対する \(e\left( u\right) \) を集めた集合を \(\operatorname*{Exit}\mathbf{e}\) と定義する。つまり、それぞれの \(a\)-オイラー回路 \(\mathbf{e}\) に対して \(A\) の部分集合 \(\operatorname*{Exit}\mathbf{e}\) が定義される。

例 5.11.1

\(\operatorname*{Exit}\mathbf{e}\) の例を示す。\(D\) を次の多重有向グラフとする:

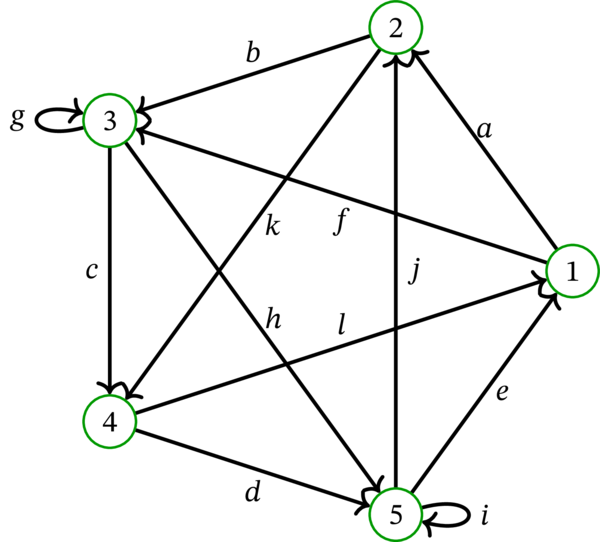
\(r = 1\) として、\(\mathbf{e}\) を次の \(a\)-オイラー回路と定める:

\[ \left( 1,a,2,b,3,c,4,d,5,e,1,f,3,g,3,h,5,i,5,j,2,k,4,l,1\right) \]

[オイラー回路で弧がアルファベット順になるように弧の名前を付けてある。] このとき次の等式が成り立つ:

\[ e\left( 2\right) =k,\quad e\left( 3\right)=h, \quad e\left( 4\right) =l, \quad e\left(5\right) =j \]

ここから \(\operatorname*{Exit}\mathbf{e}=\left\{ k,h,l,j\right\} \) が分かる。\(\operatorname*{Exit}\mathbf{e}\) が定める全域部分有向グラフを次に示す:

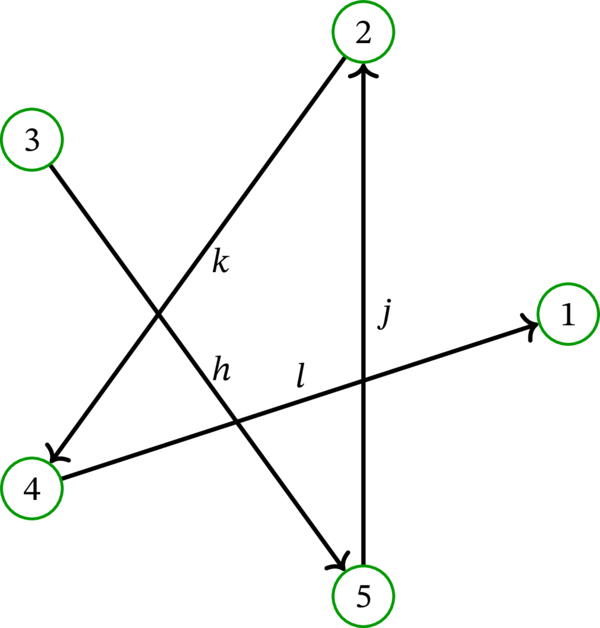
続いて次の命題を示す:

Claim 1: \(\mathbf{e}\) を \(a\)-オイラー回路とする。このとき \(\operatorname*{Exit}\mathbf{e}\) は sparb である。

Claim 2: 任意の sparb \(B\) (\(A\) の部分集合として表されている) に対して、\(\operatorname*{Exit}\mathbf{e}=B\) を満たす \(a\)-オイラー回路 \(\mathbf{e}\) はちょうど \(\prod\limits_{u\in V}\left( \deg^{+}u-1\right) !\) 個だけ存在する。

[Claim 1 の証明: 集合 \(\operatorname*{Exit}\mathbf{e}\) は各頂点 \(u\in V\setminus\left\{ r\right\} \) の外向き弧をちょうど一つずつ含み、\(r\) の外向き弧は含まない。よって \(\left\vert \operatorname*{Exit}\mathbf{e}\right\vert =\left\vert V\right\vert -1\) が成り立つ。

\(\mathbf{e}\) の弧を順番に \(a_{1},a_{2},\ldots,a_{m}\) とする (例えば、\(\mathbf{e}\) の最初の弧は \(a\) なので \(a_{1}=a\) となる)。

\(\operatorname*{Exit}\mathbf{e}\) に属する弧は何らかの \(u\in V\setminus\left\{ r\right\} \) に対する \(e\left( u\right) \) だった (上述の定義より ── 弧 \(e\left( u\right) \) は \(\mathbf{e}\) が最後に \(u\) を出ていくときの弧を表す)。そういった弧をこれから最終出口弧 (last-exit arc) と呼ぶ。

各 \(u\in V\setminus\left\{ r\right\} \) に対して、\(e\left( u\right) =a_{i}\) が成り立つ一意な自然数 \(i\in\left\{ 1,2,\ldots,m\right\} \) を \(j\left( u\right) \) とする。 [この自然数 \(i\) が一意に定まることは、\(D\) の全ての弧が \(\mathbf{e}\) にちょうど一度ずつ現れることから分かる。] つまり、\(j\left( u\right) \) はオイラー回路 \(\mathbf{e}\) における弧 \(e\left( u\right) \) の最後の登場位置を表す。\(e\left( u\right) \) は \(\mathbf{e}\) が最後に \(u\) を出ていくときの弧なので、オイラー回路 \(\mathbf{e}\) は \(e\left( u\right) \) より後に頂点 \(u\) を訪れない。

よって、最終出口弧 \(e\left( u\right) \) が終点 \(v \neq r\) を持つなら、次の不等式が成り立つ:

\[ j\left( u\right) < j\left( v\right) \qquad (1) \]

[弧 \(e\left( u\right) \) によって回路 \(\mathbf{e}\) は頂点 \(v\) に移動し、その後 \(\mathbf{e}\) は少なくとも一度 \(v\) を離れる。よって対応する最終出口弧 \(e\left( v\right) \) は \(\mathbf{e}\) で \(e\left( u\right) \) より後ろにある。]

\(r\) が \(\operatorname*{Exit}\mathbf{e}\) の終根 (正確に言えば、全域部分有向グラフ \(\left( V,\operatorname*{Exit}\mathbf{e},\psi|_{\operatorname*{Exit}\mathbf{e}}\right) \) の終根) だと示す。これを示すには、各頂点 \(v \in V\) に対して \(v\) から \(r\) への路が有向グラフ \(\left( V,\operatorname*{Exit}\mathbf{e},\psi |_{\operatorname*{Exit}\mathbf{e}}\right) \) に存在することを示せばよい。

頂点 \(v \in V\) を任意に取る。有向グラフ \(\left( V,\operatorname*{Exit}\mathbf{e},\psi\mid _{\operatorname*{Exit}\mathbf{e}}\right) \) が持つ \(v\) から \(r\) への路を見つけなければならない。命題 4.5.8 より、\(v\) から \(r\) への歩道を見つければ十分である。言い換えれば、\(D\) の最終出口弧だけからなる \(v\) から \(r\) への歩道を見つける必要がある。

歩道の始点を \(v\) とする。もし \(v=r\) なら、条件を満たす歩道は明らかに存在する。そうでなければ \(v\in V\setminus\left\{ r\right\} \) なので、最終出口弧 \(e\left( v\right) \) と \(j\left( v\right) \) が定義される。\(v\) から弧 \(e\left( v\right) \) を進んだ先の頂点を \(v^{\prime}\) とする。\(v^{\prime}\) は弧 \(e\left( v\right) \) の終点なので、式 \((1)\) より \(j\left( v\right) < j\left( v^{\prime}\right) \) を満たす。もし \(v^{\prime} = r\) なら条件を満たす歩道が完成する。そうでなければ、\(e\left( v^{\prime}\right) \) と \(j\left( v^{\prime}\right) \) が定義されるので、さらに \(e\left( v^{\prime }\right) \) を進む。\(e\left( v^{\prime }\right) \) を進んだ先の頂点を \(v^{\prime\prime}\) とする。ここでも\(v^{\prime\prime}\) は弧 \(e\left( v^{\prime}\right) \) の終点なので、式 \((1)\) より \(j\left( v^{\prime}\right) < j\left( v^{\prime\prime}\right) \) を満たす。もし \(v^{\prime\prime} = r \) なら条件を満たす歩道が完成する。そうでなければ、この議論を繰り返すことで次の歩道を構築できる:

\[ \left( v,e\left( v\right) ,v^{\prime},e\left( v^{\prime}\right) ,v^{\prime\prime},e\left( v^{\prime\prime}\right) ,\ldots\right) \]

この歩道は無限に続くか、そうでなければ頂点 \(r\) で終了する。

しかし、不等式 \(j\left( v\right) < j\left( v^{\prime}\right) < j\left( v^{\prime\prime}\right) < \cdots\) が成り立つので、\(j\left( v\right) ,j\left( v^{\prime}\right) ,j\left( v^{\prime\prime}\right) ,\ldots\) は全て異なる。そして \(j\) の値域 \(\left\{ 1,2,\ldots,m\right\} \) は有限集合である。そのため、この歩道が無限に続くことはない。よって、この歩道は頂点 \(r\) で終了する。最終出口弧だけを使った \(v\) から \(r\) への歩道が見つかったので、\(\operatorname*{Exit}\mathbf{e}\) は \(v\) から \(r\) への歩道を持つ。つまり \(\operatorname*{Exit}\mathbf{e}\) は \(v\) から \(r\) への路を持つ。

\(v\) を固定したことを忘れる。各頂点 \(v \in V\) に対して有向グラフ \(\left( V,\operatorname*{Exit}\mathbf{e},\psi|_{\operatorname*{Exit}\mathbf{e}}\right) \) が \(v\) から \(r\) への路を持つことが以上の議論で示せた。言い換えれば、\(r\) は \(\operatorname*{Exit}\mathbf{e}\) の終根である。よって有向木の同値性定理の双対 (定理 5.10.5) における A'2 \(\Longrightarrow\) A'1 と \(\left\vert \operatorname*{Exit}\mathbf{e}\right\vert =\left\vert V\right\vert -1\) から、\(\operatorname*{Exit}\mathbf{e}\) が \(r\) を終根とする有向木だと分かる。つまり \(\operatorname*{Exit}\mathbf{e}\) は sparb である。これで Claim 1 は証明された。]

[Claim 2 の証明: \(B\) を任意の sparb とする。 [先述したように \(B\) は弧の集合であり、\(B\) で特定される全域部分有向グラフ \(\left( V,B,\psi |_{B}\right) \) を \(B\) と表している。]

\(\operatorname*{Exit}\mathbf{e}=B\) を満たす \(a\)-オイラー回路 \(\mathbf{e}\) がちょうど \(\prod\limits_{u\in V}\left( \deg ^{+}u-1\right) !\) 個だけ存在すると示す必要がある。

\(B\) に属する弧を \(B\)-弧 (\(B\)-arc) と呼ぶことにする。\(B\) は sparb なので、\(r\) を終根とする有向木である。よって有向木の同値性定理の双対 (定理 5.10.5) における A'1 \(\Longrightarrow\) A'6 から、\(B\) の頂点の出次数について次の等式が分かる:

\[ \begin{cases} \deg_{B}^{+}r = 0 \\ \deg_{B}^{+}v =1 \ \ \left(\forall v\in V\setminus\left\{ r\right\}\right) \end{cases} \]

ここで \(\deg_{B}^{+}v\) は有向グラフ \(\left( V,B,\psi|_{B}\right) \) における頂点 \(v\) の出次数を表す。一つ目の等式を言い換えれば、\(r\) を始点とする \(B\)-弧は存在しない。一方で二つ目の等式からは、任意の頂点 \(u\in V\setminus\left\{ r\right\} \) に対して始点 \(u\) を持つ \(B\)-弧がちょうど一つ存在することが分かる。

続いて、\(\operatorname*{Exit}\mathbf{e}=B\) を満たす \(a\)-オイラー回路 \(\mathbf{e}\) の個数を数える。

\(a\)-オイラー回路 \(\mathbf{e}\) を次のように構築することを考える:

有向グラフ \(D\) の頂点を弧に沿って移動できる亀がいて、その亀が \(D\) の弧を全て一度ずつ使って移動したいと考えているとする。この亀は頂点 \(r\) から移動を始め、最初は弧 \(a\) に沿って移動する。その後、亀は有向グラフの歩道と同じように移動する: 頂点に到着すると、その頂点から出る弧を適当に選び、その弧の終点に移動する。そのとき亀は次の二つの規則に従うとする:

以前に使った弧は使わない。
必要でない限り \(B\)-弧を使わない。つまり、現在の頂点の外向き弧で未使用のものが \(B\)-弧だけになったときに限って \(B\)-弧を使う。

\(D\) は有限個の弧しか持たないので、この亀は必ずどこかの頂点で停止する (移動に使える弧が存在しない状態になる)。

この亀が停止するまでの軌跡が表す歩道を \(\mathbf{w}\) とする。\(\mathbf{w}\) は小道 (同じ弧を二度通らない歩道) であり、頂点 \(r\) と弧 \(a\) から始まる。

以降では \(\mathbf{w}\) が \(\operatorname*{Exit}\mathbf{w}=B\) を満たす \(a\)-オイラー回路であることを見る。まずは例を一つ示す:

例 5.11.2

\(D\) を次の多重有向グラフとする:

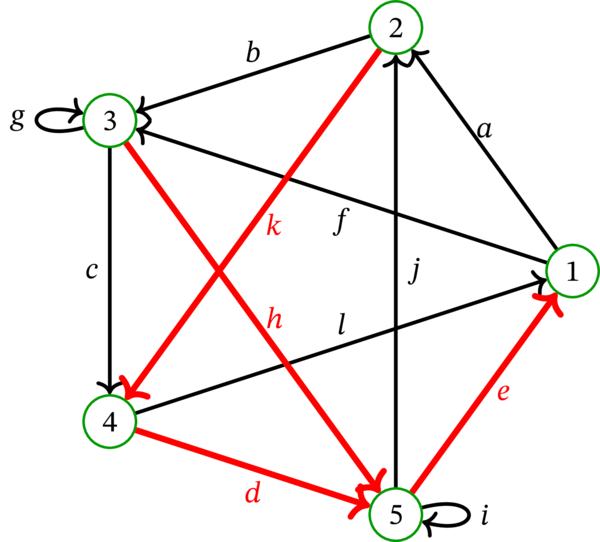
[弧の名前は説明が簡単になるように付けてある。] \(r = 1\) および \(a = a\) とする。\(B\) が集合 \(\left\{ d,e,h,k\right\} \) のとき、\(B\) が特定する \(D\) の全域部分有向グラフ (赤い弧が表すグラフ) は全域有向木である。

亀は最初 \(r=1\) を出発し、\(a\) に沿って頂点 \(2\) に移動する。頂点 \(2\) の外向き弧は \(b\) と \(k\) であるものの、\(k\) は \(B\)-弧なので選ぶことはできない。よって亀は \(b\) に沿って頂点 \(3\) に移動する。頂点 \(3\) の外向き弧は \(c\), \(g\), \(h\) であり、この中で \(h\) は \(B\)-弧なので選択できない。ここでは亀が弧 \(g\) を選ぶとする。\(g\) はループなので、亀は頂点 \(3\) に到着する。亀が次に選べる弧は \(c\) しかない (\(g\) は使用済みであり、\(h\) は \(B\)-弧であるため)。\(c\) に沿って頂点 \(4\) に移動した亀は、続いて (唯一の選択肢として) 弧 \(l\) を選択する。\(l\) に沿って頂点 \(1\) に移動し、続いて \(f\) に沿って頂点 \(3\) に移動する。ここで亀は初めて \(B\)-弧 \(h\) を選択する (\(h\) 以外の外向き弧が全て消費済みであるため)。\(h\) に沿って移動した後の頂点 \(5\) では \(e\) が \(B\)-弧なので、弧 \(j\) と弧 \(i\) が選択肢となる。ここでは亀が弧 \(j\) を選ぶとする。頂点 \(2\) に移動した亀は次に \(B\)-弧 \(k\) に沿って頂点 \(4\) に移動する。その後は \(B\)-弧 \(d\), ループ \(i\), \(B\)-弧 \(e\) を順に移動して頂点 \(1\) に移動し、そこで移動できる弧がなくなる。このとき次の歩道が \(\mathbf{w}\) となる:

\[ \mathbf{w}=\left( 1,a,2,b,3,g,3,c,4,l,1,f,3,h,5,j,2,k,4,d,5,i,5,e,1\right) \]

[もちろん、これ以外の歩道が得られる可能性もある。]

一般的な定理の証明に戻る。亀の軌跡を表す歩道 \(\mathbf{w}\) の特徴を調べよう。

まず、\(\mathbf{w}\) が閉歩道である (\(r\) で終わる) ことが分かる。

証明: 背理法で示す。\(\mathbf{w}\) の終点を \(u\) として、\(u \neq r\) と仮定する。つまり亀が \(r\) でない頂点で移動を停止したとする。このとき \(\mathbf{w}\) が頂点 \(u\) に入る回数は \(\mathbf{w}\) が頂点 \(u\) から出ていく回数より多い (\(\mathbf{w}\) の終点が \(u\) で始点は \(u\) でないため)。言い換えれば、亀が頂点 \(u\) に移動する回数は頂点 \(u\) を離れる回数より多い。亀が頂点 \(u\) に移動できるのは最大でも \(\deg^{-}u\) 回 (同じ弧は二度使えず、終点が \(u\) の弧は \(\deg^{-}u\) 個あるため) だから、亀が頂点 \(u\) を離れる回数は \(\deg^{-}u\) 未満である。一方 \(D\) は平衡なので \(\deg^{-}u=\deg^{+}u\) が成り立つ。よって亀が頂点 \(u\) を離れる回数は \(\deg^{+}u\) 未満だと分かる。つまり、亀が頂点 \(u\) で移動を停止したとき、\(u\) の外向き弧であって亀が使っていないものが存在する。これは亀が移動を停止できないことを意味する。これは矛盾なので、仮定が偽だと分かる。以上で \(\mathbf{w}\) が閉歩道だと証明できた。□

言い換えれば、\(\mathbf{w}\) は回路である。続いて \(\mathbf{w}\) がオイラー回路だと示す。

そのために、用語をさらに定義する: \(u\) を \(D\) の頂点とする。\(u\) の外向き弧が全て亀によって使われているとき (\(u\) の外向き弧が全て \(\mathbf{w}\) に含まれるとき)、\(u\) を消費済み (exhausted) と呼ぶ。

\(\mathbf{w}\) は回路なので、\(\mathbf{w}\) の始点と終点はどちらも頂点 \(r\) である。よって亀は \(r\) で移動を停止している。つまり頂点 \(r\) は消費済みである。

これから \(D\) の全ての頂点が消費済みだと示す。

証明: 背理法で示す。\(D\) の頂点 \(u\) が消費済みでないと仮定して、この \(u\) に注目する。\(B\) は sparb だから、\(B\) は \(r\) を終根とする有向木であり、\(r\) は \(B\) の終根である。よって \(u\) から \(r\) への路 \(\mathbf{p}=\left( p_{0},b_{1},p_{1},b_{2},p_{2},\ldots ,b_{k},p_{k}\right) \) が \(B\) に存在する。この路に注目すると、\(p_{0}=u\) および \(p_{k}=r\) であり、全ての弧 \(b_{1},b_{2},\ldots,b_{k}\) が \(B\) に属することが分かる。

頂点 \(p_{i}\) が消費済みであるような \(i\in\left\{ 0,1,\ldots,k\right\} \) は少なくとも一つ存在する (例えば \(i=k\) とすれば \(p_{k}=r\) は消費済みである)。この条件を満たす最小の \(i\) を考える。\(p_{0}=u\) は消費済みでないので、\(p_{i}\neq p_{0}\) が分かる。つまり \(i \geq 1\) であり、\(p_{i-1}\) が存在する。このとき \(i\) の定義から \(p_{i-1}\) は消費済みでない。

弧 \(b_{i}\) は始点 \(p_{i-1}\) と終点 \(p_{i}\) を持つ。そのため弧 \(b_{i}\) は頂点 \(p_{i-1}\) の外向き弧であり、頂点 \(p_{i}\) の内向き弧でもある。さらに、\(b_{i}\) は \(B\) に属する (\(\mathbf{p}\) の全ての弧 \(b_{1},b_{2},\ldots,b_{k}\) が \(B\) に属するため)。

有向グラフ \(D\) は平衡なので、\(\deg^{+} p_{i} =\deg ^{-} p_{i} \) が分かる。

頂点 \(p_{i}\) は消費済みである。定義を使って言い換えれば、亀は \(p_{i}\) の外向き弧を全て使っている。亀は同じ弧を二度使わないので、これは亀が \(p_{i}\) が持つちょうど \(\deg^{+} p_{i} \) 個の外向き弧を全て使ったことを意味する (\(\deg^{+} p_{i} \) は \(D\) における \(p_{i}\) の外向き弧の個数を表すため)。\(\deg^{+} p_{i} =\deg^{-} p_{i} \) を使って言い換えれば、亀は \(p_{i}\) の外向き弧をちょうど \(\deg^{-} p_{i} \) 個だけ使ったと分かる。

一方、亀の軌跡は閉歩道なので、亀が \(p_{i}\) に移動する回数と \(p_{i}\) から離れる回数は等しい。言い換えれば、亀が使った \(p_i\) の内向き弧の個数と \(p_i\) の外向き弧の個数は等しい。前段落の議論より後者の値は \(\deg^{-} p_{i} \) なので、前者の値も \(\deg^{-} p_{i} \) だと分かる。\(\deg^{-} p_{i} \) は \(D\) における \(p_{i}\) の内向き弧の総数なので (そして亀は同じ弧を二度使わないので)、亀は \(p_{i}\) の内向き弧を全て使ったと結論できる。

よって特に、亀は \(b_{i}\) を使っている。\(b_{i}\) は \(B\)-弧なので、亀は \(b_{i}\) を最後に (\(b_{i}\) ではない \(p_{i-1}\) の外向き弧を使った後に) 使う。よって \(b_{i}\) を使った亀は \(p_{i-1}\) の外向き弧を全て使っていると分かる。言い換えれば、\(p_{i-1}\) は消費済みである。しかし、これは \(p_{i-1}\) が消費済みである事実と矛盾する！この矛盾から仮定が偽だと分かる。これで証明は完了した¹。

\(D\) の全ての頂点が消費済みだと分かった。言い換えれば、亀は \(D\) の弧を全て使っている。つまり小道 \(\mathbf{w}\) は \(D\) の全ての弧を含む。\(\mathbf{w}\) は小道かつ閉歩道だから、\(\mathbf{w}\) は \(D\) のオイラー回路だと結論できる。さらに、\(\mathbf{w}\) は頂点 \(r\) と弧 \(a\) から始まるから、\(\mathbf{w}\) は \(a\)-オイラー回路である。亀は \(B\)-弧を最後に使う (そして \(\mathbf{w}\) がオイラー回路なので亀は \(B\)-弧を全て使っている) ので、\(\operatorname*{Exit}\mathbf{w}=B\) が分かる。

よって、今考えている亀の軌跡は \(\operatorname*{Exit}\mathbf{e}=B\) を満たす \(a\)-オイラー回路 \(\mathbf{w}\) を生成する。一方、亀が移動する中で選択肢が複数ある状況が存在する。具体的に言えば、頂点 \(u\in V\) に移動した亀は次の弧をある程度自由に選択できる。選択できる弧は始点が \(u\) の未使用の弧であり、加えて次の条件を満たす必要がある:

\(u \neq r\) なら、唯一の² \(B\)-弧は最後に使う。
\(u=r\) なら、弧 \(a\) を最初に使う。

亀が生成できる軌跡の個数を数えよう。議論を明確にするために、上述の手続きを少し変更する: 弧の選択を移動しながら行うのではなく、移動を始める前に弧を全て選択する。具体的には、各頂点 \(u \in V\) に対して、\(u\) を始点に持つ弧全体の集合上に次の条件を満たす全順序を事前に定義する:

\(u \neq r\) なら、唯一の \(B\)-弧を順序の末尾にする。
\(u=r\) なら、\(a\) を順序の先頭にする。

始点が \(u\) の弧は \(\deg^{+}u\) 存在し、その中で順序が固定される一つを除けば弧の順序は自由に選択できる。よって、この条件を満たす全順序は \(\left( \deg^{+}u-1\right) !\) 個存在する。全順序が決まると、亀は移動を開始する: 頂点 \(u\) に初めて到着したとき、亀はこの全順序で先頭にある弧に沿って \(u\) を離れる。そして、頂点 \(u\) に二度目に到着した亀は、この全順序で二番目にある弧を使って \(u\) を離れる。以降も同様となる。

つまり亀の軌跡には \(\prod\limits_{u\in V}\left( \deg^{+}u-1\right) !\) 個の選択肢があり、この選択肢のそれぞれが異なる \(a\)-オイラー回路 \(\mathbf{e}\) を生成する (各頂点に対応する全順序が異なると生成される \(\mathbf{e}\) も異なるため: 各頂点に対応する全順序は、その頂点を始点に持つ弧が \(\mathbf{e}\) で使われる順番を表す)。さらに、\(\operatorname*{Exit}\mathbf{e}=B\) を満たす任意の \(a\)-オイラー回路 \(e\) に対して、\(\mathbf{e}\) を生成する亀の軌跡が存在する³。

以上の議論より、\(\operatorname*{Exit}\mathbf{e}=B\) を満たす \(a\)-オイラー回路 \(\mathbf{e}\) の個数は、亀の軌跡の選択肢の個数 \(\prod\limits_{u\in V}\left( \deg^{+}u-1\right) !\) に等しい。これで Claim 2 は証明された。]

Claim 1 と Claim 2 が証明されたので、もう一息で証明が完了する。Claim 1 より、次の写像は well-defined だと分かる:

\[ \begin{aligned} \left\{ D \text{ の } a\text{-オイラー回路}\right\} & \rightarrow\left\{ \text{sparb}\right\} \\ \mathbf{e} & \mapsto\operatorname*{Exit}\mathbf{e} \end{aligned} \]

さらに Claim 2 からは、この写像が \(\prod\limits_{u\in V}\left( \deg^{+}u-1\right) !\) 対 \(1\) の対応だと分かる⁴ (言い換えれば、この写像の下で任意の sparb はちょうど \(\prod\limits_{u\in V}\left( \deg ^{+}u-1\right) !\) 個の原像を持つ)。よって multijection principle⁵ より、次の等式が分かる⁶:

\[ \left(\text{\# } D \text{ の } a \text{-オイラー回路}\right) = \left( \prod\limits_{u\in V}\left( \deg^{+}u-1\right) !\right) \cdot\left(\text{\# } \text{sparb}\right) \]

定理の設定より \(\varepsilon\left( D,a\right) =\left(\text{\# } D \text{ の } a \text{-オイラー回路}\right) \) および \(\tau\left( D,r\right) =\left(\text{\# } \text{sparb}\right) \) だから、次の等式を得る:

\[ \begin{aligned} \varepsilon\left( D,a\right) & =\left( \prod\limits_{u\in V}\left( \deg ^{+}u-1\right) !\right) \cdot\tau\left( D,r\right) \\ & =\tau\left( D,r\right) \cdot\prod\limits_{u\in V}\left( \deg^{+}u-1\right) ! \end{aligned} \]

これで定理 5.10.4 は証明された。□

[定理 5.9.1 の証明] 以前に説明した通り、定理 5.10.4 で弧を反転させれば (有向グラフ \(D^{\operatorname*{rev}}\) に定理 5.10.4 を適用すれば) 定理 5.9.1 が得られる。□

異なる視点を提供するために、命題「\(D\) の全ての頂点は消費済みである」の別証明を示す。

背理法で示す。消費済みでない \(D\) の頂点 \(u\) が存在すると仮定し、この \(u\) に注目する。\(u\) が消費済みでないので、少なくとも一つの \(u\) の外向き弧を亀は使っていない。よって \(u\) を始点とする \(B\)-弧は亀によって使われていない (亀は \(B\)-弧を最後に使うため)。その \(B\)-弧を \(f\) として、\(f\) の終点を \(u^{\prime}\) とする。亀は \(f\) を使っていないので、未使用の \(u^{\prime}\) の内向き弧が存在する。よって未使用の \(u^{\prime}\) の外向き弧も存在する (亀が \(u^{\prime}\) に移動する回数と \(u^{\prime}\) を離れる回数は同じであり、\(D\) は平衡より \(\deg^{-} u^{\prime} =\deg^{+} u^{\prime}\) が成り立つため)。言い換えれば、頂点 \(u^{\prime}\) は消費済みでない。

つまり、消費済みでない頂点 \(u\) から \(B\)-弧である外向き弧に沿って移動すると、またしても消費済みでない頂点 \(u^{\prime}\) に到着する。\(u\) を \(u^{\prime}\) に変更して同じ議論を適用すれば、\(u^{\prime}\) から \(B\)-弧に沿って移動することで消費済みでない頂点 \(u^{\prime\prime}\) に到着すると分かる。この議論を続けると、消費済みでない頂点の無限列 \(\left( u,u^{\prime},u^{\prime\prime},\ldots\right) \) が手に入る。\(D\) は有限個の頂点しか持たないので、この無限列には同じ頂点が二つ含まれる。例えば \(u^{\prime\prime}=u^{\prime\prime\prime\prime\prime}\) とする。このとき、無限列の \(u^{\prime\prime}\) から \(u^{\prime\prime\prime\prime\prime}\) の部分を使うと次に示す閉歩道 \(\mathbf{v}\) を構築できる:

\[ \mathbf{v} = \left( u^{\prime\prime},\ast,u^{\prime\prime\prime},\ast,u^{\prime\prime\prime\prime},\ast,u^{\prime\prime\prime\prime\prime}\right)\]

無限列の構成より、\(\mathbf{v}\) の弧は全て \(B\)-弧である (そして当然全て異なる)。\(\mathbf{v}\) の長さは \(1\) 以上なので、\(\mathbf{v}\) は路でない。よって命題 4.5.9 より \(w\) は閉路を含む。つまり、有向グラフ \(\left( V,B,\psi|_{B}\right) \) は閉路を持つ。しかし有向グラフ \(\left( V,B,\psi|_{B}\right) \) は有向木だから閉路を持たない (有向木の定義より \(D^{\operatorname*{und}}\) は閉路を持たず、\(D\) の閉路は \(D^{\operatorname*{und}}\) の閉路にもなるため)。以上で矛盾が導けたので、仮定が偽だと分かる。よって \(D\) の全ての頂点は消費済みである。 ↩︎
B は sparb なので、始点が \(u\) の \(B\)-弧はちょうど一つしか存在しない。 ↩︎
証明: \(\operatorname*{Exit}\mathbf{e}=B\) を満たす任意の \(a\)-オイラー回路を \(\mathbf{e}\) とする。このとき、各頂点に対応する全順序を適切に定めれば、軌跡が \(\mathbf{e}\) となるように亀を移動させることができる。もちろん、各頂点に対応する全順序が「適切」かどうかは \(\mathbf{e}\) に依存する: 任意の頂点 \(u \in V\) に対して、始点が \(u\) の弧全体の集合上の「適切」な全順序とは、\(\mathbf{e}\) でそれらの弧が現れる順序である。こうしたとき全順序が満たすべき条件は満たされる: 弧 \(a\) は \(\mathbf{e}\) の最初の弧なので \(r\) の全順序で最初にあり、各頂点に対応する \(B\)-弧は \(\mathbf{e}\) で (その頂点を始点とする弧の中で) 最後に使われるので \(r\) でない頂点の全順序で最後にある。 ↩︎
\(f\colon X\rightarrow Y\) を写像とする。\(Y\) の各要素が \(f\) に関する原像をちょうど \(m\) 個持つ (\(m \geq 0\)) とき、\(f\) を \(m\) 対 \(1\) の対応 (\(m\)-to-\(1\) correspondence) と呼ぶ。 ↩︎
multijection principle とは、数え上げに関する次の基礎的な事実を言う: \(X\), \(Y\) を有限集合、\(m\) を非負の自然数とする。写像 \(f\colon X\rightarrow Y\) が \(m\) 対 \(1\) の対応 (\(Y\) の各要素がちょうど \(m\) 個の原像を持つ写像) のとき、\(\left\vert X\right\vert =m\cdot\left\vert Y\right\vert \) が成り立つ。

例えば、\(n\) 匹の (五体満足な) 羊は全部で \(4n\) 個の足を持つ。羊の足から羊への写像が \(4\) 対 \(1\) の対応だからである。 ↩︎
「\(\#\)...」は「... の個数」を意味する。 ↩︎