10.2. Gallai-Milgram の定理
続いて、これまでに見てきたものより知名度が低い路の性質を紹介する。
10.2.1定義
最初の性質を表明するには、次の三つの定義が必要になる:
多重有向グラフ \(D\) の二頂点 \(u\), \(v\) が隣接する (adjacent) とは、無向グラフ \(D^{\operatorname*{und}}\) で \(u\) と \(v\) が隣接することを言う。
多重有向グラフ \(D\) の独立集合 (independent set) とは、 \(\operatorname*{V}\left( D\right) \) の部分集合 \(S\) であって任意の二要素が隣接しないものを言う。言い換えれば、無向グラフ \(D^{\operatorname*{und}}\) の独立集合が \(D\) の独立集合である。
多重有向グラフ \(D\) の路被覆 (path cover) とは、\(D\) の路からなる集合であって \(D\) の任意の頂点がちょうど一つの要素に含まれるようなものを言う。
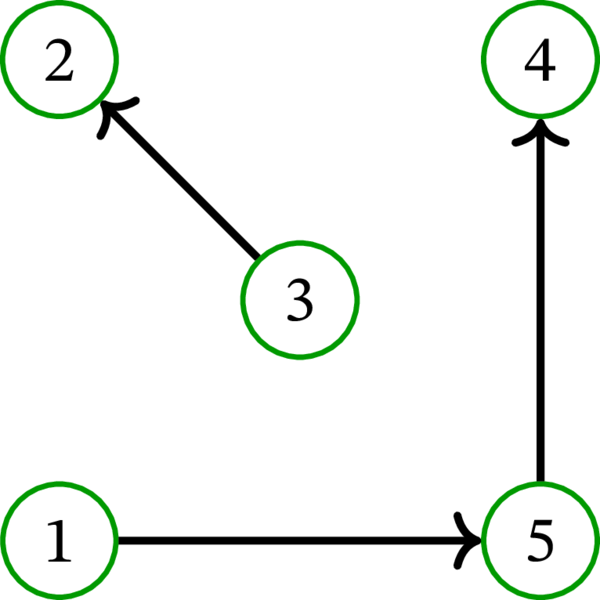
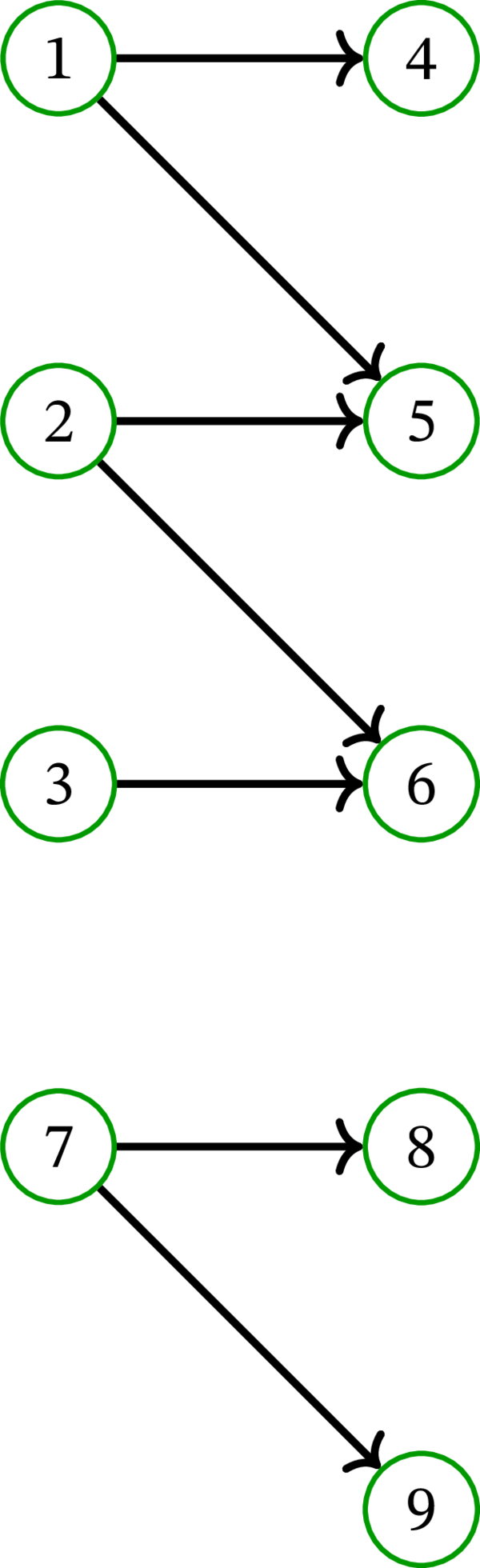
\(D\) を次の多重有向グラフとする:
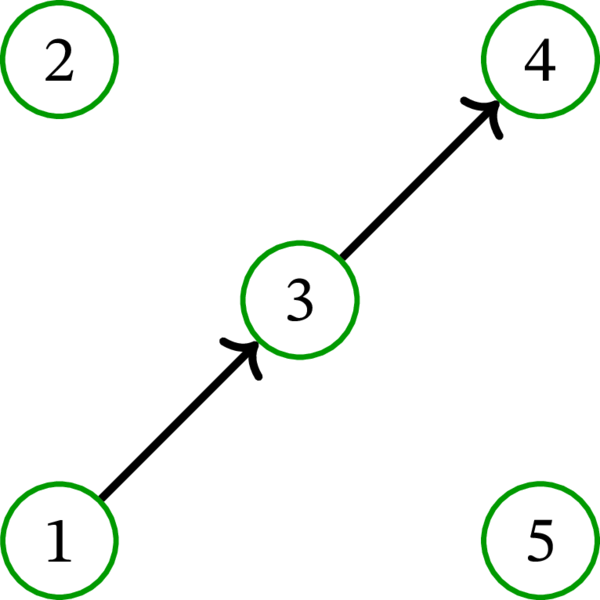
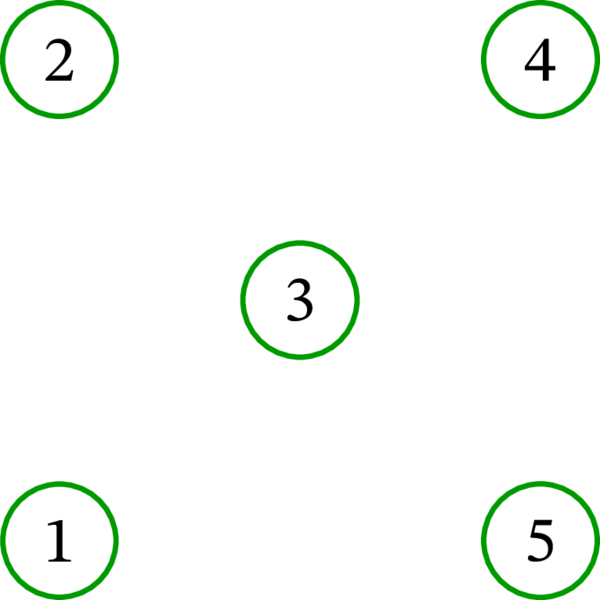
このとき \(\left\{ \left( 1,\ast,5,\ast,4\right) ,\ \left( 3,\ast,2\right) \right\} \) は \(D\) の路被覆である (路に含まれる弧は両端の頂点から一意に定まる上に重要でないので、以前と同様にアスタリスクを使って省略している)。また、\(\left\{ \left( 1,\ast,3,\ast ,4\right) ,\ \left( 2\right) ,\ \left( 5\right) \right\} \) や \(\left\{ \left( 1\right) ,\ \left( 2\right) ,\ \left( 3\right) ,\ \left( 4\right) ,\ \left( 5\right) \right\} \) も \(D\) の路被覆である。これら以外にも \(D\) の路被覆は多くある。
集合 \(\left\{ \left( 1,\ast,5,\ast,4\right) ,\ \left( 3,\ast,2,\ast,4\right) \right\} \) は \(D\) の路被覆でないことに注意してほしい。頂点 \(4\) が二つの要素に含まれるためである (各頂点は路被覆のちょうど一つの要素に含まれる必要がある)。
上述の三つの路被覆を図にすると次のようになる。ここでは路被覆に含まれる弧だけを示し、\(D\) の他の弧は無視している:
\(D\) を有向グラフとする。一つの要素からなる \(D\) の路被覆は、\(D\) のハミルトン路を表す。より正確に言えば、単一の路 \(\mathbf{p}\) だけから構成される \(D\) の路被覆 \(\left\{ \mathbf{p}\right\} \) が存在するのは、\(\mathbf{p}\) がハミルトン路であるとき、かつそのときに限る。
10.2.2Gallai–Milgram の定理
Gallai–Milgram の定理は次の命題である:
\(D\) をループレスな多重有向グラフとする。このとき、\(D\) の路被覆 \(\mathcal{P}\) と \(D\) の独立集合 \(S\) であって、\(\mathcal{P}\) を構成する任意の路に属する \(S\) の頂点がちょうど一つである (言い換えれば、任意の \(\mathbf{p}\in\mathcal{P}\) に対して、\(\mathbf{p}\) の頂点のちょうど一つが \(S\) に属する) ものが存在する。
例 10.2.4 の有向グラフを \(D\) とする。定理 10.2.6 によれば、\(D\) の路被覆 \(\mathcal{P}\) と \(D\) の独立集合 \(S\) であって \(\mathcal{P}\) を構成する任意の路が \(S\) の頂点をちょうど一つ含むものが存在する。条件を満たす路被覆と独立集合として \(\mathcal{P}=\left\{ \left( 1,\ast,5,\ast,4\right) ,\ \left( 3,\ast,2\right) \right\} \) と \(S=\left\{ 5,3\right\} \) がある。
これから Gallai–Milgram の定理を証明する。この証明は Diestel による書籍 [Dieste17, Theorem 2.5.1] を参考にしている:
多重有向グラフ \(D\) を \(D=\left( V,A,\varphi\right) \) と書く。まず用語を一つ定義する:
-
\(\mathcal{P}\) を \(D\) の路被覆とする。\(\mathcal{P}\) の横断カット (cross-cut) とは、\(V\) の部分集合 \(S\) であって \(\mathcal{P}\) を構成する任意の路が \(S\) の頂点をちょうど一つ含むものを言う。
この定義を使うと、定理 10.2.6 は「独立な横断カットを持つ \(D\) の路被覆が存在する」と表現できる。
定理 10.2.6 を証明するには、より強い次の命題を証明できれば十分である:
路被覆の要素数は路の個数を意味する点に注意してほしい。つまり、要素数最小の \(D\) の路被覆は路の個数が最も少ない路被覆を意味する。
これから示すのは Claim 1 よりさらに強い命題である。その命題を表明するには追加で用語が必要になる:
-
\(\mathcal{P}\) と路被覆とする。\(\mathcal{P}\) を構成する路の終点からなる集合を \(\operatorname*{Ends}\mathcal{P}\) と表記する。ここで \(\left\vert \operatorname*{Ends}\mathcal{P}\right\vert =\left\vert \mathcal{P}\right\vert \) に注意する。
-
\(\mathcal{P}\) を路被覆とする。\(\mathcal{P}\) が終端最小 (end-minimal) とは、路被覆 \(\mathcal{Q}\) で \(\operatorname*{Ends}\mathcal{Q}\) が \(\operatorname*{Ends}\mathcal{P}\) の真部分集合となるものが存在しないことを言う。
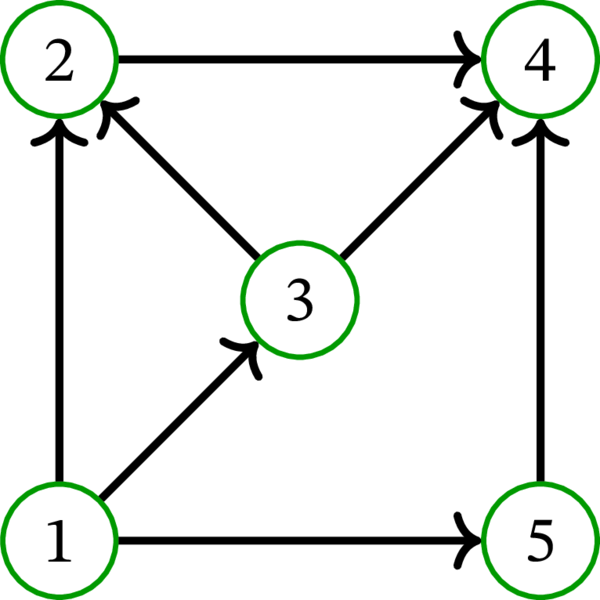
例 10.2.4 の有向グラフを \(D\) とする。先述した三つの路被覆を \(\mathcal{P}\), \(\mathcal{Q}\), \(\mathcal{R}\) と定める:
このとき次の等式が成り立つ:
ここから、\(\mathcal{Q}\) と \(\mathcal{R}\) は終端最小でないと分かる (\(\operatorname*{Ends}\mathcal{P}\) が \(\operatorname*{Ends}\mathcal{Q}\) と \(\operatorname*{Ends}\mathcal{R}\) の真部分集合であるため)。\(\mathcal{P}\) が終端最小 (かつ要素数最小) であることは容易に分かる。
一般のケースに戻る。明らかに、\(D\) の要素数最小の路被覆は終端最小でもある1。よって、次の命題は Claim 1 より強い:
これから Claim 2 を証明する2。
[Claim 2 の証明: \(\left\vert V\right\vert \) に関する数学的帰納法を用いる。
ベースケース: \(\left\vert V\right\vert =0\) のとき Claim 2 は明らかである (独立な横断カット \(\varnothing\) が存在するため)。
再帰ステップ: \(\left\vert V\right\vert =N\) を満たす多重有向グラフ \(D=\left( V,A,\psi\right) \) を考える。\(N-1\) 個の頂点を持つ多重有向グラフに対する Claim 2 が証明されていると (帰納法の仮定として) 仮定する。
\(D\) の終端最小な路被覆を \(\mathcal{P}\) とする。\(\mathcal{P}\) が独立な横断カットを持つと示せばよい。
\(\mathcal{P}\) を構成する路を \(\mathbf{p}_{1},\mathbf{p}_{2},\ldots,\mathbf{p}_{k}\) とする。\(\mathbf{p}_{1},\mathbf{p}_{2},\ldots,\mathbf{p}_{k}\) の終点をそれぞれ \(v_{1},v_{2},\ldots,v_{k}\) とする。このとき \(\left\{ v_{1},v_{2},\ldots ,v_{k}\right\} =\operatorname*{Ends}\mathcal{P}\) と \(k=\left\vert \operatorname*{Ends}\mathcal{P}\right\vert \) が成り立つ。
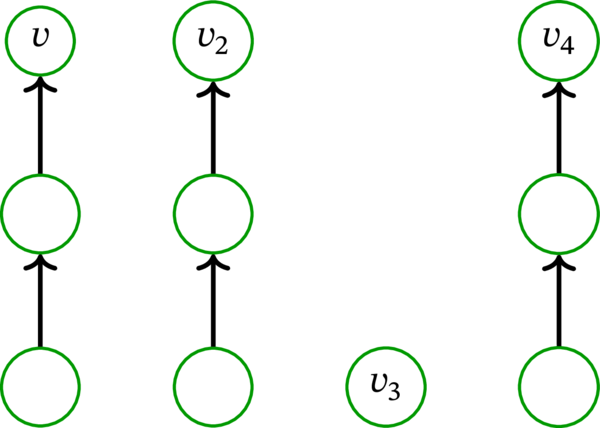
\(\mathcal{P}\) の独立な横断カットを見つけたいのだった。もし集合 \(\left\{ v_{1},v_{2},\ldots,v_{k}\right\} \) が独立なら、それが \(\mathcal{P}\) の独立な横断カットとなる。よって一般性を失うことなく \(v_{i}\) から \(v_{j}\) への弧が存在すると仮定する。\(D\) はループレスなので、\(v_{i}\) と \(v_{j}\) は異なる。路 \(\mathbf{p}_{1},\mathbf{p}_{2},\ldots,\mathbf{p}_{k}\) の順序は好きに変えて構わないから、一般性を失うことなく \(i=2\), \(j=1\) と仮定する。つまり、始点 \(v_{2}\) と終点 \(v_{1}\) を持つ弧の存在を仮定する。この弧を青い弧 (blue arc) と呼ぶ。\(\mathbf{p}_{1},\mathbf{p}_{2},\ldots,\mathbf{p}_{k}\) と青い弧の例を次の図に示す3:
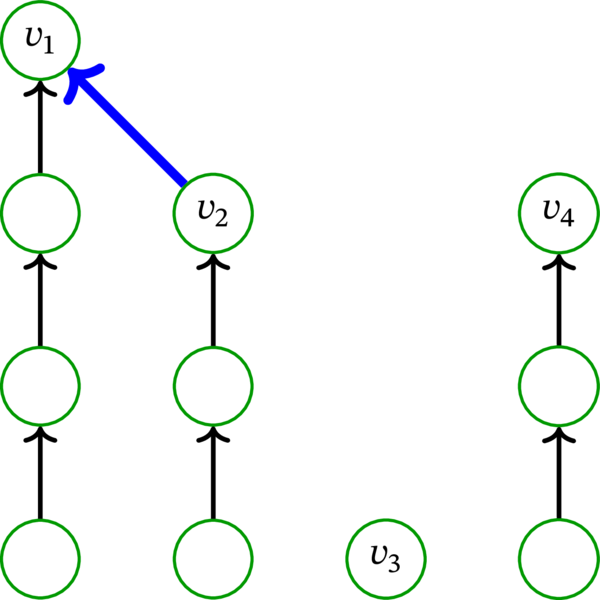
青い弧と頂点 \(v_{1}\) を \(\mathbf{p}_{2}\) の末尾に追加すると、\(\mathbf{p}_{2}\) より長い路が得られる。この路を \(\mathbf{p}_{2}+v_{1}\) と表記する。\(\mathbf{p}_{2}+v_{1}\) の終点は \(v_{1}\) である。
もし \(v_{1}\) が路 \(\mathbf{p}_{1}\) の唯一の頂点である (つまり、路 \(\mathbf{p}_{1}\) の長さが \(0\) である) なら、\(\mathbf{p}_{2}\) を \(\mathbf{p}_{2}+v_{1}\) で置き換え、長さ \(0\) の路 \(\mathbf{p}_{1}\) を路被覆 \(\mathcal{P}\) から除去することで、新しい路被覆 \(\mathbf{Q}\) が得られる。このとき \(\operatorname*{Ends}\mathcal{Q}\) は \(\operatorname*{Ends}\mathcal{P}\) の真部分集合となるものの、\(\mathcal{P}\) は終端最小よりこれは起こりえない。よって、\(\mathbf{p}_{1}\) は \(v_{1}\) 以外にも頂点を持つ。
そこで、\(\mathbf{p}_{1}\) の最後から二番目の (\(v_{1}\) の直前の) 頂点を \(v\) とする。このとき路 \(\mathbf{p}_{1}\) は始点 \(v\) と終点 \(v_{1}\) を持つ弧を含む。この弧を赤い弧 (red arc) と呼ぶ。赤い弧の例を次に示す:
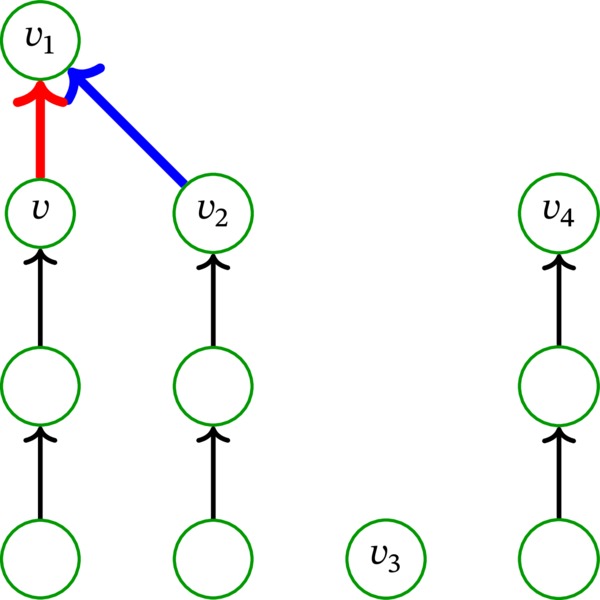
有向グラフ \(D\setminus v_{1}\) (始点または終点に \(v_{1}\) を持つ弧と頂点 \(v_{1}\) を \(D\) から除去して得られるグラフ) を \(D^{\prime}\) とする。\(\mathbf{p}_{1}\) から頂点 \(v_{1}\) と赤い弧を除去して得られる路を \(\mathbf{p}_{1}^{\prime}\) とする。このとき \(\mathcal{P}^{\prime}\colonequals \left\{ \mathbf{p}_{1}^{\prime},\mathbf{p}_{2},\mathbf{p}_{3},\ldots,\mathbf{p}_{k}\right\} \) は \(D^{\prime}\) の路被覆である。ここで \(\mathbf{p}_{1}^{\prime}\) の終点は \(v\) (\(\mathbf{p}_{1}\) の最後から二番目の頂点) であり、\(\mathbf{p}_{2},\mathbf{p}_{3},\ldots ,\mathbf{p}_{k}\) の終点は \(v_{2},v_{3},\ldots,v_{k}\) である。ここから \(\operatorname*{Ends} \mathcal{P}^{\prime} =\left\{ v,v_{2},v_{3},\ldots,v_{k}\right\} \) を得る。有向グラフ \(D^{\prime}=D\setminus v_{1}\) の路被覆 \(\mathcal{P}^{\prime}\) の例を次に示す:
\(D^{\prime}\) の路被覆 \(\mathcal{P}^{\prime}\) に注目する。\(\mathcal{P}^{\prime}\) が独立な横断カットを持つなら、それで証明が終了する。なぜなら、その横断カットは元々の路被覆 \(\left\{ \mathbf{p}_{1},\mathbf{p}_{2},\ldots ,\mathbf{p}_{k}\right\} =\mathcal{P}\) の横断カットでもあるからである。有向グラフ \(D\) は \(\left\vert V\right\vert =N\) 個の頂点を持つので、有向グラフ \(D\setminus v_{1}\) は \(N-1\) 個の頂点を持つ。よって路被覆 \(\mathcal{P}^{\prime }\) が (\(D^{\prime}\) の路被覆として) 終端最小だと示せれば、帰納法の仮定から \(\mathcal{P}^{\prime }\) が独立な横断カットを持つと言える。
よって路被覆 \(\mathcal{P}^{\prime }\) が (\(D^{\prime}\) の路被覆として) 終端最小だと示せばよい。背理法で示す。\(\operatorname*{Ends} \mathcal{Q}^{\prime} \) が \(\operatorname*{Ends} \mathcal{P}^{\prime} \) の真部分集合であるような \(D^{\prime}\) の路被覆 \(\mathcal{Q}^{\prime}\) が存在すると仮定し、この \(\mathcal{Q}^{\prime}\) に注目する。背理法の仮定より次の包含関係が分かる4:
ここから \(\left\vert \operatorname*{Ends} \mathcal{Q}^{\prime } \right\vert < \left\vert \left\{ v,v_{2},v_{3},\ldots,v_{k}\right\} \right\vert =k\) を得る。
続いて、次の三つの場合を分けて考える:
Case 2: \(v\notin\operatorname*{Ends} \mathcal{Q}^{\prime} \) と \(v_{2}\in\operatorname*{Ends} \mathcal{Q}^{\prime} \) が成り立つ。
Case 3: \(v\notin\operatorname*{Ends} \mathcal{Q}^{\prime} \) と \(v_{2}\notin\operatorname*{Ends} \mathcal{Q}^{\prime} \) が成り立つ。
それぞれの場合で矛盾を導ける:
-
まず Case 1 を考える。\(v\in \operatorname*{Ends} \mathcal{Q}^{\prime} \) が成り立つから、ある路 \(\mathbf{p}\in\mathcal{Q}^{\prime}\) が終端 \(v\) を持つ。この \(\mathbf{p}\) の末尾に赤い辺と頂点 \(v_{1}\) を追加した路を \(\mathbf{p}+v_{1}\) とする。\(\mathcal{Q}^{\prime}\) の \(\mathbf{p}\) を \(\mathbf{p}+v_{1}\) に変更した集合 \(\mathcal{Q}\) は \(D\) の路被覆であり、加えて \(\operatorname*{Ends}\mathcal{Q}\) は \(\operatorname*{Ends}\mathcal{P}\) の真部分集合となる5。しかし、これは \(\mathcal{P}\) が終端最小である事実と矛盾する。つまり Case 1 では矛盾が得られる。
-
続いて Case 2 を考える。\(\operatorname*{Ends} \mathcal{Q}^{\prime} \subseteq\left\{ v,v_{2},v_{3},\ldots,v_{k}\right\} \) と \(v\notin\operatorname*{Ends} \mathcal{Q}^{\prime} \) から次が分かる:
\[ \operatorname*{Ends} \mathcal{Q}^{\prime} \subseteq\left\{v,v_{2},v_{3},\ldots,v_{k}\right\} \setminus\left\{ v\right\} =\left\{v_{2},v_{3},\ldots,v_{k}\right\} \]\(v_{2}\in\operatorname*{Ends} \mathcal{Q}^{\prime} \) より、ある路 \(\mathbf{p}\in\mathcal{Q}^{\prime}\) が \(v_{2}\) で終わると分かる。この路 \(\mathbf{p}\) の末尾に青い辺と頂点 \(v_{1}\) に追加した路を \(\mathbf{p}+v_{1}\) とする。\(\mathcal{Q}^{\prime}\) の \(\mathbf{p}\) を \(\mathbf{p}+v_{1}\) に変更した集合 \(\mathcal{Q}\) は \(D\) の路被覆であり、加えて \(\operatorname*{Ends}\mathcal{Q}\) は \(\operatorname*{Ends}\mathcal{P}\) の真部分集合となる6。しかし、これは \(\mathcal{P}\) が終端最小である事実と矛盾する。つまり Case 2 では矛盾が得られる。
-
最後に Case 3 を考える。\(v\notin\operatorname*{Ends}\left( \mathcal{Q}^{\prime}\right) \) かつ \(v_{2}\notin\operatorname*{Ends}\left( \mathcal{Q}^{\prime}\right) \) であり、さらに \(\operatorname*{Ends}\left( \mathcal{Q}^{\prime}\right) \subseteq\left\{ v,v_{2},v_{3},\ldots,v_{k}\right\} \) が成り立つので、次が分かる:
\[ \operatorname*{Ends}\left( \mathcal{Q}^{\prime}\right) \subseteq\left\{v,v_{2},v_{3},\ldots,v_{k}\right\} \setminus\left\{ v,v_{2}\right\}=\left\{ v_{3},v_{4},\ldots,v_{k}\right\} \]ここから \(\left\vert \operatorname*{Ends}\left( \mathcal{Q}^{\prime}\right) \right\vert \leq\left\vert \left\{ v_{3},v_{4},\ldots,v_{k}\right\} \right\vert =k-2\) を得る。自明な路 \(\left( v_{1}\right) \) を \(\mathcal{Q}^{\prime}\) に加えて得られる集合 \(\mathcal{Q}\) は \(D\) の路被覆であり、加えて \(\operatorname*{Ends}\mathcal{Q}\) は \(\operatorname*{Ends}\mathcal{P}\) の真部分集合である7。しかし、これは \(\mathcal{P}\) が終端最小である事実と矛盾する。つまり Case 3 では矛盾が得られる。
三つの場合のそれぞれで矛盾が得られたので、仮定は偽である。つまり \(\mathcal{P}^{\prime}\) は終端最小だと分かる。先述したように、帰納法の仮定を \(D^{\prime}\) に適用すれば、\(D^{\prime}\) の終端最小な路被覆 \(D^{\prime}\) が独立な横断カットを持つと結論できる。この独立な横断カットは明らかに \(\mathcal{P}\) の独立な横断カットでもあるから、\(\mathcal{P}\) は独立な横断カットを持つ。以上で Claim 2 は証明された。]
先述したように、定理 10.2.6 は Claim 2 から従う。□
10.2.3応用
Gallai–Milgram の定理の簡単な応用を二つ紹介する:
-
遠い昔に証明した弱い Rédei の定理 (定理 4.10.6) を思い出してほしい。この定理は任意のトーナメントがハミルトン路を持つと主張する。この定理は Gallai–Milgram の定理を使って証明できる:
\(D\) をトーナメントとする。Gallai–Milgram の定理によれば、独立な横断カット8を持つ \(D\) の路被覆が存在する。この路被覆と横断カットに注目する。\(D\) はトーナメントだから、\(D\) の任意の独立集合は要素数が \(1\) 以下である。つまり、先述の路被覆は要素を一つしか持たない (路被覆とその横断カットは同じ個数の要素を持つため)。よって、この路被覆に属する唯一の路はハミルトン路である。以上で弱い Rédei の定理は (もう一度) 証明された。□
-
これより自明でない応用として、Hall の結婚定理 (定理 8.3.4) と Hall–König のマッチング定理 (定理 8.4.7) は Gallai–Milgram の定理を使って証明できる:
\(\left( G,X,Y\right) \) を二部グラフとする。
\(G\) の各辺を \(X\) から \(Y\) に向き付けることで得られる有向グラフを \(D\) とする (つまり、\(x \in X\) と \(y \in Y\) を端点に持つ \(G\) の辺に対応して \(D\) には始点 \(x\) と終点 \(y\) を持つ弧が存在する)。このとき弧の始点であり弧の終点でもあるような \(D\) の頂点は存在しない。よって \(D\) の任意の路は長さが \(1\) 以下だと分かる。二部グラフ \(\left( G,X,Y\right) \) と、それに対応する有向グラフ \(D\) の例を次に示す。例 8.2.2 で説明した方法で描画されている:
上述したように、\(D\) の任意の路は長さが \(1\) 以下である。よって \(D\) の任意の路は \(G\) の頂点または \(G\) の辺に (路の長さが \(0\) なら頂点に、長さが \(1\) なら辺に) 対応する。よって \(D\) の任意の路被覆 \(\mathcal{P}\) は長さが \(0\) の路 (\(G\) の頂点に対応する) と長さが \(1\) の路 (\(G\) の辺に対応する) からなる。さらに、\(\mathcal{P}\) の辺 (\(\mathcal{P}\) に属する長さが \(1\) の路に対応する辺) は \(G\) のマッチングを構成し、そのマッチングに属さない \(D\) の頂点は \(\mathcal{P}\) の頂点 (\(\mathcal{P}\) に属する長さが \(0\) の路に対応する頂点) に等しい。
定理 10.2.6 によれば、独立な横断カット \(S\) を持つ \(D\) の路被覆 \(\mathcal{P}\) が存在する。先ほどの例における \(\mathcal{P}\) と \(S\) の一例を次の図に示す。赤い弧が \(\mathcal{P}\) に属する長さが \(1\) の路を表し、青い四角が \(\mathcal{P}\) の独立な横断カット \(S\) を表す:
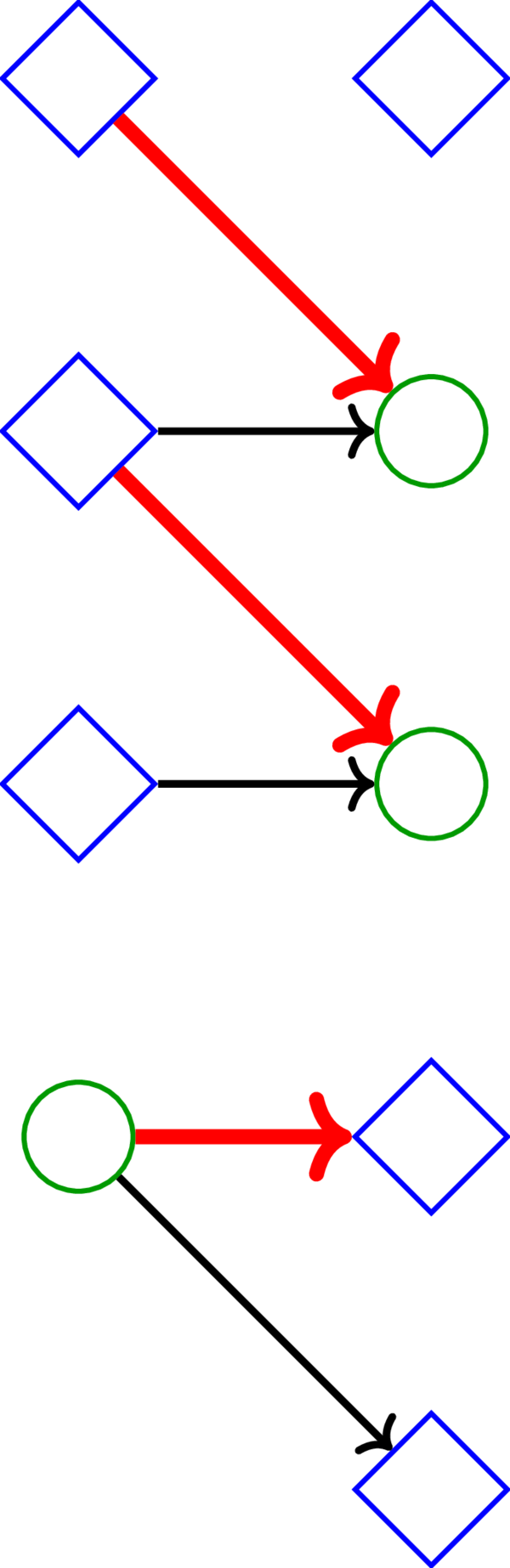
ここで \(\left\vert S\right\vert =\left\vert X\cap S\right\vert +\left\vert Y\cap S\right\vert \) が成り立つ (\(S\) は共通の要素を持たない二つの集合 \(X\cap S\) と \(Y\cap S\) の和集合であるため)。
集合 \(S\) は有向グラフ \(D\) の独立集合だから、\(D^{\operatorname*{und}}=G\) の独立集合でもある。これと \(\left( G,X,Y\right) \) が二部グラフである事実から \(N\left( X\cap S\right) \subseteq Y\setminus S\) を得る9。よって \(\left\vert N\left( X\cap S\right) \right\vert \leq\left\vert Y\setminus S\right\vert \) であり、\(\left\vert Y\setminus S\right\vert \geq\left\vert N\left( X\cap S\right) \right\vert \) が成り立つ。ここから次を得る:
\[ \begin{aligned} \left\vert Y\right\vert & =\underbrace{\left\vert Y\setminus S\right\vert }_{\geq\left\vert N\left( X\cap S\right) \right\vert }+\left\vert Y\cap S\right\vert \\ & \geq\left\vert N\left( X\cap S\right) \right\vert +\underbrace{\left\vert Y\cap S\right\vert }_{\substack{=\left\vert S\right\vert -\left\vert X\cap S\right\vert \\[3pt](\because\ \left\vert S\right\vert =\left\vert X\cap S\right\vert +\left\vert Y\cap S\right\vert )}}\nonumber\\ & =\left\vert N\left( X\cap S\right) \right\vert +\left\vert S\right\vert -\left\vert X\cap S\right\vert \qquad (1) \end{aligned} \]路被覆 \(\mathcal{P}\) に属する長さが \(1\) の路に対応する \(G\) の辺全体からなる集合を \(M\) とする。先述したように \(M\) は \(G\) のマッチングである (\(M\) に属する任意の二つの路は共通の頂点を持たないため)。\(M\) でマッチ済みでない頂点は、\(\mathcal{P}\) で任意の長さ \(1\) の路に属さない頂点に等しい。言い換えれば、それらは \(\mathcal{P}\) を構成する長さ \(0\) の路に属する (\(\mathcal{P}\) は \(D\) の路被覆であり、\(D\) の任意の路は長さが \(1\) 以下であるため)。\(M\) でマッチ済みでない \(X\) に属する頂点の個数を \(p\) として、\(M\) でマッチ済みでない \(Y\) に属する頂点の個数を \(q\) とする。
このとき、路被覆 \(\mathcal{P}\) は長さが \(0\) の個をちょうど \(p+q\) 個含む。具体的に言えば、\(\mathcal{P}\) は \(X\) に属する頂点一つからなる路を \(p\) 個、\(Y\) に属する頂点一つからなる路を \(q\) 個持つ。よって \(\mathcal{P}\) は \(\left\vert M\right\vert +p+q\) 個の路から構成される (長さが \(1\) の路は \(\left\vert M\right\vert \) 個あるため)。集合 \(S\) は \(\mathcal{P}\) の横断カットだから、\(\left\vert M\right\vert +p+q\) 個の路のそれぞれに属する頂点をちょうど一つずつ含む。よって次の等式が分かる:
\[ \left\vert S\right\vert =\left\vert M\right\vert +p+q \qquad (2) \]\(M\) でマッチ済みの任意の頂点 \(y \in Y\) はちょうど一つの \(M\)-辺に属する。逆に、任意の \(M\)-辺は \(Y\) に属する頂点をちょうど一つ含む。よって次の写像は全単射である:
\[ \begin{aligned} \left\{ M \text{ でマッチ済みの } Y \text{ に属する頂点} \right\} & \rightarrow M\\ y & \mapsto\left( y \text{ の }M\text{-辺}\right) \end{aligned} \]よって bijection principle より次の等式が分かる:
\[ \begin{aligned} \left(\text{\# } M \text{ でマッチ済みの } Y \text{ に属する頂点} \right) =\left\vert M\right\vert \end{aligned} \]一方、集合 \(Y\) は \(M\) でマッチ済みでない頂点をちょうど \(q\) 個含む (\(q\) の定義より)。よって \(Y\) は \(M\) でマッチ済みの頂点をちょうど \(\left\vert Y\right\vert -q\) 個含む。言い換えれば、次の等式が成り立つ:
\[ \left(\text{\# } M \text{ でマッチ済みの } \text{ Y に属する頂点} \right) =\left\vert Y\right\vert -q \]二つの等式を比較すれば \(\left\vert M\right\vert =\left\vert Y\right\vert -q\) を得る。言い換えれば、次の等式を得る:
\[ \left\vert M\right\vert +q=\left\vert Y\right\vert \qquad (3) \]\(Y\) と \(q\) の代わりに \(X\) と \(p\) に対して同じ議論を適用すれば、次の等式が分かる:
\[ \left\vert M\right\vert +p=\left\vert X\right\vert \qquad (4) \]これまでに示してきた式を使えば、式 \((3)\) を次のように変形できる:
\[ \begin{aligned} \left\vert M\right\vert +q & =\left\vert Y\right\vert \\ & \geq\left\vert N\left( X\cap S\right) \right\vert +\underbrace{\left\vert S\right\vert }_{\substack{=\left\vert M\right\vert +p+q\\[3pt]\text{(式 (2) より)}}}-\left\vert X\cap S\right\vert \ \ \ \ \ \ \ \ \ \ \left(\text{式 (1) より}\right) \\ & =\left\vert N\left( X\cap S\right) \right\vert +\left\vert M\right\vert +p+q-\left\vert X\cap S\right\vert \\ & =\underbrace{\left\vert M\right\vert +p}_{\substack{=\left\vert X\right\vert \\\text{(式 (4) より)}}}+\left\vert N\left( X\cap S\right) \right\vert -\left\vert X\cap S\right\vert +q\\ & =\left\vert X\right\vert +\left\vert N\left( X\cap S\right) \right\vert -\left\vert X\cap S\right\vert +q \end{aligned} \]両辺から \(q\) を引けば次を得る:
\[ \begin{aligned} \left\vert M\right\vert & \geq\left\vert X\right\vert +\left\vert N\left( X\cap S\right) \right\vert -\left\vert X\cap S\right\vert \nonumber\\ & =\left\vert N\left( X\cap S\right) \right\vert +\left\vert X\right\vert -\left\vert X\cap S\right\vert \qquad (5) \end{aligned} \]よって \(G\) のマッチング \(M\) と \(X\) の部分集合 \(U\) (\(= X\cap S\)) であって \(\left\vert M\right\vert \geq\left\vert N\left( U\right) \right\vert +\left\vert X\right\vert -\left\vert U\right\vert \) を満たすものが見つかったので、Hall–König のマッチング定理は (もう一度) 証明された。□
二部グラフ \(\left( G,X,Y\right) \) が Hall 条件を満たす (\(X\) の任意の部分集合 \(A\) が \(\left\vert N\left( A\right) \right\vert \geq\left\vert A\right\vert \) を満たす) と仮定する。先ほど Hall–König のマッチング定理の証明で示した議論から式 \((5)\) が分かる。さらに Hall 条件から、式 \((5)\) を次のように変形できる:
\[ \left\vert M\right\vert \geq\underbrace{\left\vert N\left( X\cap S\right) \right\vert }_{\geq\left\vert X\cap S\right\vert }+\left\vert X\right\vert-\left\vert X\cap S\right\vert \geq\left\vert X\right\vert \]よって命題 8.3.1 (e) よりマッチング \(M\) は \(X\)-完全である。つまり \(G\) は \(X\)-完全なマッチング \(M\) を持つ。以上で Hall の結婚定理は (もう一度) 証明された。□
\(c\) と \(r\) を正整数、\(r^{c}\) 個より多い頂点を持つトーナメントを \(T\) とする。\(T\) の各弧が \(c\) 個の色 \(1,2,\ldots,c\) のいずれかで塗られているとき、長さ \(r\) の単色な路が \(T\) に存在すると示せ。
練習問題 10.4 で \(c=1\) とすれば弱い Rédei の定理 (定理 4.10.6) が得られる。実際、任意のトーナメント \(T\) の各弧に色 \(1\) を割り当て、そこに練習問題 10.4 の命題を \(c=1\) および \(r=\left\vert \operatorname*{V}\left( T\right) \right\vert -1\) として適用すれば、\(T\) は長さ \(\left\vert \operatorname*{V}\left( T\right) \right\vert -1\) の単色な路を持つと分かる。この条件を満たす路は \(T\) の全ての頂点を含むので、\(T\) のハミルトン路である。
-
証明: \(\mathcal{P}\) を要素数最小の \(D\) の路被覆とする。\(\mathcal{P}\) が終端最小でないなら、\(\left\vert \operatorname*{Ends}\mathcal{Q}\right\vert < \left\vert \operatorname*{Ends}\mathcal{P}\right\vert \) を満たす路被覆 \(\mathcal{Q}\) が存在する。このとき \(\left\vert \mathcal{Q}\right\vert =\left\vert \operatorname*{Ends}\mathcal{Q}\right\vert < \left\vert \operatorname*{Ends}\mathcal{P}\right\vert =\left\vert \mathcal{P}\right\vert \) であるものの、これは \(\mathcal{P}\) の要素数の最小性に反する。よって \(\mathcal{P}\) は終端最小である。 ↩︎
-
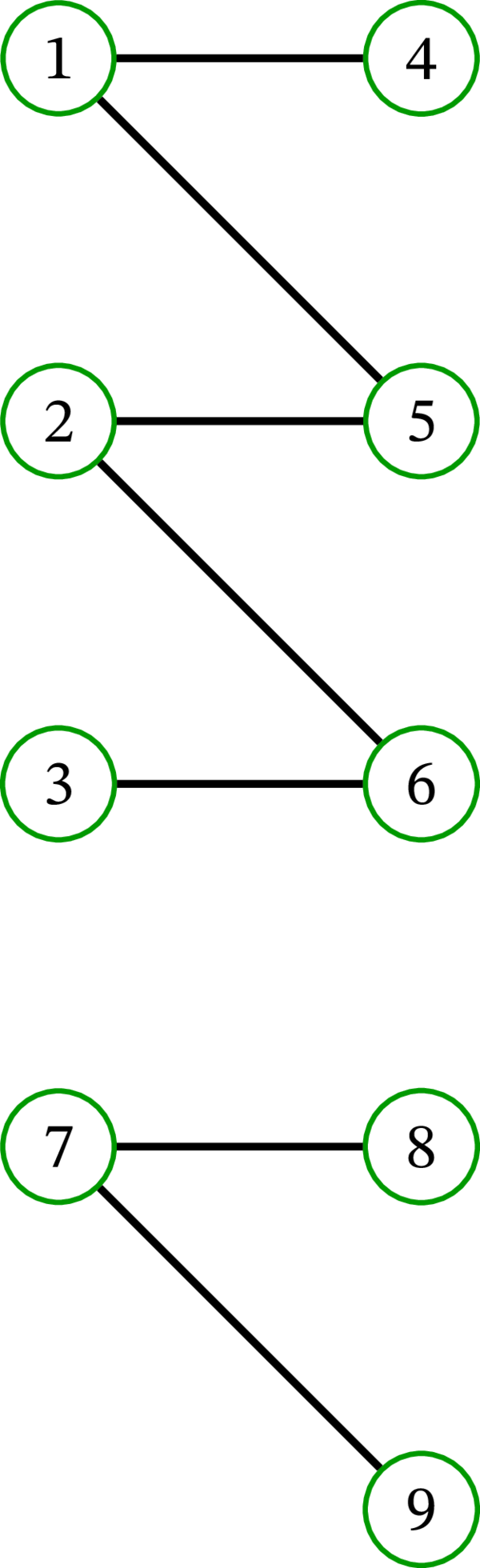
余談: Claim 2 は本当に Claim 1 より強いのだろうか? この質問の答えは「Yes」である: 終端最小の路被覆が要素数最小でないことがあり得る。例えば、次の有向グラフを \(D\) とする:
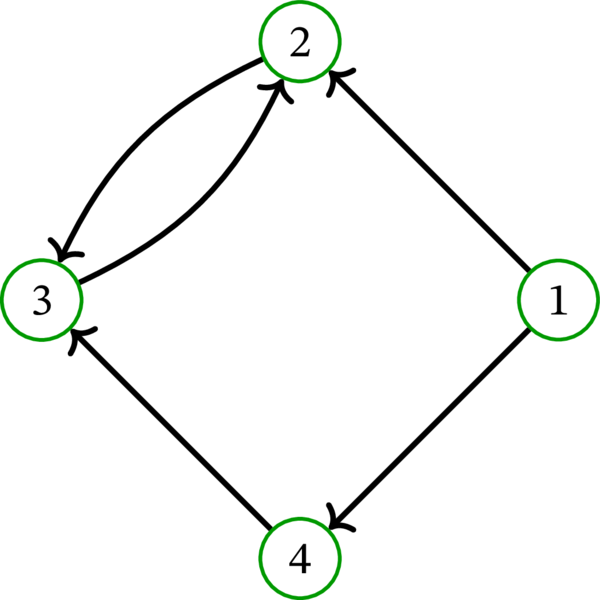
このとき \(D\) の路被覆 \(\left\{ \left( 1,\ast,2,\ast,3\right) ,\ \left( 4\right) \right\} \) は終端最小であるものの、要素数最小ではない。 ↩︎
-
この図は \(k=4\) のケースを示している。四つの列が四つの路を表し、左から右にそれぞれ \(\mathbf{p}_{1},\mathbf{p}_{2},\mathbf{p}_{3},\mathbf{p}_{4}\) に対応する。有向グラフ \(D\) が図にあるより多くの弧を持つ可能性は当然あるものの、今の議論ではそれらを考えていない。 ↩︎
-
記号 \(\subsetneq\) は「真部分集合である」を意味する。斜線は横線だけに交わり、上の曲線とは交わらない。 ↩︎
-
証明: \(\mathcal{Q}^{\prime}\) の \(\mathbf{p}\) を \(\mathbf{p}+v_{1}\) に置き換えて得られるのが \(\mathbf{Q}\) である。この置き換えによって、\(\operatorname*{Ends}\mathcal{Q^{\prime}}\) に含まれる \(\mathbf{p}\) の終点 \(v\) は \(\operatorname*{Ends}\mathcal{Q}\) で \(\mathbf{p}+v_{1}\) の終点 \(v_{1}\) に置き換わる。ここから次が分かる:
\[ \begin{aligned} \operatorname*{Ends}\mathcal{Q} & =\underbrace{\left( \operatorname*{Ends} \mathcal{Q}^{\prime} \setminus\left\{ v\right\} \right) }_{\substack{\subseteq\left\{ v_{2},v_{3},\ldots,v_{k}\right\} \\[3pt]\ (\because\ \operatorname*{Ends} \mathcal{Q}^{\prime} \subseteq\left\{ v,v_{2},v_{3},\ldots,v_{k}\right\})}}\cup\left\{ v_{1}\right\} \\ & \subseteq\left\{ v_{2},v_{3},\ldots,v_{k}\right\} \cup\left\{ v_{1}\right\} =\left\{ v_{1},v_{2},\ldots,v_{k}\right\} =\operatorname*{Ends}\mathcal{P} \end{aligned} \]同じ理由で \(\left\vert \operatorname*{Ends}\mathcal{Q}\right\vert =\left\vert \operatorname*{Ends} \mathcal{Q}^{\prime } \right\vert < k=\left\vert \operatorname*{Ends}\mathcal{P}\right\vert \) であり、ここから \(\operatorname*{Ends}\mathcal{Q}\neq\operatorname*{Ends}\mathcal{P}\) を得る。これと \(\operatorname*{Ends}\mathcal{Q}\subseteq\operatorname*{Ends}\mathcal{P}\) より、\(\operatorname*{Ends}\mathcal{Q}\) は \(\operatorname*{Ends}\mathcal{P}\) の真部分集合だと結論できる。 ↩︎
-
証明: \(\mathcal{Q}^{\prime}\) の \(\mathbf{p}\) を \(\mathbf{p}+v_{1}\) に置き換えて得られるのが \(\mathcal{Q}\) である。この置き換えによって、\(\operatorname*{Ends}\mathcal{Q^{\prime}}\) に含まれる \(\mathbf{p}\) の終点 \(v_{2}\) は \(\operatorname*{Ends}\mathcal{Q}\) で \(\mathbf{p}+v_{1}\) の終点 \(v_{1}\) に置き換わる。ここから次が分かる:
\[ \begin{aligned} \operatorname*{Ends}\mathcal{Q} & =\underbrace{\left( \operatorname*{Ends} \mathcal{Q}^{\prime} \setminus\left\{ v_{2}\right\} \right) }_{\substack{\subseteq\left\{ v_{3},v_{4},\ldots,v_{k}\right\} \\[3pt] (\because\ \operatorname*{Ends} ( \mathcal{Q}^{\prime} ) \subseteq\left\{ v_{2},v_{3},\ldots,v_{k}\right\})}}\cup\left\{ v_{1}\right\} \\ & \subseteq\left\{ v_{3},v_{4},\ldots,v_{k}\right\} \cup\left\{ v_{1}\right\} =\left\{ v_{1},v_{3},v_{4},\ldots,v_{k}\right\} \\ & \subsetneq\left\{ v_{1},v_{2},\ldots,v_{k}\right\} =\operatorname*{Ends}\mathcal{P} \end{aligned} \]言い換えれば、\(\operatorname*{Ends}\mathcal{Q}\) は \(\operatorname*{Ends}\mathcal{P}\) の真部分集合である。 ↩︎
-
証明: \(\mathcal{Q}^{\prime}\) に自明な路 \(\left( v_{1}\right) \) を追加して得られるのが \(\mathcal{Q}\) である。追加された自明な路の終点は \(v_{1}\) なので、次が分かる:
\[ \begin{aligned} \operatorname*{Ends}\mathcal{Q} & =\underbrace{\operatorname*{Ends}\left( \mathcal{Q}^{\prime}\right) }_{\subseteq\left\{ v_{3},v_{4},\ldots ,v_{k}\right\} }\cup\left\{ v_{1}\right\} \subseteq\left\{ v_{3},v_{4},\ldots,v_{k}\right\} \cup\left\{ v_{1}\right\} =\left\{ v_{1},v_{3},v_{4},\ldots,v_{k}\right\} \\ & \subsetneq\left\{ v_{1},v_{2},\ldots,v_{k}\right\} =\operatorname*{Ends}\mathcal{P} \end{aligned} \]言い換えれば、\(\operatorname*{Ends}\mathcal{Q}\) は \(\operatorname*{Ends}\mathcal{P}\) の真部分集合である。 ↩︎
-
証明: \(v\in N\left( X\cap S\right) \) を任意に取って固定する。\(v\) は \(X \cap S\) に属する隣接頂点を持つから、この条件を満たす \(v\) の隣接頂点を \(x\) とする。\(x\in X\cap S\subseteq X\) なので、\(v\) は \(X\) に属する隣接頂点 \(x\) を持つ。\(\left( G,X,Y\right) \) は二部グラフなので、ここから \(v \in Y\) が分かる。また、\(x\in X\cap S\subseteq S\) も分かる。もし \(v\in S\) だと、集合 \(S\) が隣接する二頂点 \(v\), \(x\) を含むことになり、\(S\) が \(G\) の独立集合である事実と矛盾する。よって \(v \notin S\) である。\(v \in Y\) と \(v \notin S\) より \(v\in Y\setminus S\) を得る。
\(v\) を固定したことを忘れる。以上で任意の \(v\in N\left( X\cap S\right) \) が \(v\in Y\setminus S\) を満たすことが証明された。言い換えれば \(N\left( X\cap S\right) \subseteq Y\setminus S\) である。 ↩︎