6.1. グラフの彩色の定義

これは真面目な数学の講義なので、色は正整数で表される。頂点に色を塗るとは、各頂点に正整数を割り当てることに等しい:

定義 6.1.1

\(G=\left( V,E,\varphi\right) \) を多重グラフ、\(k\) を自然数とする。

\(G\) の \(k\)-彩色 (\(k\)-coloring) とは、写像 \(f\colon V\rightarrow \left\{ 1,2,\ldots,k\right\} \) を意味する。\(k\)-彩色 \(f\) が与えられたとき、自然数 \(1,2,\ldots,k\) を色 (color) と呼び、\(f\left( v\right) \) を「\(k\)-彩色 \(f\) における頂点 \(v\) の色」と呼ぶ。
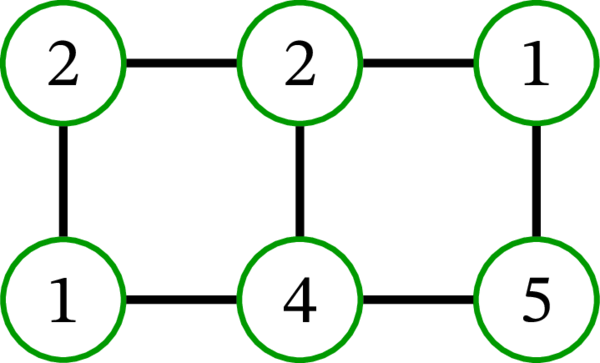
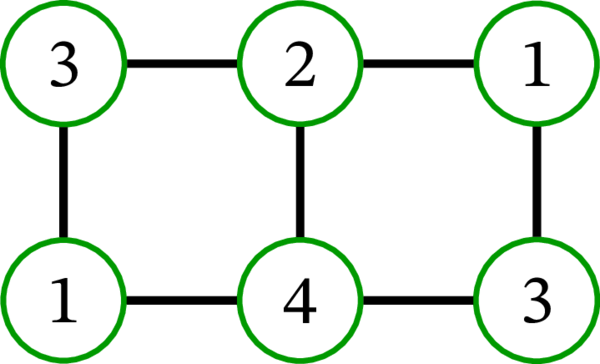
\(G\) の \(k\)-彩色 \(f\) が適切 (proper) とは、\(G\) で隣接する任意の二頂点が同じ色を持たないことを言う。 [言い換えれば、\(G\) の \(k\)-彩色 \(f\) が適切なのは、\(f\left( u\right) =f\left( v\right) \) を満たす \(u\), \(v\) を端点に持つ \(G\) の辺が存在しないとき、かつそのときに限る。]

例 6.1.2

同じグラフに対する二つの \(7\)-彩色を示す:

[円の内側に書かれた数字は頂点ではなく頂点の色を表す。] 左の \(7\)-彩色 (色 \(3\), \(6\), \(7\) は使われていないものの、\(7\)-彩色であることに変わりはない) では同じ色を持つ左上の頂点と中央上の頂点が隣接しているので、この彩色は適切でない。これに対して右の \(7\)-彩色は適切である。

例 6.1.3

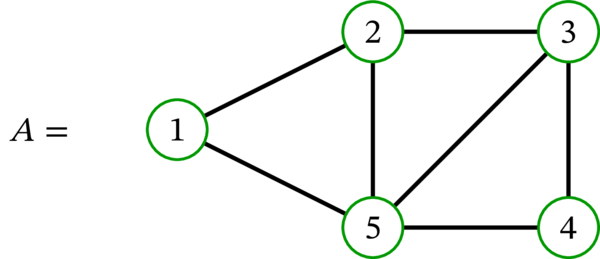
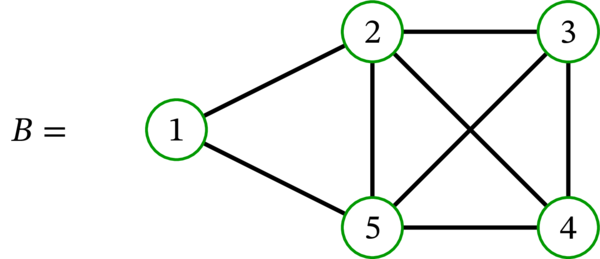
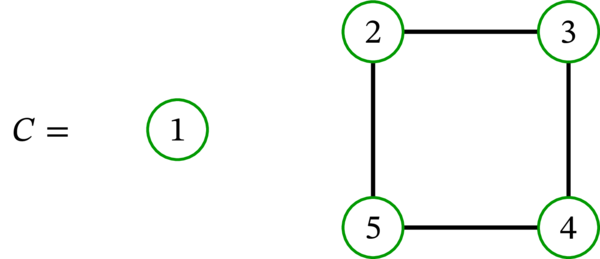
次に示すグラフの中で、適切な \(3\)-彩色を持つのはどれか？

グラフ \(A\) は適切な \(3\)-彩色を持つ。例えば、頂点 \(1,2,3,4,5\) をそれぞれ \(1,2,1,2,3\) に移す写像 \(f\) は適切な \(3\)-彩色となる。
グラフ \(B\) は適切な \(3\)-彩色を持たない。実際、四つの頂点 \(2\), \(3\), \(4\), \(5\) は相互に隣接するので、適切な \(k\)-彩色は \(4\) 個の色を必要とする。よって \(k\geq 4\) でなければならない。
グラフ \(C\) は適切な \(3\)-彩色を持つ。さらに、\(C\) は適切な \(2\)-彩色 (例えば、奇数の頂点に色 \(1\) を割り当て、偶数の頂点に色 \(2\) を割り当てる写像) も持つ。
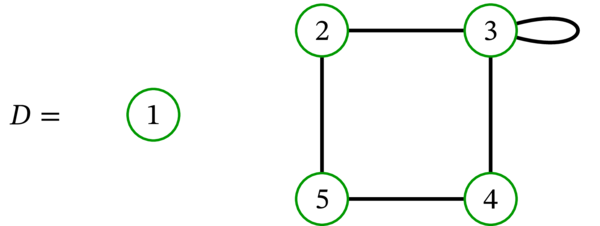
グラフ \(D\) は適切な \(3\)-彩色を持たない。さらに言えば、任意の \(k\in \mathbb{N}\) に対して \(D\) は適切な \(k\)-彩色を持たない。頂点 \(3\) がループを通じて自身と隣接するので、\(G\) の任意の \(k\)-彩色は適切とならない。一般的に言えば、ループを持つグラフは任意の \(k \in \mathbb{N}\) に対して適切な \(k\)-彩色を持たない。

例 6.1.4

\(n\) を自然数とする。\(n\) 次元超立方体グラフ \(Q_{n}\) (定義 2.14.7) は適切な \(2\)-彩色を持つ。具体的には、次の写像が \(Q_{n}\) の適切な \(2\)-彩色である:

\[ \begin{aligned} f\colon \left\{ 0,1\right\} ^{n} & \rightarrow\left\{ 1,2\right\} \\ \left( a_{1},a_{2},\ldots,a_{n}\right) & \mapsto \begin{cases} 1 & (a_{1}+a_{2}+\cdots+a_{n}\text{ が偶数のとき})\\ 2 & (a_{1}+a_{2}+\cdots+a_{n}\text{ が奇数のとき}) \end{cases} \end{aligned} \]

[確認せよ！二つのビット文字列 \(\left( a_{1},a_{2},\ldots,a_{n}\right) \) と \(\left( b_{1},b_{2},\ldots,b_{n}\right) \) がちょうど一箇所でだけ異なるとき、対応する和 \(a_{1}+a_{2}+\cdots+a_{n}\) と \(b_{1}+b_{2}+\cdots+b_{n}\) が \(1\) だけ異なることを示せばよい。]

例 6.1.5

\(n\), \(m\) を正整数とする。\(n\) 次の路グラフ \(P_{n}\) と \(m\) 次の路グラフ \(P_{m}\) のデカルト積 \(P_{n}\times P_{m}\) は、次に示す \( n \times m \) の格子グラフ (grid graph) である:

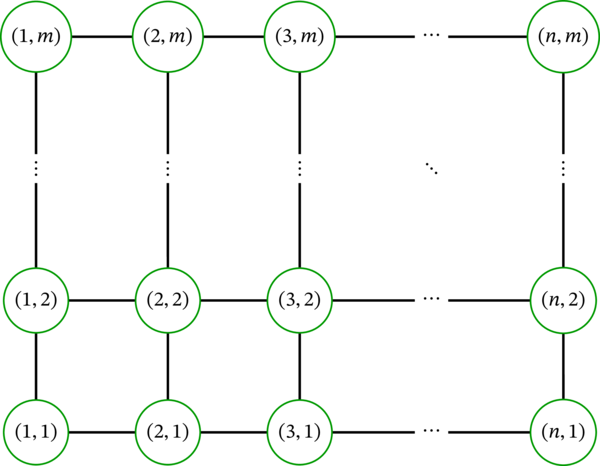
\( n \times m \) の格子グラフ \(P_{n}\times P_{m}\) は \(n\) と \(m\) の値に関わらず適切な \(2\)-彩色を持つ。具体的には、頂点 \(\left( i,j\right) \) を \(\begin{cases}1 & (i+j\text{ が奇数のとき})\\ 2 & (i+j\text{ が偶数のとき}) \end{cases}\) に対応付ける写像が \(P_{n}\times P_{m}\) の適切な \(2\)-彩色である。

この \(2\)-彩色は明らかな理由によりチェス盤彩色 (chessboard coloring) と呼ばれる (各頂点がチェス盤の格子となる)。

さらに一般的に言うと、単純グラフ \(G\), \(H\) が適切な \(2\)-彩色を持つとき、それらのデカルト積 \(G \times H\) も適切な \(2\)-彩色を持つ (証明は練習問題 6.4 で行う)。

例 6.1.6

第 2.6.3 項で定義した Petersen グラフを次に示す:

このグラフは適切な \(3\)-彩色を持つ。見つけられるだろうか？

ここまでの例から分かるように、適切な \(3\)-彩色を持つグラフもあれば持たないグラフもある。明らかに、相互に隣接する \(4\) 頂点が存在するなら適切な \(3\)-彩色は不可能になる (色が \(3\) 種類しかないとき、鳩の巣原理より同じ色で塗られる二頂点が必ず存在する)。しかし、この逆「適切な \(3\)-彩色が不可能なら相互に隣接する \(4\) 頂点が存在する」は成り立たない。グラフが適切な \(3\)-彩色を持つかどうかを判定する問題は NP 完全であることが知られている。