4.6. 有向グラフの強接続性と弱接続性
無向グラフの頂点に対する「路連結性」という関係は路の存在を使って定義された (定義 2.9.8)。しかし有向グラフでは、二頂点 \(u\), \(v\) に対する「\(u\) から \(v\) への歩道が存在する」と「\(v\) から \(u\) への歩道が存在する」が (一般に) 関係として等価でないので、路連結性が対称性を持たない。そのため、この関係を表すのに \(\simeq_{D}\) のような対称性を示唆する記号を使うのは避けたい。そこで、両方の歩道の存在を意味する強路連結性という関係を定義する:
\(D\) を多重有向グラフとする。集合 \(\operatorname*{V}\left( D\right) \) 上の二項関係 \(\simeq_{D}\) を次のように定義する: \(D\) の頂点 \(u\), \(v\) に対して、\(u\) から \(v\) への歩道と \(v\) から \(u\) への歩道が両方とも存在するとき、かつそのときに限って \(u\simeq_{D}v\) と定める。
この二項関係 \(\simeq_{D}\) を強路連結性 (strong path-connectedness) と呼ぶ。頂点 \(u\), \(v\) で \(u \simeq_{D} v\) が成り立つとき、\(u\) と \(v\) は強路連結 (strongly path-connected) と言う。
\(D\) を例 4.5.4 の多重グラフとする。\(D\) には \(1\) から \(2\) への歩道 \(\left( 1,a,2\right)\) と \(2\) から \(1\) への歩道 \(\left( 2,b,3,d,1\right)\) がどちらも存在するので \(1 \simeq_{D} 2\) が成り立つ。しかし \(3\simeq_{D}4\) は成り立たない。実際、\(D\) に \(3\) から \(4\) への歩道は存在するものの、\(4\) から \(3\) への歩道は存在しない。
\(D\) を多重有向グラフとする。関係 \(\simeq_{D}\) は同値関係である。
易しい。単純グラフの場合と同様に示せる。□
多重有向グラフにおいても、\(\simeq_{D}\) の定義にある「歩道」は「路」に置き換えることができる:
\(D\) を多重有向グラフ、\(u\) と \(v\) を \(D\) の頂点とする。このとき \(u\) から \(v\) への路と \(v\) から \(u\) への路が存在するとき、かつそのときに限って \(u\simeq_{D}v\) が成り立つ。
易しい。単純グラフの場合と同様に示せる。□
\(D\) を多重有向グラフとする。同値関係 \(\simeq_{D}\) の同値類を \(D\) の強成分 (strong component) と呼ぶ。
\(D\) を多重有向グラフとする。\(D\) の強成分がちょうど一つだけなら、\(D\) は強連結 (strongly connected) と言う。
つまり、多重有向グラフ \(D\) は「少なくとも一つの頂点を持つ」と「任意の頂点から任意の頂点への路が存在する」を満たすとき、かつそのときに限って強連結となる1。
これらの概念と対になる「弱い」接続性や接続成分も定義される:
\(D\) を多重有向グラフとする。台無向グラフ \(D^{\operatorname*{und}}\) の成分 (同値関係 \(\simeq_{D^{\operatorname*{und}}}\) の同値類) を \(D\) の弱成分 (weak component) と呼ぶ。\(D\) がちょうど一つの弱成分からなる (\(D^{\operatorname*{und}}\) が連結である) とき、\(D\) は弱連結 (weakly connected) と言う。
\(D\) を次の単純有向グラフとする:
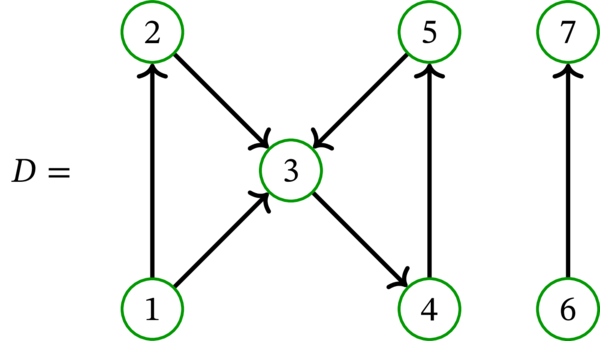
\(D\) を多重有向グラフ \(D^{\operatorname*{mult}}\) とみなすとき:
-
\(D\) の弱成分は \(\left\{ 1,2,3,4,5\right\} \) と \(\left\{ 6,7\right\} \) である。
-
\(D\) の強成分は \(\left\{ 1\right\} \), \(\left\{ 2\right\} \), \(\left\{ 3,4,5\right\} \), \(\left\{ 6\right\} \), \(\left\{ 7\right\} \) である。例えば \(1\not \simeq _{D}2\not \simeq _{D}3\) であるのに対して、\(3\simeq_{D}4\simeq_{D}5\) は成り立つ。
よって \(D\) は強連結でも弱連結でもない。また、\(D\) の強成分は弱成分より多い。
任意の強連結な有向グラフは弱連結である。
\(D\) を多重有向グラフとする。\(D\) における任意の歩道は \(D^{\operatorname*{und}}\) における歩道に等しい (正確に言えば、変換可能である)。よって、\(D\) の頂点 \(u\), \(v\) が \(D\) で強路連結なら、\(u\) と \(v\) は \(D^{\operatorname*{und}}\) で路連結でもある。よって \(D\) が強連結なら \(D^{\operatorname*{und}}\) は連結、すなわち \(D\) は弱連結である。□
\(D\) を多重有向グラフとする。\(D\) の強成分と \(D\) の弱成分が一致するのは、\(D\) の各辺が少なくとも一つの閉路に含まれるとき、かつそのときに限ると示せ。
双方向の向き付け (多重グラフ \(G\) を多重有向グラフ \(G^{\operatorname*{bidir}}\) に移す操作 \(G\mapsto G^{\operatorname*{bidir}}\)) が歩道・路・閉歩道・閉路に及ぼす影響を調べよう:
\(G\) を多重グラフとする。このとき:
-
\(G\) の歩道は多重有向グラフ \(G^{\operatorname*{bidir}}\) の歩道と「だいたい」同じになる。正確に言えば、\(G\) の任意の歩道からは (同じ始点と終点を持った) \(G^{\operatorname*{bidir}}\) の歩道を構築でき、逆に \(G^{\operatorname*{bidir}}\) の任意の歩道からは (同じ始点と終点を持った) \(G\) の歩道を構築できる。もし \(G\) がループを持たないなら、\(G\) の歩道と \(G^{\operatorname*{bidir}}\) の歩道の間には一対一の対応関係 (全単射) が存在する。
-
\(G\) の路は多重有向グラフ \(G^{\operatorname*{bidir}}\) の路と「だいたい」同じになる。路はループを含まないので、\(G\) の路と \(G^{\operatorname*{bidir}}\) の路の間には必ず一対一の対応関係が存在する。
-
\(G\) の閉歩道は多重有向グラフ \(G^{\operatorname*{bidir}}\) の閉歩道と「だいたい」同じになる。
-
\(G\) の閉路は \(G^{\operatorname*{bidir}}\) の閉路と同じにならない。実際、\(e\) を \(G\) の辺、\(u\), \(v\) を \(e\) の端点とするとき、\(\left( u,e,v,e,u\right) \) は \(G\) の閉路でない。しかし、\(\left( u,\left( e,1\right) ,v,\left( e,2\right) ,u\right) \) または \(\left( u,\left( e,2\right) ,v,\left( e,1\right) ,u\right) \) は \(G^{\operatorname*{bidir}}\) の閉路となる。図を見た方が分かりやすいだろう。\(G\) の辺 \(e\) と頂点 \(u\), \(v\) を次に示す:
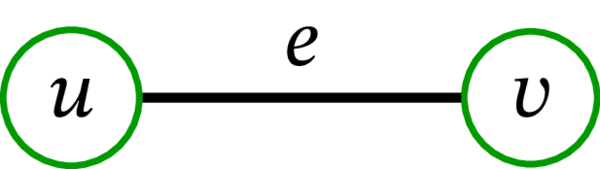
これに対応する \(G^{\operatorname*{bidir}}\) の辺と頂点の一例を次に示す:
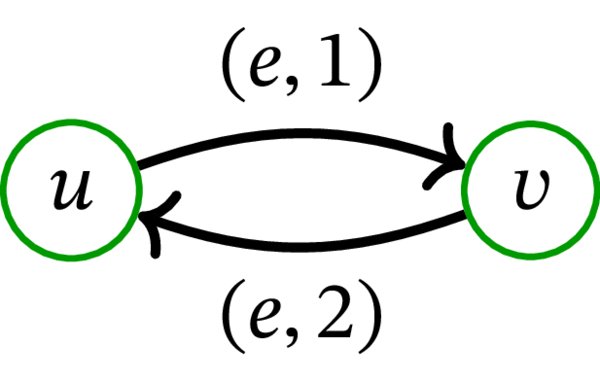
一般に \(G^{\operatorname*{bidir}}\) は \(G\) より多くの閉路を持つ。ただし、\(G\) の任意の閉路に対応する \(G^{\operatorname*{bidir}}\) の閉路が存在するのも確かである。
\(D=\left( V,E,\psi\right) \) を多重有向グラフとする。
\(A\), \(B\), \(C\) はどれも \(V\) の部分集合であり、誘導部分有向グラフ \(D\left[ A\right] \), \(D\left[ B\right] \), \(D\left[ C\right] \) がどれも強連結だとする。
\(D\) の閉路が少なくとも一つの \(D\left[ A\right] \) の弧、少なくとも一つの \(D\left[ B\right] \) の弧、そして少なくとも一つの \(D\left[ C\right] \) の弧を含むとき、その閉路を折衷的 (eclectic) と呼ぶことにする (条件にある三つ弧が異なることは要求されない)。
次の命題を証明せよ:
-
「三つの集合 \(B\cap C\), \(\,C\cap A\), \(\,A\cap B\) が全て非空」かつ「集合 \(A\cap B\cap C\) が空」なら \(D\) は折衷的な閉路を持つ。
-
「三つの誘導部分有向グラフ \(D\left[ B\cap C\right] \), \(\,D\left[ C\cap A\right] \), \(\,D\left[ A\cap B\right] \) が全て強連結」かつ「誘導部分有向グラフ \(D\left[ A\cap B\cap C\right] \) が強連結でない」なら \(D\) は折衷的な閉路を持つ。
-
「strongly connected」ではなく「diconnected」という単語を用いる文献もある。ただ、「diconnected」は「disconnected (非連結)」と一文字しか違わないので、この単語の使用を私は推奨しない。 ↩︎