4.4. 有向グラフへの変換
4.4.1多重有向グラフから多重グラフへの変換
任意の多重有向グラフ \(D\) は「矢印」を除去することで (無向) 多重グラフ \(G\) に変換できる。この操作を「弧の向きを無視する」と呼ぶこともある:
\(D\) を多重有向グラフとする。\(D\) の任意の弧 \(a\) を \(a\) の始点と終点を端点に持つ辺で置き換えることで得られる多重グラフを \(D^{\operatorname*{und}}\) と表記する。数学的に言えば、\(D^{\operatorname*{und}}\) は次のように定義できる: 多重有向グラフ \(D=\left( V,A,\psi\right) \) に対して \(D^{\operatorname*{und}}\colonequals \left( V,A,\varphi\right) \) と定める。ここで、写像 \(\varphi\colon A\rightarrow\mathcal{P}_{1,2}\left( V\right) \) は弧 \(a\in A\) のそれぞれを \(\psi\left( a\right) \) の要素からなる集合に移す (つまり、\(\varphi\left( a\right) \) は \(a\) の始点と \(a\) の終点からなる集合である)。
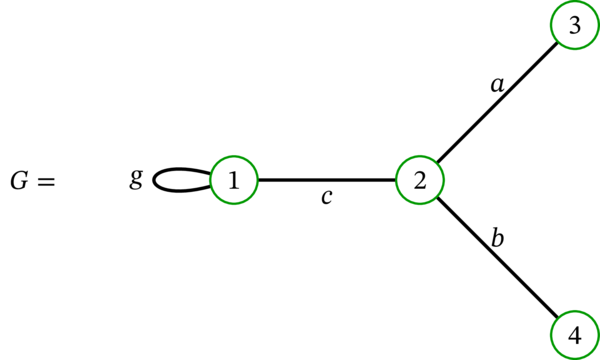
例えば、\(D\) が例 4.1.6 で示した多重有向グラフなら、\(D^{\operatorname*{und}}\) は次の多重グラフとなる:
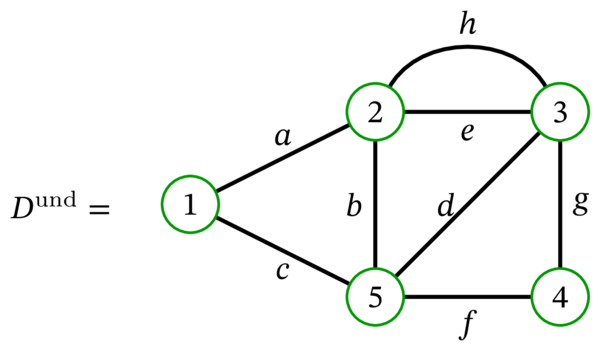
4.4.2多重グラフから多重有向グラフへの変換
弧の向きを無視することで任意の多重有向グラフ \(D\) を多重グラフ \(D^{\operatorname*{und}}\) に変換する方法を見た。
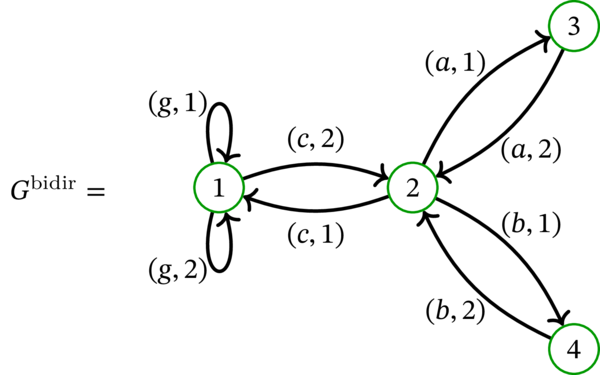
逆に、各辺を重複させる (正確には、逆方向を向いた二つの弧で各辺を置き換える) 操作を使えば多重グラフ \(G\) を多重有向グラフ \(G^{\operatorname*{bidir}}\) に変換できる:
\(G=\left( V,E,\varphi\right) \) を多重グラフとする。各辺 \(e \in E\) に対して端点を任意に一つ選び、それを \(s_{e}\) とする。\(e\) の \(s_{e}\) でない方の端点を \(t_{e}\) とする。もし \(e\) がループなら、\(t_{e}\) は \(s_{e}\) と同じ頂点と定める。
\(G^{\operatorname*{bidir}}\) を多重有向グラフ \(\left( V,\ \ E\times\left\{ 1,2\right\} ,\ \ \psi\right) \) と定める。ここで写像 \(\psi\colon E\times\left\{ 1,2\right\} \rightarrow V\times V\) は各 \(e \in E\) に対して次のように定義される:
写像 \(\psi\) が \(s_{e}\) の選択よって変わる点に注意してほしい。\(s_{e}\) として選択する辺 \(e\) の端点を変えると \(\psi\) も変化する。このため \(G^{\operatorname*{bidir}}\) の定義は一つに定まらない (正準な \(G^{\operatorname*{bidir}}\) は存在しない)。この曖昧性を除去する巧妙な工夫があるかもしれないが、著者は知らない。ただ幸い、\(s_{e}\) をどのように選択したとしても \(G^{\operatorname*{bidir}}\) は互いに同型なグラフとなる (多重有向グラフの「同型」は読者の想像するまさにその通りに定義される)。
次の多重有向グラフを \(G\) とする:
この \(G\) に対応する \(G^{\operatorname*{bidir}}\) を次に示す:
多重グラフ \(G\) に多重有向グラフ \(G^{\operatorname*{bidir}}\) を割り当てる操作は単射である ── つまり、多重有向グラフ \(G^{\operatorname*{bidir}}\) からは元々の多重グラフ \(G\) を一意に復元できる。これとは対照的に、操作 \(D\mapsto D^{\operatorname*{und}}\) は弧の向きという情報を消去するので単射でない。なお、多重グラフ \(\left( G^{\operatorname*{bidir}}\right) ^{\operatorname*{und}}\) は \(G\) と同型でないことに注意してほしい。\(\left( G^{\operatorname*{bidir}}\right) ^{\operatorname*{und}}\) では \(G\) の各辺が二つに増えている。
4.4.3単純有向グラフから多重有向グラフへの変換
続いて、さらに別の操作を定義する: 単純有向グラフを多重有向グラフに変換する操作である。これは単純グラフを多重グラフに変化する操作 \(G\mapsto G^{\operatorname*{mult}}\) に非常によく似ているので、記号も同じものを用いる。その定義は次の通りである:
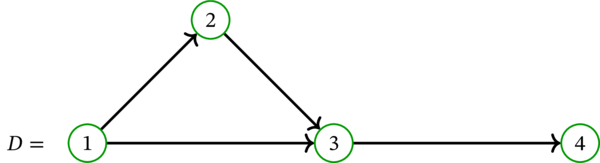
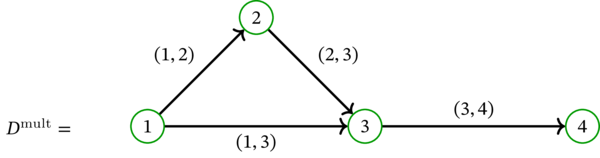
\(D=\left( V,A\right) \) を単純有向グラフとする。次の多重有向グラフを \(D\) の対応多重有向グラフ (corresponding multidigraph) と呼び、\(D^{\operatorname*{mult}}\) と表記する:
ここで \(\iota\colon A\rightarrow V\times V\) は各弧 \(a \in A\) をそれ自身に対応付ける写像である。
\(D\) を次の単純有向グラフとする:
\(D^{\operatorname*{mult}}\) は次の多重有向グラフである:
4.4.4多重有向グラフから単純有向グラフへの変換
多重有向グラフを単純有向グラフに変換する操作 \(D\mapsto D^{\operatorname*{simp}}\) も存在する:
\(D=\left( V,A,\psi\right) \) を多重有向グラフとする。次の単純有向グラフを \(D\) の台単純有向グラフ (underlying simple digraph) 呼び、\(D^{\operatorname*{simp}}\) と表記する:
言い換えれば、\(D^{\operatorname*{simp}}\) の頂点集合は \(D\) と同じ \(V\) で、\(D^{\operatorname*{simp}}\) における頂点 \(u\) から頂点 \(v\) への弧は \(G\) に \(u\) から \(v\) への弧が存在するとき、かつそのときに限って存在する1。つまり、\(D^{\operatorname*{simp}}\) は \(D\) の平行弧 (始点と終点が同じ弧) を一つに「まとめる」ことで得られる。
\(D\) を次の多重有向グラフとする:
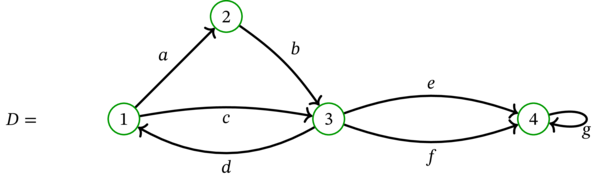
\(D^{\operatorname*{simp}}\) を次に示す:
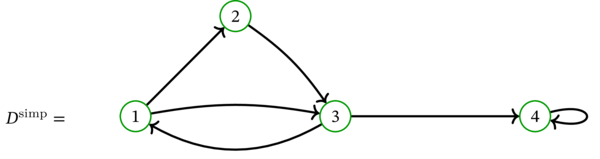
平行辺を一つに「まとめる」操作は \(c\) と \(d\) の二つの弧に影響しないことに注意してほしい。この二つの辺は始点と終点が異なるためである。同じ理由で、ループ \(g\) は保存される (無向グラフに対する同様の操作では除去されていた)。
4.4.5多重有向グラフという大きなテント
こういった変換からは、多重有向グラフがこれまでに定義した中で最も一般的なグラフの概念であることが分かる。実際、本書で定義してきた操作を使えば本書で定義した全ての種類のグラフを多重有向グラフに変換できる:
-
単純グラフは \(G\mapsto G^{\operatorname*{mult}}\) の操作で多重グラフになる。
-
そして、多重グラフは \(D\mapsto D^{\operatorname*{bidir}}\) の操作で多重有向グラフになる。
-
単純有向グラフは \(D\mapsto D^{\operatorname*{mult}}\) の操作で多重有向グラフになる。
これらの操作はどれも単射 (情報が喪失しない操作) なので、四つのグラフの概念は全て多重有向グラフにエンコードできる。このため、多重有向グラフに対する任意の定理は他の三つの種類のグラフに必ず特殊化できる。ただし、これは他の種類のグラフで成立する定理が必ず多重有向グラフに一般化できることを意味しない (例えば Mantel の定理は単純グラフでのみ成り立つ) ── そこで今後可能な場合は、多重有向グラフを使った最も一般的な形で命題を示し、議論の繰り返しを避けるようにする。
-
以前に定義しておくべきだった表現をここで定義する: \(u\), \(v\) を有向グラフの二頂点とするとき、\(u\) から \(v\) への弧 (arc from \(u\) to \(v\)) とは始点が \(u\) で終点が \(v\) の弧を意味する。 ↩︎