4.1. 有向グラフの定義

これまで本書には単純グラフと多重グラフという二つのグラフの概念が登場した。

単純グラフと多重グラフには異なる点が多いものの、共通点もある: 辺の端点が区別されない。例えば、歩道の定義では全ての辺が「両方向の」道として機能した。そのため、こういったグラフを使うと対称的な関係を上手くモデル化できる。

本章では辺が方向を持つ新しい種類の「グラフ」を二つ定義する。これらのグラフは有向グラフ (directed graph または digraph) と呼ばれる。有向グラフでは各辺が始点 (source) と終点 (target) を別々に持つ。これに対応して、有向グラフの描画では辺を矢印の付いた曲線で表し、有向グラフの頂点を動き回ることを考えるときは辺を一方向 (始点から終点に向かう方向) にしか移動できないとされる。数学的な定義は次の通りである:

定義 4.1.1

単純有向グラフ (simple digraph) とは組 \(\left( V,A\right) \) である。ここで \(V\) は有限集合を表し、\(A\) は \(V\times V\) の部分集合を表す。

定義 4.1.2

\(D=\left( V,A\right) \) を単純有向グラフとする。

\(V\) を \(D\) の頂点集合 (vertex set) と呼び、\(\operatorname*{V}\left( D\right) \) と表記する。
\(V\) の要素を \(D\) の頂点 (vertex) と呼ぶ。ノード (node) とも呼ぶ。
\(A\) を \(D\) の弧集合 (arc set) と呼び、\(\operatorname*{A}\left( D\right) \) と表記する。
\(A\) の要素を \(D\) の弧 (arc) と呼ぶ。弧は有向辺 (directed edge) とも呼ぶ。
\(V\) の要素 \(u\), \(v\) に対して、組 \(\left( u,v\right) \) を省略して \(uv\) と書く場合がある。これまでと異なり順序付きの組を表すことに注意せよ！
\(a = \left( u,v\right) \) を \(D\) の弧 (一般には \(V\times V\) の要素) とする。\(u\) を \(a\) の始点 (source) と呼び、\(v\) を \(a\) の終点 (target) と呼ぶ。
\(D\) は次のように描画する: \(D\) の各点は点で表し、各弧 \(uv\) は \(u\) を表す点から \(v\) を表す点に向かう矢印付きの曲線として表す。
\(u = v\) を満たす弧 \(\left( u,v\right) \) をループ (loop) と呼ぶ。自己ループ (self-loop) とも呼ぶ。 [言い換えれば、弧は始点が終点のとき、かつそのときに限ってループとなる。]

例 4.1.3

任意の \(n\in\mathbb{N}\) に対して、\(\left\{ 1,2,\ldots,n\right\} \) 上の整除性有向グラフ (divisibility digraph) を次の条件を満たす単純有向グラフ \(\left( V,A\right) \) と定める:

\[ \begin{aligned} V &= \left\{ 1,2,\ldots,n\right\} \\ A &= \left\{ \left( i,j\right) \in V\times V\mid i\text{ は }j \text{ を割り切る}\right\} \end{aligned} \]

例えば、\(\left\{ 1,2,\ldots,6\right\} \) 上の整除性有向グラフは次に示すグラフである:

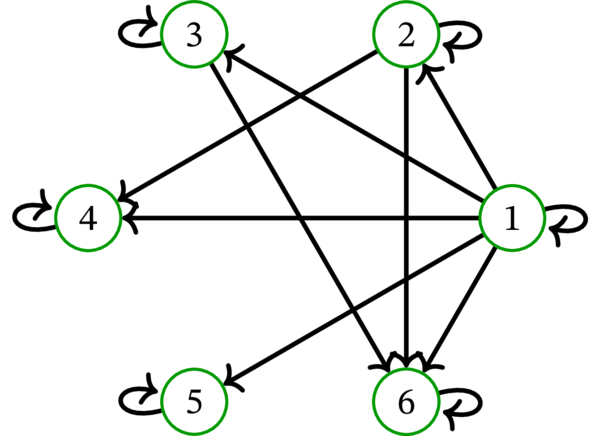
単純グラフと異なり、単純有向グラフは \(\left( v,v\right) \) の形をしたループを持てる点に注意してほしい。

定義 4.1.4

有向多重グラフ (multidigraph) とは三つ組 \(\left( V,A,\psi\right) \) である。ここで \(V\) と \(A\) は有限集合、\(\psi\colon A\rightarrow V\times V\) は写像を表す。

定義 4.1.5

\(D=\left( V,A,\psi\right) \) を多重有向グラフとする。

\(V\) を \(D\) の頂点集合 (vertex set) と呼び、\(\operatorname*{V}\left( D\right) \) と表記する。
\(V\) の要素を \(D\) の頂点 (vertex) と呼ぶ。ノード (node) とも呼ぶ。
\(A\) を \(D\) の弧集合 (arc set) と呼び、\(\operatorname*{A}\left( D\right) \) と表記する。
\(A\) の要素を \(D\) の弧 (arc) と呼ぶ。有向辺 (directed edge) とも呼ぶ。
\(a\) を \(D\) の弧とする。\(\psi\left( a\right) =\left( u,v\right) \) のとき、\(u\) を \(a\) の始点 (source) と呼び、\(v\) を \(a\) の終点 (target) と呼ぶ。
\(D\) は次のように描画する: \(D\) の各点は点で表し、各弧 \(a\) は \(u\) を表す点から \(v\) を表す点に向かう矢印付きの曲線として表す。ここで \(\left( u,v\right) =\psi\left( a\right) \) である。

例 4.1.6

有向多重グラフの例を示す:

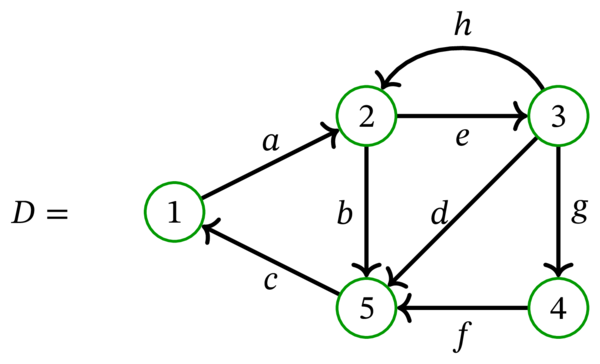
数学的に言えば、この有向多重グラフは三つ組 \(\left( V,A,\psi\right) \) である。ここで \(V=\left\{ 1,2,3,4,5\right\} \) および \(A=\left\{ a,b,c,d,e,f,g,h\right\} \) であり、\(\psi\left( a\right) =\left( 1,2\right) \), \(\psi\left( b\right) =\left( 2,5\right) \) などが成り立つ。

この定義から分かるように、単純有向グラフと多重有向グラフはそれぞれ単純グラフと多重グラフの辺を弧 (向きを持った辺) に置き換えたものと基本的に同じと言える。ただし、単純有向グラフはループを持てるのに対して単純グラフはループを持てない点は異なる (この点に関して異なる意見を持つ著者もいる)。

慣習 4.1.7

「有向グラフ」という言葉は文脈に応じて「単純有向グラフ」と「有向多重グラフ」のいずれかを意味する。

「digraph (有向グラフ)」という単語は元々「directed graph (向きを持ったグラフ)」の短縮形だったものの、現在では上述した意味を持つ専門用語であり、グラフ理論を学んだ人なら誰でも理解できる (言語学では digraph が異なる意味で使われる)。