4.9. グラフの反転と補グラフ

ハミルトン (閉) 路からは一度離れて、単純有向グラフに対する新しい操作を二つ定義する。

定義 4.9.1

\(D=\left( V,A\right) \) を単純有向グラフとする。このとき:

\(\left( V\times V\right) \setminus A\) の要素を \(D\) の非弧 (non-arc) と呼ぶ。
組 \(\left( i,j\right) \in V\times V\) の反転 (reversal) とは組 \(\left( j,i\right) \) を意味する。
\(D^{\operatorname*{rev}}\) を単純有向グラフ \(\left( V,A^{\operatorname*{rev}}\right) \) と定義する。ここで \(A^{\operatorname*{rev}}\) は次のように定義される:

\[ A^{\operatorname*{rev}}=\left\{ \left( j,i\right) \mid \left( i,j\right) \in A\right\} \]

つまり、\(D\) の弧を反転させて (始点と終点を入れ替えることで) 得られる単純有向グラフが \(D^{\operatorname*{rev}}\) である。\(D^{\operatorname*{rev}}\) を \(D\) の反転 (reversal) と呼ぶ。
\(\overline{D}\) を単純有向グラフ \(\left( V,\ \ \left( V\times V\right) \setminus A\right) \) と定義する。\(\overline{D}\) の頂点は \(D\) と同じであり、弧は \(D\) の非弧とちょうど等しい。この単純有向グラフ \(\overline{D}\) を \(D\) の補グラフ (complement) と呼ぶ。

例 4.9.2

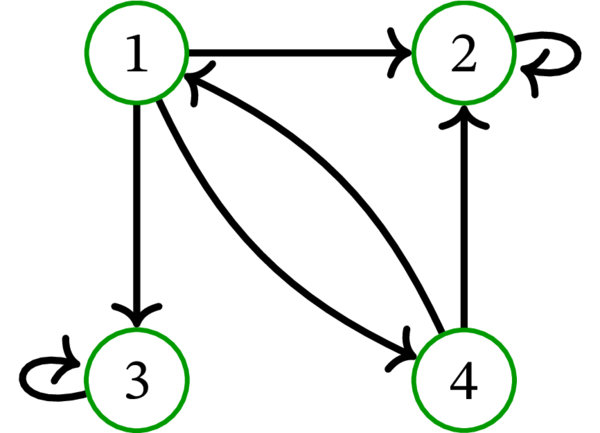
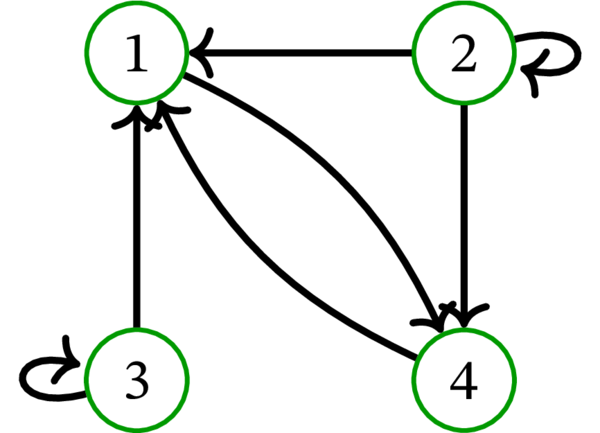
次の単純有向グラフを \(D\) とする:

\(D\) =

このとき \(D^{\operatorname*{rev}}\) と \(\overline{D}\) は次の単純有向グラフとなる:

\(D^{\operatorname*{rev}}\) =

\(\overline{D}\) =

慣習 4.9.3

以降の議論では、記号 \(\text{\# }\) で「...の個数」を表す。例えば、次の等式が成り立つ:

\[ \left( \text{\# } \left\{ 1,2,3\right\} \text{ の部分集合} \right) =8 \]

これから単純有向グラフが持つハミルトン路の個数について議論する¹。まずは準備運動として、次の簡単な命題を示す:

命題 4.9.4

次の \(V\), \(A\) を使って定義される単純有向グラフ \(\left( V,A\right) \) を \(D\) とする:

\[ \begin{aligned} V &= \left\{ 1,2,\ldots,n\right\} \qquad \left(n\in\mathbb{N}\right) \\ A &= \left\{ \left( i,j\right) \mid i < j\right\} \end{aligned} \]

このとき \(\left( \text{\# } D \text{ のハミルトン路} \right) = 1\) が成り立つ。

[証明] \(D\) の唯一のハミルトン路が \(\left( 1,2,\ldots,n\right) \) であることは容易に分かる。□

次の命題も簡単に示せる:

命題 4.9.5

\(D\) を単純有向グラフとする。このとき、次の等式が成り立つ:

\[ \left(\text{\# } D^{\operatorname*{rev}} \text{ のハミルトン路}\right) = \left(\text{\# } D \text{ のハミルトン路}\right) \]

[証明] \(D\) のハミルトン路を逆走すれば \(D^{\operatorname*{rev}}\) のハミルトン路が得られる。逆も同様に言える。□

あまり面白く命題が続いた。次の定理はどうだろう:

定理 4.9.6

[Berge の定理 (Berge's theorem)] \(D\) を単純有向グラフとする。このとき、次の等式が成り立つ:

\[ \left(\text{\# } \overline{D} \text{ のハミルトン路}\right) \equiv \left(\text{\# } D \text{ のハミルトン路}\right) \ \bmod 2 \]

これは今までの命題と比べて自明でないし、予想される結果でもない。まず例を示す:

例 4.9.7

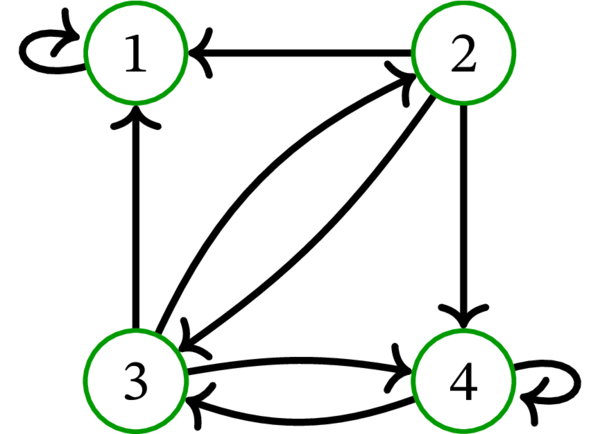
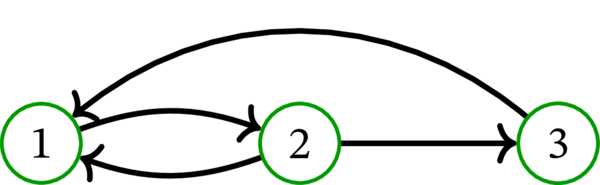
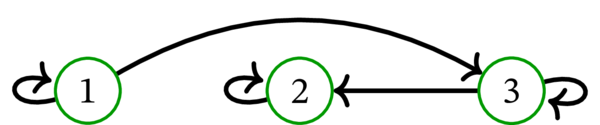
\(D\) を次の単純有向グラフとする:

\(D\) =

\(D\) は \(3\) 個のハミルトン路を持つ: \(\left( 1,2,3\right) \) と \(\left( 2,3,1\right) \) と \(\left( 3,1,2\right) \) である。

\(D\) の補グラフ \(\overline{D}\) を示す:

\(\overline{D}\) =

\(\overline{D}\) はハミルトン路を \(1\) 個しか持たない: \(\left( 1,3,2\right) \) である。

このとき、定理 4.9.6 が主張する \(1\equiv 3 \bmod 2\) は確かに成り立つ。

[定理 4.9.6 の証明] [ここには証明の概略を示す。詳細は [17s-lec7, proof of Theorem 1.3.6] を参照してほしい。]

単純有向グラフ \(D\) を \(D=\left( V,A\right) \) と書く。また、一般性を失うことなく \(V \neq \varnothing\) と仮定する。\(n=\left\vert V\right\vert \) と定める。

\(V\) の各要素をちょうど一度ずつ含む \(V\) の要素の列を \(V\)-列挙 (\(V\)-listing) と呼ぶ。 [つまり \(V\) 列挙は長さ \(n\) の列であり、全部で \(n!\) 個の \(V\) 列挙が存在する。] 例えば、任意の \(V\) 列挙は完全な単純有向グラフ \(\left( V,V\times V\right) \) のハミルトン路に等しい。また、\(D\) または \(\overline{D}\) のハミルトン路は \(V\) 列挙であるものの、全ての \(V\) 列挙が \(D\) または \(\overline{D}\) のハミルトン路であるわけではない。

\(V\) 列挙 \(\sigma=\left( \sigma_{1},\sigma_{2},\ldots,\sigma_{n}\right) \) に対して、集合 \(P\left( \sigma\right)\) を次のように定める:

\[ P\left( \sigma\right) \colonequals \left\{ \sigma_{1}\sigma_{2},\ \sigma_{2}\sigma _{3},\ \ldots,\ \sigma_{n-1}\sigma_{n}\right\} \]

集合 \(P\left( \sigma\right)\) を \(\sigma\) の弧集合 (arc set) と呼ぶ。\(\sigma\) を単純有向グラフ \(\left( V,V\times V\right) \) のハミルトン路とみなすとき、\(P\left( \sigma\right) \) は \(\sigma\) に含まれる弧全体を表す集合となる。\(P\left( \sigma\right) \) の要素数が \(n-1\) であることに注意する。次の観察は簡単に確かめられる: [証明せよ！]

観察 1: 弧集合 \(P\left( \sigma\right) \) から \(V\) 列挙 \(\sigma\) を一意に構築できる。つまり、写像 \(\sigma\mapsto P\left( \sigma\right) \) は単射である。

観察 2: \(V\) 列挙 \(\sigma\) は \(P\left( \sigma\right) \subseteq A\) を満たすとき、かつそのときに限って \(D\) のハミルトン路となる。

観察 3: \(V\) 列挙 \(\sigma\) は \(P\left( \sigma\right) \subseteq \left( V\times V\right) \setminus A\) を満たすとき、かつそのときに限って \(\overline{D}\) のハミルトン路となる。

\(N\) を組 \(\left( \sigma,B\right) \) の総数とする。ここで \(\sigma\) は \(V\) 列挙を表し、\(B\) は \(B\subseteq P\left( \sigma\right) \) を満たす \(A\) の部分集合を表す。このとき、次の等式が成り立つ:

\[ \begin{aligned} N = & \sum_{\sigma:\ V \text{列挙}}N_{\sigma} \\ N_{\sigma} \colonequals &\left(\text{\# } B\subseteq P\left( \sigma\right) \text{ を満たす } A \text{ の部分集合 } B \right) \end{aligned} \]

一方、次の等式も成り立つ:

\[ \begin{aligned} N = &\sum_{B \subseteq A}N^{B} \\ N^{B} \colonequals & \left( \text{\# } B\subseteq P\left( \sigma\right) \text{ を満たす } V \text{ 列挙 } \sigma \right) \end{aligned} \]

これら二つの和をハミルトン路と関連付けよう。まず \(\sum\limits_{\sigma:\ V \text{ 列挙}}N_{\sigma}\) から始める。

以降の議論では Iverson の括弧記法 (Iverson bracket notation) を用いる。つまり、命題 \(\mathcal{A}\) の真偽値を表す \(1\) または \(0\) を \(\left[ \mathcal{A}\right] \) と表記する。\(\mathcal{A}\) が真のとき \(\left[ \mathcal{A}\right] \) は \(1\) となり、\(\mathcal{A}\) が偽のとき \(\left[ \mathcal{A}\right] \) は \(0\) となる。例えば、次の等式が成り立つ:

\[ \begin{aligned} \left[ 2+2=4\right] &= 1\\ \left[ 2+2=5\right] &= 0 \end{aligned} \]

任意の \(V\) 列挙 \(\sigma\) に対して、\(N_{\sigma}\) は次のように変形できる:

\[ \begin{aligned} N_{\sigma} & =\left(\text{\# } B\subseteq P\left( \sigma\right) \text{ を満たす } A \text{ の部分集合 } B \right) \\ & =\left(\text{\# } A\cap P\left( \sigma\right) \text{ の部分集合 } B \right) \\ & =2^{\left\vert A\cap P\left( \sigma\right) \right\vert }\\ & \equiv\left[ \left\vert A\cap P\left( \sigma\right) \right\vert =0\right] \bmod 2 \\ & \qquad \left(\because\ \text{任意の } m\in\mathbb{N} \text{ に対して } 2^{m}\equiv\left[ m=0\right] \bmod 2 \right) \\ & \equiv \left[ A\cap P\left( \sigma\right) =\varnothing\right] \bmod 2\\ & \qquad \left( \because\ \text{括弧内の命題の真偽が一致する} \right) \\ & \equiv\left[ P\left( \sigma\right) \subseteq\left( V\times V\right) \setminus A\right] \bmod 2 \\ & \qquad \left(\because\ P\left( \sigma\right) \text{ は必ず } V\times V \text{ の部分集合}\right) \\ & \equiv\left[ \sigma\text{ は }\overline{D} \text{ のハミルトン路}\right] \bmod 2 \\ & \qquad \left(\because\ \text{観察 3}\right) \end{aligned} \]

よって次を得る:

\[ \begin{aligned} N & =\sum_{\sigma:\ V \text{ 列挙}} N_{\sigma} \\ & \equiv \left( \sum_{\sigma:\ V \text{ 列挙}}\left[ \sigma \text{ は }\overline{D} \text{ のハミルトン路}\right] \right) \bmod 2 \\ & \equiv \left(\text{\# } \overline{D} \text{ のハミルトン路である } V \text{ 列挙 } \sigma \right) \bmod 2 \\[5pt] & \qquad \left(\begin{aligned} \because\ &\left[ \sigma \text{ は }\overline{D} \text{ のハミルトン路}\right] \text{ は } 0 \text{ または } 1 \text{ であり、 } 1 \text{ の場合に} \\ &\ \text{一対一に対応して } \overline{D} \text{ のハミルトン路である } V \text{ 列挙 } \sigma \text{ が存在する}\end{aligned} \right) \\[15pt] & \equiv \left(\text{\# } \overline{D} \text{ のハミルトン路} \right) \bmod 2 \end{aligned} \]

もう一つの \(N\) の表現についてはどうだろうか？思い出しておくと、次の関係が得られていた:

\[ \begin{aligned} N &= \sum_{B \subseteq A}N^{B} \\ N^{B} &= \left( \text{\# } B\subseteq P\left( \sigma\right) \text{ を満たす } V \text{ 列挙 } \sigma \right) \end{aligned} \]

この関係を使って、\(\left(\text{\# } D \text{ のハミルトン路} \right)\) が \(2\) を法として \(N\) と合同なことを証明したい。

\(B\) を \(A\) の部分集合とする。知りたいのは \(N^{B} \bmod 2\) の値である。言い換えれば、\(N^{B}\) が奇数となる条件を知りたい。

まずは \(N^{B}\) が奇数と仮定して、そこから何が導けるかを考えてみよう。

\(N^{B}\) が奇数なので、\(N^{B} > 0\) が成り立つ。よって \(B\subseteq P\left( \sigma\right) \) を満たす \(V\) 列挙 \(\sigma\) が少なくとも一つ存在する。ここからはいくつかの結果を導ける。

まず用語を定義する: \(V\) の路被覆 (path cover) とは、完全な有向グラフ \(\left( V,V\times V\right) \) の路からなる集合であって、各頂点 \(v\in V\) がいずれかの路にちょうど一度ずつ含まれるものを言う。路被覆の弧集合とは、路被覆に含まれる路の弧を全て集めた集合を言う。例えば \(V=\left\{ 1,2,3,4,5,6,7\right\} \) なら、次の集合は \(V\) の路被覆である:

\[ \left\{ \left( 1,3,5\right) ,\ \ \left( 2\right) ,\ \ \left( 6\right) ,\ \ \left( 7,4\right) \right\} \]

また、この路被覆の弧集合は \(\left\{ 13,\ 35,\ 74\right\} \) である。

続いて、次の事実に注目する: 路 \(\left( v_{1},v_{2},\ldots,v_{k}\right) \) から弧 \(v_{i}v_{i+1}\) を取り除くと、二つの路 \(\left( v_{1},v_{2},\ldots,v_{i}\right) \) と \(\left( v_{i+1},v_{i+2},\ldots,v_{k}\right) \) が得られる。そのため \(V\) 列挙 \(\sigma\) の弧集合 \(P\left( \sigma\right) \) から弧をいくつか取り除くと、何らかの \(V\) の路被覆に対応する路集合が得られる。 [例えば \(V\) 列挙 \(\sigma=\left( 1,3,5,2,6,7,4\right) \) の弧集合 \(P\left( \sigma\right) \) から弧 \(52\), \(26\), \(67\) を取り除くと弧の集合 \(\left\{ 13,\ 35,\ 74\right\} \) が得られる。これは先ほど例として出した路被覆 \(\left\{ \left( 1,3,5\right) ,\ \ \left( 2\right) ,\ \ \left( 6\right) ,\ \ \left( 7,4\right) \right\} \) の弧集合である。]

\(B\subseteq P\left( \sigma\right) \) を満たす \(V\) 列挙 \(\sigma\) が少なくとも一つ存在すると先ほど仮定したのだった。このとき \(B\) は \(V\) 列挙 \(\sigma\) の弧集合 \(P\left( \sigma\right) \) から弧をいくつか取り除くことで得られるので、前段落の議論より、弧集合が \(B\) である \(V\) の路被覆が存在する。この路被覆に含まれる路の個数を \(r\) とすれば、次の等式が成り立つ:

\[ \left(\text{\# } B \subseteq P\left( \sigma\right) \text{ を満たす } V \text{ 列挙 } \sigma \right) =r! \]

なぜなら、\(B \subseteq P\left( \sigma\right)\) を満たす \(V\) 列挙 \(\sigma\) は弧集合が \(B\) である \(V\) の路被覆に含まれる \(r\) 個の路を並べ替えることで得られるからである (\(r\) 個の路の並べ方は \(r!\) 通りある)。

よって \(N^{B} =\left( \text{\# } B \subseteq P\left( \sigma\right) \text{ を満たす } V \text{ 列挙 } \sigma\right) = r! \) を得る。\(N^{B}\) は奇数という仮定より \(r!\) は奇数である。\(V \neq \varnothing\) より \(r\) は正 (\(V\) の路被覆には路が少なくとも一つ含まれる) と分かり、最終的に \(r=1\) と結論できる。つまり、先ほど考えていた \(V\) の路被覆には路が一つしか含まれない。この路は (\(B \subseteq A\) より) \(D\) の路であり、従って (自身だけで \(V\) の路被覆となることから) \(D\) のハミルトン路である。この路を \(\sigma\) とすれば、\(\sigma\) だけからなる路被覆の弧集合が \(B\) なので、\(B=P\left( \sigma\right) \) が成り立つ。

以降の議論では \(N^{B}\) が奇数という仮定を忘れる。ここまでの議論で示されたのは「\(N^B\) が奇数なら、\(B=P\left( \sigma\right) \) となる \(D\) のハミルトン路 \(\sigma\) が存在する」である。

これと逆の命題「\(B=P\left( \sigma\right) \) となる \(D\) のハミルトン路 \(\sigma\) が存在するなら、\(N^{B}\) は奇数 (実際には \(N^{B} = 1\))」は簡単に示せる。

この二つの結果を組み合わせると「\(N^{B}\) が奇数」と「\(B=P\left( \sigma\right) \) となる \(D\) のハミルトン路 \(\sigma\) が存在する」が同値であると分かる。ここから次の等式を得る:

\[ \left[ N^{B}\text{ が奇数}\right] =\left[ B=P\left( \sigma\right) \text{ となる } D \text{ のハミルトン路 } \sigma \text{ が存在する} \right] \]

これを使えば \(N^{B}\) を次のように変形できる:

\[ \begin{aligned} N^{B} & \equiv\left[ N^{B}\text{ が奇数}\right] \bmod 2 \\ & \qquad \left( \because\ \text{任意の } m\in\mathbb{Z} \text{ で } m\equiv\left[ m\text{ が奇数}\right] \bmod 2 \right) \\ & \equiv \left[ B=P\left( \sigma\right) \text{ となる } D \text{ のハミルトン路 } \sigma \text{ が存在する} \right] \bmod 2 \end{aligned} \]

この合同関係は \(A\) の任意の部分集合 \(B\) に対して成り立つので、\(N\) は次のように書き換えられる:

\[ \begin{aligned} N & =\sum_{B \subseteq A} N^{B} \\[4pt] & \equiv \left(\sum_{B \subseteq A}\left[ B=P\left( \sigma\right) \text{ となる } D \text{ のハミルトン路 } \sigma \text{ が存在する} \right]\right) \bmod 2 \\[4pt] & \equiv \left(\begin{aligned}\text{\# } &B=P\left( \sigma\right) \text{ となる } D \text{ のハミルトン路 } \sigma \text{ が存在するような} \\[4pt] & A \text{ の部分集合 } B\end{aligned} \right) \bmod 2 \\[4pt] & \equiv \left(\text{\# } D \text{ のハミルトン路 } \sigma \text{ を使って } P\left(\sigma\right) \text{ と書ける集合} \right) \bmod 2 \\ & \qquad \left( \because\ \text{観察 2 より } D \text{ のハミルトン路 } \sigma \text{ に対する } P\left(\sigma\right) \text{ は } A \text{ の部分集合} \right) \\[4pt] & \equiv \left( \text{\# } D \text{ のハミルトン路}\right) \bmod 2 \end{aligned} \]

[最後の式変形について: 観察 1 から、異なるハミルトン路 \(\sigma\) からは異なる \(P\left( \sigma\right) \) が得られると分かる。よって全てのハミルトン路 \(\sigma\) に対する \(P\left( \sigma\right) \) の個数を数えることは、ハミルトン路 \(\sigma\) の個数そのものを数えることに等しい。]

よって \(N\equiv\left(\text{\# } \overline {D} \text{ のハミルトン路}\right) \bmod 2\) と \(N\equiv\left(\text{\# } D \text{ のハミルトン路} \right) \bmod 2\) が証明できた。ここから次の合同関係を得る:

\[ \left(\text{\# } \overline{D} \text{ のハミルトン路}\right) \equiv \left(\text{\# } D \text{ のハミルトン路} \right) \bmod 2 \]

以上で Berge の定理は証明された。□

この話題に関する詳細な解説については [17s-lec7] を参照してほしい。 ↩︎