4.10. トーナメント
4.10.1 定義
続いて、特別な種類の単純有向グラフを定義する。
有向グラフ \(D\) がループを持たないとき、\(D\) はループレス (loopless) と言う。
ループレスな単純有向グラフ \(D\) が次の条件を満たすとき、\(D\) をトーナメント (tournament) と呼ぶ:
-
トーナメント公理: \(D\) の任意の異なる二頂点 \(u\), \(v\) に対して、\(\left( u,v\right) \) と \(\left( v,u\right) \) のちょうど一方のみが \(D\) の弧である。
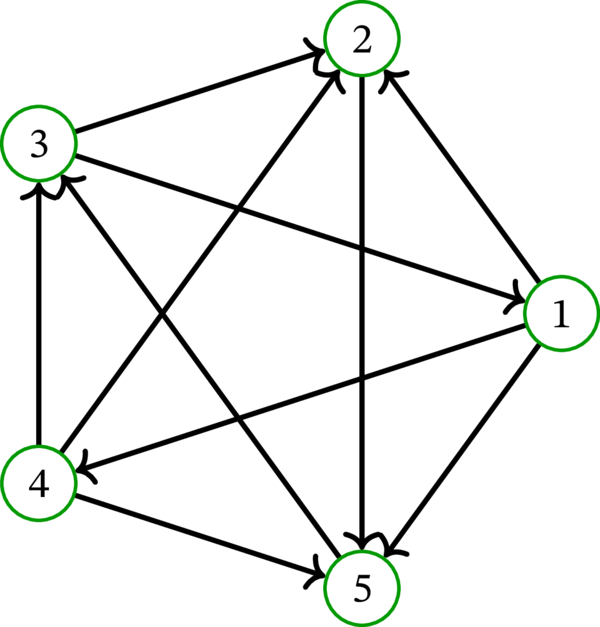
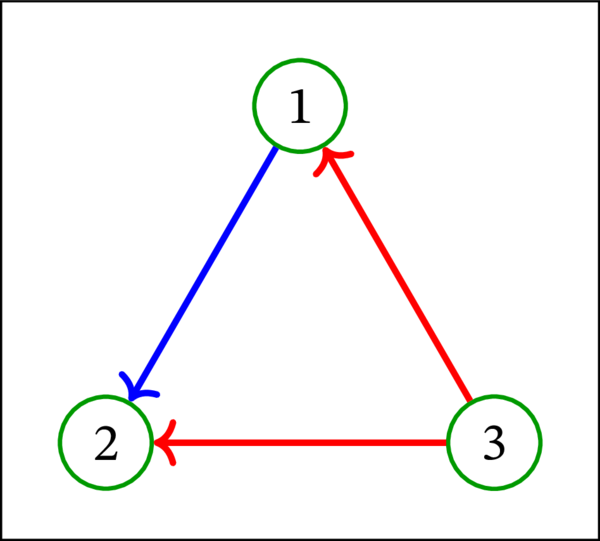
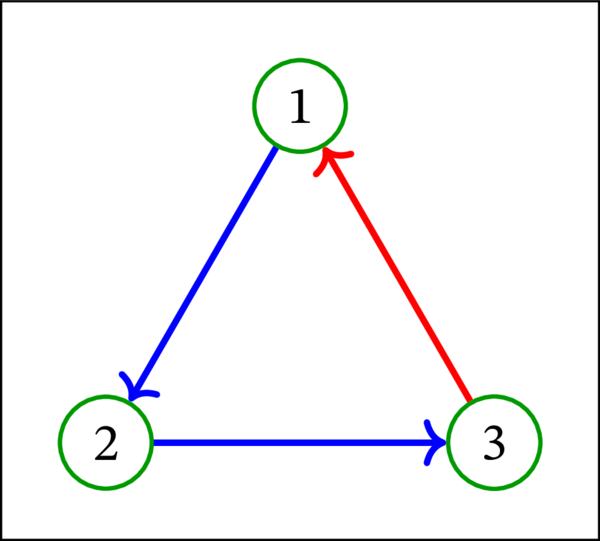
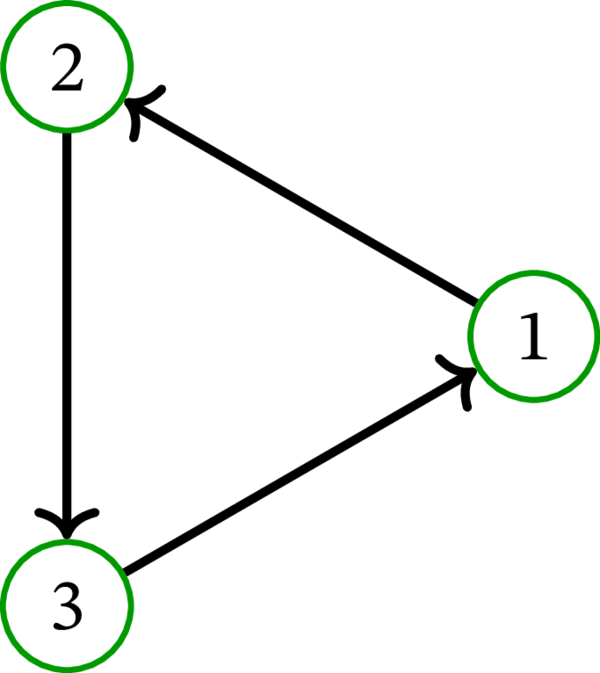
次の有向グラフはトーナメントである:
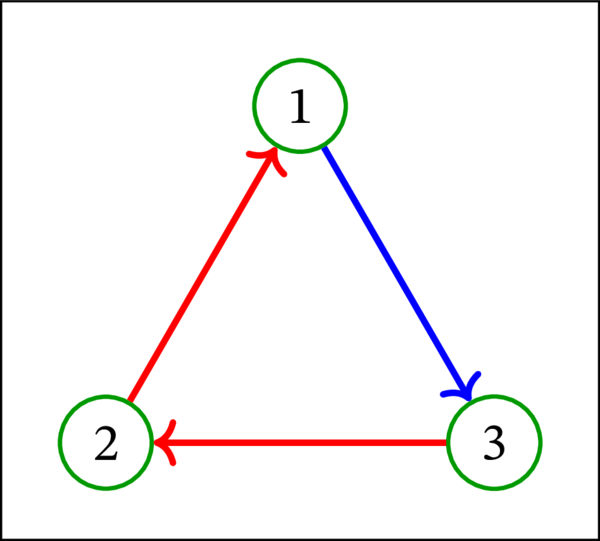
次の有向グラフもトーナメントである:
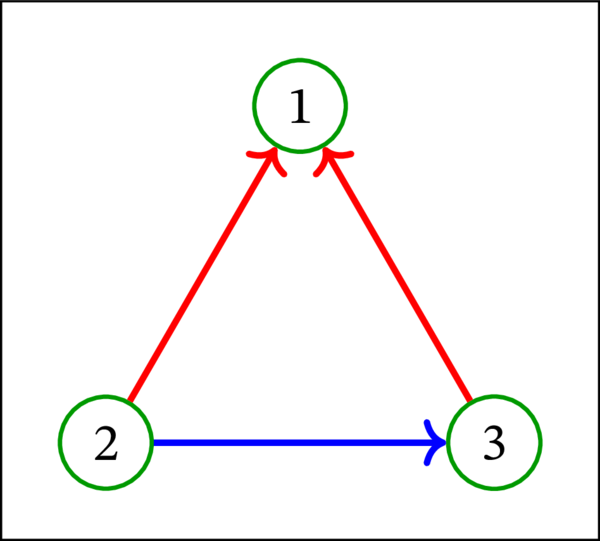
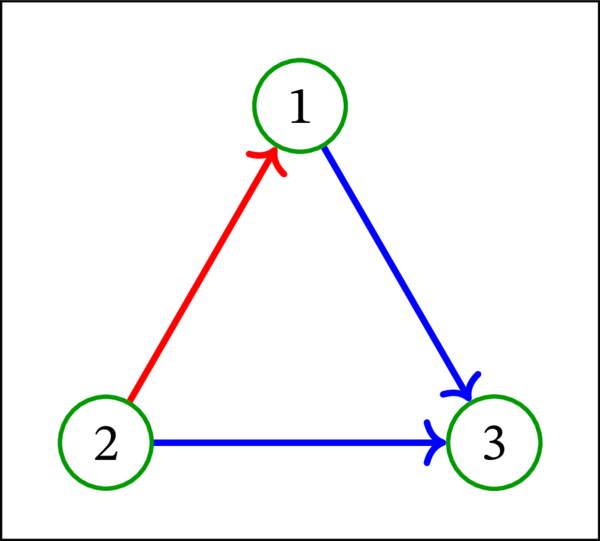
一方で、次の有向グラフはトーナメントでない:
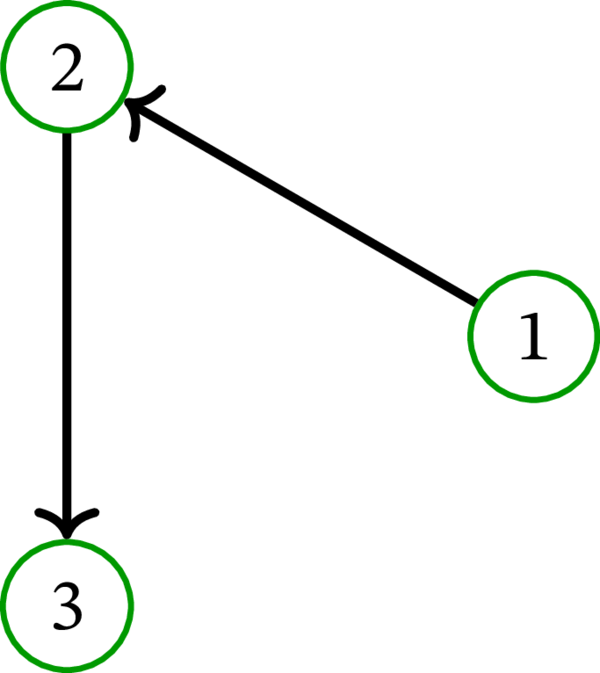
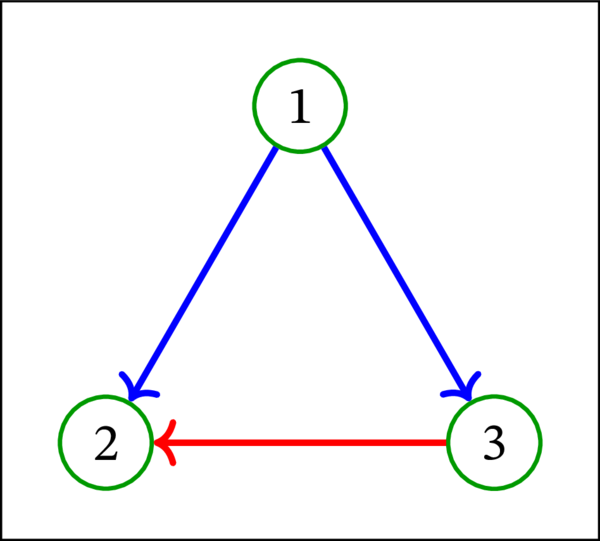
このグラフでは \(u=1\), \(v = 2\) に対してトーナメント公理が満たされない。同様に次の有向グラフもトーナメントでない:
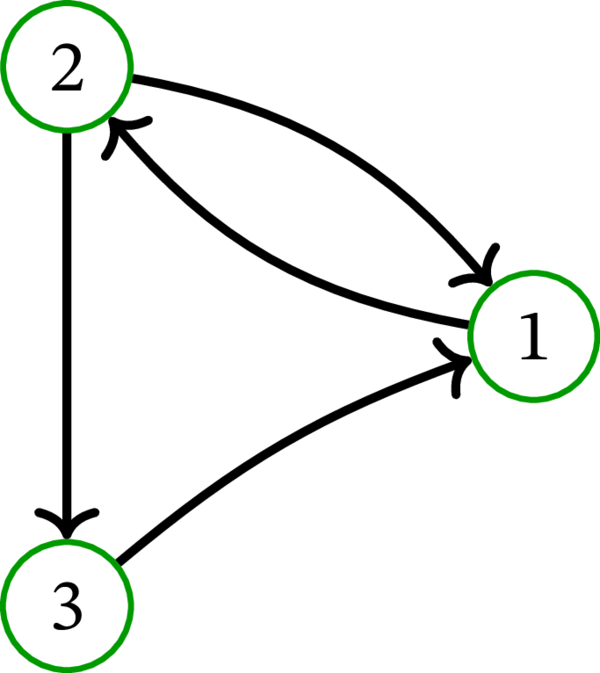
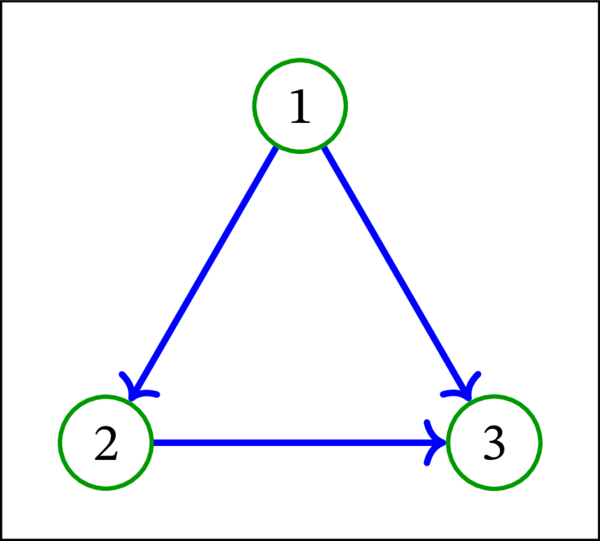
次の有向グラフはループレスでないので、トーナメントでもない:
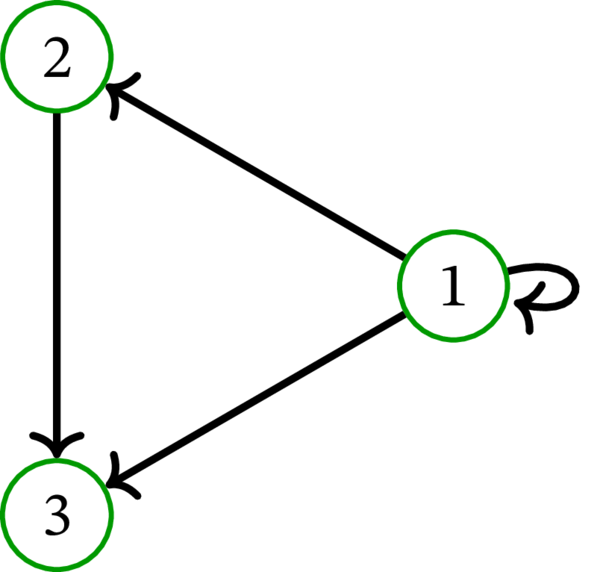
命題 4.9.4 で示した有向グラフ \(D\) は必ずトーナメントである。
トーナメントは「任意に向き付けされた完全グラフ」と解釈することもできる。
定義 4.9.1 を使うと、トーナメントの定義は次のように言い換えられる:
\(D=\left( V,A\right) \) をループレスな単純有向グラフとする。このとき、\(\overline{D}\) のループでない弧の集合が \(D^{\operatorname*{rev}}\) の弧集合に等しいとき、かつそのときに限って \(D\) はトーナメントとなる。
定義から容易に分かる。□
少なくとも一つの頂点を持つトーナメントを \(D\) とする。
\(D\) の頂点 \(u\) が \(D\) の頂点 \(w\) に直接的に勝利する (directly own) とは、\(\left( u,w\right) \) が \(D\) の弧であることを言う。
\(D\) の頂点 \(u\) が \(D\) の頂点 \(w\) に間接的に勝利する (indirectly own) とは、\(\left( u,v\right) \) と \(\left( v,w\right) \) の両方が \(D\) の弧であるような \(D\) の頂点 \(v\) が存在することを言う。
他の全ての頂点に (直接的または間接的に) 勝利する \(D\) の頂点が存在することを示せ。
4.10.2 Rédei の定理
どんなトーナメントがハミルトン路を持つだろうか? 答えは意外なほどに単純である1:
任意のトーナメントは少なくとも一つのハミルトン路を持つ。
さらに優れた、そしておそらくはさらに意外な結果も知られている:
任意のトーナメントが持つハミルトン路の個数は奇数である。
この二つの定理をこれから証明する。明らかに、弱い Rédei の定理は強い Rédei の定理から従う (\(0\) は奇数でないため)。よって強い Rédei の定理を示せばよい。
Rédei の定理の証明では、次の重要な補題が利用される:
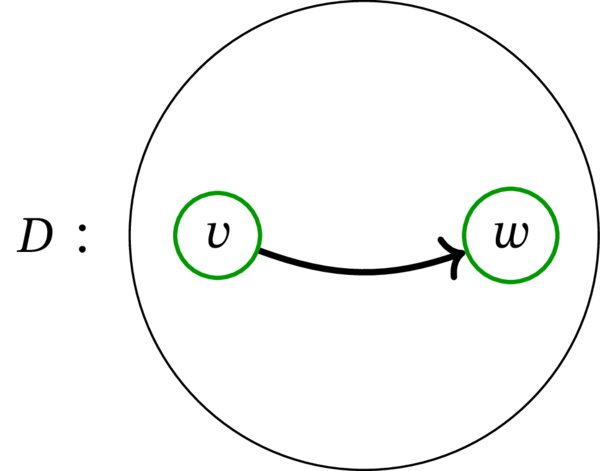
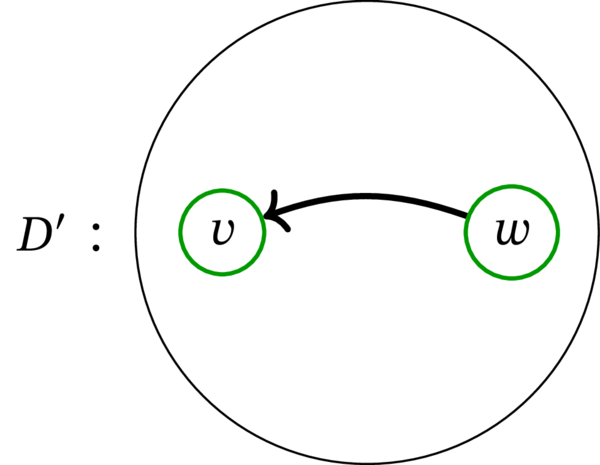
\(D=\left( V,A\right) \) をトーナメント、\(vw \in A\) を \(D\) の弧とする。
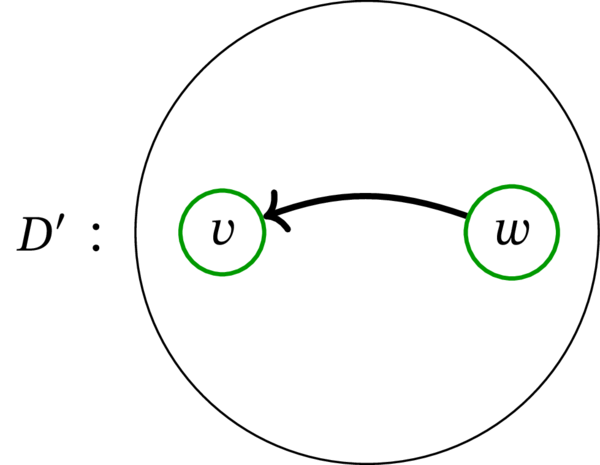
\(D\) の弧 \(vw\) を反転させて得られるグラフを \(D^{\prime}\) とする。言い換えれば、\(D^{\prime}\) を次のように定める:
このとき \(D^{\prime}\) はトーナメントであり、次の等式が成り立つ:
補題 4.10.8 の設定を表す図を示す:
ここには \(v\) と \(w\) を接続する弧しか描かれていない。他の弧は共通である。
まず、\(D^{\prime}\) がトーナメントなことは容易に分かる。これから合同関係を示す。
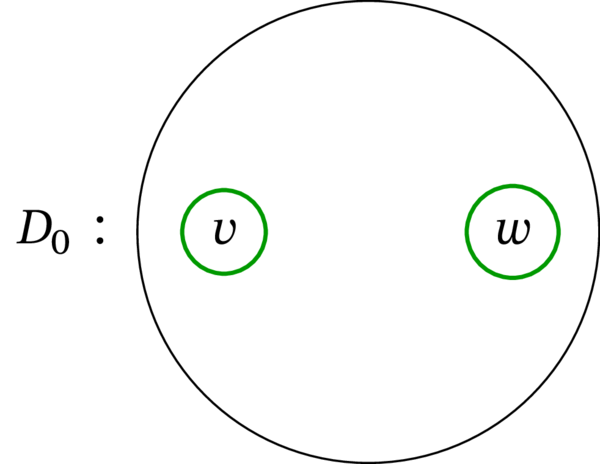
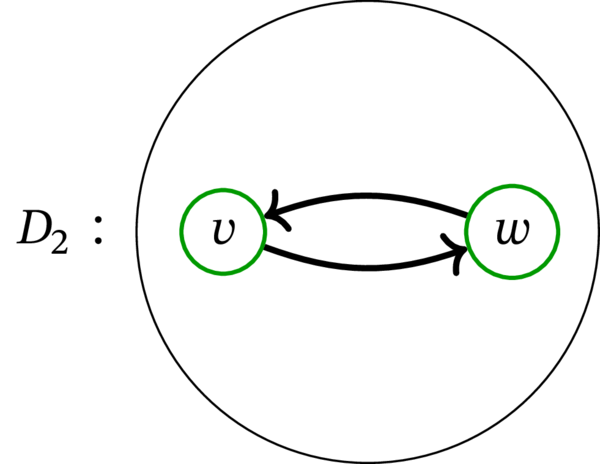
\(D\), \(D^{\prime}\) とは別に二つの有向グラフを定義する:
\(D_{0}\) と \(D_{2}\) はトーナメントでないことに注意する。\(D\), \(D^{\prime}\), \(D_{0}\), \(D_{2}\) を表す図を次に示す。ここでも \(v\) と \(w\) を接続する (変化のある) 弧だけを示している:
\(D_{0}\) は \(D^{\prime}\) から弧 \(wv\) を取り除いた有向グラフである。よって \(D_{0}\) のハミルトン路は弧 \(wv\) を使わない \(D^{\prime}\) のハミルトン路に等しい。従って次の等式が成り立つ:
同様に、\(D\) は \(D_{2}\) から弧 \(wv\) を取り除いた有向グラフだから、次の等式が成り立つ:
先ほど示した等式
からは、次の合同関係が得られる:
よって、次の合同関係が示せれば補題の証明が完了する:
なぜなら、次のように変形できるからである:
よって \(\left(\text{\# } D_{2} \text{ のハミルトン路}\right) \equiv \left(\text{\# } D_{0} \text{ のハミルトン路}\right) \bmod 2 \) を示せばよい。\(D\) はトーナメントなので、\(\overline{D}\) のループでない弧の集合は \(D^{\operatorname*{rev}}\) の弧集合に等しい (命題 4.10.5)。よって \(\overline{D_{0}}\) のループでない弧の集合は \(D_{2}^{\operatorname*{rev}}\) の弧集合に等しい (\(\overline{D_{0}}\) は \(\overline{D}\) に弧 \(vw\) を加えたものであり、\(D_{2}^{\operatorname*{rev}}\) は \(D^{\operatorname*{rev}}\) に弧 \(vw\) を加えたものであるため)。従って、有向グラフ \(\overline{D_{0}}\) と \(D_{2}^{\operatorname*{rev}}\) は「ループを除いて」等しい (同じ頂点を持ち、ループ以外の弧が等しい)。ハミルトン路を考えるときループは存在しないとみなせるので、この二つの有向グラフは同じ個数のハミルトン路を持つ。よって命題 4.9.5 より次の等式を得る:
これと定理 4.9.6 から次の合同関係を得る:
先述したように、これで補題 4.10.8 の証明が完了した。□
この補題があれば、強い Rédei の定理は簡単に証明できる:
\(D\) のハミルトン路の個数が奇数だと示す必要がある。補題 4.10.8 より、トーナメント \(D\) が持つハミルトン路の個数の偶奇は \(D\) の弧を一つ反転させたとしても変わらないと分かる。よって \(D\) の弧をいくつ反転させたとしても \(D\) が持つハミルトン路の個数の偶奇は変わらない。\(D\) の頂点が \(1,2,\ldots,n\) (\(n \in \mathbb{N}\)) だと一般性を失うことなく仮定する。このとき \(D\) の弧を適切に反転させることで、次の弧を持つトーナメントが得られる:
このトーナメントのハミルトン路は \(\left( 1,2,\ldots,n\right) \) の一つしか存在しない。トーナメントの弧を反転させてもハミルトン路の個数の偶奇は変化しないので、元の \(D\) も奇数個のハミルトン路を持つと結論できる。以上で強い Rédei の定理 (定理 4.10.7) は証明された。□
先述の通り、弱い Rédei の定理は強い Rédei の定理から従う。ただ、弱い Rédei の定理を直接示す短い証明 [17s-lec7, Theorem 1.4.9] も存在する。
定理 4.10.7 からは、トーナメントが持つハミルトン路の個数が正の奇数だと分かる。では、その個数は任意の正の奇数となれるのだろうか? それとも、トーナメントが持つハミルトン路の個数になり得ない正の奇数が存在するだろうか?
意外なことに、\(7\) 個あるいは \(21\) 個のハミルトン路を持つトーナメントは存在しないことが示されている。これらを除くと、\(1\) から \(80555\) までの全ての奇数はトーナメントの持つハミルトン路の個数として可能なことが確かめられている。これより大きい数値に対する答えは分かっていない。MathOverflow の question #232751 [MO232751] に詳細がある。
4.10.3 ハミルトン閉路とトーナメント
弱い Rédei の定理によると、任意のトーナメントはハミルトン路を持つ。しかし当然、任意のトーナメントがハミルトン閉路を持つわけではない。次の条件は明らかである:
有向グラフ \(D\) がハミルトン閉路を持つなら、\(D\) は強連結である。
一般に、この条件はハミルトン閉路を持つことの必要条件であり、十分条件ではない。強連結な有向グラフが必ずハミルトン閉路を持つわけではない。しかし、\(2\) 個以上の頂点を持つトーナメントに対しては十分条件にもなる:
トーナメント \(D\) が \(2\) 個以上の頂点を持ち強連結なら、\(D\) はハミルトン閉路を持つ。
詳細な証明は [17s-lec7, Theorem 1.5.5] にある。ここには非常に粗い概略を示す。
\(D=\left( V,A\right) \) を \(2\) 個以上の頂点を持つ強連結なトーナメントとする2。\(D\) がハミルトン閉路を持つことを示す必要がある。
\(D\) が閉路を持つことは容易に分かる。\(\mathbf{c}=\left( v_{1},v_{2},\ldots,v_{k},v_{1}\right) \) を長さが最大の閉路として、\(\mathbf{c}\) がハミルトン閉路であることをこれから示す。
この閉路 \(\mathbf{c}\) の頂点を \(C = \left\{ v_{1},v_{2},\ldots,v_{k}\right\} \) とする。
頂点 \(w\in V\setminus C\) が終頂点 (to-vertex) とは、いずれかの \(v_{i}\) から \(w\) への弧が存在することを言う。
頂点 \(w\in V\setminus C\) が始頂点 (from-vertex) とは、\(w\) からいずれかの \(v_{i}\) への弧が存在することを言う。
\(D\) はトーナメントなので、\(V \setminus C\) の各頂点は終頂点または始頂点となる。理論上は終頂点かつ始頂点の頂点 (いずれかの \(v_{i}\) から自身への弧と、自身からいずれかの \(v_{j}\) への弧を両方持つ頂点) も存在できるものの、この頂点は実際には存在しない。これは次の議論から分かる:
-
終頂点 \(w\) が \(v_{i}\) からの弧を持つなら、\(v_{i+1}\)3 から \(w\) への弧も存在しなければならない (そうでなければ \(D\) はトーナメントより \(w\) から \(v_{i+1}\) への弧が存在するものの、このとき \(\mathbf{c}\) の \(v_{i}\) と \(v_{i+1}\) の間に \(w\) を入れることで \(\mathbf{c}\) を長くできてしまう。これは \(\mathbf{c}\) が長さ最大の閉路である仮定と矛盾する)。
-
この議論を繰り返せば、終頂点 \(w\) が \(v_{i}\) からの弧を持つとき \(v_{i+1}\), \(v_{i+2}\), ... からの弧も持つと分かる。つまり \(w\) は \(\mathbf{c}\) の全ての頂点からの弧を持つ。よって \(w\) は終頂点になれない。以上で「終頂点は始頂点でない」が証明された。
\(F\) を始頂点全体の集合、\(T\) を終頂点全体の集合とする。このとき、先ほど示したように \(F\) と \(T\) は共通要素を持たない。さらに \(D\) はトーナメントなので \(F\cup T=V\setminus C\) も成り立つ。始頂点かつ終頂点である頂点は存在しないので、任意の終頂点は \(\mathbf{c}\) の全ての頂点からの弧を持ち、任意の始頂点は \(\mathbf{c}\) の全ての頂点への弧を持つ。
さらに、任意の終頂点 \(t\) から任意の始頂点 \(f\) への弧が存在できないことも分かる。実際、そのような弧が存在するなら、閉路 \(\mathbf{c}\) の適当な箇所 (例えば \(v_{1}\) と \(v_{2}\) の間) に \(t\) と \(f\) を追加することで \(\mathbf{c}\) を長くできてしまう。
まとめると、\(D\) の各頂点は共通要素を持たない三つの集合 \(C\), \(F\), \(T\) のいずれかに属し、\(T\) から \(F\) への弧は存在せず、\(T\) から \(C\) への弧は存在せず、\(C\) から \(F\) への弧も存在しない。このとき \(T\) に属する頂点から \(C\) に属する頂点への歩道は存在しない (\(T\) から抜け出す弧が存在しないため)。これは \(T\) が空集合でない限り \(D\) が強連結という仮定と矛盾するので、\(T\) は空集合である。同様に \(F\) も空集合でなければならない。よって \(F\cup T=V\setminus C\) より \(V\setminus C\) は空集合であり、ここから \(V = C\) が分かる。つまり、\(D\) の任意の頂点は閉路 \(\mathbf{c}\) に含まれる。言い換えれば \(\mathbf{c}\) はハミルトン閉路であり、Camion の定理は証明された。□
4.10.4 トーナメントを使った Vandermonde 行列式の導出
トーナメントに関する最後の話題として、トーナメントの興味深い応用の一つを簡単に紹介する: Vandermonde 行列式の組合せ論的な証明である。ここで省略される多くの詳細は [17s-lec8] から確認できる。
Vandermonde 行列式を思い出そう:
\(x_{1},x_{2},\ldots,x_{n}\) を \(n\) 個の実数 (より一般的に言えば、可換環の要素) とする。\(n \times n\) 行列 \(V\) を次のように定める:
このとき、\(V\) の行列式 \(\det V\) に関して次の等式が成り立つ:
この定理には様々な短い証明が知られている (例えば ProofWiki には、ここに示した \(V\) の転置行列に対する証明がいくつか掲載されている)。これから組合せ論的な証明の概略を示す。これは Ira Gessel による 1979 年の論文 [Gessel79] で示された証明である。
まず、\(\det V\) や \(\prod\limits_{1\leq i < j\leq n}\left( x_{i}-x_{j}\right) \) とトーナメントに何の関係があるのだろうか?
準備運動として次の積を考えよう。整数の組 \(\left( i,j\right) \) に対して \(y_{\left( i,j\right) }\) という数値が存在すると仮定している:
実際に展開すると \(8\) 個の項が得られる:
\(8\) 個の項が全て \(y_{a}y_{b}y_{c}\) の形をしていることに注目してほしい。ここで \(a\), \(b\), \(c\) に関して次の関係が成り立つ:
\(a\), \(b\), \(c\) は \(\left\{ 1,2,3\right\} \) を頂点集合とするトーナメントの弧と考えることができる。そうしたとき、最初に示した積は次のように変形できる:
参考のため、\(\left\{ 1,2,3\right\} \) を頂点集合とする \(8\) 個のトーナメント全てをここに示す:
分かりやすいように、\(i < j\) を満たす弧 \(ij\) は青、満たさない弧は赤としている。
この展開は一般化できる:
この式で \(y_{\left( i,j\right) } = \begin{cases} x_{j} & (i < j \text{ のとき})\\ -x_{j} & (i\geq j \text{ のとき})\end{cases}\) と置換すると、次の等式を得る:
ここで \(\deg^{-} j\) は頂点 \(j\) の入次数を表し、\(D\) の「赤い弧」は \(i > j\) を満たす \(D\) の弧 \(ij\) を表す。この和をこれから「ビッグサム」と呼ぶ。
一方、\(S_{n}\) を \(\left\{ 1,2,\ldots,n\right\} \) の置換群、\(\operatorname*{sign}\sigma\) を置換 \(\sigma\) の符号とすると、行列式の定義より次の等式が成り立つ:
この和を「スモールサム」と呼ぶ。
ビッグサムとスモールサムが等しいと示すことが目標となる。この証明は、次の点を確かめることで行われる:
-
スモールサムの各項に対応するビッグサムの項が存在する。つまり、各置換 \(\sigma\in S_{n}\) に対して次の等式が成り立つトーナメント \(T_{\sigma}\) が存在する:
\[ \left( -1\right) ^{\left(\text{\# } T_{\sigma}\, \text{の赤い弧}\right) }\prod\limits_{j=1}^{n}x_{j}^{\deg^{-}j}=\operatorname*{sign}\sigma\cdot \prod_{j=1}^{n}x_{j}^{\sigma\left( j\right) -1} \]この \(T_{\sigma}\) を見つけられるだろうか?
-
スモールサムの項に対応しないビッグサムの項は打ち消される。なぜだろうか?
「トーナメント \(D\) が対応するスモールサムの項を持たないなら、\(D\) は \(3\)-閉路 (長さが \(3\) の閉路) を持つ」を示すことが基本的なアイデアとなる。その \(3\)-閉路を反転させる (\(3\) 個の弧を反転させる) と、全ての頂点の入次数は変化せず \(\left( -1\right) ^{\left(\text{\# } D\, \text{の赤い弧}\right) }\) の符号が反転する (\(3\) 個の弧が逆向きになるため)。
これで「スモールサムに対応する項を持たないビッグサムの項それぞれに対して、その符号が反転した項がビッグサムに存在する」が示せた。しかし、これだけではスモールサムに含まれないビッグサムの項が全て打ち消されると言うことはできない: 例えば \(1+1+1+\left( -1\right) \) は \(0\) に等しくない。符号が正の (つまり \(\left( -1\right) ^{\left(\text{\# } D\, \text{ の赤い弧} \right) }=1\) の) 項が、絶対値が同じで符号が負の (つまり \(\left( -1\right) ^{\left(\text{\# } D\, \text{ の赤い弧} \right) }=-1\) の) 項と同じ個数だけ存在すると示す必要がある。
これを示す方法の一つとして、ビッグサムの「正の項」と「負の項」の間に全単射 (完全な対応関係) を構築する方法がある。ただ、これは難易度が高い: トーナメントには \(3\)-閉路が複数含まれる可能性があるので、どの \(3\)-閉路を反転させるかを考えなければならず、さらにその操作は全単射でなければならない (二つの「正の項」が同じ「負の項」に対応することがあってはいけない)。
これより間接的ではあるものの簡単な方法は次の通りである: 正の整数 \(k\) を固定し、ちょうど \(k\) 個の \(3\)-閉路を持つトーナメントだけを考える。そういったトーナメントのそれぞれについて、\(k\) 個の \(3\)-閉路のいずれかを反転させる。このとき \(3\)-閉路の個数は変化しないと示せる ので、\(k\) は変化しない。ここから、同じ絶対値を持つ「正の項」と「負の項」の間に一対一の対応関係が \(k\) ごとに存在すると分かる。つまり両者の個数は等しく、互いに打ち消し合う。後に残るのはスモールサムに存在する項のみとなる。
先述の通り、これは証明の粗い概略でしかない。詳細は [17s-lec8] から確認できる。
-
以降では空の列 \(\left( {}\right) \) が単純有向グラフ \(\left( \varnothing,\varnothing\right) \) のハミルトン路であると解釈して議論を進める。 ↩︎
-
ところで、ちょうど \(2\) 個の頂点を持つトーナメントは (弧を一つしか持たないので) 強連結となれない。そのため「\(D\) は \(2\) 個以上の頂点を持つ」と言った時点で \(D\) の頂点数が \(3\) 以上であることが保証される。 ↩︎
-
ここで添え字は \(k\) に関するモジュロを取ると定める。つまり \(v_{k+1}\) は \(v_{1}\) を意味する。 ↩︎