4.5. 歩道・路・閉歩道・閉路

目次

4.5.1定義

続いて単純有向グラフと多重有向グラフにおける様々な種類の歩道を定義する。

単純有向グラフにおける定義では、第 2.9 節と第 2.10 節で示した単純グラフにおける定義を参考にできる。通過する辺の向きが正しいことを要求する点だけに気を付ければよい:

定義 4.5.1

\(D\) を単純有向グラフとする。このとき:

  1. \(D\) における歩道 (walk) とは、\(D\) の頂点の有限列 \(\left( v_{0},v_{1},\ldots,v_{k}\right) \) (\(k \geq 0\)) であって、組 \(v_{0}v_{1},\ v_{1}v_{2},\ v_{2}v_{3},\ \ldots ,\ v_{k-1}v_{k}\) が全て \(D\) の弧であるものを言う (\(k = 0\) のとき後半の条件は空虚な真となる)。

  2. \(\mathbf{w}=\left( v_{0},v_{1},\ldots,v_{k}\right) \) を \(D\) における歩道とする。このとき:

    • \(\mathbf{w}\) の頂点 (vertex) は \(v_{0},v_{1},\ldots,v_{k}\) と定義される。

    • \(\mathbf{w}\) の弧 (arc) は組 \(v_{0}v_{1},\ v_{1}v_{2},\ v_{2}v_{3},\ \ldots,\ v_{k-1}v_{k}\) と定義される。

    • 非負整数 \(k\) を \(\mathbf{w}\) の長さ (length) と呼ぶ。 [歩道 \(\mathbf{w}\) の長さは \(\mathbf{w}\) の弧の個数に等しく、\(\mathbf{w}\) の頂点の個数より \(1\) だけ小さい。ここで重複する弧/頂点は別のものとして数える。]

    • 頂点 \(v_{0}\) を \(\mathbf{w}\) の始点 (starting point) と呼ぶ。\(\mathbf{w}\) を「\(v_{0}\) から始まる歩道」と言う。

    • 頂点 \(v_{k}\) を \(\mathbf{w}\) の終点 (ending point) と呼ぶ。\(\mathbf{w}\) を「\(v_{k}\) で終わる歩道」と言う。

  3. \(D\) における路 (path) とは、異なる頂点からなる \(D\) における歩道を言う。言い換えれば、路は \(v_{0},v_{1},\ldots,v_{k}\) が相異なる歩道 \(\left( v_{0},v_{1},\ldots,v_{k}\right) \) を意味する。

  4. \(p\) と \(q\) を \(D\) の二頂点とする。\(p\) から \(q\) への歩道 (walk from \(p\) to \(q\)) とは、\(p\) から始まって \(q\) で終わる歩道を言う。\(p\) から \(q\) への路 (path from \(p\) to \(q\)) とは、\(p\) から始まって \(q\) で終わる路を言う。

  5. \(D\) の閉歩道 (closed walk) とは、始点と終点が同じ歩道を言う。言い換えれば、\(w_{0}=w_{k}\) を満たす歩道 \(\left( w_{0},w_{1},\ldots,w_{k}\right) \) を閉歩道と呼ぶ。本書では閉歩道を回路 (circuit) とも呼ぶ (ただし、回路を閉歩道と少しだけ異なる歩道として定義する文献も多い)。

  6. \(D\) の閉路 (cycle) とは、閉歩道 \(\left( w_{0},w_{1},\ldots,w_{k}\right) \) であって「\(k \geq 1\)」と「頂点 \(w_{0}\), \(w_{1}\), \(\ldots\), \(w_{k-1}\) が相異なる」を満たすものを言う。

単純グラフにおける閉路の定義に存在した「\(k \geq 3\)」の条件が単純有向グラフでは「\(k \geq 1\)」になっていることに注意してほしい。単純有向グラフはループを持てるためである。また、幸い弧には向きがあるので、同じ弧を通って行って返る歩道を考える必要はない。そのため単純グラフの閉路の定義に存在した追加の条件は削除できる。

例 4.5.2

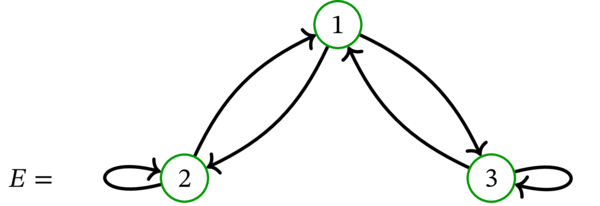
次の単純有向グラフ \(D\) を考える:

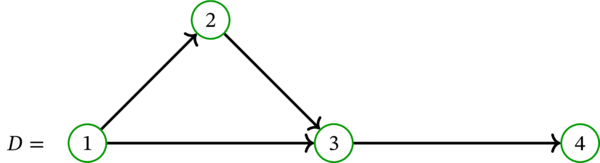
このとき \(\left( 1,2,3,4\right) \) と \(\left( 1,3,4\right) \) はどちらも \(D\) の歩道であり、路でもある。しかし \(\left( 2,3,1\right) \) は歩道でない (\(3\) から \(1\) に移動するとき弧 \(31\) は使用できない)。この有向グラフ \(D\) は閉路を持たない。\(D\) が持つ唯一の閉歩道は長さが \(0\) の歩道である。

例 4.5.3

次の単純有向グラフ \(D\) を考える:

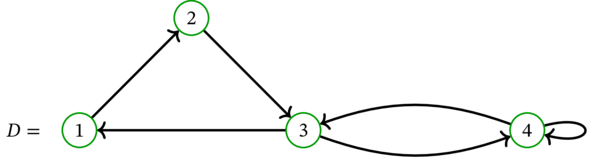
このとき \(\left( 1,2,3,1\right) \)と \(\left( 3,4,3\right) \) と \(\left( 4,4\right) \) はどれも \(D\) の閉路である。また、\(\left( 1,2,3,4,3,1\right) \) は閉歩道であって閉路でない。

次は同様の概念を多重有向グラフに対しても定義しよう。ここでは定義 3.1.4 で示した多重グラフに対する定義が参考になる:

定義 4.5.4

\(D=\left( V,A,\psi\right) \) を多重有向グラフとする。このとき:

  1. \(D\) における歩道 (walk) とは、次の形をした列を言う:

    \[ \left( v_{0},a_{1},v_{1},a_{2},v_{2},\ldots,a_{k},v_{k}\right) \ \ \ \ \ \ \ \ \ \ \left( k \geq0\right) \]

    ここで \(v_{0},v_{1},\ldots,v_{k}\) は全て \(D\) の頂点、\(a_{1},a_{2},\ldots,a_{k}\) は全ての \(G\) の弧であり、全ての \(i\in\left\{ 1,2,\ldots,k\right\} \) は次の条件を満たす:

    \[ \psi\left( a_{i}\right) =\left( v_{i-1},v_{i}\right) \]

    [つまり、\(a_{i}\) の始点が \(v_{i-1}\) で、\(a_{i}\) の終点が \(v_{i}\) である必要がある。なお、歩道に頂点と弧が両方とも含まれるのは、二頂点間を「移動」するときに使う弧を歩道から分かるようにするためである。]

    歩道 \(\left( v_{0},a_{1},v_{1},a_{2},v_{2},\ldots,a_{k},v_{k}\right) \) の頂点 (vertex) とは \(v_{0},v_{1},\ldots,v_{k}\) を指し、この歩道の弧 (arc) とは \(a_{1},a_{2},\ldots,a_{k}\) を指す。また、この歩道は \(v_{0}\) から始まり、\(v_{k}\) で終わると言う。さらに、この歩道を \(v_{0}\) から \(v_{k}\) への歩道 (walk from \(v_{0}\) to \(v_{k}\)) と呼ぶ。この歩道の始点 (starting point) とは \(v_{0}\) を指し、終点 (ending point) とは \(v_{k}\) を指す。

  2. 頂点が全て異なる歩道を路 (path) と呼ぶ。

  3. \(v_{k}=v_{0}\) を満たす歩道 \(\left( v_{0},a_{1},v_{1},a_{2},v_{2},\ldots,a_{k},v_{k}\right) \) を閉歩道 (closed walk) と呼ぶ。閉歩道は回路 (circuit) とも呼ばれる。

  4. 次の条件を満たす閉歩道 \(\left( v_{0},a_{1},v_{1},a_{2},v_{2},\ldots,a_{k},v_{k}\right) \) を閉路 (cycle) と呼ぶ:

    • 頂点 \(v_{0},v_{1},\ldots,v_{k-1}\) が相異なる。

    • \(k \geq 1\) が成り立つ。

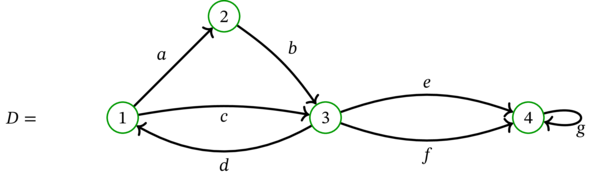
    [弧 \(a_{i}\) の始点は \(v_{i-1}\) なので、一つ目の条件が成り立つとき \(a_{1},a_{2},\ldots,a_{k}\) は相異なる。]

例 4.5.5

\(D\) を次の多重有向グラフとする:

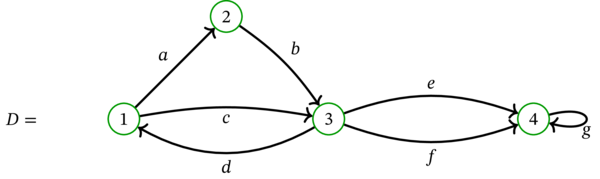
このとき \(\left( 1,a,2,b,3,d,1\right) \) と \(\left( 3,d,1,c,3\right) \) と \(\left( 4,g,4\right) \) はどれも \(D\) の閉路である。これに対して、\(\left( 3,d,1,a,2,b,3,d,1,c,3\right) \) は閉歩道ではあるものの閉路ではない。

4.5.2基本的な性質

続いて、これまでに見てきた歩道・路・閉歩道・閉路の性質の中で有向グラフでも成り立つのはどれかを考えよう。

命題 2.9.3 では、ある歩道の終点が別の歩道の始点となっているとき、その二つの歩道を「連結」できることを示した。この結果は命題 3.3.7 で多重グラフに拡張された。同じことは多重有向グラフでも言える:

命題 4.5.6

\(D\) を多重有向グラフ、\(u\), \(v\), \(w\) を \(D\) の三頂点とする。\(\mathbf{a}=\left( a_{0},e_{1},a_{1},\ldots ,e_{k},a_{k}\right) \) が \(u\) から \(v\) への歩道で、\(\mathbf{b}=\left( b_{0},f_{1},b_{1},\ldots,f_{\ell},b_{\ell}\right) \) が \(v\) から \(w\) への歩道なら、次の列は \(u\) から \(w\) への歩道である:

\[ \begin{aligned} & \left( a_{0},e_{1},a_{1},\ldots,e_{k},a_{k},f_{1},b_{1},f_{2},b_{2},\ldots,f_{\ell},b_{\ell}\right) \\ & \quad =\left( a_{0},e_{1},a_{1},\ldots,a_{k-1},e_{k},b_{0},f_{1},b_{1},\ldots,f_{\ell},b_{\ell}\right) \\ & \quad =\left( a_{0},e_{1},a_{1},\ldots,a_{k-1},e_{k},v,f_{1},b_{1},\ldots,f_{\ell},b_{\ell}\right) \end{aligned} \]

この歩道を今後 \(\mathbf{a}\ast\mathbf{b}\) と表記する。

[証明] 無向グラフに対する (自明な) 議論がここでも利用できる。□

一方、無向グラフと異なり有向グラフでは歩道や路を反転できない。そのため、\(u\) から \(v\) への歩道があるのに対して \(v\) から \(u\) への歩道は存在しない、という状況がよく発生する。

単純グラフ (命題 2.9.5) と多重グラフ (命題 3.3.9) の両方で可能だった歩道から路を得る操作は多重有向グラフでも行える:

命題 4.5.7

\(D\) を多重有向グラフ、\(u\), \(v\) を \(D\) の二頂点、\(\mathbf{a}\) を \(u\) から \(v\) への歩道、\(k\) を \(\mathbf{a}\) の長さとする。このとき \(\mathbf{a}\) が路でないなら、長さが \(k\) より小さい \(u\) から \(v\) への歩道が存在する。

系 4.5.8

[歩道あるところに路あり] \(D\) を多重有向グラフ、\(u\), \(v\) を \(D\) の二頂点とする。\(u\) から \(v\) への長さ \(k \in \mathbb{N}\) の歩道が存在するなら、長さ \(k\) 以下の \(u\) から \(v\) への路が存在する。

この二つの事実は多重グラフと同様に証明できる。

次の命題は多重有向グラフに対する命題 2.10.4 である:

命題 4.5.9

\(D\) を多重有向グラフ、\(\mathbf{w}\) を \(D\) の歩道とする。\(\mathbf{w}\) は路であるか、そうでないなら閉路を含む (\(D\) の閉路であって全ての弧が \(\mathbf{w}\) の弧であるものが存在する)。

[証明] 命題 2.10.4 と同じ議論で証明できる。□

多重グラフ \(D\) と \(D\) の二頂点 \(u\), \(v\) が与えられたとき、第 2.9.4 項 で考えた五つのアルゴリズム的問題を考えることができる。多重グラフと同様に、この新しい設定でも以前に示した解答を利用できる。ただし「\(v\) の隣接頂点」は「\(v\) の入隣接頂点 (in-neighbor, \(D\) が \(w\) から \(v\) への弧を持つような頂点 \(w\))」に置き換える必要がある。また、歩道と路に弧を記録する必要もある。

4.5.3練習問題

練習問題 4.1

少なくとも一つの頂点を持つ多重有向グラフを \(D\) とする。次の命題を証明せよ:

  1. \(D\) の任意の頂点 \(v\) が \(\deg^{+} v > 0\) を満たすなら、\(D\) は閉路を持つ。

  2. \(D\) の任意の頂点 \(v\) が \(\deg^{+}v=\deg ^{-}v=1\) を満たすなら、\(D\) の各頂点はちょうど一つの \(D\) の閉路に属する。ただし、ある閉路を回転させて得られる閉路は全て同じ閉路とみなす。

練習問題 4.2

\(p\) を素数、\(\left( a_{1},a_{2},a_{3},\ldots\right) \) を周期 \(p\) を持つ周期的な無限整数列とする (つまり、全ての \(i > 0\) に対して \(a_{i} = a_{i+p}\) が成り立つ)。\(a_{1}+a_{2}+\cdots+a_{p}\) が \(p\) で割り切れないと仮定する。次に示す \(p\) 個の整数がどれも \(p\) で割り切れないような \(i\in\left\{ 1,2,\ldots,p\right\} \) が存在することを示せ:

\[ a_{i},\ a_{i}+a_{i+1},\ a_{i}+a_{i+1}+a_{i+2},\ \ldots,\ a_{i}+a_{i+1}+\cdots+a_{i+p-1} \]

[これは \(i\leq j < i+p\) に対する \(p\) 個の和 \(\displaystyle \sum_{k=i}^{j} a_k = a_{i}+a_{i+1}+\cdots+a_{j}\) である。]

[Remark: この命題は \(p\) が素数でなければ成り立たない。例えば \(p=4\) のときは \(( 0,2,2,2,\) \(0,2,2,2,\ldots) \) が反例となる。]

[ヒント: 練習問題 4.1 (a) を使う。どんな有向グラフを考えるべきだろうか？ なぜ閉路を持つのだろうか？]

練習問題 4.3

\(D=\left( V,A,\psi\right) \) を多重有向グラフとする。

\(D\) の二頂点 \(u\), \(v\) に対して、\(D\) に \(u\) から \(v\) への路が存在するとき \(u\overset{\ast }{\rightarrow}v\) と表記する。

\(D\) の根 (root) とは、任意の頂点 \(v \in V\) が \(u\overset{\ast}{\rightarrow}v\) を満たすような頂点 \(u \in V\) を言う。

二頂点 \(u\), \(v\) の共通祖先 (common ancestor) とは、\(w\overset{\ast}{\rightarrow}u\) と \(w\overset{\ast}{\rightarrow}v\) を満たす頂点 \(w \in V\) を言う。

\(D\) が少なくとも一つの頂点を持つとする。\(D\) が根を持つのは \(D\) の任意の二頂点が共通祖先を持つとき、かつそのときに限ると示せ。

次の練習問題では Mantel の定理 (定理 2.4.6) を有向グラフに対応させて一般化した命題を証明する:

練習問題 4.4

\(D\) を単純有向グラフとする。\(D\) は \(n\) 個の頂点と \(a\) 個の弧を持ち、ループを持たないと仮定する。\(a > n^{2}/2\) が成り立つとき、次の命題を示せ:

  1. \(D\) は長さが \(3\) の閉路を持つ。

  2. \(D\) は強い \(3\)-閉路を持つ。ここで強い \(3\)-閉路 (enhanced 3-cycle) とは、相異なる頂点の三つ組 \(\left( u,v,w\right) \) であって四つの組 \(\left( u,v\right) \), \(\left( v,w\right) \), \(\left( w,u\right) \), \(\left( u,w\right) \) が全て \(D\) の弧であるものを言う。

練習問題 4.5

閉路を持たない単純有向グラフを \(D=\left( V,A\right) \) とする。

\(\mathbf{v} = \left( v_{1}, v_{2}, \ldots, v_{n} \right) \) を \(D\) の頂点の列とする。 [\(\mathbf{v}\) は歩道とは限らない！] このとき \(\mathbf{v}\) のバックカット (back-cut) とは、始点 \(v_{i}\) と終点 \(v_{j}\) を持つ弧 \(a \in A\) であって \(j < i\) を満たすものを言う。 [数学的でない言い方をすれば、\(\mathbf{v}\) の頂点からそれより前にある \(\mathbf{v}\) の頂点への \(D\) の弧を \(\mathbf{v}\) のバックカットと言う。]

\(D\) の頂点の列 \(\mathbf{v}=\left( v_{1},v_{2},\ldots,v_{n}\right) \) がトポソート (toposort)1であるとは、\(D\) の各頂点がちょうど一度ずつ \(\mathbf{v}\) に含まれ、かつ \(\mathbf{v}\) がバックカットを持たないことを言う。

次の命題を示せ:

  1. \(D\) は少なくとも一つのトポソートを持つ。

  2. \(D\) のトポソートが一つしか存在しないなら、そのトポソートは \(D\) のハミルトン路である。

    ここでハミルトン路とは \(D\) の歩道であって \(D\) の各頂点をちょうど一度ずつ含むものを言う。

[例: 次の有向グラフを \(D\) とする:

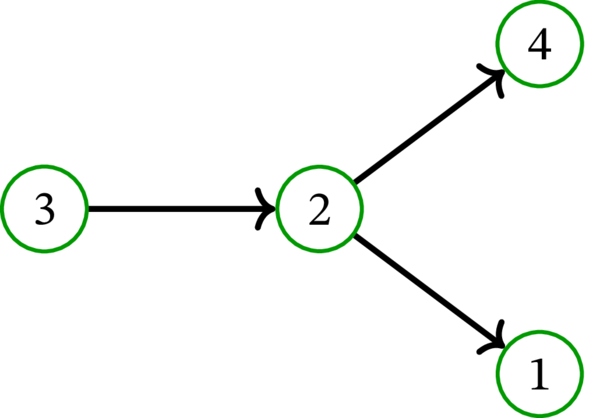
\(D\) は \(\left( 3,2,1,4\right) \) と \(\left( 3,2,4,1\right) \) という二つのトポソートを持つ。]

練習問題 4.6

\(n\) を正整数、\(D\) を長さ \(2\) 以下の閉路を持たない有向グラフとする。\(D\) が \(2^{n}-1\) 個以上の頂点を持つとき、\(D\) は \(n\) 個の頂点を持ち閉路を含まない誘導部分有向グラフを持つことを示せ。

4.5.4隣接行列

多重有向グラフにおいて特定の頂点間に存在する歩道の個数を計算する方法が行列代数によって提供される:

定理 4.5.10

\(D=\left( V,A,\psi\right) \) を多重有向グラフとする。ある \(n\in\mathbb{N}\) で \(V=\left\{ 1,2,\ldots,n\right\} \) だと仮定する。

任意の行列 \(M\) と正整数 \(i\), \(j\) に対して、\(M\) の \(\left( i,j\right) \) 要素 (\(i\) 行 \(j\) 列成分) を \(M_{i,j}\) と表す。

次の等式で定義される \(n \times n\) 行列を \(C\) とする:

\[ C_{i,j} = \left(\text{始点が } i \text{ で終点が } j \text{ である弧 } a \in A \text{ の個数}\right) \quad \left(\forall i,j\in V\right) \]

任意の \(k\in\mathbb{N}\) と \(i,j\in V\) に対して、始点 \(i\) と終点 \(j\) を持つ長さ \(k\) の \(D\) の歩道はちょうど \(\left( C^{k}\right) _{i,j}\) 個だけ存在する。

Remark 4.5.11

定理 4.5.10 の行列 \(C\) は \(D\) の隣接行列 (adjacency matrix) と呼ばれる。例えば、\(D\) を次の多重有向グラフとする:

このとき \(D\) の隣接行列 \(C\) は次の行列である:

\[ C= \begin{pmatrix} 0 & 1 & 1 & 0\\ 0 & 0 & 1 & 0\\ 1 & 0 & 0 & 2\\ 0 & 0 & 0 & 1 \end{pmatrix} \]

多重有向グラフ \(D\) の隣接行列が与えられれば、辺の識別子を除く \(D\) に関する全ての情報をそこから復元できる。そのため隣接行列は多重有向グラフをエンコードする手軽な手段としてよく使われる。

[定理 4.5.10 の証明] 問題の設定にある \(i\), \(j\), \(k\) のことは一旦忘れる。証明したいのは次の命題である:

Claim 1: 任意の \(i \in V\), \(j \in V\), \(k \in \mathbb{N}\) に対して、次の等式が成り立つ:
\[ \left( C^{k}\right) _{i,j}=\left(i \text{ から } j \text{ への長さ } k \text{ の歩道の個数} \right) \]

Claim 1 を証明する前に次の点を確認しておく。\(C\) は \(D\) の隣接行列だから、隣接行列の定義より、任意の \(i \in V\) と \(j \in V\) に対して次の等式が成り立つ:

\[ C_{i,j}=\left( \text{始点 \(i\) と終点 \(j\) を持つ弧 \(a\in A\) の個数}\right) \]

これを言い換えれば、任意の \(i \in V\) と \(j \in V\) に対して次の等式が成り立つ:

\[ C_{i,j}=\left(\text{\(i\) から \(j\) への弧の個数}\right) \]

ここで \(i\) から \(j\) への弧 (arc from \(i\) to \(j\)) とは、始点が \(i\) で終点が \(j\) の弧 \(a \in A\) を意味する。

\(i\) を \(w\) に書き換えると、次の事実を得る: 任意の \(w\in V\) と \(j \in V\) に対して、

\[ C_{w,j}=\left(\text{\(w\) から \(j\) への弧の個数} \right) \]

が成り立つ。

また、行列の乗算の定義より、\(M\), \(N\) を \(n\times n\) 行列とするとき任意の \(i \in V\), \(j \in V\) に対して次の等式が成り立つ:

\[ \left( MN\right) _{i,j}=\sum_{w=1}^{n}M_{i,w}N_{w,j}\qquad (1) \]

これで Claim 1 を証明する準備が整った。これから Claim 1 を \(k\) に関する数学的帰納法で示す。

ベースケース: \(k=0\) の場合に命題が正しいことをまず示す。

任意に \(i \in V\) と \(j \in V\) を取る。\(n\times n\) 行列の \(0\) 乗は \(n\times n\) の恒等行列 \(I_{n}\) と定義されるので、\(C^{0} = I_{n}\) である。よって恒等行列の定義より次の等式が成り立つ:

\[ \begin{cases} \left( C^{0}\right) _{i,j}=\left( I_{n}\right) _{i,j}=1 & \left(i = j \text{ のとき}\right) \\ 0 & \left(i \neq j \text{ のとき}\right) \end{cases}\qquad (2) \]

一方、\(i\) から \(j\) への長さ \(0\) の歩道はいくつあるだろうか？ 長さ \(0\) の歩道は単一の頂点だけから構成され、その頂点が歩道の始点かつ終点となる。つまり、\(i\) から \(j\) への長さ \(0\) の歩道は \(i = j\) のときに限って存在し、そのような歩道は \(\left( i\right) \) の一つしか存在しない。よって次の等式が成り立つ:

\[ \left( \text{\(i\) から \(j\) への長さ \(0\) の歩道の個数} \right) = \begin{cases} 1 & \left(i=j \text{ のとき}\right)\\ 0 & \left(i\neq j \text{ のとき} \right) \end{cases} \]

これを式 \((2)\)と比較すると次の等式を得る:

\[ \left( C^{0}\right) _{i,j} =\left(\text{\(i\) から \(j\) への長さ \(0\) の歩道の個数}\right) \]

この等式は任意の \(i \in V\) と \(j \in V\) に対して成り立つ。言い換えれば、Claim 1 は \(k=0\) の場合に成り立つ。これでベースケースは証明できた。

帰納ステップ: \(g\) を正整数とする。Claim 1 が \(k = g-1\) のとき成り立つと仮定して、Claim 1 が \(k = g\) のとき成り立つと示す。

Claim 1 が \(k=g-1\) のとき成り立つという仮定を言い換えれば、任意の \(i \in V\) と \(j \in V\) に対して次の等式が成り立つ:

\[ \left( C^{g-1}\right) _{i,j}= \left( \text{\(i\) から \(j\) への長さ \(g-1\) の歩道の個数} \right) \]

\(i\) から \(j\) への長さ \(g\) の歩道はどれも次の形をしている:

\[ \mathbf{w}=\left( v_{0},a_{1},v_{1},a_{2},v_{2},\ldots,a_{g-1},v_{g-1}, a_{g},v_{g}\right) \]

ここで \(v_{0},v_{1},\ldots,v_{g}\) は \(D\) の頂点、\(a_{1},a_{2},\ldots,a_{g}\) は \(D\) の弧を表す。さらに \(v_{0}=i\) と \(v_{g}=j\) が成り立ち、全ての \(i \in \left\{ 1,2,\ldots,g\right\} \) で \(\psi\left( a_{h}\right) =\left( v_{h-1},v_{h}\right)\) が成り立つ。よって、こういった歩道 \(\mathbf{w}\) は全て次のアルゴリズムで構築できる:

逆に、このアルゴリズムが必ず \(i\) から \(j\) への長さ \(g\) の歩道を構築し、アルゴリズム中で異なる選択をすれば異なる歩道が手に入ることは容易に分かる。よって \(i\) から \(j\) への長さ \(g\) の歩道の個数は、このアルゴリズムで構築できる歩道の個数に等しい。アルゴリズムの中で選択肢の中から自由に選択できる箇所に注目すれば、後者が \(\displaystyle \sum_{w\in V}\left( C^{g-1}\right) _{i,w}C_{w,j}\) に等しいと分かる (最初に \(w \in V\) の選択があり、その後 \(w\) に応じて \(\left( C^{g-1}\right) _{i,w}\) 個の選択肢と \(C_{w,j}\) 個の選択肢がある)。よって、\(i\) から \(j\) への長さ \(g\) の歩道の個数は \(\displaystyle \sum_{w\in V}\left( C^{g-1}\right) _{i,w}C_{w,j}\) である。これを数式で書けば次のようになる:

\[ \left( \text{\(i\) から \(j\) への長さ \(g\) の歩道の個数}\right) =\sum_{w\in V}\left( C^{g-1}\right) _{i,w}C_{w,j} \]

一方、次の等式も成り立つ:

\[ \begin{aligned} \left( C^{g} \right) _{i,j} & =\left( C^{g-1}C\right) _{i,j}\\ & =\sum_{w=1}^{n}\left( C^{g-1}\right) _{i,w}C_{w,j}\\ & \qquad \left( \text{式 (1) で \(M=C^{g-1}\), \(N=C\) とした} \right) \\[7.5pt] & =\sum_{w\in V}\left( C^{g-1}\right) _{i,w}C_{w,j}\\ & \qquad \left(\because\ \left\{ 1,2,\ldots,n\right\} =V\right) \end{aligned} \]

二つの等式を比較すれば次を得る:

\[ \left( C^{g}\right) _{i,j}= \left(\text{\(i\) から \(j\) への長さ \(g\) の歩道の個数}\right) \]

この等式は任意の \(i \in V\) と \(j \in V\) に対して成り立つ。言い換えれば、Claim 1 は \(k=g\) のとき成り立つ。以上で再帰ステップが完了したので、数学的帰納法より Claim 1 は証明された。

定理 4.5.10 は Claim 1 から直ちに従う。□

練習問題 4.7

\(E\) を次の多重有向グラフとする:

任意の \(n \in \mathbb{N}\) に対して、\(1\) から \(1\) への長さ \(n\) の歩道の個数を計算せよ。

  1. トポソートは「トポロジカルソート」の略である。この名前で呼ばれている理由を私は知らない。 ↩︎

広告
このページの文章はテキストゆれないくんを使って校正されました。