9.1. ネットワークとフローの定義
9.1.1 ネットワーク
本書では \(\mathbb{N}=\left\{ 0,1,2,\ldots\right\} \) だったことを思い出してほしい。
ネットワーク (network) は次の要素から構成される:
-
多重グラフ \(D=\left( V,A,\psi\right) \)
-
入口 (source) と呼ばれる頂点 \(s \in V\)
-
出口 (sink) と呼ばれる \(s\) と異なる頂点 \(t \in V\)
-
容量関数 (capacity function) と呼ばれる関数 \(c\colon A\rightarrow\mathbb{N}\)
ネットワークの例を示す:
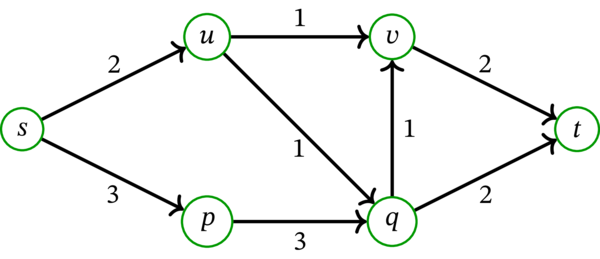
ここで \(D\) は描画されているグラフである (ループと多重辺を持たないので、弧にはラベルを付けていない)。頂点 \(s\), \(t\) は図中で \(s\), \(t\) とラベルの付いた頂点であり、関数 \(c\) の値は \(D\) の弧上に書かれている (例えば \(c\left( \left( s,p\right) \right) =3\) や \(c\left( \left( u,q\right) \right) =1\) が成り立つ)。
例 9.1.2 の有向グラフ \(D\) は閉路を持たず、\(\deg^{-}s=\deg^{+}t=0\) を満たす。この条件はネットワークの定義に含まれないものの、基礎的な応用の多くで満たされる。
また、例 9.1.2 では全ての容量 (容量関数の値) が正である。この条件もネットワークの定義には含まれない。しかし、多くの応用では容量が \(0\) の辺は意味を持たないので、そういった辺は無視しても問題ない。
ここで定義したネットワークは、数学の様々な分野に存在するネットワークと名の付く概念の一つに過ぎない。そういったネットワークの多くは大まかに捉えれば「何らかの構造を持ったグラフ」であるものの、共通点は少ない。
9.1.2 \(\overline{S}\), \(\left[ P,Q\right] \), \(d\left( P,Q\right) \) の定義
多重有向グラフ \(D=\left( V,A,\psi\right) \)、入口 \(s \in V\)、出口 \(t \in V\)、容量関数 \(c\colon A\rightarrow\mathbb{N}\) から構成されるネットワークを \(N\) とする。このとき:
-
任意の弧 \(a \in A\) に対して、値 \(c\left( a\right) \in\mathbb{N}\) を弧 \(a\) の容量 (capacity) と呼ぶ。
-
\(V\) の任意の部分集合 \(S\) に対して、\(V\) の部分集合 \(V\setminus S\) を \(\overline{S}\) と表記する。
-
\(V\) の任意の部分集合 \(P\), \(Q\) に対して、\(P\) に属する始点と \(Q\) に属する終点を持つ辺全体の集合を \(\left[ P,Q\right] \) と表記する。つまり、次のように定める:
\[ \left[ P,Q\right] \colonequals \left\{ a\in A\mid \psi\left( a\right) \in P\times Q\right\} \] -
\(V\) の任意の部分集合 \(P\), \(Q\) と任意の関数 \(d\colon A\rightarrow\mathbb{N}\) に対して、値 \(d\left( P,Q\right) \in\mathbb{N}\) を次のように定義する:
\[ d\left( P,Q\right) \colonequals \sum_{a\in\left[ P,Q\right] }d\left( a\right) \]
例 9.1.2 のネットワークをもう一度考える。\(V\) の部分集合 \(\left\{ s,u\right\} \) に対して次の等式が成り立つ:
また、次の等式も成り立つ:
\(\left\{ s,u\right\} \) と \(\overline{\left\{ s,u\right\} }\) の「境界」をネットワークの描画に加えると、この等式を視覚的に表現できる:
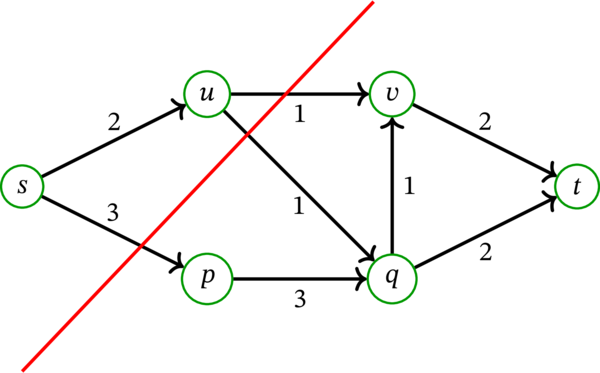
赤い線で書かれた「境界」の左側が \(\left\{ s,u\right\} \) であり、右側が \(\overline{\left\{ s,u\right\} }\) である。この境界を \(\left\{ s,u\right\} \) 側から \(\overline{\left\{ s,u\right\} }\) 側へと横断する辺全体の集合が \(\left[ \left\{ s,u\right\},\,\overline{\left\{ s,u\right\} }\right] \) に等しい。
\(D=\left( V,A,\psi\right) \) を平衡な多重有向グラフとする。\(V\) の任意の部分集合 \(S\) に対して、\(\overline{S}\colonequals V\setminus S\) と定める。\(V\) の任意の部分集合 \(S\), \(T\) に対して、\(\left[ S,T\right]\) を次のように定める:
\(V\) の任意の部分集合 \(S\) に対して \(\left\vert \left[ S,\overline{S}\right] \right\vert =\left\vert \left[ \overline{S},S\right] \right\vert \) だと示せ。
9.1.3 フロー
続いてネットワーク上のフローを定義する:
多重有向グラフ \(D=\left( V,A,\psi\right) \)、入口 \(s \in V\)、出口 \(t \in V\)、容量関数 \(c\colon A\rightarrow\mathbb{N}\) から構成されるネットワークを \(N\) とする。
ネットワーク \(N\) 上のフロー (flow) とは、次の条件を満たす関数 \(f\colon A\rightarrow \mathbb{N}\) を意味する:
-
任意の弧 \(a \in A\) で \(0\leq f\left( a\right) \leq c\left( a\right) \) が成り立つ。この条件は容量制約 (capacity constraints) と呼ばれる (弧 \(a \in A\) ごとに制約があるので、複数形を用いる)。
-
任意の頂点 \(v\in V\setminus\left\{ s,t\right\} \) が次の等式を満たす:
\[ f^{-}\left( v\right) = f^{+}\left( v\right) \]ここで \(f^{-}\) と \(f^{+}\) は次のように定義される:
\[ f^{-}\left( v\right) \colonequals \hspace{-8pt} \sum_{\substack{a\in A;\\[2pt] a \text{ の終点は } v}} \hspace{-10pt} f\left( a\right) \qquad \quad f^{+}\left( v\right) \colonequals \hspace{-8pt} \sum_{\substack{a\in A;\\[2pt] a \text{ の始点は } v}} \hspace{-10pt} f\left( a\right) \]この条件は保存制約 (conservation constraints) と呼ばれる。
フロー \(f\colon A\rightarrow\mathbb{N}\) と弧 \(a \in A\) に対して、値 \(f\left( a\right) \) を \(a\) における \(f\) の弧流量 (arc flow) と呼ぶ。
本書でネットワーク \(N\) 上のフロー \(f\) を描画するときは、ネットワークの描画と同様に \(N\) を構成する多重有向グラフを描画し、その上で各辺 \(a \in A\) の上に (容量 \(c\left( a\right) \) ではなく)「\(f\left( a\right)\, \) of \(\,c\left( a\right) \)」と書く。例 9.1.2 のネットワーク上のフロー \(f\) の描画を示す:
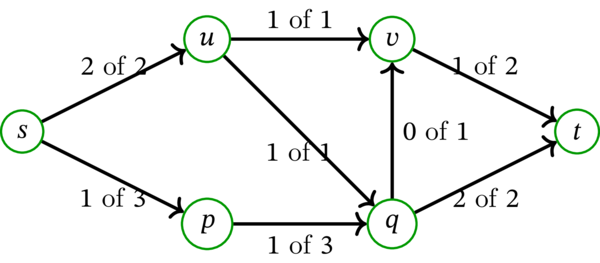
同じネットワーク上の異なるフロー \(g\) を考えることもできる:
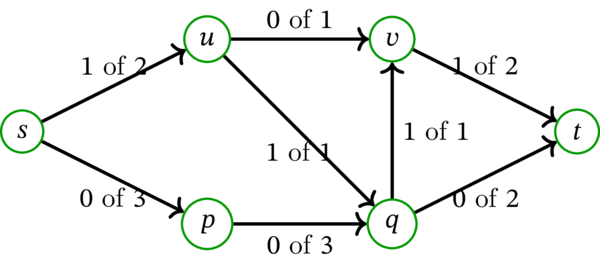
ネットワーク \(N\) と \(N\) 上のフローを直感的に捉える方法はいくつかある:
-
ネットワーク \(N\) は一方通行の道路の集まりを表すと考えることもできる: それぞれの弧 \(a \in A\) は一方通行の道路であり、容量 \(c\left( a\right) \) は一時間ごとに道路 \(a\) を通れる車の (最大) 台数に等しい。\(N\) 上のフロー \(f\) はそれぞれの道路を実際に通った車の台数を表す。フローの保存制約は \(s\) と \(t\) を除く任意の頂点 \(v\) に向かう車両の台数が \(v\) を離れる車両の台数に等しいと主張する (つまり、交通は \(s\) と \(t\) でのみ発生/消滅する)。
-
ネットワーク \(N\) はパイプの集まりを表すと考えることもできる: それぞれの弧 \(a \in A\) はパイプであり、\(c\left( a\right) \) は一秒間にパイプを通して輸送できる液体の量に等しい。\(N\) 上のフロー \(f\) はパイプ中を流れる液体の量を表し、パイプ \(a\) を一秒間に流れる量が \(f\left( a\right) \) で表される。フローの容量制約は容量より多い量の液体が流れるパイプ、そして負の容量の液体が流れるパイプがどちらも存在しないと主張する。また、フローの保存制約は \(s\) と \(t\) を除く任意の頂点 \(v\) に流入する液体の量 \(f^{-}\left( v\right) \) が \(v\) から流出する液体の量 \(f^{+}\left( v\right) \) に等しいと主張する。つまり、\(s\) と \(t\) 以外の箇所で液体が漏れ出たり足されたりすることはない。\(s\) が入口 (source) と呼ばれ、\(t\) が出口 (sink) と呼ばれる理由がこれで納得できるだろう。この例の不自然な点としては、パイプに方向があり、特定の方向 (始点から終点に向かう方向) にだけ液体が流れることがある。ただ、逆方向のパイプの組を使えば「無向」パイプをモデル化できる。
-
ネットワーク \(N\) は送金スキームを表すと考えることもできる: 各頂点 \(v \in V\) は銀行口座であり、このネットワークは \(s\) から \(t\) に資金を移動させるために存在する。\(s\) と \(t\) 以外の頂点 \(v\) は仲介口座であり、それぞれの弧 \(a \in A\) は始点の口座から終点の口座へ送金可能な最大金額を表す。\(N\) 上のフロー \(f\) は \(s\) から \(t\) に資金を移動させる方法を表し、任意の頂点 \(v\in V\setminus\left\{ s,t\right\} \) に対応する仲介口座は受け取った金額と同額を送金する。
言うまでもなく、こういった例は直感的にフローを理解するためだけにある。現実世界の応用で用いられるフローはここで紹介したフローといくらか異なる。
ネットワーク \(N\) 上のフローはネットワークを構成する多重有向グラフ \(D\) の路を一般化した概念とみなせる。実際、ネットワーク \(N\) を構成する多重有向グラフ \(D=\left( V,A,\psi\right) \) における \(s\) から \(t\) への路を \(\mathbf{p}\) とするとき、\(N\) 上のフロー \(f_{\mathbf{p}}\) を次のように定義できる:
ここでは \(\mathbf{p}\) の全ての弧が \(1\) 以上の容量を持つと仮定している。例 9.1.7 のフロー \(g\) はそのようなフローの例である。
9.1.4 入流量、出流量、フローの値
続いて、ネットワーク上のフローに関連付く値を定義する:
多重有向グラフ \(D=\left( V,A,\psi\right) \)、入口 \(s \in V\)、出口 \(t \in V\)、容量関数 \(c\colon A\rightarrow\mathbb{N}\) から構成されるネットワークを \(N\) とする。\(f\colon A\rightarrow\mathbb{N}\) を任意の写像 (例えば \(N\) 上のフロー) とする。このとき:
-
任意の頂点 \(v \in V\) に対して、\(f^{-}\left( v\right)\) と \(f^{+}\left( v\right)\) を次のように定める:
\[ f^{-}\left( v\right) \colonequals \hspace{-8pt} \sum_{\substack{a\in A;\\[2pt] a \text{ の終点は } v}} \hspace{-10pt} f\left( a\right) \qquad \quad f^{+}\left( v\right) \colonequals \hspace{-8pt} \sum_{\substack{a\in A;\\[2pt] a \text{ の始点は } v}} \hspace{-10pt} f\left( a\right) \]\(f^{-}\left( v\right) \) を \(f\) における \(v\) への入流量 (inflow) と呼び、\(f^{+}\left( v\right) \) を \(f\) における \(v\) からの出流量 (outflow) と呼ぶ。
-
値 \(f^{+}\left( s\right) -f^{-}\left( s\right) \) を写像 \(f\) の値 (value) と定義し、\(\left\vert f\right\vert \) と表記する。
例 9.1.7 のフロー \(f\) は次の等式を満たす:
また、\(f\) の値は \(3\) であり、\(\left\vert f\right\vert =3\) が成り立つ。例 9.1.7 のフロー \(g\) では \(\left\vert g\right\vert =1\) となる。より一般的に言うと、Remark 9.1.8 のように定めたフロー \(f_{\mathbf{p}}\) は常に \(\left\vert f_{\mathbf{p}}\right\vert =1\) を満たす。
任意のネットワーク \(N\) に対して、\(N\) 上の零フロー (zero flow) を定義できる。このフロー \(0_{A}\colon A\rightarrow\mathbb{N}\) は任意の弧 \(a \in A\) を \(0\) に移す写像である。このフローの値は \(0\) である。