9.4. 最大フロー最小カット定理
9.4.1 カットの定義
メインディッシュの前に、もう一つ概念を定義する:
多重有向グラフ \(D=\left( V,A,\psi\right) \)、入口 \(s \in V\)、出口 \(t \in V\)、容量関数 \(c\colon A\rightarrow\mathbb{N}\) から構成されるネットワークを \(N\) とする。このとき:
-
\(N\) のカット (cut) とは、\(\left[ S,\overline{S}\right] \) の形をした \(A\) の部分集合を意味する。ここで \(S\) は \(V\) の部分集合であり、\(s\in S\) と \(t\notin S\) を満たす。
-
カット \(\left[ S,\overline {S}\right] \) の容量 (capacity) は、値 \(c\left( S,\overline{S}\right) =\sum\limits_{a\in\left[ S,\overline{S}\right] }c\left( a\right) \) と定義される。
例 9.1.2 のネットワークをもう一度考える。集合 \(\left[ \left\{ s,u\right\},\, \overline{\left\{ s,u\right\} }\right] =\left\{ sp,\ uv,\ uq\right\} \) は、このネットワークのカットである。このカットの容量は \(c\left( \left\{ s,u\right\},\, \overline{\left\{ s,u\right\} }\right) =5\) である。
9.4.2 最大フロー最小カット定理: 主張
命題 9.3.2 (c) からは、任意のフローの値は任意のカット \(\left[ S,\overline{S}\right] \) の容量より大きくならないと分かる。
さらに、命題 9.3.2 (d) によれば、この不等式が等号となる ── フロー \(f\) の値が何らかのカット \(\left[ S,\overline{S}\right] \) の容量と等しい ── のは、フロー \(f\) がそのカットを順方向 (\(S\) から \(\overline{S}\) に向かう方向) に容量を使い切りつつ横切り、逆方向 (\(\overline{S}\) から \(S\) に向かう方向) には横切らないとき、かつそのときに限る。
この不等式は任意の最大フローと任意の最小カットに対して等式となる:
多重有向グラフ \(D=\left( V,A,\psi\right) \)、入口 \(s \in V\)、出口 \(t \in V\)、容量関数 \(c\colon A\rightarrow\mathbb{N}\) から構成されるネットワークを \(N\) とする。このとき次の等式が成り立つ:
この証明の概略を本節の最後に示す。その証明は、最大フロー (値が最大のフロー) と最小カット (容量が最小のカット) を実際に求めるアルゴリズムの説明でもある。これは Ford-Fulkerson のアルゴリズムと呼ばれるそれなりに効率的な (多項式時間の) アルゴリズムであり、現実世界の問題を解くのに十分な速度を持つ。
9.4.3 フローの増加
Ford-Fulkerson のアルゴリズムは、最初に \(f\) を零フロー (例 9.1.11) として、弧流量 \(f\left( a\right) \) の一部を変更して \(\left\vert f\right\vert \) を増加させる操作を何度も繰り返すことで動作する。
当然、一つの弧の弧流量 \(f\left( a\right) \) だけを変えるとフローの保存制約が満たされなくなるので、変更後の写像をフローとするには \(f\left( a\right) \) を変えたときに他の弧 \(b \in A\) に対する \(f\left( b\right) \) にも変更が必要になる。この変更を正しく行う方法の一つとして、\(s\) から \(t\) への路に沿って弧流量 \(f\left( a\right) \) を増加させるというものがある。この方法でフローの値を増加させる例を示す:
例 9.1.7 のフロー \(f\) を考える。\(s\) から \(t\) への路 \(\left( s,p,q,v,t\right) \) に含まれる全ての弧は容量に空きがあるので、\(f\) の弧流量 \(f\left( sp\right)\), \(f\left( pq\right)\), \(f\left( qv\right)\), \(f\left( vt\right) \) を増加させることができる。これらの弧流量を増加させると次のフローが得られる:
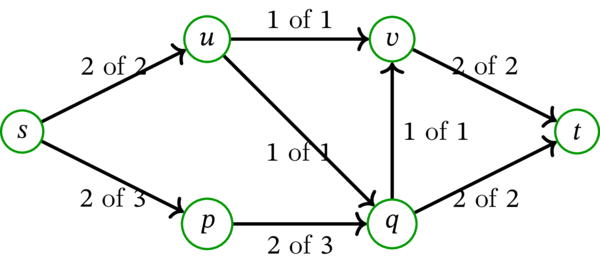
このフローの値は \(4\) である。これが最大フローであることは容易に分かる。実際、値 \(4\) はカット \(\left[ \overline{\left\{ t\right\} },\left\{ t\right\} \right] \) の容量 \(c\left( \overline{\left\{ t\right\} },\left\{ t\right\} \right) \) に等しく、命題 9.3.2 (c) より任意のフローの値は任意のカットの容量より大きくならない。
ただし、この例のようにネットワークを構成するグラフの路に沿ってフローの値を増加させる単純な操作を繰り返すだけで必ず最大フローが得られるとは限らない。この操作は極大値で行き詰まる可能性がある ── つまり、フローの改善に利用できる \(s\) から \(t\) への路 (容量に空きがある弧だけを持つ \(s\) から \(t\) への路) が存在しないにもかかわらず、そのフローが最大フローでない状況があり得る。この状況の例を次に示す:
次のネットワークとフローを考える:
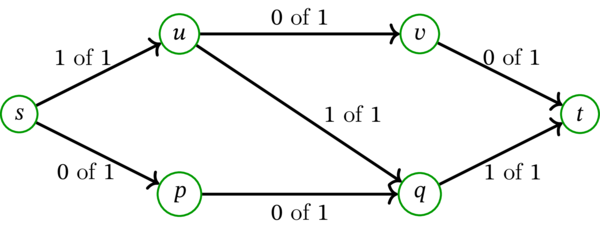
このフローは明らかに最大フローでないものの、\(s\) から \(t\) への任意の路は容量に空きがない弧を少なくとも一つ含む。つまり \(s\) から \(t\) への路に含まれる弧の弧流量を増加させることでこのフローを改善することはできない。
この問題は「ジグザグ路」を考えると回避できる ── ジグザグ路は厳密な意味での路ではなく、弧を順方向にも逆方向にも使う頂点と弧の列 \(\left( v_{0},a_{1},v_{1},a_{2},v_{2},\ldots,a_{k},v_{k}\right) \) を意味する (任意の \(i\in\left\{ 1,2,\ldots,k\right\} \) は \(\psi\left( a_{i}\right) =\left( v_{i-1},v_{i}\right) \) または \(\psi\left( a_{i}\right) =\left( v_{i},v_{i-1}\right) \) を満たす)。ジグザグ路を使ってフローの値を増加させるときは少し手の込んだ処理が必要になる: 含まれる弧の弧流量を全て増加させるのではなく、順方向の弧では弧流量を増やし、逆方向の弧では弧流量を減らす必要がある。こうしたときフローの保存制約は満たされたままとなる (理由を考えてみてほしい。厳密な証明は後で示す) ので、これはフローの値を増加させる正当な操作である。この操作の例を示す:
例 9.4.5 のネットワークとフローを考える。このネットワークを構成する有向グラフはジグザグ路 \(\left( s, sp, p, pq, q, qu, u, uv, v, vt, t\right) \) を持つ。このジグザグ路では弧 \(uq\) だけが逆方向に使われている。このジグザグ路の順方向の弧 \(sp\), \(pq\), \(uv\), \(vt\) の弧流量を \(1\) だけ増やし、逆方向の弧 \(uq\) の弧流量を \(1\) だけ減らせば、次の改善されたフローが得られる:
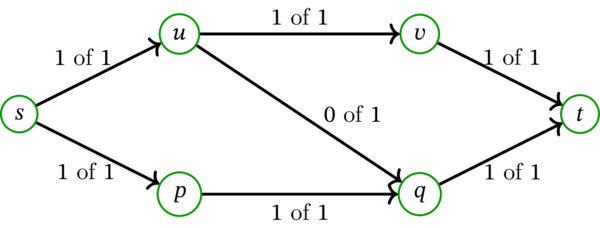
この新しいフローは値が \(2\) であり、これが最大フローであることは簡単に確かめられる。
良いニュース: このように「ジグザグ路」の利用を許すなら、通常の路だけを考える場合とは異なり、最大でないフローで行き詰まることはない。最大フローが得られるまでフローの値を大きくし続けることが必ずできる。
この事実を証明するために、いくつか用語を導入する。本書では「ジグザグ路」という概念は定義せず、適切に構築された (\(D\) と異なる) 有向グラフにおける通常の路を「ジグザグ路」と解釈する。こうすると路の様々な性質を「ジグザグ路」に一般化しないで済む。
9.4.4 残余有向グラフ
その「適切に構築されたグラフ」は残余有向グラフと呼ばれ、次のように定義される:
多重有向グラフ \(D=\left( V,A,\psi\right) \)、入口 \(s \in V\)、出口 \(t \in V\)、容量関数 \(c\colon A\rightarrow\mathbb{N}\) から構成されるネットワークを \(N\) とする。
-
任意の弧 \(a \in A\) に対して、\(a\) の反転として振る舞う新しい弧を \(a^{-1}\) と定義する (つまり \(a^{-1}\) の始点は \(a\) の終点に等しく、\(a^{-1}\) の終点は \(a\) の始点に等しい)。この新しい弧 \(a^{-1}\) を有向グラフ \(D\) に追加するわけではないものの、後で定義する有向グラフで利用する。
厳密に言うと次のようになる: それぞれの弧 \(a \in A\) に対して新しいオブジェクトを用意して、それを \(a^{-1}\) と呼ぶ。それぞれの弧 \(a \in A\) に対する \(a^{-1}\) を集めた集合を \(A^{-1}\) とする。さらに、写像 \(\psi\colon A\rightarrow V\times V\) を次のように拡張して \(\widehat{\psi}\colon A\cup A^{-1}\rightarrow V\times V\) を定義する:
\[ \widehat{\psi}\left( a\right) =\left( u,v\right), \qquad\quad \widehat{\psi}\left(a^{-1}\right) =\left( v,u\right) \]ここで \(u\) と \(v\) は \(\left( u,v\right) =\psi\left( a\right) \) を満たす頂点を表す。
任意の弧 \(a \in A\) に対応する新しい弧 \(a^{-1}\) を \(a\) の反転 (reversal) と呼ぶ。逆に、\(a^{-1}\) の反転を \(a\) と定義する。また、任意の弧 \(a \in A\) に対して \(\left( a^{-1}\right) ^{-1}\colonequals a\) と定める。
弧 \(a \in A\) を順方向弧 (forward arc) と呼び、\(a\) の反転 \(a^{-1}\) を逆方向弧 (backward arc) と呼ぶ。
-
\(f\colon A\rightarrow\mathbb{N}\) を \(N\) 上の任意のフローとする。このフロー \(f\) に関する残余有向グラフ (residual digraph) \(D_{f}\) を多重有向グラフ \(\left( V,A_{f},\psi_{f}\right) \) と定める。ここで \(A_{f}\) と \(\psi_{f}\) は次のように定義される:
\[ \begin{aligned} A_{f} &\colonequals \left\{ a\in A\mid f\left( a\right) < c\left( a\right) \right\} \cup \left\{ a^{-1}\mid a\in A\ \wedge \ f\left( a\right) >0\right\} \\ \psi_{f} &\colonequals \widehat{\psi}|_{A_{f}} \end{aligned} \]つまり、残余有向グラフ \(D_{f}\) の頂点集合は \(D\) の頂点集合と等しく、弧集合は \(f\) が容量を使い切っていない弧と、\(f\) が利用する弧の反転から構成される。
例 9.1.7 で考えたフロー \(f\) に関する残余有向グラフ \(D_{f}\) を次に示す:
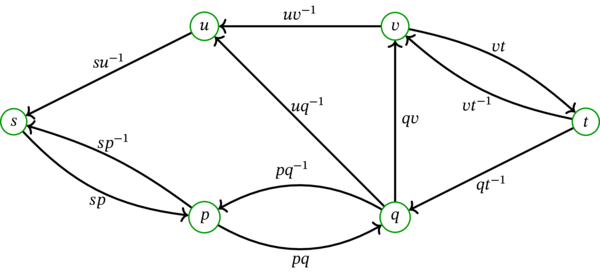
\(D\) は閉路を持たないのに対して、\(D_{f}\) は閉路を持つことに注意せよ!
例 9.4.5 で考えた最大でないフローを \(f\) とする。\(f\) に関する有向残余グラフ \(D_{f}\) を次に示す:
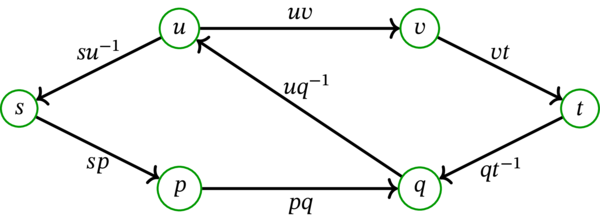
この有向グラフ \(D_{f}\) は \(s\) から \(t\) への路を持ち、それは例 9.4.6 で考えた「ジグザグ路」 \(\left( s,p,q,u,v,t\right) \) にちょうど対応する。
残余有向グラフ \(D_{f}\) の弧は変更可能な弧流量を表すと解釈できる。具体的に言えば、\(D_{f}\) の順方向弧 \(a\) は \(f\left( a\right) \) を増やせることを表し、\(D_{f}\) の逆方向弧 \(a^{-1}\) は \(f\left( a\right) \) を減らせることを表す。つまり、残余有向グラフ \(D_{f}\) における路は \(D\) の「ジグザグ路」であり、例 9.4.6 で見たように \(f\) の弧流量を増減させて値を増加させるために利用できる。さらに、残余有向グラフ \(D_{f}\) を使えば「ジグザグ路」という新しい概念を考える必要はない。
9.4.5 増加路補題
次の非常に重要な補題は「ジグザグ路を使ったフローの改善」が正当である (フローをフローに変更する) こと、そして「ジグザグ路を使ったフローの改善」の反復が最大フローを見つける (最大フローは改善できない) ことを示す:
多重有向グラフ \(D=\left( V,A,\psi\right) \)、入口 \(s \in V\)、出口 \(t \in V\)、容量関数 \(c\colon A\rightarrow\mathbb{N}\) から構成されるネットワークを \(N\) とする。写像 \(f\colon A\rightarrow\mathbb{N}\) を \(N\) 上のフローとする。
-
残余有向グラフ \(D_{f}\) が \(s\) から \(t\) への路を持つなら、\(f\) より大きな値を持つ \(N\) 上のフロー \(f^{\prime}\) が存在する。
-
残余有向グラフ \(D_{f}\) が \(s\) から \(t\) への路を持たないとき、\(f\) の値は最大 (\(N\) 上のフローの中で最大) である。さらに、このとき \(V\) の部分集合 \(S\) で \(s\in S\) と \(t\notin S\) と \(\left\vert f\right\vert =c\left( S,\overline{S}\right) \) を満たすものが存在する。
(a): 残余有向グラフ \(D_{f}\) が \(s\) から \(t\) への路を持つと仮定する。そのような路を一つ取って \(\mathbf{p}\) とする。このとき \(\mathbf{p}\) の弧は全て \(D_{f}\) の弧である。
\(\mathbf{p}\) に含まれる任意の順方向弧 \(a\in A\) に注目すると、\(a\) は \(D_{f}\) の弧より \(f\left( a\right) < c\left( a\right) \) が成り立つから、フローの容量制約を破ることなく何らかの正整数 \(\varepsilon\in\mathbb{N}\) だけ弧流量 \(f\left( a\right) \) を大きくできると分かる1 (具体的には \(\varepsilon \leq c\left( a\right) -f\left( a\right) \) を満たす任意の \(\varepsilon\) だけ大きくできる)。
\(\mathbf{p}\) に含まれる任意の逆方向弧 \(a^{-1}\in A^{-1}\) に注目すると、\(a^{-1}\) は \(D_{f}\) の弧より \(f\left( a\right) > 0\) が成り立つから、フローの容量制約を破ることなく何らかの正整数 \(\varepsilon \in\mathbb{N}\) だけ弧流量 \(f\left( a\right) \) を小さくできると分かる (具体的には \(\varepsilon \leq f\left( a\right) \) を満たす任意の \(\varepsilon\) だけ小さくできる)。
\(\varepsilon\) を次のように定める:
\(\varepsilon\) は正整数だけから構成される集合2の最小値なので、正整数である。
\(f\) を次のように改変して得られる写像を \(f^{\prime}\colon A\rightarrow\mathbb{N}\) とする:
-
\(\mathbf{p}\) に含まれる順方向弧 \(a \in A\) ごとに弧流量 \(f\left( a\right) \) を \(\varepsilon\) だけ増加させる (つまり \(f^{\prime}\left( a\right) \colonequals f\left( a\right) +\varepsilon\) と定める)。
-
\(\mathbf{p}\) に含まれる逆方向弧 \(a^{-1}\in A^{-1}\) ごとに弧流量 \(f\left( a\right) \) を \(\varepsilon\) だけ減少させる (つまり \(f^{\prime}\left( a\right) \colonequals f\left( a\right) -\varepsilon\) と定める)。
-
それ以外の \(D\) の弧 \(a\) の弧流量 \(f\left( a\right) \) はそのままとする (つまり \(f^{\prime}\left( a\right) \colonequals f\left( a\right) \) と定める)。
この新しい写像 \(f^{\prime}\) は明らかにフローの容量制約を満たす3。これから \(f^{\prime}\) がフローの保存制約も満たすことを示す。このためには、任意の頂点 \(v\in V\setminus\left\{ s,t\right\} \) が \(\left( f^{\prime}\right) ^{-}\left( v\right) =\left( f^{\prime}\right) ^{+}\left( v\right) \) を満たすことを証明する必要がある。
頂点 \(v\in V\setminus\left\{ s,t\right\} \) を任意に取る。\(f\) はフローより \(f^{-}\left( v\right) =f^{+}\left( v\right) \) が分かる。これを使って \(\left( f^{\prime}\right) ^{-}\left( v\right) =\left( f^{\prime}\right) ^{+}\left( v\right) \) を示せばよい。
路 \(\mathbf{p}\) は \(s\) から \(t\) への路だから、\(v\in V\setminus\left\{ s,t\right\} \) は \(\mathbf{p}\) の始点でも終点でもない。よって \(v\) が路 \(\mathbf{p}\) に含まれるなら、路 \(\mathbf{p}\) は何らかの弧を通じて \(v\) に到達し、別の何らかの弧を通じて \(v\) を離れる。従って次のいずれかが成り立つ:
- Case 1: 頂点 \(v\) は路 \(\mathbf{p}\) に含まれない。
-
Case 2: \(\mathbf{p}\) は順方向弧を通じて \(v\) に到達し、順方向弧を通じて \(v\) から離れる。
-
Case 3: \(\mathbf{p}\) は順方向弧を通じて \(v\) に到達し、逆方向弧を通じて \(v\) から離れる。
-
Case 4: \(\mathbf{p}\) は逆方向弧を通じて \(v\) に到達し、順方向弧を通じて \(v\) から離れる。
-
Case 5: \(\mathbf{p}\) は逆方向弧を通じて \(v\) に到達し、逆方向弧を通じて \(v\) から離れる。
この五つの場合のそれぞれで \(\left( f^{\prime}\right) ^{-}\left( v\right) =\left( f^{\prime}\right) ^{+}\left( v\right) \) を証明すればよい。最初の三つの場合に対する証明を示す:
Case 1 を考える。頂点 \(v\) は \(\mathbf{p}\) に含まれないから、\(v\) を終点に持つ任意の弧 \(a\in A\) は \(f^{\prime }\left( a\right) =f\left( a\right) \) を満たす (\(a\) と \(a^{-1}\) がどちらも \(\mathbf{p}\) に含まれないため)。よって \(\left( f^{\prime}\right) ^{-}\left( v\right) =f^{-}\left( v\right) \) を得る。同様に \(\left( f^{\prime}\right) ^{+}\left( v\right) =f^{+}\left( v\right) \) も分かる。つまり \(\left( f^{\prime }\right) ^{-}\left( v\right) =f^{-}\left( v\right) =f^{+}\left( v\right) =\left( f^{\prime}\right) ^{+}\left( v\right) \) であり、Case 1 で \(\left( f^{\prime}\right) ^{-}\left( v\right) =\left( f^{\prime }\right) ^{+}\left( v\right) \) は証明された。
Case 2 を考える。路 \(\mathbf{p}\) が順方向弧 \(b\) を通じて \(v\) に到達し、順方向弧 \(c\) を通じて \(v\) から離れるとする。\(b\) と \(c\) は \(D\) の弧であり、\(v\) は \(b\) の終点かつ \(c\) の始点である。\(f^{\prime}\) の定義より \(f^{\prime}\left( b\right) =f\left( b\right) +\varepsilon\) であり、\(v\) を終点とする \(b\) 以外の弧 \(a \in A\) では \(f^{\prime}\left( a\right) =f\left( a\right) \) が成り立つ。ここから \(\left( f^{\prime}\right) ^{-}\left( v\right) =f^{-}\left( v\right) +\varepsilon\) を得る。同様に、弧 \(c\) に注目すれば \(\left( f^{\prime}\right) ^{+}\left( v\right) =f^{+}\left( v\right) +\varepsilon\) が分かる。つまり \(\left( f^{\prime}\right) ^{-}\left( v\right) =f^{-}\left( v\right) + \varepsilon=f^{+}\left( v\right) +\varepsilon=\left( f^{\prime}\right) ^{+}\left( v\right) \) であり、Case 2 で \(\left( f^{\prime}\right) ^{-}\left( v\right) =\left( f^{\prime}\right) ^{+}\left( v\right) \) は証明された。
Case 3 を考える。路 \(\mathbf{p}\) が順方向弧 \(b\) を通じて \(v\) に到達し、逆方向弧 \(c^{-1}\) を通じて \(v\) から離れるとする。\(b\) と \(c\) は \(D\) の弧であり、\(v\) は \(b\) の終点かつ \(c\) の終点である。\(f^{\prime}\) の定義より \(\mathbf{p}\) は順方向弧 \(b\) を含むので \(f^{\prime}\left( b\right) =f\left( b\right) +\varepsilon\) であり、\(\mathbf{p}\) は逆方向弧 \(c^{-1}\) を含むので \(f^{\prime}\left( c\right) =f\left( c\right) -\varepsilon\) であり、\(v\) を終点とする \(b\) と \(c\) 以外の弧 \(a \in V\) では \(f^{\prime}\left( a\right) =f\left( a\right) \) だと分かる。ここから \(\left( f^{\prime }\right) ^{-}\left( v\right) =f^{-}\left( v\right) +\varepsilon -\varepsilon=f^{-}\left( v\right) \) を得る。また、\(v\) を始点とする \(D\) の任意の弧およびその反転は \(\mathbf{p}\) に含まれないので \(\left( f^{\prime}\right) ^{+}\left( v\right) =f^{+}\left( v\right) \) が成り立つ。つまり \(\left( f^{\prime}\right) ^{-}\left( v\right) =f^{-}\left( v\right) =f^{+}\left( v\right) =\left( f^{\prime}\right) ^{+}\left( v\right) \) であり、Case 3 で \(\left( f^{\prime}\right) ^{-}\left( v\right) =\left( f^{\prime}\right) ^{+}\left( v\right) \) は証明された。
他の二つの場合も同じように示せる (Case 4 は Case 3 と似た議論、Case 5 は Case 2 と似た議論となる)。よって \(\left( f^{\prime }\right) ^{-}\left( v\right) =\left( f^{\prime}\right) ^{+}\left( v\right) \) は五つの場合のそれぞれで証明された。
\(v\) を固定したことを忘れる。以上で任意の頂点 \(v\in V\setminus\left\{ s,t\right\} \) が \(\left( f^{\prime}\right) ^{-}\left( v\right) =\left( f^{\prime}\right) ^{+}\left( v\right) \) を満たすことが証明された。言い換えれば、写像 \(f^{\prime}\) はフローの保存制約を満たす。先述したように \(f^{\prime}\) はフローの容量制約も満たすから、\(f^{\prime}\) はフローだと結論できる。
続いて、このフローの値 \(\left\vert f^{\prime}\right\vert \) を求める。路 \(\mathbf{p}\) の始点が \(s\) なので、\(\mathbf{p}\) は何らかの弧 \(\gamma\) を通じて \(s\) を離れ、その後 \(s\) に戻らない (\(s \neq t\) より \(\mathbf{p}\) は少なくとも一つの弧を持つ)。この弧 \(\gamma\) が順方向弧 \(b\) なら \(f^{\prime}\left( b\right) =f\left( b\right) +\varepsilon\) であり、ここから \(\left( f^{\prime}\right) ^{+}\left( s\right) =f^{+}\left( s\right) +\varepsilon\) と \(\left( f^{\prime }\right) ^{-}\left( s\right) =f^{-}\left( s\right) \) を得る。もし弧 \(\gamma\) が逆方向弧 \(c^{-1}\) なら \(f^{\prime}\left( c\right) =f\left( c\right) -\varepsilon\) であり、ここから \(\left( f^{\prime}\right) ^{-}\left( s\right) =f^{-}\left( s\right) -\varepsilon\) と \(\left( f^{\prime}\right) ^{+}\left( s\right) =f^{+}\left( s\right) \) を得る。よって次の等式が分かる:
よって、フローの値の定義より次を得る:
言い換えれば、フロー \(f^{\prime}\) は \(f\) より大きな値を持つ。\(f\) より大きな値を持つフローが見つかったので、補題 9.4.10 (a) は証明された。
(b): 有向グラフ \(D_{f}\) が \(s\) から \(t\) への路を持たないと仮定する。\(V\) の部分集合 \(S\) を次のように定める:
自明な路 \(\left( s\right) \) が \(s\) から \(s\) への路なので \(s \in S\) が分かり、\(D_{f}\) は \(s\) から \(t\) への路を持たないと仮定しているので \(t \in S\) が分かる。これから \(\left\vert f\right\vert =c\left( S,\overline{S}\right) \) を証明する。
この証明には命題 9.3.2 (d) を用いる。このために、次の二つの命題を示す:
-
任意の \(a\in\left[ \overline{S}, S\right]\) に対して \(f\left( a\right) = 0\)
-
任意の \(a\in\left[ S,\overline{S}\right]\) に対して \(f\left( a\right) =c\left( a\right)\)
[(a) の証明: 背理法で示す。ある \(a\in\left[ \overline{S},S\right] \) で \(f\left( a\right) \neq0\) だと仮定する。フローの容量制約より \(f\left( a\right) \geq0\) だから、\(f\left( a\right) \neq0\) は \(f\left( a\right) >0\) を意味する。よって逆方向弧 \(a^{-1}\) は残余有向グラフ \(D_{f}\) の弧である。\(u\) を \(a\) の始点、\(v\) を \(a\) の終点とする。\(a\in\left[ \overline{S},S\right] \) より \(u \in \overline{S}\) と \(v \in S\) が分かる。\(v \in S\) なので、\(S\) の定義より有向グラフ \(D_{f}\) には \(s\) から \(v\) への路が存在する。この路を \(\mathbf{q}\) とする。逆方向弧 \(a^{-1}\) (始点 \(v\) と終点 \(u\) を持つ弧) と頂点 \(u\) を \(\mathbf{q}\) の末尾に付け足すと、\(D_{f}\) における \(s\) から \(u\) への歩道が得られる。\(D_{f}\) は \(s\) から \(u\) への歩道を持つので、命題 4.5.8 より \(D_{f}\) は \(s\) から \(u\) への路を持つ。ここから \(S\) の定義より \(u \in S\) を得る。しかし、これは \(u\in\overline{S}=V\setminus S\) と矛盾する。この矛盾から仮定 \(f\left( a\right) \neq0\) が偽だと分かる。つまり \(f\left( a\right) =0\) である。]
[(b) の証明: 背理法で示す。ある \(a\in\left[ S,\overline{S}\right] \) で \(f\left( a\right) \neq c\left( a\right) \) だと仮定する。フローの容量制約より \(f\left( a\right) \leq c\left( a\right) \) だから、\(f\left( a\right) \neq c\left( a\right) \) は \(f\left( a\right) < c\left( a\right) \) を意味する。よって順方向弧 \(a\) は残余有向グラフ \(D_{f}\) の弧である。\(u\) を \(a\) の始点、\(v\) を \(a\) の終点とする。\(a\in\left[ S,\overline{S}\right] \) より \(u \in S\) と \(v \in \overline{S}\) が分かる。\(u \in S\) なので、\(S\) の定義より有向グラフ \(D_{f}\) には \(s\) から \(u\) への路が存在する。この路を \(\mathbf{q}\) とする。順方向弧 \(a\) (始点 \(u\) と終点 \(v\) を持つ弧) と頂点 \(v\) を \(\mathbf{q}\) の末尾に付け足すと、\(D_{f}\) における \(s\) から \(v\) への歩道が得られる。\(D_{f}\) は \(s\) から \(v\) への歩道を持つので、命題 4.5.8 より \(D_{f}\) は \(s\) から \(v\) への路を持つ。ここから \(S\) の定義より \(v \in S\) を得る。しかし、これは \(v \in\overline{S}=V\setminus S\) と矛盾する。この矛盾から仮定 \(f\left( a\right) \neq c\left( a\right) \) が偽だと分かる。つまり \(f\left( a\right) =c\left( a\right) \) である。]
よって命題 9.3.2 (d) より \(\left\vert f\right\vert =c\left( S,\overline{S}\right) \) が成り立つ。
これで \(s\in S\) と \(t\notin S\) と \(\left\vert f\right\vert =c\left( S,\overline{S}\right) \) を満たす \(V\) の部分集合 \(S\) が見つかった。補題 9.4.10 (b) を証明するには、これに加えてフロー \(f\) が (\(N\) 上のフローの中で) 最大の値を持つと示す必要がある。ただ、これは易しい: 命題 9.3.2 (c) より、\(N\) 上の任意のフロー \(g\) の値は \(\left\vert g\right\vert \leq c\left( S,\overline{S}\right) \) を満たす。\(\left\vert f\right\vert =c\left( S,\overline{S}\right) \) だから、\(N\) 上の任意のフロー \(g\) に対して \(\left\vert g\right\vert \leq\left\vert f\right\vert \) が成り立つ。つまりフロー \(f\) は最大の値を持つ。以上で補題 9.4.10 (b) は証明された。□
9.4.6 最大フロー最小カット定理の証明
これで最大フロー最小カット定理 (定理 9.4.3) を証明する準備が整った。
\(f\colon A\rightarrow\mathbb{N}\) を \(N\) 上の零フローとする (零フローは例 9.1.11 で定義した)。続いて、次のアルゴリズム (Ford-Fulkerson のアルゴリズムと呼ばれる) を使ってフロー \(f\) の値 \(\left\vert f\right\vert \) を段階的に大きくすることを考える:
-
残余有向グラフ \(D_{f}\) を構築する。
-
有向グラフ \(D_{f}\) が \(s\) から \(t\) への路を持つなら、補題 9.4.10 (a) よりネットワーク \(N\) は \(f\) より値が大きいフロー \(f^{\prime}\) を持つ (さらに、補題 9.4.10 (a) の証明からは \(f^{\prime}\) を効率的に求める方法4が分かる)。そのような \(f^{\prime}\) を一つ取り、それを \(f\) としてステップ 1 に進む。
-
\(D_{f}\) が \(s\) から \(t\) への路を持たないなら、\(f\) を出力して終了する。
\(f\) を \(f^{\prime}\) に置き換えるステップ 2 の操作をフローの増加 (augmentation) と呼ぶ。つまり、このアルゴリズムは増加を可能な限り繰り返すことで動作する。
このアルゴリズムがいずれ終了する (フローの増加を繰り返すと、いずれフローの増加が不可能になる) ことを示す。フロー \(f\) を増加させると値 \(\left\vert f\right\vert \) が大きくなる。\(\left\vert f\right\vert \) は整数なので、\(\left\vert f\right\vert \) は \(f\) の増加ごとに \(1\) 以上大きくなる。一方、\(\left\vert f\right\vert \) は任意のカット \(\left[ S,\overline{S}\right] \) の容量 \(c\left( S,\overline{S}\right) \) より大きくならない (命題 9.3.2 (c) より)。\(f\) の初期値である零フローの値は \(0\) なので、フローの値を \(1\) 以上大きくする操作は最大でも \(c\left( S,\overline{S}\right) \) 回しか行えない。つまりフローの増加は連続で最大でも \(c\left( S,\overline{S}\right) \) 回しか行えない。
よって上述のアルゴリズムはいずれ終了する。このアルゴリズムが出力するフローを \(f\) とする。このフロー \(f\) は「残余有向グラフ \(D_{f}\) が \(s\) から \(t\) への路を持たない」という条件を満たす。よって補題 9.4.10 (b) より、フロー \(f\) は \(N\) 上のフローの中で最大の値を持ち、\(s\in S\) と \(t\notin S\) と \(\left\vert f\right\vert =c\left( S,\overline{S}\right) \) を満たす \(V\) の部分集合 \(S\) が存在する。この \(S\) に注目する。
フロー \(f\) の値が最大なので、次の等式が成り立つ:
一方で命題 9.3.2 (c) より、\(s\in T\) と \(t\notin T\) を満たす \(V\) の任意の部分集合 \(T\) に対して次の等式が成り立つ:
ここから次の等式を得る:
一方で次の等式も成り立つ:
二つの等式を比較すれば次を得る:
言い換えれば、フローの値の最大値はカットの容量の最小値に等しい。以上で定理 9.4.3 は証明された。 □
本章で示した全ての定理、命題、補題は集合 \(\mathbb{N}\) を集合 \(\mathbb{Q}_{+}\colonequals \left\{ \text{非負有理数}\right\} \) または \(\mathbb{R}_{+}\colonequals \left\{ \text{非負実数}\right\} \) に置き換えたとしても成り立つ。ただし、そうすると証明は複雑になる。問題となるのは、弧流量が \(\mathbb{N}\) ではなく \(\mathbb{Q}_{+}\) または \(\mathbb{R}_{+}\) に属するとき、\(\left\vert f\right\vert \) の増加が必ず有限回で止まる保証が無い事実である (参考: アルキメデスと亀に関するゼノンのパラドックス)。つまり、フローの値の改善が小さくなり続けて最大値に達しない可能性がある (それどころか、フローの値が最大値に近づきさえしない可能性もある!)。
弧流量が有理数のとき、この状況は幸い発生しない: 全ての弧流量 \(f\left( a\right) \) を通分したものを考えると、フローを増加させても分母が変化しないことが分かる。 しかし弧流量が非負実数のケースでは、この望ましくない振る舞いが発生する可能性が否定できない ([ForFul74, § I.8] に例が載っている)。幸い、この振る舞いは \(D_{f}\) における \(s\) から \(t\) への最短路を選択することで回避できる。このアルゴリズムは Edmonds-Karp バージョンの Ford-Fulkerson アルゴリズムまたは Edmonds-Karp のアルゴリズム (Edmonds-Karp algorithm) と呼ばれる。この事実の証明には少し手間がかかるので、本書では示さない (例えば [Schrij17, Theorem 4.4] を見てほしい)。ちなみに、このテクニックは整数値のフローに対しても高速である (実行時間が \(O( \left\vert V\right\vert \cdot\left\vert A\right\vert ^{2}) \) である) ことが保証されている。
-
もちろん、弧流量を一つだけ変更するとフローの保存制約が満たされなくなる。 ↩︎
-
なぜなら:
-
\(\mathbf{p}\) に含まれる任意の順方向弧 \(a \in A\) に対しては \(f\left( a\right) < c\left( a\right) \) つまり \(c\left( a\right) -f\left( a\right) >0\) が成り立つ。
-
\(\mathbf{p}\) に含まれる任意の逆方向弧 \(a^{-1}\in A^{-1}\) に対しては \(f\left( a\right) >0\) が成り立つ。
-
-
\(\varepsilon\) の定義より次が分かる:
-
\(\mathbf{p}\) に含まれる任意の順方向弧 \(a \in A\) に対しては \(\varepsilon\leq c\left( a\right) -f\left( a\right) \) つまり \(f\left( a\right) +\varepsilon\leq c\left( a\right) \) が成り立つ。
-
\(\mathbf{p}\) に含まれる任意の逆方向弧 \(a^{-1}\in A^{-1}\) に対しては \(\varepsilon\leq f\left( a\right) \) つまり \(f\left( a\right) -\varepsilon\geq0\) が成り立つ。
-
-
\(D_{f}\) が持つ \(s\) から \(t\) への路を見つけるアルゴリズムが必要になるものの、このための効率的なアルゴリズムは多く知られている (例えば homework set #4 exercise 5 などを参照してほしい)。 ↩︎