9.2. 最大フロー問題と二部グラフ
フローに関する重要な最適化問題の一つに最大フロー問題 (maximum flow problem) 問題がある。これは与えられたネットワーク上のフローの中で値が最大のものを見つける問題である。
二部グラフの最大マッチングを見つける問題は最大フロー問題の特殊ケースである。
実際、\(\left( G,X,Y\right) \) を二部グラフとする。このグラフを次のように変形してネットワーク \(N\) を構築する:
-
新しい頂点 \(s\) と \(t\) を加える。
-
\(G\) の各辺 \(e\) を弧 \(\overrightarrow{e}\) に置き換える。\(\overrightarrow{e}\) の始点は \(X\) に属する \(e\) の端点で、終点は \(Y\) に属する \(e\) の端点とする。
-
\(s\) から \(X\) に属する各頂点への弧を加える。
-
\(Y\) に属する各頂点から \(t\) への弧を加える。
-
全ての弧に \(1\) の容量を割り当てる。
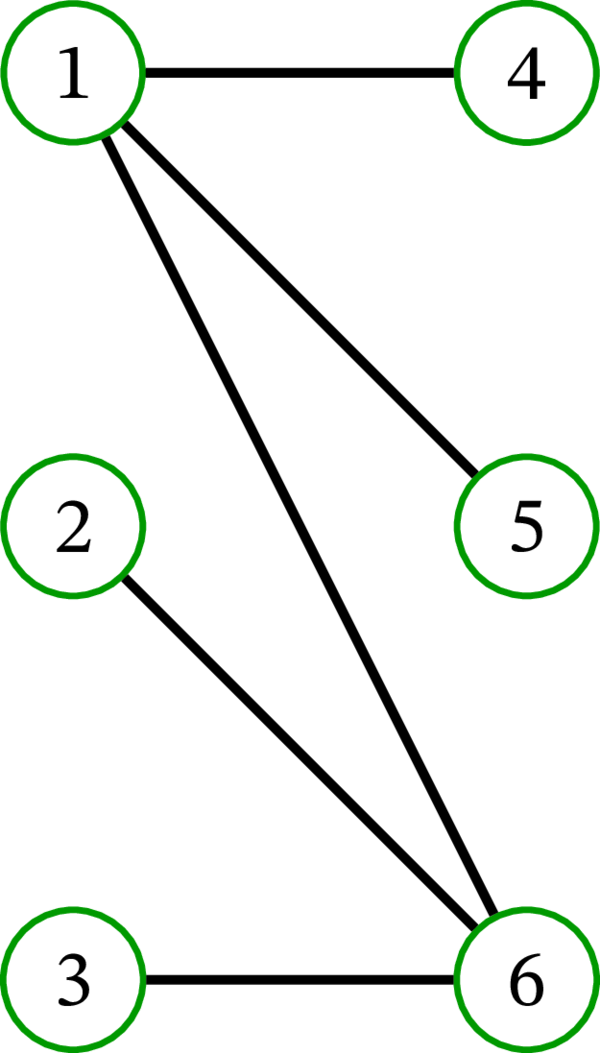
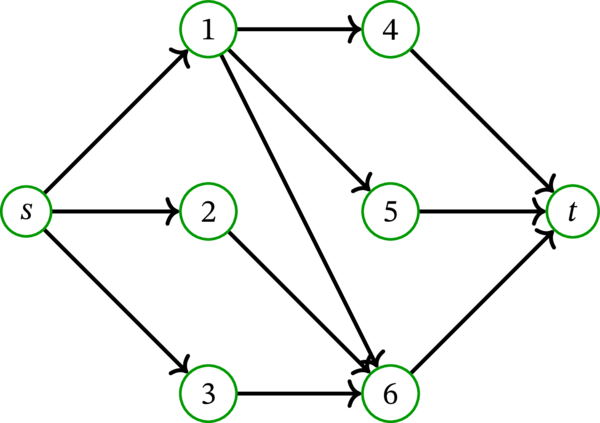
二部グラフ \(\left( G,X,Y\right) \) と、それに対応するネットワーク \(N\) の例を次に示す。以前と同じように、二部グラフの描画では \(X\) を左側に、\(Y\) を右側に書いている:
このネットワーク \(N\) 上のフローと \(G\) のマッチングの間には全単射が存在する。具体的には、\(N\) 上のフローを \(f\) とするとき、次の集合が \(G\) のマッチングとなる:
逆に、\(G\) のマッチング \(M\) からは次のように \(N\) 上のフローを構築できる: \(e\in M\) を使って \(\overrightarrow{e}\) と書ける弧に \(1\) の弧流量を割り当て、\(M\) でマッチ済みの頂点と \(s\) または \(t\) を結ぶ弧に \(1\) の弧流量を割り当て、その他の弧には \(0\) の弧流量を割り当てる。例えば、先ほどの例でマッチング \(\left\{ 15,\ 36\right\} \) は次のフローに対応する:
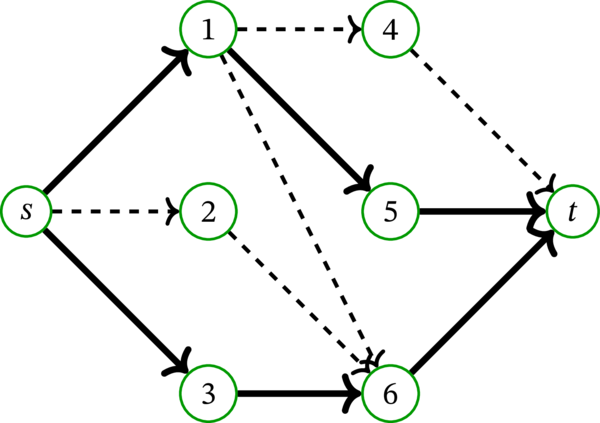
この図で破線は \(f\left( a\right) =0\) が成り立つ弧 \(a\) を表し、実線は \(f\left( a\right) = 1\) が成り立つ弧 \(a\) を表す (幸い、このフローでは弧の容量が \(0\) か \(1\) なので、破線と実線があればフローの容量を表現できる)。
この全単射の優れた性質として、フロー \(f\) とマッチング \(M\) が対応するとき \(\left\vert f\right\vert =\left\vert M\right\vert \) が成り立つことがある。そのため、値が最大のフローを見つける問題は要素数が最大のマッチングを見つける問題に等しい。