7.1. 独立集合の定義と Caro-Wei の定理

続いて、グラフ理論において最も基礎的な概念の一つを定義する:

定義 7.1.1

多重グラフ \(G\) の独立集合 (independent set) とは、\(\operatorname*{V}\left( G\right) \) の部分集合 \(S\) であって任意の二要素が \(G\) で隣接しないものを言う。

言い換えれば、\(G\) の独立集合は辺を持たない \(G\) の誘導部分グラフとほぼ等しい¹。なお、独立集合の定義にある「\(S\) の任意の二要素」は「\(S\) の任意の異なる二要素」ではない点に注意してほしい。

例えば、定義 2.3.2 で定義した「反三角形」は要素数 \(3\) の独立集合を意味する。

Remark 7.1.2

独立集合と適切な彩色には密接な関係がある: \(G\) をグラフ、\(k\) を自然数、\(f\colon V\rightarrow\left\{ 1,2,\ldots ,k\right\} \) を \(G\) の \(k\)-彩色とする。任意の \(i\in\left\{ 1,2,\ldots,k\right\} \) に対して、\(V_{i}\) を次のように定める:

\[ \begin{aligned} V_{i}\colonequals & \left\{ v\in V\mid f\left( v\right) =i\,\right\} \\ = & \left\{\text{色 } i \text{ を持つ } G \text{ の頂点}\right\} \end{aligned} \]

このとき、\(k\)-彩色 \(f\) が適切なのは、\(k\) 個の集合 \(V_{1},V_{2},\ldots,V_{k}\) が全て \(G\) の独立集合であるとき、かつそのときに限る。 [この事実は「独立集合」と「適切な \(k\)-彩色」の定義を展開すれば容易に示せる。]

グラフ理論における古典的な計算論的問題の一つとして、グラフが持つ最も大きな独立集合を見つける問題がある。この問題は NP 困難なので、高速に解くアルゴリズムが存在するとは思わない方がいい (独立集合の要素数の最大値を求めるアルゴリズムさえ望みは非常に薄い)。しかし、最大の独立集合の大きさには下界がいくつか知られている。その一つが次に示す Caro–Wei の定理 [AloSpe16, Chapter 6, Probabilistic Lens] である:

定理 7.1.3

[Caro–Wei の定理 (Caro–Wei theorem)] \(G=\left( V,E,\varphi \right) \) をループレスな多重グラフとする。このとき \(G\) は要素数が

\[ \sum_{v\in V}\dfrac{1}{1+\deg v} \]

以上の独立集合を持つ。

例 7.1.4

\(G\) を次のループレスな多重グラフとする:

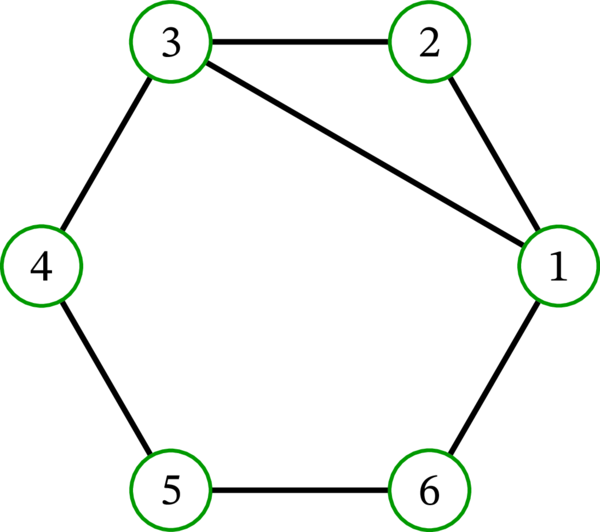
\(G\) の頂点の次数はそれぞれ \(3\), \(2\), \(3\), \(2\), \(2\), \(2\) だから、定理 7.1.3 より \(G\) には要素数が

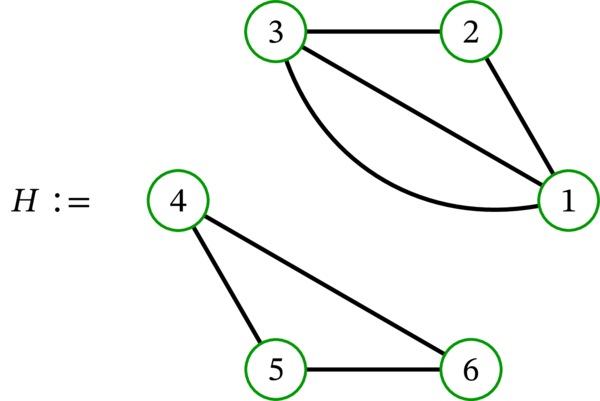
\[ \dfrac{1}{1+3}+\dfrac{1}{1+2}+\dfrac{1}{1+3}+\dfrac{1}{1+2}+\dfrac{1} {1+2}+\dfrac{1}{1+2}=\dfrac{11}{6}\approx1.83 \]

以上の独立集合が存在すると分かる。独立集合の要素数は整数だから、\(G\) は要素数が \(2\) 以上の独立集合が存在すると結論できる。なお実際には、\(G\) は要素数が \(3\) の独立集合 \(\left\{ 2,4,6\right\} \) を持つ。しかし、この事実を各頂点の次数から知る術はない。例えば次のグラフは各頂点の次数が \(G\) と等しいにもかかわらず、要素数が \(3\) の独立集合を持たない:

これから定理 7.1.3 の証明を二つ示す。どちらの証明でも有用なテクニックが利用される²。

[定理 7.1.3 の一つ目の証明] 背理法で示す。\(G\) の任意の独立集合が次の不等式を満たすと仮定する:

\[ \left\vert S\right\vert < \sum_{v\in V}\dfrac{1}{1+\deg v} \qquad (1) \]

\(V\) の要素を並べた列であって \(V\) の各要素をちょうど一度ずつ含むものを \(V\)-列挙 (\(V\)-listing) と呼ぶことにする。任意の \(V\)-列挙 \(\sigma\) に対して、\(V\) の部分集合 \(J_{\sigma}\) を次のように定める:

\[ J_{\sigma}\colonequals \left\{ v\in V \mid \sigma \text{ において } v \text{ が自身の\textbf{任意の}隣接頂点より前にある}\right\} \]

[例: \(G\) を次の多重グラフとする:

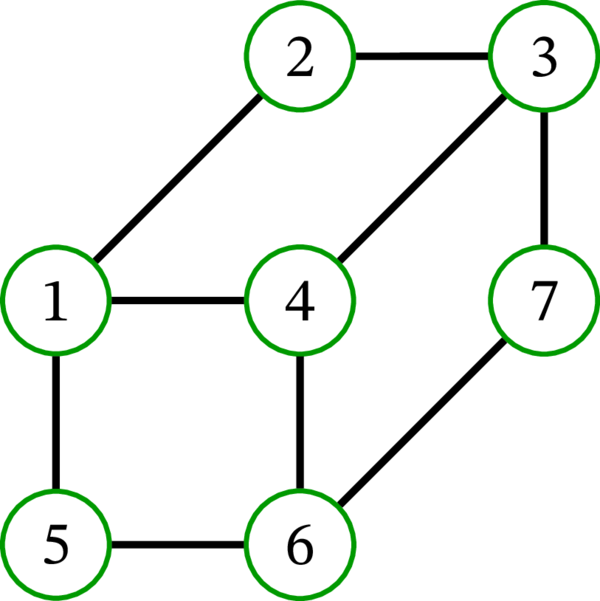
さらに \(\sigma\) を \(V\)-列挙 \(\left( 1,2,7,5,3,4,6\right) \) とする。このとき、頂点 \(1\) は \(\sigma\) において自身の隣接頂点 \(2\), \(4\), \(5\) より前にあるから、\(1\in J_{\sigma}\) が分かる。同様に、頂点 \(7\) は自身の隣接頂点 \(3\), \(6\) より前にあるから、\(7 \in J_{\sigma}\) も分かる。一方、頂点 \(2\) の隣接頂点 \(1\) は \(2\) より前にあるので、 \(2\notin J_{\sigma}\) が分かる。同様に頂点 \(5\), \(3\), \(4\), \(6\) はどれも \(J_{\sigma}\) に属さない。まとめると、この設定では \(J_{\sigma}=\left\{ 1,7\right\} \) である。]

集合 \(J_{\sigma}\) は \(G\) の独立集合である (仮に \(J_{\sigma}\) の任意の二要素 \(u\), \(v\) が隣接するなら、\(\sigma\) で \(u\) は \(v\) より前にあり、\(v\) は \(u\) より前にある。しかし、この二つの主張は明らかに矛盾する)。よって式 \((1)\) で \(S = J_{\sigma}\) とすれば次を得る:

\[ \left\vert J_{\sigma}\right\vert < \sum_{v\in V}\dfrac{1}{1+\deg v} \]

この不等式は任意の \(V\)-列挙 \(\sigma\) で成り立つ。よって、この不等式を全ての \(V\)-列挙にわたって足し上げれば次を得る:

\[ \begin{aligned} \sum_{\sigma:\, V \text{-列挙}}\left\vert J_{\sigma}\right\vert & < \sum_{\sigma:\, V \text{-列挙}}\ \ \sum_{v\in V}\dfrac{1}{1+\deg v} \\ & =\left(\text{\# } V \text{-列挙} \right) \cdot\sum_{v\in V}\dfrac{1}{1+\deg v} \qquad (2) \end{aligned} \]

一方で、これから示すように次の命題が成り立つ:

Claim 1: 任意の \(v \in V\) に対して、次の不等式が成り立つ:

\[ \left(\text{\# } v \in J_{\sigma} \text{ を満たす } V \text{-列挙} \right) \geq \dfrac{\left(\text{\# } V \text{-列挙}\right) }{1+\deg v} \]

[Claim 1 の証明: \(v \in V\) を任意に取って固定する。\(\deg^{\prime}v\) を \(v\) の隣接頂点の個数と定義する。明らかに \(\deg^{\prime}v\leq\deg v\) が成り立つ。

\(V\)-列挙 \(\sigma\) において、頂点 \(v\) が自身の任意の隣接頂点より前にあるとき、\(\sigma\) を優秀 (good) と呼ぶことにする。\(J_{\sigma}\) の定義より、\(V\)-列挙 \(\sigma\) が優秀なのは \(v\in J_{\sigma}\) のとき、かつそのときに限る。よって次の等式を示せばよい:

\[ \left(\text{\# } \text{優秀な } V \text{-列挙}\right) \geq \dfrac{\left(\text{\# } V \text{-列挙} \right) }{1+\deg v} \]

写像 \(\Gamma\colon \left\{V\text{-列挙}\right\} \rightarrow\left\{\text{優秀な } V\text{-列挙}\right\}\) を次のように定義する: 任意の \(V\)-列挙 \(\tau\) に対して、\(\tau\) が優秀なら \(\Gamma(\tau) = \tau\) と定め、そうでないなら \(\tau\) で最初に現れる \(v\) の隣接頂点と \(v\) を交換して得られる \(v\) 列挙を \(\Gamma (\tau)\) と定める。この写像 \(\Gamma\) は \(\left( 1+\deg^{\prime}v\right) \) 対 \(1\) の対応である ── つまり、優秀な \(V\)-列挙 \(\sigma\) のそれぞれに対して、\(\Gamma\left( \tau\right) =\sigma\) を満たす \(V\)-列挙 \(\tau\) がちょうど \(1+\deg^{\prime}v\) 個だけ存在する (具体的に言えば、そういった \(\tau\) の一つは \(\sigma\) 自身であり、他の \(\deg^{\prime}v\) 個は \(\sigma\) で \(v\) の任意の隣接頂点と \(v\) を交換すると得られる)。よって multijection principle³ より、次の等式が分かる:

\[ \begin{aligned} \left\vert \left\{V \text{-列挙}\right\} \right\vert &= \left(1+\deg^{\prime}v\right) \cdot \left\vert \left\{ \text{優秀な }V\text{-列挙}\right\} \right\vert \\ \therefore \ \left(\text{\# } V \text{-列挙} \right) &= \left(1+\deg^{\prime}v\right) \cdot \left(\text{\# } \text{優秀な } V \text{-列挙}\right) \end{aligned} \]

これと \(\deg^{\prime}v\leq\deg v\) より、次の不等式を得る:

\[ \left(\text{\# } \text{優秀な } V \text{-列挙}\right) = \dfrac{\left(\text{\# } V \text{-列挙} \right) }{1+\deg^{\prime}v}\geq \dfrac{\left(\text{\# } V \text{-列挙} \right) }{1+\deg v} \]

「優秀な \(V\)-列挙」とは「\(v\in J_{\sigma}\) を満たす \(V\)-列挙 \(\sigma\)」のことだから、これで Claim 1 は証明された。]

次に、Iverson の括弧記法 (定義 5.14.2) の基礎的な性質を確認しておく。\(S\) を有限集合、\(T\) を \(S\) の部分集合とするとき、次の等式が成り立つ:

\[ \left\vert T\right\vert =\sum_{v\in S}\left[ v\in T\right] \qquad (3) \]

[実際、\(\left[ v\in T\right]\) は任意の \(v \in T\) に対して \(1\) となり、任意の \(v\in S\setminus T\) に対して \(0\) となる。よって右辺の和は \(\left\vert T\right\vert \cdot1+\left\vert S\setminus T\right\vert \cdot0=\left\vert T\right\vert \) に等しい。]

不等式 \((2)\) から次が分かる:

\[ \begin{aligned} \left(\text{\# } V \text{-列挙}\right) \cdot\sum_{v\in V}\dfrac{1}{1+\deg v} & > \sum_{\sigma:\, V \text{-列挙}} \left\vert J_{\sigma}\right\vert \\ & = \sum_{\sigma:\, V \text{-列挙}}\ \ \sum\limits_{v\in V} \left[ v\in J_{\sigma}\right] \qquad (\because\ \text{式 } (3)) \\ & =\sum\limits_{v\in V}\ \ \sum_{\sigma:\, V \text{-列挙}}\left[ v\in J_{\sigma}\right] \\ & =\sum\limits_{v\in V} \left(\text{\# } v\in J_{\sigma} \text{ を満たす } V \text{-列挙 } \sigma \right) \\ & \geq \sum\limits_{v\in V}\dfrac{\left(\text{\# } V \text{-列挙} \right) }{1+\deg v} \qquad (\because\ \text{Claim 1}) \\ & = \left(\text{\# } V \text{-列挙}\right) \cdot\sum_{v\in V}\dfrac{1}{1+\deg v} \end{aligned} \]

これは矛盾である: 自分自身より小さい実数は存在しない。矛盾が得られたので、定理 7.1.3 は証明された。□

Remark 7.1.5

この証明は確率的証明 (probabilistic proof) の例である。なぜだろうか？この証明に含まれる「和」を使った議論は、「平均」を使った議論へと容易に書き換えられる。例えば Claim 1 は「任意の頂点 \(v\) に対して、(一様ランダムに取った) \(V\)-列挙 \(\sigma\) が \(v\in J_{\sigma}\) を満たす確率は \(\dfrac{1}{1+\deg v}\) 以上である」となる。ここから \(\left\vert J_{\sigma}\right\vert \) の期待値は (期待値の線形性より) \(\sum\limits_{v\in V}\dfrac{\vphantom{\Large 1} 1}{1+\deg v}\) 以上と分かり、少なくとも一つの \(V\)-列挙 \(\sigma\) は \(\left\vert J_{\sigma}\right\vert \geq\sum\limits_{v\in V}\dfrac{1}{1+\deg v}\) を満たすと結論できる。つまり一つ目の証明は確率と期待値の言葉を使って書き換えることができる。

なお、要素数が \(\sum\limits_{v\in V}\dfrac {1}{1+\deg v}\) 以上の独立集合を実際に構築することを考えるとき、この証明は (そのままでは) 役に立たない。この証明からは「考えられる \(V\)-列挙 \(\sigma\) のそれぞれに対して部分集合 \(J_{\sigma}\) を計算していけば、いずれ条件を満たす独立集合が見つかる」ことが分かるに過ぎない。この構築が必要とするステップ数は \(V\) の部分集合の個数よりさらに多い。

また、「任意の \(V\)-列挙 \(\sigma\) の少なくとも半分が \(\left\vert J_{\sigma}\right\vert \geq \sum\limits_{v\in V}\dfrac{1}{1+\deg v}\) を満たす」は成り立たない点に注意してほしい。平均値と中央値は異なる！

二つ目の証明を次に示す。この証明からは良いアルゴリズムが得られる:

[定理 7.1.3 の二つ目の証明] \(\left\vert V\right\vert \) に関する強い数学的帰納法で示す。\(p \in \mathbb{N}\) を任意に取って固定し、頂点の個数が \(p\) より小さい任意のループレスな多重グラフ \(G\) に対して定理 7.1.3 が証明されていると (帰納法の仮定として) 仮定する。この上で、\(p\) 個の頂点を持つループレスな多重グラフ \(G=\left( V,E,\varphi\right) \) に対しても同じ命題が成り立つと示せばよい。

\(\left\vert V\right\vert =0\) なら示すべき命題は明らかである (\(\varnothing\) が条件を満たす独立集合であるため)。よって一般性を失うことなく \(\left\vert V\right\vert \neq0\) と仮定する。さらに、\(G\) が単純グラフと仮定しても一般性は失われない (そうでなければ \(G\) を \(G^{\operatorname*{simp}}\) で置き換える。こうしたとき任意の頂点 \(v \in V\) の次数 \(\deg v\) は大きくならないので、\(G^{\operatorname*{simp}}\) に対する定理 7.1.3 は \(G\) に対する定理 7.1.3 を含む)。

\(\left\vert V\right\vert \neq0\) より、\(\deg_{G}u\) が最小となる頂点 \(u \in V\) が存在する⁴。この \(u\) に関して次の等式が成り立つ:

\[ \deg_{G}v\geq\deg_{G}u \quad (\forall v\in V) \qquad (4) \]

\(U\colonequals \left\{ u\right\} \cup\left\{ u \text{ の隣接頂点} \right\} \) と定める。明らかに \(U\subseteq V\) であり、\(G\) が単純グラフであることから \(\left\vert U\right\vert =1+\deg_{G}u\) も分かる。

\(V \setminus U\) に関する \(G\) の誘導部分グラフを \(G^{\prime}\) とする。これは \(U\) に属する頂点 (およびそれらを含む辺) を \(G\) から除去して得られるグラフである。このとき \(G^{\prime}\) の頂点は \(G\) の頂点より少ないので、\(G^{\prime}\) の頂点の個数は \(p\) より小さい。よって帰納法の仮定より、\(G^{\prime}\) に対する定理 7.1.3 は成立する。言い換えれば、\(G^{\prime}\) は要素数が

\[ \sum_{v\in V\setminus U}\dfrac{1}{1+\deg_{G^{\prime}}v} \]

以上の独立集合を持つ。そのような独立集合を一つ取って \(T\) として、\(S\colonequals \left\{ u\right\} \cup T\) と定める。すると \(T\subseteq V\setminus U\) より \(u\) の隣接頂点は \(T\) に含まれないので、\(S\) は \(G\) の独立集合である。加えて、次に示すように \(\left\vert S\right\vert \geq\sum\limits_{v\in V}\dfrac{1}{1+\deg_{G}v}\) も成り立つ:

\[ \begin{aligned} \sum\limits_{v\in V}\dfrac{1}{1+\deg_{G}v} & = \sum\limits_{v\in U}\underbrace{\dfrac{1}{1+\deg_{G}v}} _{\substack{\displaystyle \small \leq\dfrac{1}{1+\deg_{G}u}\\[12pt] (\because\ \text{式 } (4) \text{ より})}} + \sum\limits_{v\in V\setminus U} \hspace{-17.5pt}\underbrace{\dfrac{1}{1+\deg_{G}v}} _{\substack{\displaystyle \small \leq\dfrac{1}{1+\deg _{G^{\prime}}v}\\[12pt] \left(\substack{\because\ G^{\prime} \text{ は } G \text{ の部分グラフより}\\[3pt] \deg_{G}v\geq\deg_{G^{\prime}}v} \right)}}\\[70pt] & \leq\underbrace{\sum\limits_{v\in U}\dfrac{1}{1+\deg_{G}u}} _{\substack{=\displaystyle \small \left \vert U\right\vert \cdot\dfrac{1}{1+\deg_{G}u} = 1\\[12pt] (\because\ \left\vert U\right\vert =1+\deg_{G}u)}} \hspace{15pt}+ \hspace{-15pt} \underbrace{\sum\limits_{v\in V\setminus U}\dfrac{1}{1+\deg_{G^{\prime}}v}} _{\substack{\displaystyle \small \leq\left\vert T\right\vert \\[8pt] \left(\because\ T \text{ の要素数は } {\displaystyle \small \sum_{v\in V\setminus U}\dfrac{1}{1+\deg_{G^{\prime}}v}} \text{ 以上}\right)}}\\[55pt] & \leq1+\left\vert T\right\vert \\[5pt] & = \left\vert S\right\vert \quad \left(\because\ S=\left\{ u\right\} \cup T\right) \end{aligned} \]

これで要素数が \(\sum\limits_{v\in V}\dfrac{1}{1+\deg_{G}v}\) 以上の \(G\) の独立集合 \(S\) が見つかった。つまり \(G\) に対しても定理 7.1.3 は成り立つ。以上で帰納ステップが完了したから、定理 7.1.3 は証明された。□

Remark 7.1.6

定理 7.1.3 の二つ目の証明は (一つ目の証明と異なり) 条件を満たす独立集合を見つけるまずまず効率的なアルゴリズムを与える。しかし、二つの証明が根本的に異なるわけではない: 条件付確率の手法 (method of conditional probabilities)による脱乱択化 (derandomization)を行うと、一つ目の証明から二つ目の証明を導ける。条件付確率の手法は脱乱択化の一般的なテクニックである。条件付確率の手法を適用するには創意工夫が必要な場合も多く、常に適用できるとも限らない。ただ、今考えている証明は適用できる例である。脱乱択化について詳しくは [Aspnes23, Chapter 13] を見てほしい。

組合せ論における確率的証明に関しては [Chen14] と [AloSpe16] が詳しい。確率的証明を利用できる問題を二つ示す:

練習問題 7.1

\(G=\left( V,E\right) \) を単純グラフとする。\(G\) の各頂点が \(1\) 以上の次数を持つと仮定する。次の条件を満たす \(V\) の部分集合 \(S\) が存在することを示せ:

\(S\) の要素数は \(\displaystyle \sum_{v\in V}\dfrac{2}{1+\deg v}\) 以上である。
誘導部分グラフ \(G\left[ S\right] \) は森である。

[ヒント: グラフを考えれば分かるように、この命題は (定理 7.1.3 と異なり) ループレスな多重グラフに対しては成立しない。]

練習問題 7.2

\(n\) を正整数とする。\(\dfrac{n!}{2^{n-1}}\) 個以上のハミルトン路を持つ \(n\) 頂点のトーナメントが存在することを示せ。

もちろん厳密に言えば等しくない: 独立集合は単なる頂点の集合であるのに対して、誘導部分グラフはグラフである。正確に言えば、\(\operatorname*{V}\left( G\right) \) の部分集合 \(S\) が独立集合となるのは、誘導部分グラフ \(G\left[ S\right] \) が辺を持たないとき、かつそのときに限る。 ↩︎
定理 7.1.3 で「\(G\) がループレスである」という仮定は欠かせないことに注意してほしい。もし \(G\) が各頂点にループを持っていたら、\(\varnothing\) だけが \(G\) の独立集合となる。 ↩︎
multijection principle については定理 5.10.4 の証明 (第 5.11 節) にある脚注で説明した。 ↩︎
ここで \(\deg_{H}u\) はグラフ \(H\) における頂点 \(u\) の次数を意味する。 ↩︎