7.3. Turán の定理の証明
Turán の定理 (定理 2.4.8) には証明を与えていなかった。この定理は前節で示した系 7.2.1 を使うと容易に証明できる。読みやすいように、Turán の定理をここに繰り返しておく:
\(r\) を正整数、\(G\) を \(n\) 個の頂点と \(e\) 個の辺を持つ単純グラフとする。このとき
が成り立つなら、相互に隣接する \(r+1\) 個の相異なる頂点が \(G\) に存在する。
単純グラフ \(G\) を \(G=\left( V,E\right) \) と書く。このとき \(\left\vert V\right\vert =n\) と \(\left\vert E\right\vert =e\) と \(E\subseteq\mathcal{P}_{2}\left( V\right) \) が成り立つ。
\(\overline{E}\colonequals \mathcal{P}_{2}\left( V\right) \setminus E\) と定める。つまり、\(G\) の非辺 (non-edge) の集合を \(\overline{E}\) とする ── \(V\) の要素の組であって \(G\) の辺でないものが \(\overline{E}\) の要素となる。次の等式は明らかに分かる:
\(\overline{G}\) を単純グラフ \(\left( V,\overline{E}\right) \) とする。\(\overline{G}\) は \(G\) の補グラフ (complementary graph) と呼ばれる。\(G\) の補グラフ \(\overline{G}\) は \(n\) 個の頂点を持ち、\(\left\vert \overline{E}\right\vert =\dbinom {n}{2}-e\) の辺を持つ1。系 7.2.1 で \(G = \overline{G}\) および \(m = \dbinom{n}{2}-e\) とすれば、要素数が
以上の独立集合が \(\overline{G}\) に存在すると分かる。この独立集合を \(S\) とすれば、\(\left\vert S\right\vert\) は次の不等式を満たす:
\(\left\vert S\right\vert \) と \(r\) は整数だから、この不等式から \(\left\vert S\right\vert \geq r+1\) が分かる。一方、\(S\) は \(\overline{G}\) の独立集合なので、\(S\) の任意の二頂点は \(\overline{G}\) で隣接しない。よって \(\overline{G}\) の定義より、\(S\) の任意の二頂点は \(G\) で隣接する。\(\left\vert S\right\vert \geq r+1\) だから、\(S\) の要素は相互に隣接する \(r + 1\) 個 (以上) の相異なる \(G\) の頂点である。以上で定理 7.3.1 は証明された。□
[AigZie18, Chapter 41] と [Zhao23, § 1.2] には、ここに示したものとは異なる定理 7.3.1 の美しい証明が載っている。
-
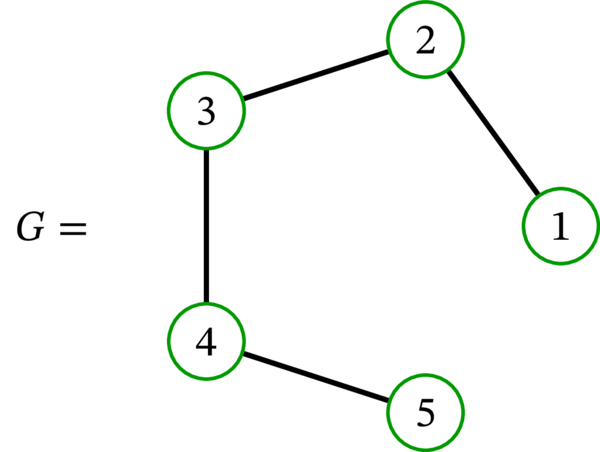
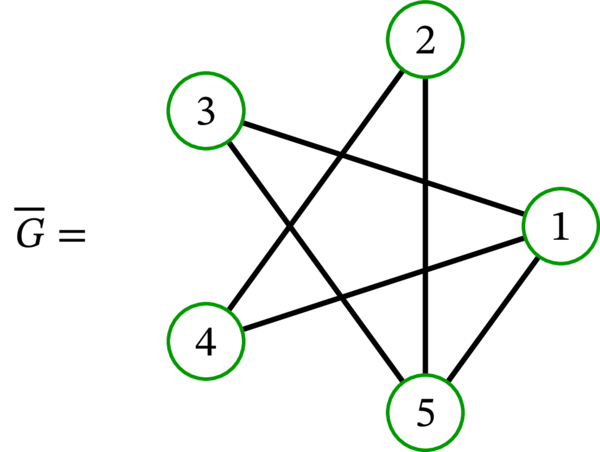
\(G\) と \(\overline{G}\) の例を示す:
\(\overline{G}\) で任意の二頂点間に辺が存在するのは、同じ二頂点間に \(G\) で辺が存在しないとき、かつそのときに限る。 ↩︎