8.1. マッチングの定義

\(G\) を次の単純グラフとする:

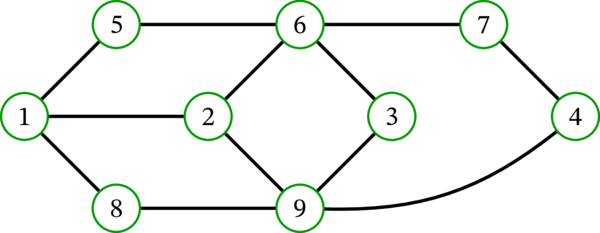
• 集合 \(\left\{ 12,\ 36,\ 47\right\} \) は \(G\) のマッチングである。このマッチングを \(M\) とすれば、\(M\) でマッチ済みの頂点は \(1\), \(2\), \(3\), \(4\), \(6\), \(7\) であり、これらの頂点の \(M\)-パートナーはそれぞれ \(2\), \(1\), \(6\), \(7\), \(3\), \(4\) である。\(M\) は完全でないものの、例えば \(\left\{ 1,3,4\right\} \)-完全あるいは \(\left\{ 1,2,3,4,6,7\right\} \)-完全ではある。

• 集合 \(\left\{ 12,\ 36,\ 67\right\} \) は \(G\) のマッチングでない。二つの異なる要素 \(36\) と \(67\) が共通の端点 \(6\) を持つためである。

• 集合 \(\varnothing\), \(\left\{ 36\right\} \), \(\left\{ 15,\ 29,\ 36,\ 47\right\} \) はどれも \(G\) のマッチングである。

\(n\), \(m\) を正整数とする。\(n\) 次の路グラフ \(P_{n}\) と \(m\) 次の路グラフ \(P_{m}\) のデカルト積 \(P_{n}\times P_{m}\) は \( n \times m \) の格子グラフ (grid graph) と呼ばれ、次の形をしている:

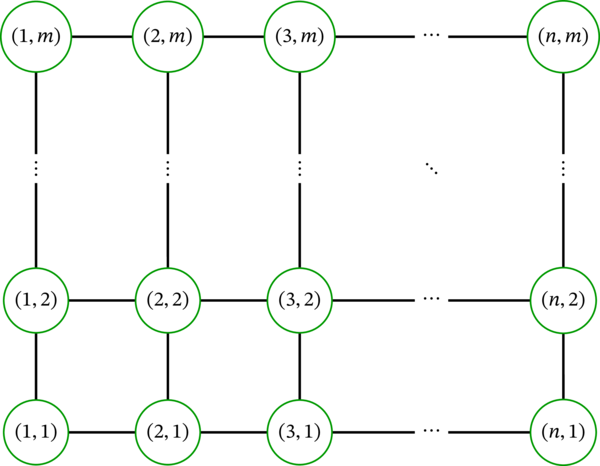
1. \(n\) が偶数なら、次の集合は \(P_{n}\times P_{m}\) の完全マッチングである:

   \[ \left\{ \left\{ \left( i,j\right) ,\ \left( i+1,j\right) \right\} \mid i \in \left\{1,3,\ldots,n-1\right\} \ \wedge \ j \in \left\{1,2,\ldots,m\right\} \right\} \]

   例えば \(n=4\), \(\ m=3\) のとき、この集合を次に示す:

   

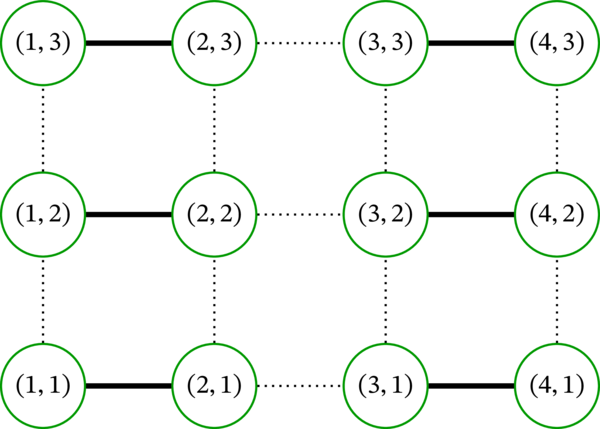
   実線がマッチングに属する辺を、破線がマッチングに属さない辺を表す。

2. 同様に、\(m\) が偶数のとき次の集合は \(P_{n}\times P_{m}\) の完全マッチングである:

   \[ \left\{ \left\{ \left( i,j\right) ,\ \left( i,j+1\right) \right\} \mid i \in \left\{1,2,\ldots,n\right\}, \ j \in \left\{1,3,\ldots,m-1 \right\}\right\} \]

3. \(n\) と \(m\) が両方とも奇数なら、\(P_{n}\times P_{m}\) は完全マッチングを持たない。一般に、奇数個の頂点を持つ任意のループレスな多重グラフ \(G\) は完全マッチングを持たない。そういったグラフのマッチングは必ず偶数個の頂点を被覆する¹ためである。

「二本の角を持った五角形グラフ」 \(C_{5}^{\prime\prime}\) (この用語は標準的ではない。読者が理解できることを願う) は次のグラフである:

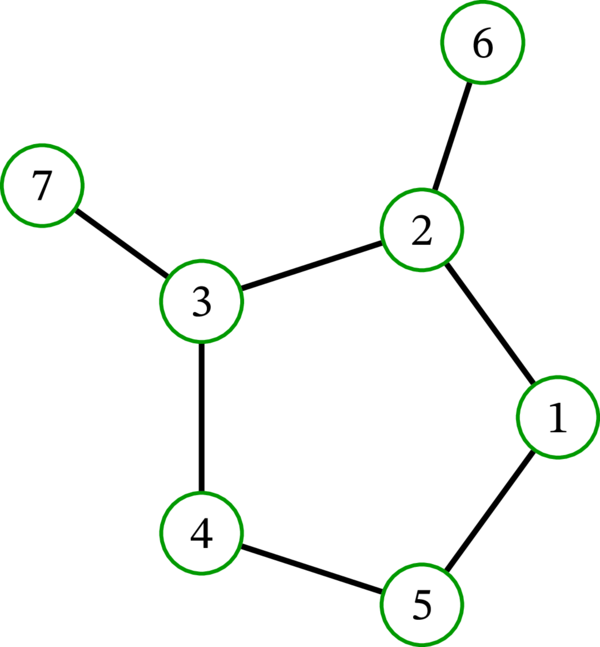
\(C_{5}^{\prime\prime}\) は完全マッチングを持たない。これは容易に分かる: \(C_{5}^{\prime\prime}\) はループレスなので、任意の辺は二つの頂点を含む。よって \(C_{5}^{\prime\prime}\) の任意のマッチング \(M\) では \(2\cdot\left\vert M\right\vert \) 個の頂点がマッチ済みとなる。特に、\(C_{5}^{\prime\prime}\) の任意のマッチングでは偶数個の頂点がマッチ済みとなる。\(C_{5}^{\prime\prime}\) は奇数個の頂点を持つから、完全マッチングを持たない。

\(C_{5}^{\prime\prime}\) のマッチングの最大要素数はいくつだろうか？ 二要素集合 \(\left\{ 12,\ 34\right\} \) は \(C_{5}^{\prime\prime}\) のマッチングであり、この集合に他の任意の辺を加えるとマッチングでなくなる。ここからマッチングの最大要素数が \(2\) だと考えたくなるかもしれないが、これは正しくない。実際、\(3\) 要素のマッチング \(\left\{ 12,\ 37,\ 45\right\} \) が存在する。このマッチングは本当に要素数最大である。