8.2. 二部グラフ
二部グラフ (bipartite graph) とは、次の条件を満たす三つ組 \(\left( G,X,Y\right) \) を意味する:
-
\(G=\left( V,E,\varphi\right) \) は多重グラフである。
-
\(X\) と \(Y\) は共通要素を持たない \(V\) の部分集合であり、\(X\cup Y=V\) を満たす。
-
\(G\) の任意の辺は \(X\) に属する端点と \(Y\) に属する端点を持つ。
\(6\) 次の閉路グラフ \(C_{6}\) を考える:
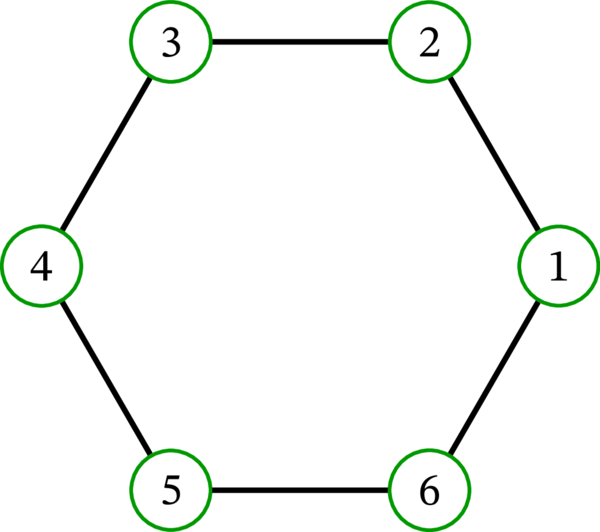
\(\left( C_{6},\ \left\{ 1,3,5\right\} ,\ \left\{ 2,4,6\right\} \right) \) は二部グラフである。なぜなら、\(G\) の各辺は \(\left\{ 1,3,5\right\} \) に属する端点と \(\left\{ 2,4,6\right\} \) に属する端点を持つからである。また、\(\left( C_{6},\ \left\{ 2,4,6\right\} ,\ \left\{ 1,3,5\right\} \right) \) も二部グラフである。
二部グラフ \(\left( G,X,Y\right) \) は単なるグラフ \(G\) ではなく頂点集合の部分集合 \(X\), \(Y\) と \(G\) を合わせたものである点に注意してほしい。そのため \(X\) と \(Y\) が異なれば、グラフ \(G\) が同じでも二部グラフとしては異なることがあり得る。例えば、二つの二部グラフ \(\left( C_{6},\ \left\{ 1,3,5\right\} ,\ \left\{ 2,4,6\right\} \right) \) と \(\left( C_{6},\ \left\{ 2,4,6\right\} ,\ \left\{ 1,3,5\right\} \right) \) は等しくない。
二部グラフ \(\left( G,X,Y\right) \) の描画では、\(X\) に属する頂点と \(Y\) に属する頂点をそれぞれ左右に配置した垂直な直線上に位置を揃えて書く場合が多い。例えば二部グラフ \(\left( C_{6},\ \left\{ 1,3,5\right\} ,\ \left\{ 2,4,6\right\} \right) \) は次のように描画できる:
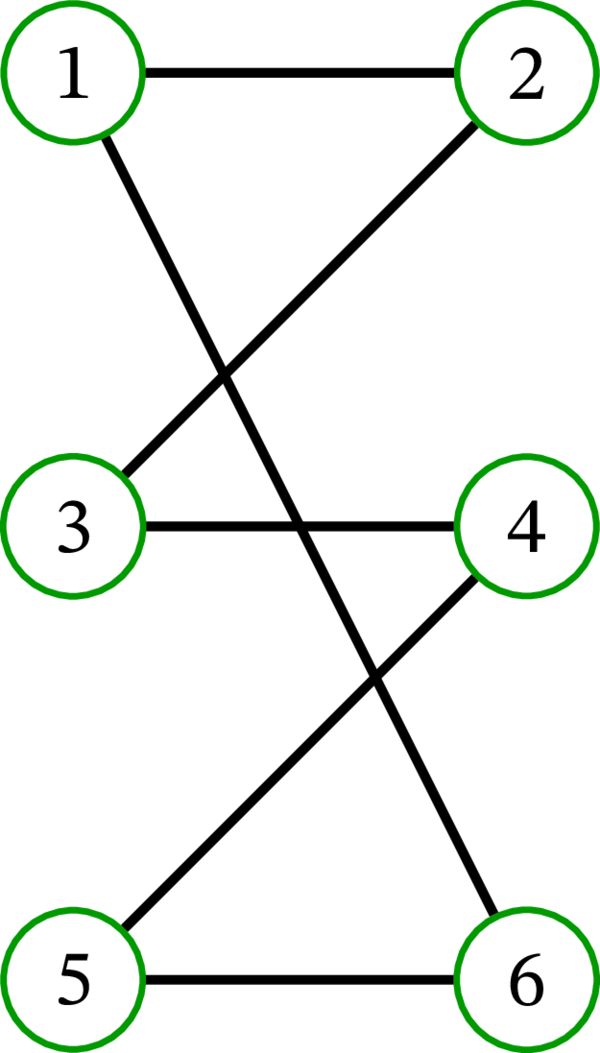
同様に、二部グラフ \(\left( C_{6},\ \left\{ 2,4,6\right\} ,\ \left\{ 1,3,5\right\} \right) \) は次のように描画できる:
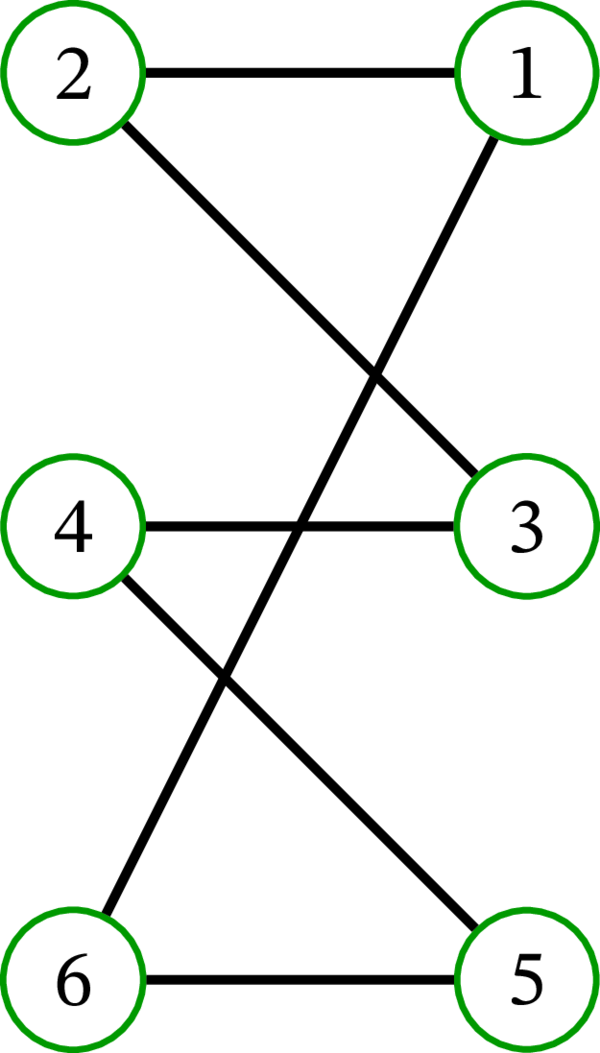
この例から、次の用語が示唆される:
\(\left( G,X,Y\right) \) を二部グラフとする。\(X\) に属する頂点を左頂点 (left vertex) と呼び、\(Y\) に属する頂点を右頂点 (right vertex) と呼ぶ。さらに、\(G\) の辺を二部グラフ \(\left( G,X,Y\right) \) の辺 (edge) と呼ぶ。
つまり、二部グラフの任意の辺は左頂点と右頂点を接続する。
二部グラフは適切な \(2\)-彩色を持った多重グラフと「同一」である。つまり次の命題が成り立つ:
\(G=\left( V,E,\varphi\right) \) を多重グラフとする。
-
\(\left( G,X,Y\right) \) が二部グラフなら、次の写像 \(f\) は \(G\) の適切な \(2\)-彩色である:
\[ \begin{aligned} f\colon V & \rightarrow\left\{ 1,2\right\} \\ v & \mapsto \begin{cases} 1 & (v \in X \text{ のとき}) \\ 2 & (v \in Y \text{ のとき}) \end{cases} \end{aligned} \] -
逆に、\(f\colon V\rightarrow\left\{ 1,2\right\} \) が \(G\) の適切な \(2\)-彩色なら、次のように定めた \(V_{1}\) と \(V_{2}\) に対する \(\left( G,V_{1},V_{2}\right) \) は二部グラフである:
\[ V_{i}\colonequals \left\{ f \text{ で色が } i \text{ の頂点}\right\} = \left\{ v \mid f (v) = i \right\} \quad (\forall i \in\left\{ 1,2\right\}) \] -
(a) と (b) の構築はそれぞれがもう一方の逆である。つまり、二部グラフから構築した適切な \(2\)-彩色を使って二部グラフを構築すると、元の二部グラフが得られる。また、適切な \(2\)-彩色から構築した二部グラフを使って適切な \(2\)-彩色を構築すると、元の適切な \(2\)-彩色が得られる。
定義を理解したかどうかの問題である。□
\(\left( G,X,Y\right) \) を二部グラフとする。このとき \(G\) は長さが奇数の回路を持たない。特に、\(G\) はループと三角形を持たない。
命題 8.2.4 (a) より \(G\) は適切な \(2\)-彩色を持つ。よって \(2\)-彩色の同値性定理 (定理 6.2.1) から、\(G\) は長さが奇数の回路を持たないと分かる。特に、\(G\) はループ (長さが \(1\) の回路) と三角形 (長さが \(3\) の回路) を持たない。□
以降で必要になる記法をさらに定義する:
\(G=\left( V,E,\varphi\right) \) を多重グラフ、\(U\) を \(V\) の部分集合とする。\(N \left(U\right)\) を次のように定める:
\(N \left(U\right)\) を \(U\) の隣接頂点集合 (neighbor set) と呼ぶ。
例 8.1.5 で示した「二本の角を持った五角形」を \(G\) とする。このとき次の等式が成り立つ:
二部グラフでは、隣接頂点集合が優れた性質を持つ:
\(\left( G,X,Y\right) \) を二部グラフとする。任意の \(A \subseteq X\) に対して次の包含関係が成り立つ:
頂点 \(v\in N\left( A\right) \) を任意に取る。このとき \(N\left( A\right) \) の定義より、\(v\) は \(A\) に属する隣接頂点を持つ。その隣接頂点を \(w\) とすれば \(w\in A\subseteq X\) が成り立つ。\(\left( G,X,Y\right) \) は二部グラフより \(X\) と \(Y\) は共通要素を持たないので、\(w \in X\) から \(w \notin Y\) が分かる。
\(w\) は \(v\) の隣接頂点なので、\(v\) と \(w\) を端点に持つ辺が存在する。\(\left( G,X,Y\right) \) は二部グラフなので、この辺は \(Y\) に属する頂点を含む。つまり \(v\) と \(w\) のいずれかは \(Y\) に属する。\(w \notin Y\) だったから、\(v \in Y\) が分かる。
任意の \(v\in N\left( A\right) \) が \(v\in Y\) を満たすと示せたので、\(N\left( A\right) \subseteq Y\) が証明された。□
\(\left( G,X,Y\right) \) を二部グラフとする。次の等式を示せ: