8.3. Hall の結婚定理

目次

どうすれば二部グラフが完全マッチング (あるいは \(X\)-完全マッチング) を持つかどうかを判定できるだろうか？ この質問に答える前に、まずは非常に簡単な命題をいくつか証明しておく:

命題 8.3.1

\(\left( G,X,Y\right) \) を二部グラフ、\(M\) を \(G\) のマッチングとする。このとき:

  1. 任意の \(x \in X\) の \(M\)-パートナーは (存在するなら) \(Y\) に属する。任意の \(x \in Y\) の \(M\)-パートナーは (存在するなら) \(X\) に属する。

  2. \(\left\vert M\right\vert \leq\left\vert X\right\vert \) と \(\left\vert M\right\vert \leq\left\vert Y\right\vert \) が成り立つ。

  3. \(M\) が \(X\)-完全なら \(\left\vert X\right\vert \leq\left\vert Y\right\vert \) が成り立つ。

  4. \(M\) が完全なら \(\left\vert X\right\vert =\left\vert Y\right\vert \) が成り立つ。

  5. \(\left\vert M\right\vert \geq\left\vert X\right\vert \) なら \(M\) は \(X\)-完全である。

  6. \(M\) が \(X\)-完全で \(\left\vert X\right\vert =\left\vert Y\right\vert \) なら、\(M\) は完全である。

[証明] \(\left( G,X,Y\right) \) が二部グラフなので、\(G\) の任意の辺は \(X\) に属する端点と \(Y\) に属する端点を持つ。よって特に、任意の \(M\)-辺は \(X\) に属する端点と \(Y\) に属する端点を持つ。また、\(M\) はマッチングより任意の二つの \(M\)-辺は共通する端点を持たない。

(a): \(M\)-辺が \(X\) に属する端点と \(Y\) に属する端点を持つ事実から従う。

(b): \(M\)-辺は \(X\) に属する端点を持つ。さらに、任意の二つの \(M\)-辺は端点を共有しないから、\(X\) は少なくとも \(\left\vert M\right\vert \) 個の異なる要素を持つ。\(\left\vert M\right\vert \leq\left\vert Y\right\vert \) も同様に示せる。

(c): \(M\) が \(X\)-完全だと仮定する。このとき \(X\) に属する任意の頂点は \(M\) でマッチ済みなので、それを含む \(M\)-辺が存在する。言い換えれば、任意の頂点 \(x \in X\) に対して、ある \(M\)-辺 \(m\) が存在して、\(x\) が \(m\) の端点となる。任意の二つの \(M\)-辺は共通の端点を持たないので、前文の事実から \(M\)-辺が少なくとも \(\left\vert X\right\vert \) 個あると分かる。つまり \(\left\vert X\right\vert \leq \left\vert M\right\vert\) が成り立つ。これと (b) より \(\left\vert X\right\vert \leq\left\vert M\right\vert \leq\left\vert Y\right\vert \) を得る。

(d): \(M\) が完全だと仮定する。このとき \(M\) は \(X\)-完全かつ \(Y\)-完全だから、(c) より \(\left\vert X\right\vert \leq\left\vert Y\right\vert \) が分かる。同様の議論で \(\left\vert Y\right\vert \leq\left\vert X\right\vert \) も分かるので、この二つの事実から \(\left\vert X\right\vert =\left\vert Y\right\vert \) を得る。

(e): \(\left\vert M\right\vert \geq\left\vert X\right\vert \) と仮定する。

任意の \(M\)-辺は \(X\) に属する端点を持つ。\(X\) に属する \(M\)-辺の端点は (任意の二つの \(M\)-辺は端点を共有しないので) 相異なるため、その個数は \(\left\vert M\right\vert \) 以上である。仮定より \(\left\vert M\right\vert \geq\left\vert X\right\vert \) だから、\(X\) に属する \(M\)-辺の端点の個数は \(\left\vert X\right\vert \) 以上と分かる。よって、\(X\) に属する任意の頂点は何らかの \(M\)-辺の端点である。つまり \(X\) の全ての頂点は \(M\) でマッチ済みであり、\(M\) は \(X\)-完全だと結論できる。

(f): \(M\) が \(X\)-完全で \(\left\vert X\right\vert =\left\vert Y\right\vert \) だと仮定する。

マッチング \(M\) が \(X\)-完全なので、全ての頂点 \(x \in X\) は \(M\) でマッチ済みである。(a) より、任意の頂点 \(x \in X\) の \(M\)-パートナーは \(Y\) に属する。つまり、任意の頂点 \(x \in X\) の \(M\)-パートナーは \(M\) でマッチ済みである。異なる頂点の \(M\)-パートナーは異なるので、\(Y\) に属する頂点の少なくとも \(\left\vert X\right\vert \) 個は \(M\) でマッチ済みと分かる。\(\left\vert X\right\vert =\left\vert Y\right\vert \) だから、\(Y\) に属する頂点の少なくとも \(\left\vert Y\right\vert \) 個はマッチ済みである。ここから \(Y\) に属する全ての頂点がマッチ済みだと結論できる (「\(Y\) に属する頂点の \(\left\vert Y\right\vert \) 個」は「\(Y\) に属する全ての頂点」に等しい)。\(X\) に属する全ての頂点もマッチ済みだったから、\(G\) の全ての頂点はマッチ済みだと分かる。言い換えれば \(M\) は完全である。□

例 8.3.2

次の二部グラフを考える:

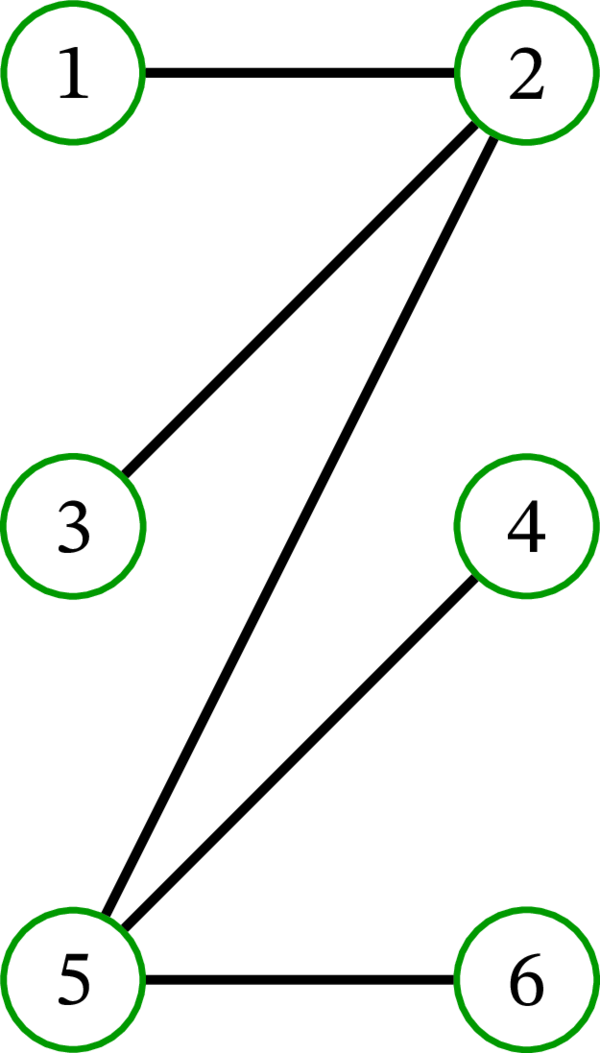
(例 8.2.2 で説明した方法で描画されている。) このグラフは完全マッチングを持つだろうか？ 正解は「持たない」である: 左頂点 \(1\), \(3\) のパートナーとなれる右頂点が \(2\) しか存在しない。

同様に、次の二部グラフも完全マッチングを持たない:

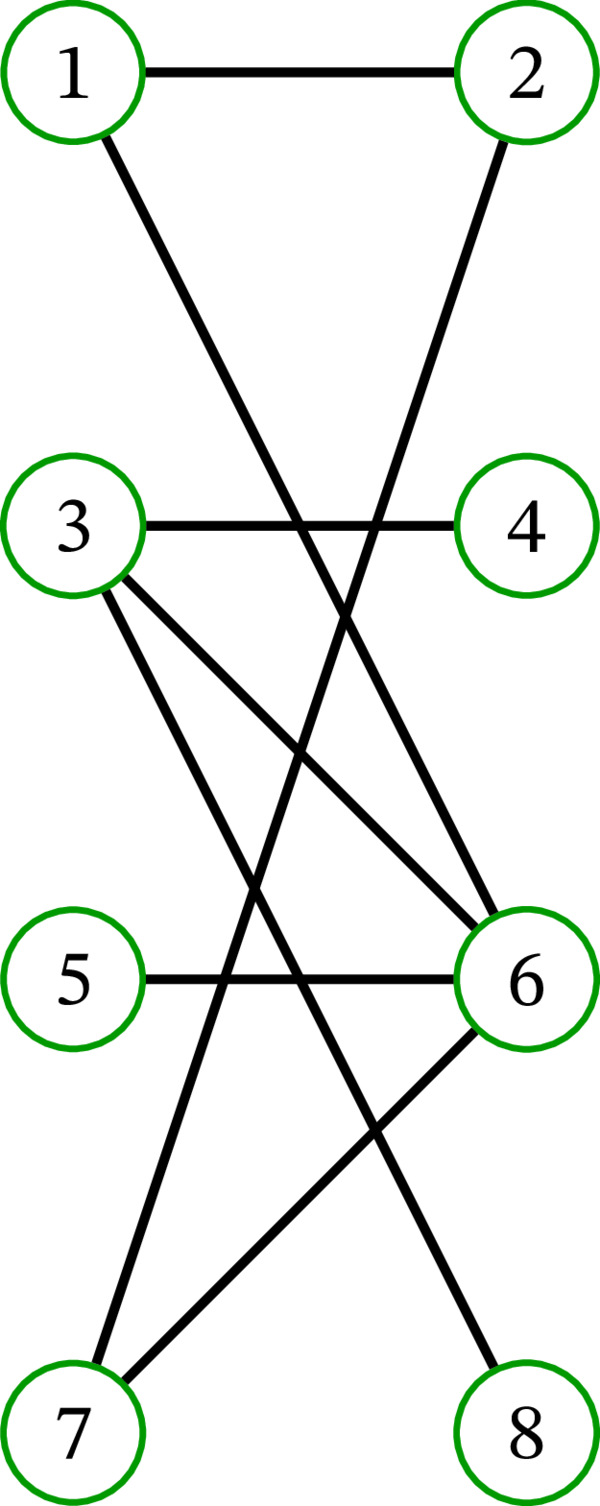
なぜなら、三つの左頂点 \(1\), \(5\), \(7\) のパートナーとなれる右頂点が \(2\) と \(6\) の二つしかないためである。

この例から分かるように、\(\left\vert N\left( A\right) \right\vert < \left\vert A\right\vert \) を満たす \(A \subseteq X\) があると、\(X\)-完全マッチングは作れない。この事実を肯定的な命題として示しておく:

命題 8.3.3

\(\left( G,X,Y\right) \) を二部グラフ、\(A\) を \(X\) の部分集合とする。\(G\) が \(X\)-完全マッチングを持つなら \(\left\vert N\left( A\right) \right\vert \geq\left\vert A\right\vert \) が成り立つ。

[証明] \(V\) を \(G\) の頂点集合とする。存在が仮定されている \(G\) の \(X\)-完全マッチングを \(M\) とする。このとき任意の \(x \in X\) は \(M\)-パートナーを持ち、次の写像 \(\mathbb{p}\) は単射である:

\[ \begin{aligned} \mathbf{p}\colon X & \rightarrow V\\ x & \mapsto\left( x \text{ の } M \text{-パートナー}\right) \end{aligned} \]

[二つの頂点が同じ \(M\)-パートナーを持つことはないため。] ここから \(\left\vert \mathbf{p}\left( A\right) \right\vert =\left\vert A\right\vert \) が分かる。一方、\(A\) に属する頂点の \(M\)-パートナーは \(N\left( A\right) \) に属するから、\(\left\vert \mathbf{p}\left( A\right) \right\vert \leq\left\vert N\left( A\right) \right\vert \) が成り立つ。よって \(\left\vert N\left( A\right) \right\vert \geq\left\vert \mathbf{p}\left( A\right) \right\vert =\left\vert A\right\vert \) が分かる。□

これで \(X\)-完全マッチングが存在するための必要条件が分かった。興味深いことに、これは十分条件でもある:

定理 8.3.4

[Hall の結婚定理 (Hall's marriage theorem)] \(\left( G,X,Y\right) \) を二部グラフとする。\(X\) の任意の部分集合 \(A\) が \(\left\vert N\left( A\right) \right\vert \geq\left\vert A\right\vert \) を満たすと仮定する。 [この仮定を Hall 条件 (Hall condition) と呼ぶ。]

このとき \(G\) は \(X\)-完全なマッチングを持つ。

この定理が「結婚定理」と呼ばれるのは、結婚相手を見つけようとしている男女のグループの関係が二部グラフとして解釈できるためである: \(X\) が男性全体の集合、\(Y\) が女性全体の集合を表し、男性 \(x \in X\) と女性 \(y \in Y\) は両想いのとき、かつそのときに限って隣接する。この設定では、\(X\)-完全なマッチングは男性全員をそれぞれ両想いの女性 (の一人) と結婚させる方法を表す。これは二部グラフの古典的なモデルであり、組合せ論の文献には必ず登場する。しかし、著者の知る限り現実世界で結婚相手を決めるために二部グラフが使われたことはない。しかしそうだとしても、これ以外の様々な状況で Hall の結婚定理は利用されている。例えばロジスティクスでは後述する一般化され有用性の大きく増した命題が利用される。Philip Hall は 1935 年に (私の理解が正しければ) 有限群に関する問題に取り組む中で結婚定理を (多少分かりにくい形で) 発見した。Wilhelm Maak も同年に解析学 (ほぼ周期的な関数に対する積分の概念の定義) で利用するために Hall の結婚定理を証明している。

Hall の結婚定理には様々な証明が知られている。非常に簡単な証明もある。自己充足的な短い証明は [LeLeMe18, § 12.5.2] と [Harju14, Theorem 3.9] から確認できる。本書では数十ページ後に証明を示すので楽しみにしておいてほしい。次節以降では Hall の結婚定理に関連する命題を説明し、その後二つの証明を示す:

広告
このページの文章はテキストゆれないくんを使って校正されました。