10.4. Elser 和

最後に (多重) 無向グラフの話題に戻る。次に示すのは Veit Elser が統計力学に関する研究の中で 1984 年に発見した補題である¹:

定理 10.4.1

[Elser の定理 (Elser's theorem, 大幅に書き換えたバージョン)] 少なくとも一つの辺を持つ多重グラフを \(G=\left( V,E,\varphi\right) \) とする。頂点 \(v\in V\) を一つ取って固定する。

\(F\subseteq E\) に対して、\(F\) に属する辺だけから構成される \(G\) の路を\(F\)-路 (\(F\)-path) と呼ぶ。言い換えれば、全域部分グラフ \(\left( V,F,\varphi|_{F}\right) \) の路が \(F\)-路である。

\(G\) の辺 \(e\in E\) と辺集合の部分集合 \(F\subseteq E\) に対して、\(v\) から \(e\) のいずれかの端点への \(F\)-路が存在するとき、\(F\) は \(e\) を汚染する (infect) と言う。 [この用語は、\(v\) で発生した病気が \(F\) に属する辺を通じて広がっていくイメージから命名されている。]

[辺 \(e\) が頂点 \(v\) を端点に持つとき、\(E\) の任意の (空集合を含む) 部分集合 \(F\) は \(e\) を汚染する。このとき自明な路 \(\left( v\right) \) が \(v\) から \(v\) への \(F\)-路となる。]

このとき次の等式が成り立つ:

\[ \sum_{\substack{\text{全ての辺 } e\in E \text{ を} \\[2pt] \text{汚染する } F\subseteq E}}\left(-1\right) ^{\left\vert F\right\vert }=0 \]

例 10.4.2

\(G=\left( V,E,\varphi\right) \) を次のグラフとする:

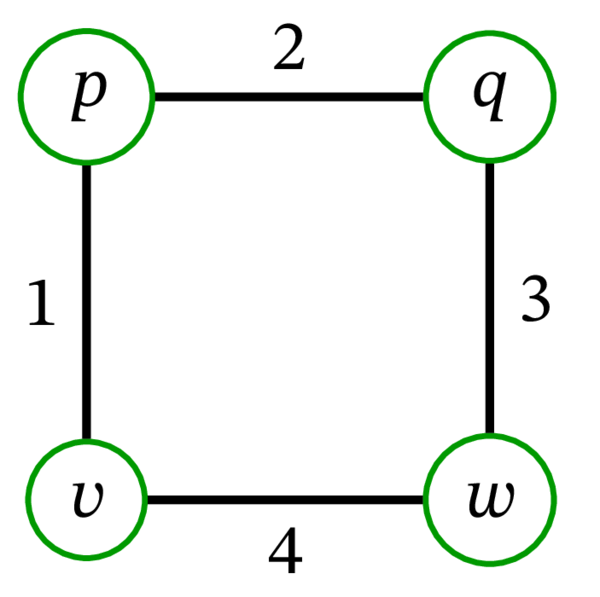
\(v\) のラベルが付いた頂点を \(v\) とするとき、\(G\) の全ての辺を汚染する \(E\) の部分集合は次の通りである:

\[ \begin{aligned} & \left\{ 1,2\right\} ,\ \ \left\{ 1,4\right\} ,\ \ \left\{ 3,4\right\},\ \ \left\{ 1,2,3\right\} ,\\ & \left\{ 1,3,4\right\},\ \ \left\{1,2,4\right\} ,\ \ \left\{ 2,3,4\right\} ,\ \ \left\{ 1,2,3,4\right\} \end{aligned} \]

よって次の等式が成り立つ:

\[ \begin{aligned} \sum_{\substack{\text{全ての辺 } e\in E \text{ を} \\[2pt] \text{汚染する } F\subseteq E}}\left(-1\right) ^{\left\vert F\right\vert } & =\left( -1\right) ^{2}+\left( -1\right) ^{2}+\left( -1\right) ^{2}+\left( -1\right) ^{3} \\[-17.5pt] & \qquad + \left( -1\right) ^{3}+\left( -1\right) ^{3}+\left( -1\right) ^{3}+\left( -1\right) ^{4}\\ & =0 \end{aligned} \]

これは定理 10.4.1 の主張と一致する。

Remark 10.4.3

辺ではなく頂点を汚染する \(F \subseteq E\) を考える方が自然に思えたかもしれない。しかし、定理 10.4.1 の「全ての辺 \(e \in E\)」を「全ての頂点 \(v \in V\)」に置き換えた命題は成り立たない。例 10.4.2 のグラフ \(G\) が反例となる。

なお、加えて \(F\subseteq E\) を \(W\subseteq V\) に置き換えた命題 (命題 10.4.4) は成り立つ。

[定理 10.4.1 の証明] Elser による証明は多少複雑である。別証明は [Grinbe21, Theorem 1.2] から確認できる。これは初等的で簡潔な証明だと (自分のことながら) 私は思っている。

次の事実に気が付けば、[Grinbe21, Theorem 1.2] に示した証明を思いつくのは難しくない: 定理 10.4.1 を証明するには次の等式を示せば十分である:

\[ \sum_{\substack{\text{全ての辺 } e\in E \text{ を} \\[2pt] \text{汚染\textbf{しない} } F\subseteq E}}\left(-1\right) ^{\left\vert F\right\vert }=0 \]

[全ての部分集合にわたる和 \(\displaystyle \sum_{F\subseteq E}\left( -1\right) ^{\left\vert F\right\vert }\) は \(0\) に等しいことが知られているため。] この等式を証明するために、集合 \(E\) 上に全順序を定義する (どんな順序でも構わないので、任意に辺を一列に並べる)。全ての辺 \(e \in E\) を汚染しない \(F\subseteq E\) に対して、\(F\) によって汚染されない辺の中で先述の全順序において最も小さい辺を \(\varepsilon\left( F\right) \) と定める。このとき、\(F\subseteq E\) が全ての辺 \(e \in E\) を汚染しないなら、集合² \(F^{\prime}\colonequals F\bigtriangleup\left\{ \varepsilon\left( F\right) \right\} \) (具体的に言えば、\(\varepsilon\left( F\right) \notin F\) なら \(F\) に \(\varepsilon\left( F\right) \) を加え、\(\varepsilon\left( F\right) \in F\) なら \(F\) から \(\varepsilon\left( F\right) \) を除去する操作によって得られる集合) も同じ性質を持ち、さらに \(\varepsilon\left( F^{\prime}\right) =\varepsilon\left( F\right) \) が成り立つことが示せる。よって、和 \(\displaystyle \sum_{\substack{\text{全ての辺 } e\in E \text{ を} \\[2pt] \text{汚染\textbf{しない} } F\subseteq E}}\left(-1\right) ^{\left\vert F\right\vert }\) で足されている項は組ごとに打ち消し合う (具体的に言えば、集合 \(F\) に対応する項は集合 \(F^{\prime}=F\bigtriangleup \left\{ \varepsilon\left( F\right) \right\} \) に対応する項と打ち消し合う)。つまり全体の和は \(0\) だと結論できる。□

Elser の定理も一般化を通じて改善できる。定理 10.3.1と同様に、全ての「パンデミックを起こさない部分集合」(全ての辺を汚染しない \(F \subseteq E\)) からなる集合を単体複体として扱い、この複体を位相空間として解析する。このとき、定理 10.4.1 の主張は対応する位相空間の被約 Euler 標数が \(0\) だと言っているのに等しい。また、この空間が可縮 (点とホモトピー同値) であることも示せる。さらに、パンデミックを起こさない部分集合から構成される単体複体は collapsible でもある (可縮性より強い組合せ論的な性質を持つ)。こういった用語の定義と命題の証明は [Grinbe21, § 5] から確認できる。

Elser の定理の設定を一般化することもできる。例えば、患者第一号 (patient zero) を一つの頂点 \(v\) ではなく頂点の集合とするアプローチが考えられる。Dorpalen-Barry, Hettle, Livingston, Martin, Nasr, Vega, Whitlatch による最近公開された論文 [DHLetc19] はこの設定の下での結果をいくつか示し、さらなる問題を提示している (その一部は 2022 年現在でも未解決である)。

Elser の定理の基礎的な部分に関する一般化も存在する: この定理はグラフと点に関する命題ではなく、私が「shade map」と呼ぶ一般的な構造に関する特定の和が \(0\) になると主張する命題だと解釈できる。この一般化の詳細は [Grinbe21, § 4] から確認できる。ここで shade map の説明はしないものの、[Grinbe21, Theorem 3.2] のもう一つの特殊ケースとして定理 10.4.1 の辺を頂点に置き換えた命題を次に示しておく:

定理 10.4.4

少なくとも二つの頂点を持つ多重グラフを \(G=\left( V,E,\varphi\right) \) とする。頂点 \(v \in V\) を任意に取って固定する。

\(W\subseteq V\) に対して、内部頂点が全て \(W\) に属する路を \(W\)-頂点路 (\(W\)-vertex-path) と呼ぶ。 [路 \(\mathbf{p}\) の内部頂点とは、始点でも終点でもない \(\mathbf{p}\) の頂点を言う。] [長さが \(1\) 以下の路は内部頂点を持たないので、任意の \(W \subseteq V\) に対して \(W\)-頂点路となる。]

\(G\) の頂点 \(w\in V\setminus\left\{ v\right\} \) と頂点集合の部分集合 \(W\subseteq V\setminus\left\{ v\right\} \) に対して、\(v\) から \(w\) への \(W\)-頂点路が存在するとき、\(W\) は \(w\) を頂点汚染する (\(W\) vertex-infects \(w\)) と言う。 [\(w\) が \(v\) の隣接頂点なら、任意の \(W \subseteq V\) は \(w\) を汚染する。]

このとき、次の等式が成り立つ:

\[ \sum_{\substack{\text{全ての頂点 } w\in V\setminus\left\{ v\right\} \text{ を}\\[3pt] \text{頂点汚染する} W\subseteq V\setminus\left\{ v\right\} }}\left( -1\right) ^{\left\vert W\right\vert }=0 \]

この補題は Elser による結果を大幅に言い換えたものであり、もはや原形をとどめていない。定理 10.4.1 が [Elser84, Lemma 1] を含むことの説明は [Grinbe21, Remark 1.4] にある。 ↩︎
記号 \(\bigtriangleup\) は二つの集合の対称差を表す。その定義は次の通りである: 二つの集合 \(X\), \(Y\) の対称差 (symmetric difference) \(X\bigtriangleup Y\) は次の集合として定義される:

\[ \begin{aligned} \left( X\cup Y\right) \setminus\left( X\cap Y\right) & =\left( X\setminus Y\right) \cup\left( Y\setminus X\right) \\ & =\left\{ X \text{ と }Y \text{ の\textbf{ちょうど一方だけ}に属する要素}\right\} \end{aligned} \]
↩︎