10.1. Menger の定理
本章では最初に Menger の定理 (Menger's theorems) と呼ばれる一連の結果を見ていく。この定理は Karl Menger にちなんで名付けられており、彼は 1927 年に曲線のトポロジーに関する研究の補助的な結果として Menger の定理の一つを発見した (この定理の歴史については [Schrij03, § 9.6e] を参照してほしい)。
フィラデルフィアからニューヨークに車で移動するルートが \(4\) つあるとしよう。それぞれのルートは異なる道路を使う (\(2\) つ以上のルートに利用される道路は存在しない) と仮定する。このとき、どんな \(3\) つの道路が封鎖されたとしても、フィラデルフィアからニューヨークに行くルートは少なくとも一つ必ず残る。
これは明らかである (実際、封鎖される道路はそれぞれが \(4\) つのルートの最大でも一つを利用不可能にするので、\(3\) つの道路が封鎖された場合でも少なくとも \(1\) つのルートは利用可能なままとなる)。この逆はより興味深い問題になる: フィラデルフィアとニューヨークの間にある道路が十分に複雑で、任意の \(3\) つの道路を封鎖してもフィラデルフィアからニューヨークまで移動できるとする。このとき、フィラデルフィアからニューヨークへの同じ道路を使わない \(4\) つのルートが必ず存在すると言えるだろうか?
Menger の定理を使うと、この問題 (および設定を少し変えた様々な問題) の答えが「存在する」だと分かる。大まかに言って、Menger の定理に含まれる命題はどれも「ある場所から別の場所へ向かう路からなる任意の二要素が独立した集合の最大要素数は、出発地点と到着地点を分離するボトルネックからなる集合の最小要素数に等しい」ことを主張する。ここで「場所」は頂点または頂点の集合を意味し、「独立した」は「共通の弧を持たない」または「共通の内部頂点を持たない」または「共通の頂点を一切持たない」を意味し、「ボトルネック」は「取り除くと出発地点と終着地点が切り離される弧の集合または頂点の集合」を意味する。本書で証明する Menger の定理を次の表にまとめる1:
-
有向グラフに関する命題:
\[ \def\arraystretch{1.33} \begin{array}{|c|c|c|c|}\hline \text{定理} & \text{「場所」} & \text{「独立」} & \text{「ボトルネック」} \\\hline\hline \href{/graph/more-about-path/mengers-theorem/#thm.menger.da1}{\text{定理 10.1.6}} & \text{頂点} & \text{弧素} & \text{弧} \\\hline \href{/graph/more-about-path/mengers-theorem/#thm.menger.da2}{\text{定理 10.1.10}} & \text{頂点} & \text{弧素} & \text{カットの弧}\\\hline \href{/graph/more-about-path/mengers-theorem/#thm.menger.dam}{\text{定理 10.1.18}} & \text{頂点の集合} & \text{弧素} & \text{カットの弧} \\\hline \href{/graph/more-about-path/mengers-theorem/#thm.menger.dv2}{\text{定理 10.1.32}} & \text{頂点} & \text{内部頂点素} & \text{頂点} \in V\setminus\left\{ s,t\right\} \\\hline \href{/graph/more-about-path/mengers-theorem/#thm.menger.dvm}{\text{定理 10.1.36}} & \text{頂点の集合} & \text{内部頂点素} & \text{頂点} \in V\setminus\left( X\cup Y\right) \\\hline \href{/graph/more-about-path/mengers-theorem/#thm.menger.dvm-vd}{\text{定理 10.1.39}} & \text{頂点の集合} & \text{頂点素} & \text{頂点} \in V\\\hline \end{array} \] -
無向グラフに関する命題:
\[ \def\arraystretch{1.33} \begin{array}{|c|c|c|c|}\hline \text{定理} & \text{「場所」} & \text{「独立」} & \text{「ボトルネック」}\\\hline\hline \href{/graph/more-about-path/mengers-theorem/#thm.menger.ue1}{\text{定理 10.1.22}} & \text{頂点} & \text{辺素} & \text{辺}\\\hline \href{/graph/more-about-path/mengers-theorem/#thm.menger.ue2}{\text{定理 10.1.25}} & \text{頂点} & \text{辺素} & \text{カットの辺}\\\hline \href{/graph/more-about-path/mengers-theorem/#thm.menger.uv2}{\text{定理 10.1.42}} & \text{頂点} & \text{内部頂点素} & \text{頂点} \in V\setminus\left\{ s,t\right\} \\\hline \href{/graph/more-about-path/mengers-theorem/#thm.menger.uvm}{\text{定理 10.1.44}} & \text{頂点の集合} & \text{内部頂点素} & \text{頂点} \in V\setminus\left( X\cup Y\right) \\\hline \href{/graph/more-about-path/mengers-theorem/#thm.menger.uvm-vd}{\text{定理 10.1.45}} & \text{頂点の集合} & \text{頂点素} & \text{頂点} \in V\\\hline \end{array} \]
10.1.1 有向グラフの弧に関する Menger の定理
最も自然な設定を最初に考える: 道路網は有向グラフで、道路は (一方向にだけ通行できる) 弧だとする。まず、定理の主張を短く表現するのに役立つ概念をいくつか定義する:
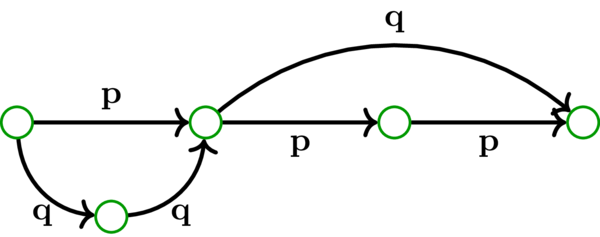
ある有向グラフにおける二つの歩道 \(\mathbf{p}\) と \(\mathbf{q}\) が共通の弧を持たないとき、\(\mathbf{p}\) と \(\mathbf{q}\) は弧素 (arc-disjoint) と言う。
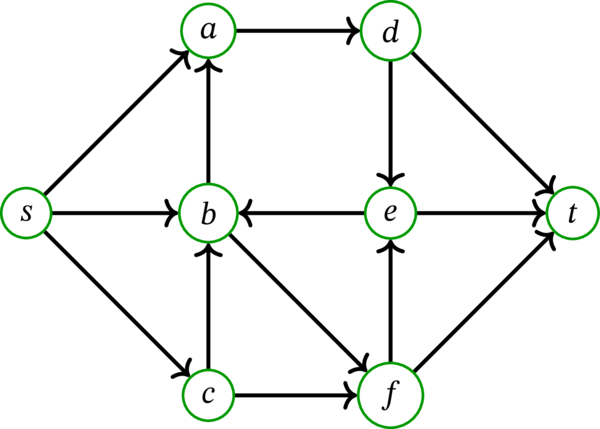
弧素な二つの路 \(\mathbf{p}\) と \(\mathbf{q}\) の例を次に示す。\(\mathbf{p}\) のラベルは \(\mathbf{p}\) に含まれる弧を表し、\(\mathbf{q}\) のラベルは \(\mathbf{q}\) に含まれる弧を表す:
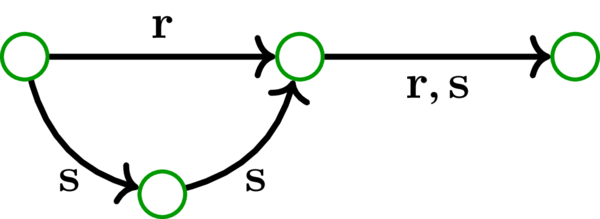
弧素でない二つの路 \(\mathbf{r}\) と \(\mathbf{s}\) の例を次に示す。「\(\mathbf{r},\mathbf{s}\)」のラベルは \(\mathbf{r}\) と \(\mathbf{s}\) に共通する弧を表す:
\(D=\left( V,A,\psi\right) \) を多重有向グラフ、\(s\) と \(t\) を \(D\) の異なる二頂点とする。\(A\) の部分集合 \(B\) が \(s\)-\(t\)-弧切断 (\(s\)-\(t\)-arc-separator) とは、\(s\) から \(t\) への任意の路が \(A\) に属する弧を含むことを意味する。言い換えれば、多重有向グラフ \(\left( V,\ A\setminus B,\ \psi|_{A\setminus B}\right) \) が \(s\) から \(t\) への路を持たないような \(A\) の部分集合 \(B\) を \(s\)-\(t\)-弧切断と呼ぶ。
\(D=\left( V,A,\psi\right) \) を次の多重有向グラフとする:
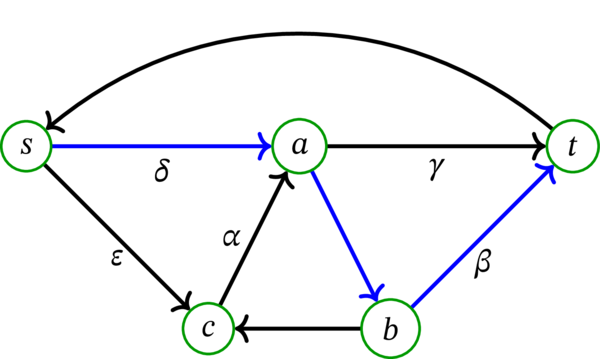
このとき、集合 \(\left\{ \alpha,\gamma\right\} \) は \(s\)-\(t\)-弧切断でない (青く示した \(s\) から \(t\) への路が存在するため)。これに対して、集合 \(\left\{ \beta,\gamma\right\} \) と \(\left\{ \delta,\varepsilon\right\} \) はどちらも \(s\)-\(t\)-弧切断である。当然、\(\left\{ \beta,\gamma\right\} \) または \(\left\{ \delta,\varepsilon\right\} \) を部分集合として含む任意の \(V\) の部分集合も \(s\)-\(t\)-弧切断となる。
\(D\) を多重有向グラフ、\(s\) と \(t\) を \(D\) の二頂点とする。このとき、空集合 \(\varnothing\) が \(s\)-\(t\)-弧切断となるのは \(D\) に \(s\) から \(t\) への路が存在しないとき、かつそのときに限る。この退化ケースを忘れるべきでない!
以上の定義を使えば、最初の Menger の定理を表明できる:
\(D=\left( V,A,\psi\right) \) を多重有向グラフ、\(s\) と \(t\) を \(D\) の異なる二頂点とする。このとき、\(D\) における \(s\) から \(t\) への路からなる任意の二要素が弧素な集合の最大要素数は、\(s\)-\(t\)-弧切断の最小要素数に等しい。
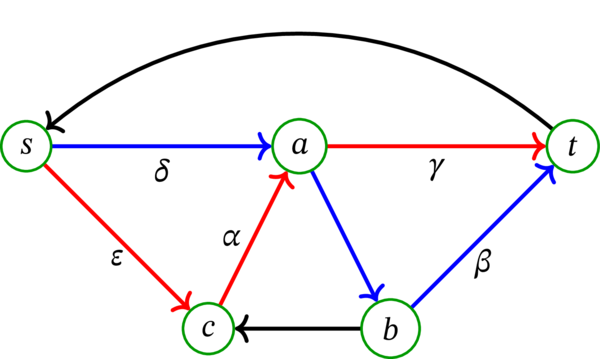
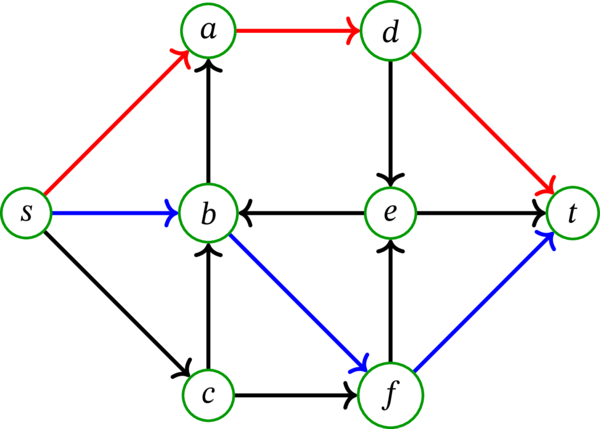
\(D\) を例 10.1.4 の多重有向グラフとする。このとき、\(s\)-\(t\)-弧切断の最小要素数は \(2\) である (実際、\(\left\{ \beta,\gamma\right\} \) が \(s\)-\(t\)-弧切断であり、要素数が \(1\) の \(s\)-\(t\)-弧切断が存在しないことは容易に分かる)。よって定理 10.1.6 より、\(s\) から \(t\) への路からなる任意の二要素が弧素な集合の最大要素数も \(2\) だと分かる。実際、\(s\) から \(t\) への弧素な二つの路は容易に見つけられる。具体的には次の図で青と赤で示された路である:
定理 10.1.6 を証明する前に、この定理の別バージョンを一つ表明する。こちらの方が証明される命題に近い。その別バージョンを表明するには、次の定義が必要になる:
\(D=\left( V,A,\psi\right) \) を多重有向グラフ、\(s\) と \(t\) を \(D\) の異なる二頂点とする。
-
\(V\) の任意の部分集合 \(S\) に対して、\(\overline {S}\) と \(\left[ S,\overline{S}\right]\) を次のように定める:
\[ \begin{aligned} \overline {S } &\colonequals V\setminus S \\ \left[ S,\overline{S}\right] &\colonequals \left\{ a\in A\mid (a \text{ の始点}) \in S \ \wedge \ (a \text{ の終点}) \in \overline{S} \right\} \end{aligned} \] -
\(s\)-\(t\)-カット (\(s\)-\(t\)-cut) とは、\(s\in S\) と \(t\notin S\) を満たす \(V\) の部分集合 \(S\) を使って \(\left[ S,\overline{S}\right] \) と表せる \(A\) の部分集合を意味する。
\(s\)-\(t\)-カットがこの名前で呼ばれるのは、\(s\)-\(t\)-カットに含まれる弧を除去すると \(s\) と \(t\) が切り離されるためである。正確に言えば、次の命題が成り立つ:
\(D=\left( V,A,\psi\right) \) を多重有向グラフ、\(s\) と \(t\) を \(D\) の異なる二頂点とする。このとき、任意の \(s\)-\(t\)-カットは \(s\)-\(t\)-弧切断である。
\(B\) を任意の \(s\)-\(t\)-カットとする。\(B\) が \(s\)-\(t\)-弧切断だと示せばよい。言い換えれば、\(s\) から \(t\) への任意の路が \(B\) に属する弧を少なくとも一つ含むと証明する必要がある。
\(B\) が \(s\)-\(t\)-カットだから、\(B=\left[ S,\overline {S}\right] \) と \(s\in S\) と \(t\notin S\) を満たす \(V\) の部分集合 \(S\) が存在する。この \(S\) に注目する。
\(s\) から \(t\) への任意の路を \(\mathbf{p}\) とする。\(s \in S\) より \(\mathbf{p}\) は \(S\) に属する頂点から始まり、\(s \notin S\) より \(\mathbf{p}\) は \(S\) に属さない頂点で終わる。よって、\(\mathbf{p}\) はどこかで \(S\) から脱出する ── つまり、\(S\) に属する始点と \(S\) に属さない終点を持つ弧を含む。ここから \(\mathbf{p}\) は \(\left[ S,\overline{S}\right] \) に属する辺を含むと分かる。\(B=\left[ S,\overline{S}\right] \) だから、\(s\) から \(t\) への任意の路 \(\mathbf{p}\) は \(B\) に属する辺を含む。言い換えれば、\(B\) は \(s\)-\(t\)-弧切断である (弧切断の定義より)。以上で Remark 10.1.9 は証明された。□
\(D=\left( V,A,\psi\right) \) を多重有向グラフ、\(s\) と \(t\) を \(D\) の異なる二頂点とする。このとき、\(D\) における \(s\) から \(t\) への路からなる任意の二要素が弧素な集合の最大要素数は、\(s\)-\(t\)-カットの最小要素数に等しい。
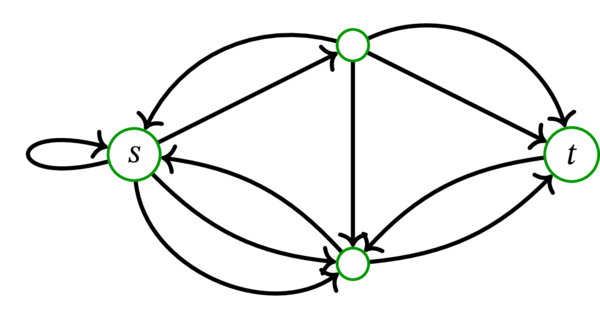
\(D\) を次の多重有向グラフとする:
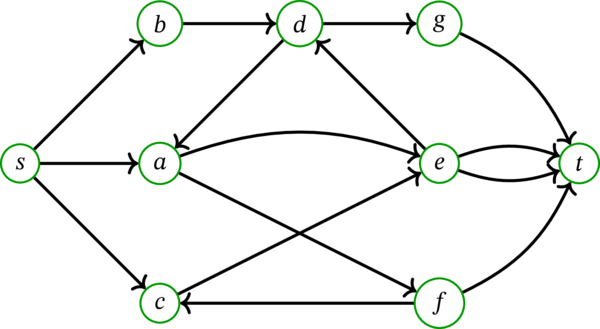
このとき、\(s\) から \(t\) への路からなる任意の二要素が弧素な集合の最大要素数は \(3\) である。実際、次の図に赤、青、茶で示した \(3\) つの路は任意の二つが弧素である:
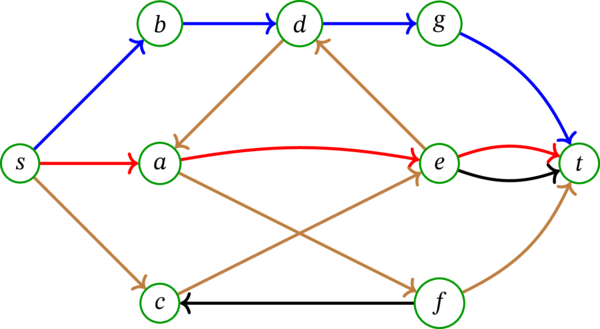
要素数が \(3\) より大きい \(s\) から \(t\) への路の集合は、弧素でない二つの路を必ず含む。なぜなら (例えば) \(s\) が外向き弧を \(3\) つしか持たないからである。
定理 10.1.10 によれば、\(D\) の \(s\)-\(t\)-カットの最小要素数も \(3\) に等しい。要素数 \(3\) の \(s\)-\(t\)-カットはいくつか存在する。例えば「明らかな」カット \(\left[ \left\{ s\right\},\, \overline{\left\{ s\right\} }\right] \) は要素数 \(3\) の \(s\)-\(t\)-カットであり、\(\left[ \left\{ s,a,f\right\},\, \overline{\left\{ s,a,f\right\} }\right] \) も要素数 \(3\) の \(s\)-\(t\)-カットである。
\(D\) の \(c\) から \(e\) への弧の向きを反転させたグラフを考える (このとき茶色の路が無効になる)。このグラフ \(D^{\prime}\) を示す:
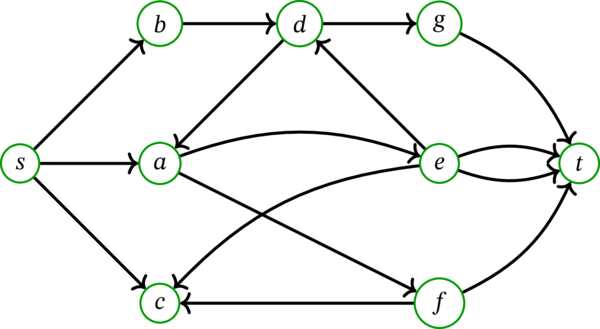
この有向グラフ \(D^{\prime}\) では、\(s\) から \(t\) への路からなる任意の二要素が弧素な集合の最大要素数は \(2\) である。実際、\(s\)-\(t\)-カット \(\left[ \left\{ s,c\right\},\, \overline{\left\{ s,c\right\} }\right] \) (\(s\) から \(t\) への弧と \(s\) から \(b\) への弧からなる) の要素数が \(2\) なので、\(s\)-\(t\)-カットの最小要素数は \(2\) 以下であり、定理 10.1.10 より \(s\) から \(t\) への路からなる任意の二要素が弧素な集合の最大要素数も \(2\) 以下と分かる。後者の値がちょうど \(2\) であることは容易に分かる (赤色の路と青色の路は \(D^{\prime}\) にも存在する)。
これまでに表明した二つの Menger の定理を証明するには、ネットワークに関する補題を一つ証明する必要がある。第 9.1 節の定義と定義 9.4.1 を思い出した上で、さらに記法を定義する:
\(D=\left( V,A,\psi\right) \) を多重有向グラフ、\(f,g\colon A\rightarrow \mathbb{N}\) を二つの写像とする。このとき:
-
任意の弧 \(a \in A\) を \(f\left( a\right) +g\left( a\right) \) に移す \(A\) から \(\mathbb{N}\) への写像を \(f + g\) と表記する。
-
任意の弧 \(a \in A\) が \(g\left( a\right) \leq f\left( a\right) \) を満たすとき、かつそのときに限って \(g\leq f\) と書く。
-
もし \(g\leq f\) なら、任意の弧 \(a \in A\) を \(f\left( a\right) -g\left( a\right) \) に移す \(A\) から \(\mathbb{N}\) への写像を \(f - g\) と表記する (この写像の値域が \(\mathbb{N}\) であることは、\(g\leq f\) が任意の弧 \(a\in A\) に対して \(g\left( a\right) \leq f\left( a\right) \) を意味することから分かる)。
これらの記法は自然に期待される性質を持つ: 例えば \(A\) から \(\mathbb{N}\) への写像の点ごとの和は結合性を持つ。つまり、写像としての等式 \(\left( f+g\right) +h=f+\left( g+h\right) \) が成り立つので、両者を \(f + g + h\) と書ける。また、不等式を通常通りに変形することもできる。例えば \(f-g\leq h\) が成り立つのは \(f \leq g + h\) が成り立つとき、かつそのときに限る。これらの命題はどれも簡単に確かめられる。
次の定義は Remark 9.1.8 で考えたフローを形式的に成文化したものである:
多重有向グラフ \(D=\left( V,A,\psi\right) \)、入口 \(s \in V\)、出口 \(t \in V\)、容量関数 \(c\colon A\rightarrow\mathbb{N}\) から構成されるネットワークを \(N\) とする。\(D\) における \(s\) から \(t\) への任意の路 \(\mathbf{p}\) に対して、写像 \(f_{\mathbf{p}}\colon A\rightarrow \mathbb{N}\) を次のように定める:
この写像 \(f_{\mathbf{p}}\) を \(\mathbf{p}\) の路フロー (path flow) と呼ぶ。\(\mathbf{p}\) の弧が全て \(1\) 以上の容量を持つなら、\(\mathbf{p}\) の路フロー \(f_{\mathbf{p}}\)は実際に値 \(1\) のフローとなる。
次のネットワークを考える:
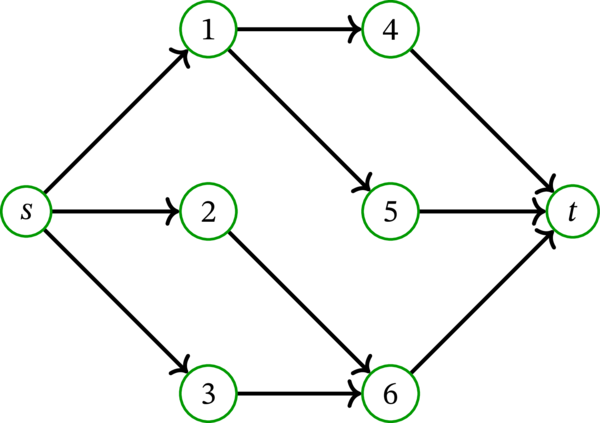
全ての弧の容量は \(1\) とする。このとき、路 \(\mathbf{p}=\left( s,2,6,t\right) \) からは次の路フロー \(f_{\mathbf{p}}\) が得られる:
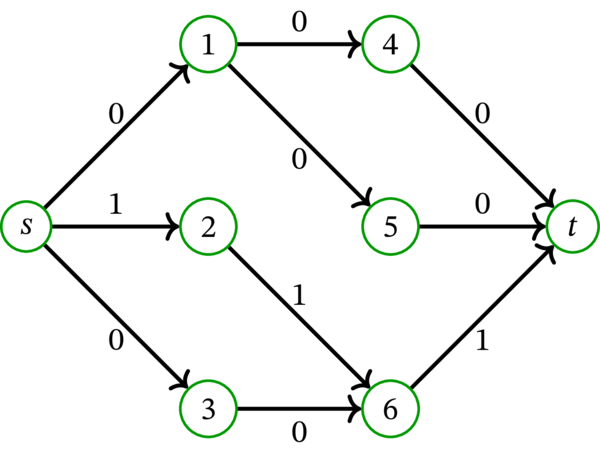
図を簡潔するにするため、弧のラベルには「of \(1\)」を書いていない。そのため弧に付いているラベル「\(1\)」は「\(1\) of \(1\)」と、「\(0\)」は「\(0\) of \(1\)」と解釈するべきである。
つまりネットワークにおける \(s\) から \(t\) への路に含まれる全ての弧が十分な容量を持っていれば、その路は路フローというフローに変換できる。もし \(s\) から \(t\) への \(m\) 個の路 \(\mathbf{p}_{1}\), \(\mathbf{p}_{2}\), ..., \(\mathbf{p}_{m}\) が存在して対応する弧が十分な容量を持っていれば、値 \(m\) のフロー \(f_{\mathbf{p}_{1}}+f_{\mathbf{p}_{2}}+\cdots+f_{\mathbf{p}_{m}}\) が得られる (一般に、後者のフローから \(\mathbf{p}_{1}\), \(\mathbf{p}_{2}\), ..., \(\mathbf{p}_{m}\) を一意に復元することはできない: フローが「混じり合って」識別不可能になる可能性がある)。
この観察の (ほぼ) 逆を示すのが次の補題である: 値が \(m\) の任意のフロー \(f\) は、\(m\) 個の (必ずしも相異なるとは限らない) \(s\) から \(t\) への路 \(\mathbf{p}_{1}\), \(\mathbf{p}_{2}\), ..., \(\mathbf{p}_{m}\) に対応する \(m\) 個の路フロー \(f_{\mathbf{p}_{1}}\), \(f_{\mathbf{p}_{2}}\), ..., \(f_{\mathbf{p}_{m}}\) の和 \(f_{\mathbf{p}_{1}}+f_{\mathbf{p}_{2}}+\cdots+f_{\mathbf{p}_{m}}\) を含む。ここで「含む」とは \(f\) が \(f_{\mathbf{p}_{1}}+f_{\mathbf{p}_{2}}+\cdots +f_{\mathbf{p}_{m}}\) に等しいことではなく、不等式 \(f_{\mathbf{p}_{1}}+f_{\mathbf{p}_{2}}+\cdots+f_{\mathbf{p}_{m}}\leq f\) が成り立つことを意味する。この補題は次の通りである:
多重有向グラフ \(D=\left( V,A,\psi\right) \)、入口 \(s \in V\)、出口 \(t \in V\)、容量関数 \(c\colon A\rightarrow\mathbb{N}\) から構成されるネットワークを \(N\) とする。値 \(m\) を持つ \(N\) 上の任意のフローを \(f\) とする。このとき、次の条件を満たす \(s\) から \(t\) への \(m\) 個の路 \(\mathbf{p}_{1}\), \(\mathbf{p}_{2}\), ..., \(\mathbf{p}_{m}\) が \(D\) に存在する:
\(m\) に関する数学的帰納法で示す。
ベースケース: \(m = 0\) のとき主張は明らかである (和 \(f_{\mathbf{p}_{1}}+f_{\mathbf{p}_{2}}+\cdots+f_{\mathbf{p}_{m}}\) は零フローなので、容量制約から従う)。
再帰ステップ: \(m\) を正整数とする。\(m=m-1\) の場合に補題が成り立つと (帰納法の仮定として) 仮定する。これから \(m=m\) の場合に補題が成り立つことを証明する。
値 \(m\) を持つ \(N\) 上のフロー \(f\) を考える。\(f_{\mathbf{p}_{1}}+f_{\mathbf{p}_{2}}+\cdots+f_{\mathbf{p}_{m}}\leq f\) を満たす \(s\) から \(t\) への \(m\) 個の路 \(\mathbf{p}_{1}\), \(\mathbf{p}_{2}\), ..., \(\mathbf{p}_{m}\) が \(D\) に存在すると示せばよい。
最初に \(f_{\mathbf{p}}\leq f\) を満たす \(s\) から \(t\) への路 \(\mathbf{p}\) が \(D\) に存在することを示す。
\(A^{\prime}\colonequals \left\{ a\in A\mid f\left( a\right) >0\right\} \) と定め、\(D\) の全域部分有向グラフ \(D^{\prime}\colonequals \left( V,A^{\prime},\psi|_{A^{\prime}}\right) \) を考える。\(D^{\prime}\) に \(s\) から \(v\) への路が存在するような頂点 \(v \in V\) 全体の集合を \(S\) とする。このとき \(s \in S\) である (自明な路 \(\left( s\right) \) は \(D^{\prime}\) における \(s\) から \(s\) への路であるため)。
これから任意の弧 \(b\in\left[ S,\overline{S}\right] \) が \(f\left( b\right) =0\) を満たすことを示す。
[証明: 背理法で示す。ある弧 \(b\in\left[ S,\overline{S}\right] \) が \(f\left( b\right) \neq0\) を満たすと仮定する。この \(b\) に注目する。\(f\) はフローだから、フローの容量制約と \(f\left( b\right) \neq0\) より \(f\left( b\right) >0\) を得る。よって \(A^{\prime}\) の定義から \(b \in A^{\prime}\) を得る。ここから \(D^{\prime}\) の定義より \(b\) は \(D^{\prime}\) の弧だと分かる。
\(u\) を弧 \(b\) の始点、\(v\) を弧 \(b\) の終点とする。\(b\in\left[ S,\overline{S}\right] \) より \(u\in S\) と \(v \in \overline{S}\) が分かる。\(u \in S\) より、有向グラフ \(D^{\prime}\) には \(s\) から \(u\) への路 \(\mathbf{p}\) が存在する。この \(\mathbf{p}\) に注目する。路 \(\mathbf{p}\) の末尾に弧 \(b\) と頂点 \(v\) を付け足すと、\(D^{\prime}\) における \(s\) から \(v\) への歩道が得られる (\(b\) は \(D^{\prime}\) の弧であり、始点 \(u\) と終点 \(v\) を持つため)。よって有向グラフ \(D^{\prime}\) は \(s\) から \(v\) への歩道を持ち、命題 4.5.8 より \(s\) から \(v\) への路も持つ。よって \(S\) の定義より \(v \in S\) が言える。しかしこれは \(v\in\overline{S}=V\setminus S\) と矛盾する。この矛盾から仮定が偽だと分かる。これで示したい命題は証明された。]
任意の弧 \(b\in\left[ S,\overline{S}\right] \) が \(f\left( b\right) =0\) を満たすと分かった。つまり \(f\left( S,\overline{S}\right) =0\) が成り立つ (定義 9.1.5 (d) で定めた記法を使っている)。一方 \(s \in S\) だから、もし \(t \notin S\) なら 命題 9.3.2 (b) より次の等式が成り立つ:
しかし、これは \(\left\vert f\right\vert =m>0\) と矛盾する。つまり \(t \in S\) である。\(S\) の定義を使って言い換えれば、\(D^{\prime}\) には \(s\) から \(t\) への路 \(\mathbf{p}\) が存在する。この路 \(\mathbf{p}\) は \(D\) の路でもあり、\(f_{\mathbf{p}}\leq f\) を満たす2。よって \(f-f_{\mathbf{p}}\) は \(A\) から \(\mathbb{N}\) への写像である。さらに \(f-f_{\mathbf{p}}\) もフローであり3、その値は \(\left\vert f-f_{\mathbf{p}}\right\vert =m-1\) を満たす4。よって帰納法の仮定より、\(s\) から \(t\) への \(m-1\) 個の路 \(\mathbf{p}_{1}\), \(\mathbf{p}_{2}\), ..., \(\mathbf{p}_{m-1}\) であって \(f_{\mathbf{p}_{1}}+f_{\mathbf{p}_{2}}+\cdots+f_{\mathbf{p}_{m-1}}\leq f-f_{\mathbf{p}}\) を満たすものが \(D\) に存在する。\(\mathbf{p}_{m}\colonequals \mathbf{p}\) と定めれば \(f_{\mathbf{p}_{1}}+f_{\mathbf{p}_{2}}+\cdots+f_{\mathbf{p}_{m-1}}\leq f-f_{\mathbf{p}}=f-f_{\mathbf{p}_{m}}\) であり、ここから \(f_{\mathbf{p}_{1}}+f_{\mathbf{p}_{2}}+\cdots+f_{\mathbf{p}_{m}}\leq f\) を得る。
\(f_{\mathbf{p}_{1}}+f_{\mathbf{p}_{2}}+\cdots+f_{\mathbf{p}_{m}}\leq f\) を満たす \(s\) から \(t\) への \(m\) 個の路 \(\mathbf{p}_{1}\), \(\mathbf{p}_{2}\), ..., \(\mathbf{p}_{m}\) が \(D\) に存在すると分かったので、帰納ステップは完了した。以上で補題 10.1.15 は証明された。□
補題 10.1.15 には別証明がある。非常に簡潔で言及しないのは惜しいので、ここに概略を示す: \(D\) の各弧 \(a\) を \(f\left( a\right) \) 個の平行辺に置き換えて得られる多重有向グラフを考える (\(f\left( a\right) = 0\) を満たす弧 \(a\) は除去される)。この新しい多重有向グラフに始点 \(t\) と終点 \(s\) を持つ弧を \(m\) 本追加する。こうして得られる多重有向グラフは平衡である (フローの保存制約より)。弱連結とは限らないものの、頂点 \(s\), \(t\) は (\(m > 0\) なら) 同じ弱成分に属する。よって \(s\) と \(t\) が属する弱成分に Euler–Hierholzer の定理 (定理 4.7.2) を適用すると、この弱成分がオイラー回路を持つことが分かる。このオイラー回路から始点 \(s\) と終点 \(t\) を持つ \(m\) 本の弧を除去すると、\(s\) から \(t\) への \(m\) 個の弧素な歩道が得られる。この \(m\) 個の歩道はそれぞれ \(s\) から \(t\) への路を含むので、それらを \(\mathbf{p}_{1}\), \(\mathbf{p}_{2}\), ..., \(\mathbf{p}_{m}\) とすれば \(f_{\mathbf{p}_{1}}+f_{\mathbf{p}_{2}}+\cdots +f_{\mathbf{p}_{m}}\leq f\) が成り立つ。
多重有向グラフ \(D=\left( V,A,\psi\right) \)、入口 \(s \in V\)、出口 \(t \in V\)、そして容量関数 \(c\colon A\rightarrow\mathbb{N}\) から構成されるネットワークを \(N\) とする。\(D\) の閉路 \(\mathbf{c}\) に対して、次のように写像 \(f_{\mathbf{c}}\colon A\rightarrow\mathbb{N}\) を定める:
この写像を使うと、補題 10.1.15 の結論を次のように改善できる: 次の条件を満たす \(s\) から \(t\) への \(m\) 個の路 \(\mathbf{p}_{1}\), \(\mathbf{p}_{2}\), ..., \(\mathbf{p}_{m}\) と、いくつかの (\(0\) 個でもあり得る) 閉路 \(\mathbf{c}_{1}\), \(\mathbf{c}_{2}\), ..., \(\mathbf{c}_{k}\) が \(D\) に存在する:
この改善された命題の証明は補題 10.1.15 より少し難しいものの、非常に難しいわけではない (特に、歩道に含まれる閉路を除去すると路となる事実を利用すれば、Remark 10.1.16 と同じ議論が利用できる)。
\(D\) の全ての弧に容量 \(1\) を割り当てることで、入口 \(s\) と出口 \(t\) を持つネットワーク \(N\) を構成する。明らかに、このネットワーク \(N\) のカットは \(D\) の \(s\)-\(t\)-カットに等しい。さらに、全ての弧の容量が \(1\) なので、\(N\) のカット \(\left[ S,\overline{S}\right] \) の容量 \(c\left( S,\overline{S}\right) \) は \(\left[ S,\overline{S}\right] \) の要素数に等しい。
最大フロー最小カット定理 (定理 9.4.3) によれば、フローの値の最大値はカットの容量の最小値に等しい。よって前段落の議論より、\(N\) 上のフローの値の最大値は \(D\) の \(s\)-\(t\)-カットの最小要素数に等しい。後は、\(s\) から \(t\) への路からなる任意の二要素が弧素な集合の最大要素数がフローの値の最大値だと示せばよい。しかし、ここまでに示してきた命題を使えばこの証明は難しくない:
-
値が \(m\) のフロー \(f\) からは、どの二つも弧素な \(s\) から \(t\) への \(m\) 個の路が得られる (補題 10.1.15 より \(f_{\mathbf{p}_{1}}+f_{\mathbf{p}_{2}}+\cdots+f_{\mathbf{p}_{m}}\leq f\) を満たす \(s\) から \(t\) への \(m\) 個の路 \(\mathbf{p}_{1}\), \(\mathbf{p}_{2}\), ..., \(\mathbf{p}_{m}\) の存在が分かる。この不等式より、これらの \(m\) 個の路の任意の二つは弧素だと分かる5)。よって次の不等式を得る:
\[ \begin{aligned} & \left(s \text{ から } t \text{ への路からなる任意の二要素が弧素な集合の最大要素数}\right) \\ & \quad \geq\left( \text{フローの値の最大値}\right) \end{aligned} \] -
逆に、もし \(s\) から \(t\) への \(m\) 個の路 \(\mathbf{p}_{1}\), \(\mathbf{p}_{2}\), ..., \(\mathbf{p}_{m}\) の任意の二要素が弧素なら、値が \(m\) のフローを構築できる (具体的には \(f_{\mathbf{p}_{1}}+f_{\mathbf{p}_{2}}+\cdots+f_{\mathbf{p}_{m}}\) がそのようなフローである6)。よって次の不等式を得る:
\[ \begin{aligned} & \left( \text{フローの値の最大値}\right) \\ & \quad \geq\left( s \text{ から } t \text{ への路からなる任意の二要素が弧素な集合の最大要素数} \right) \end{aligned} \]
二つの不等式から次の等式を得る:
以上で定理 10.1.10 は証明された。□
ネットワークとフローを使わない定理 10.1.10 の証明も知られている。[Schrij17, Corollary 4.1b] などを参照してほしい。
\(s\) から \(t\) への路からなる任意の二要素が弧素な集合の最大要素数を \(x\)、\(s\)-\(t\)-カットの最小要素数を \(n_{c}\)、\(s\)-\(t\)-弧切断の最小要素数を \(n_{s}\) とする7。
定理 10.1.10 より \(x = n_{c}\) を得る。ここでの目標は \(x=n_{s}\) の証明である。
Remark 10.1.9 より、任意の \(s\)-\(t\)-カットは \(s\)-\(t\)-弧切断である。よって \(n_{s}\leq n_{c}\) が分かる。また、\(x\leq n_{s}\) は鳩の巣原理から容易に分かる8。二つの不等式と \(x = n_{c}\) より \(x = n_{s}\) を得る。以上で定理 10.1.6 は証明された。□
\(D\) を平衡な多重有向グラフ、\(s\) と \(t\) を \(D\) の異なる二頂点、\(k\) を自然数とする。任意の二つが弧素な \(s\) から \(t\) への \(k\) 個の路が \(D\) に存在すると仮定する。このとき、任意の二つが弧素な \(t\) から \(s\) への \(k\) 個の路が存在すると示せ。
\(D\) を多重有向グラフ、\(k\) を自然数、\(u\), \(v\), \(w\) を \(D\) の三頂点とする。任意の二つが弧素な \(u\) から \(v\) への \(k\) 個の路が \(D\) に存在すると仮定する。さらに、任意の二つが弧素な \(v\) から \(w\) への \(k\) 個の路が \(D\) に存在すると仮定する。
任意の二つが弧素な \(u\) から \(w\) への \(k\) 個の路が \(D\) に存在することを示せ。
弧に関する Menger の定理は頂点の集合の組に関する命題に拡張できる:
\(D=\left( V,A,\psi\right) \) を多重有向グラフとする。共通要素を持たない二つの \(V\) の部分集合を \(X\), \(Y\) とする。
\(X\) から \(Y\) への路 (path from \(X\) to \(Y\)) とは、始点が \(X\) に属し、終点が \(Y\) に属する \(D\) の路を言う。
\(X\)-\(Y\)-カット (\(X\)-\(Y\)-cut) とは、\(X\subseteq S\) と \(Y\subseteq\overline{S}\) を満たす \(V\) の部分集合 \(S\) を使って \(\left[ S,\overline{S}\right] \) と書ける \(A\) の部分集合を言う。
このとき、\(X\) から \(Y\) への路からなる任意の二要素が弧素な集合の最大要素数と \(X\)-\(Y\)-カットの最小要素数は一致する。
有向グラフ \(D=\left( V,A,\psi\right) \) と共通要素を持たない \(V\) の部分集合 \(X\), \(Y\) の例を次に示す:
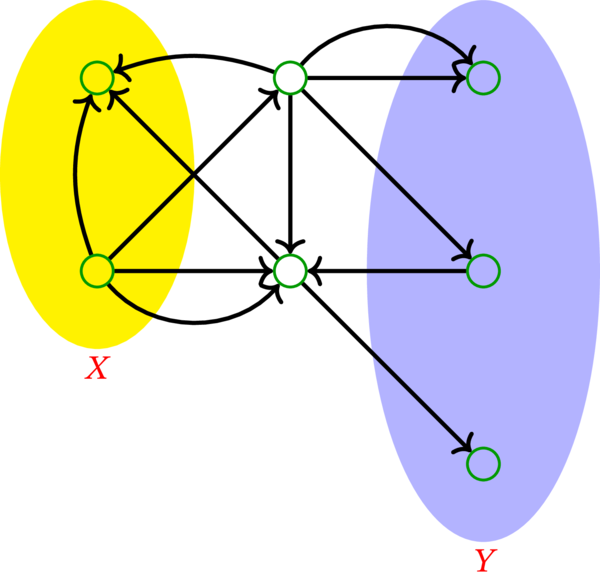
この有向グラフ \(D\) において、\(X\) から \(Y\) への路からなる任意の二要素が弧素な集合の最大要素数は \(2\) である。\(D\) が持つ弧素な二つの路を次の図に (赤と青で) 示す:
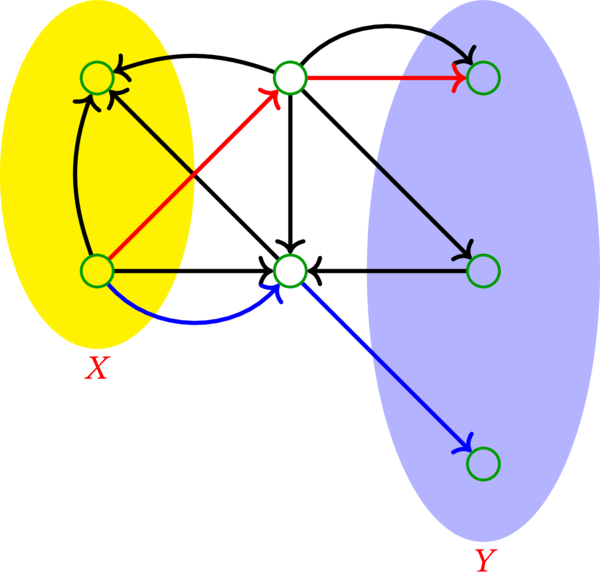
定理 10.1.18 は \(X\)-\(Y\)-カットの最小要素数も \(2\) だと主張する。実際、要素数が \(2\) の \(X\)-\(Y\)-カットは存在する:
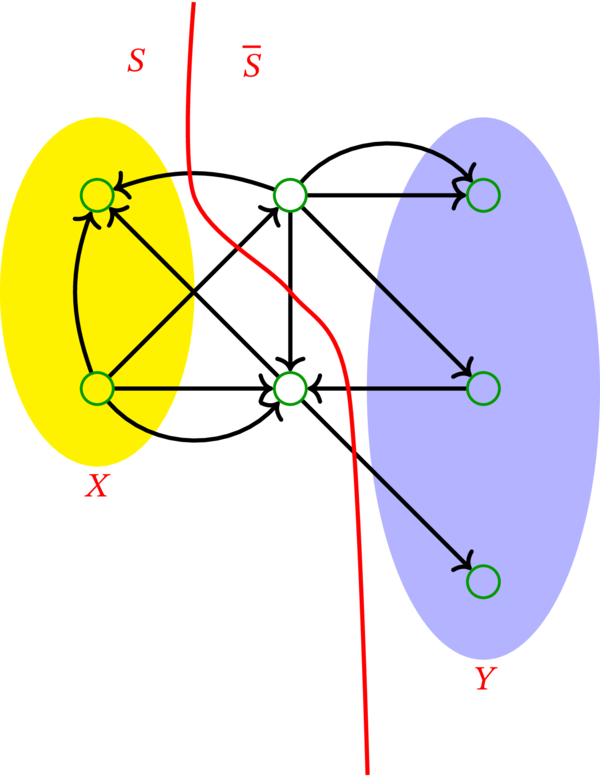
与えられた多重有向グラフ \(D=\left( V,A,\psi\right) \) を次の手順で改変し、新しい多重有向グラフ \(D^{\prime}=\left( V^{\prime },A^{\prime},\psi^{\prime}\right) \) を定義する:
-
\(X\) に属する全ての頂点を一つの (新しい) 頂点 \(s\) に置き換え、\(Y\) に属する全ての頂点を一つの (新しい) 頂点 \(t\) に置き換える。形式的に表現すれば、\(V^{\prime} \colonequals \left( V\setminus\left( X\cup Y\right) \right) \cup\left\{ s,t\right\} \) と定める。ここで \(s\) と \(t\) は \(V\) に属さない新しいオブジェクトを表す。
任意の頂点 \(p \in V\) に対して、頂点 \(p^{\prime}\in V^{\prime}\) を次のように定める:
\[ p^{\prime}= \begin{cases} s & (p\in X \text{ のとき})\\ t & (p\in Y \text{ のとき})\\ p & (\text{それ以外のとき}) \end{cases} \]この頂点 \(p^{\prime}\) を \(p\) の射影 (projection) と呼ぶ。
-
\(D\) の弧は全てそのままとする。ただし、弧の端点 (始点と終点) はその射影で置き換える (つまり、\(X\) に属する端点は \(s\) で置き換え、\(Y\) に属する端点は \(t\) で置き換え、\(X\) にも \(Y\) にも属さない端点はそのままとする)。例えば、\(X\) に属する始点を持つ弧は \(s\) を始点に持つ弧になる。形式的に表現すると次のようになる: \(A^{\prime}=A\) と定め、\(\psi^{\prime}\colon A^{\prime}\rightarrow V^{\prime}\times V^{\prime}\) を次のように定める: 任意の \(a \in A^{\prime}=A\) に対して \(\left( u,v\right) =\psi\left( a\right) \) を満たす \(u\), \(v\) を用いて \(\psi^{\prime}\left( a\right) =\left( u^{\prime},v^{\prime}\right) \) と定める。
例えば、例 10.1.19 の多重有向グラフを \(D\) とするとき、\(D^{\prime}\) は次の多重有向グラフとなる:
定理 10.1.10 を \(D^{\prime}=\left( V^{\prime },A^{\prime},\psi^{\prime}\right) \) に適用すると、\(D^{\prime}\) における \(s\) から \(t\) への路からなる任意の二要素が弧素な集合の最大要素数が \(D^{\prime}\) の \(s\)-\(t\)-カットの最小要素数に等しいと分かる。
この事実を使って示すべき命題を証明しよう。\(D^{\prime}\) の \(s\)-\(t\)-カットの最小要素数が \(D\) の \(X\)-\(Y\)-カットの最小要素数に等しいことは容易に分かる (実際、\(D^{\prime}\) の \(s\)-\(t\)-カットは \(D\) の \(X\)-\(Y\)-カットでもある9)。\(D^{\prime}\) における \(s\) から \(t\) への路からなる任意の二要素が弧素な集合の最大要素数が \(D\) における \(X\) から \(Y\) への路からなる任意の二要素が弧素な集合の最大要素数と等しいと示せれば、前段落の事実から定理 10.1.18 が証明される。
では、\(D^{\prime}\) における \(s\) から \(t\) への路からなる任意の二要素が弧素な集合の最大要素数が \(D\) における \(X\) から \(Y\) への路からなる任意の二要素が弧素な集合の最大要素数と等しいと示すには、どうすればいいだろうか? 二つの集合の間に全単射があればすぐに示せるものの、全単射の存在は自明でない: \(D^{\prime}\) の同じ頂点に射影される \(D\) の頂点が存在するので、\(D\) における \(X\) から \(Y\) への路に含まれる頂点をその射影に置き換えると、得られるのは \(D^{\prime}\) における \(s\) から \(t\) への歩道となる。
幸い、これは簡単に修正できる。\(D\) における \(X\) から \(Y\) への路からなる任意の二要素が弧素な \(k\) 要素集合が存在すると仮定する。このとき、それぞれの路に含まれる頂点をその射影と置き換えることで、\(D^{\prime}\) における \(s\) から \(t\) への歩道からなる任意の二要素が弧素な \(k\) 要素集合を構築できる。さらに、その集合に含まれる歩道をそれが含む路に置き換えると、\(s\) から \(t\) への路からなる任意の二要素が弧素な \(k\) 要素集合が得られる (命題 4.5.8 の証明から分かるように、任意の \(s\) から \(t\) への歩道は \(s\) から \(t\) への路を含む)。よって次の不等式を得る:
逆に、\(D^{\prime}\) における \(s\) から \(t\) への路からなる任意の二要素が弧素な \(k\) 要素集合が存在すると仮定する。この集合に含まれる \(k\) 個の路を\(D\) の路に「引き上げる」(弧はそのままにして、頂点 \(s\), \(t\) をそれぞれ弧と矛盾しない \(X\), \(Y\) に属する頂点に置き換える) ことで、\(D\) における \(X\) から \(Y\) への路からなる任意の二要素が弧素な \(k\) 要素集合が得られる。よって次の不等式を得る:
二つの不等式より次の等式が分かる:
先述したように、これで定理 10.1.18 は証明された。□
10.1.2 無向グラフの辺に関する Menger の定理
これから定理 10.1.6 と定理 10.1.10 の無向グラフバージョンと言える命題を示す。面白くない定義が最初にある:
ある無向グラフにおける歩道 \(\mathbf{p}\) と \(\mathbf{q}\) が共通の辺を持たないとき、\(\mathbf{p}\) と \(\mathbf{q}\) は辺素 (edge-disjoint) と言う。
\(G=\left( V,E,\varphi\right) \) を多重グラフ、\(s\) と \(t\) を \(G\) の異なる二頂点とする。\(E\) の部分集合 \(B\) が \(s\)-\(t\)-辺切断 (\(s\)-\(t\)-edge-separator) とは、\(s\) から \(t\) への任意の路が \(B\) に属する辺を少なくとも一つ含むことを意味する。言い換えれば、多重グラフ \(\left( V,\ E\setminus B,\ \varphi|_{E\setminus B}\right) \) が \(s\) から \(t\) への路を持たないような \(E\) の部分集合 \(B\) を \(s\)-\(t\)-辺切断と呼ぶ。
定理 10.1.6 には次の命題が対応する:
\(G=\left( V,E,\varphi\right) \) を多重グラフ、\(s\) と \(t\) を \(G\) の異なる二頂点とする。このとき、\(G\) における \(s\) から \(t\) への路からなる任意の二要素が辺素な集合の最大要素数は、\(s\)-\(t\)-辺切断の最小要素数に等しい。
定理 10.1.10 の無向グラフバージョンを表明するには、定義 10.1.8 に対応する次の定義が必要になる:
\(G=\left( V,E,\varphi\right) \) を多重グラフ、\(s\) と \(t\) を \(G\) の異なる二頂点とする。
-
\(V\) の任意の部分集合 \(S\) に対して、\(\overline{S}\) と \([S,\overline{S}]_{\operatorname*{und}}\) を次のように定める:
\[ \begin{aligned} \overline{S} &\colonequals V \setminus S \\ \left[ S,\overline{S}\right] _{\operatorname*{und}} & \colonequals \{ e\in E\mid e\text{ の端点の一つが } S \text{ に属し、} \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{もう一方の端点が } \overline{S} \text{ に属する} \} \end{aligned} \] -
無向 \(s\)-\(t\)-カット (undirected \(s\)-\(t\)-cut) とは、\(s\in S\) と \(t\notin S\) を満たす \(V\) の部分集合 \(S\) を使って \(\left[ S,\overline{S}\right]_{\operatorname*{und}} \) と表せる \(A\) の部分集合を意味する。無向 \(s\)-\(t\)-カットは単に \(s\)-\(t\)-カットとも呼ぶ。
次の Remark は Remark 10.1.9 に対応する:
\(G=\left( V,E,\varphi\right) \) を多重グラフ、\(s\) と \(t\) を \(G\) の異なる二頂点とする。このとき、任意の無向 \(s\)-\(t\)-カットは \(s\)-\(t\)-辺切断である。
Remark 10.1.9 と同様に示せる。□
次の定理は定理 10.1.10 の無向グラフバージョンである:
\(G=\left( V,E,\varphi\right) \) を多重グラフ、\(s\) と \(t\) を \(G\) の異なる二頂点とする。このとき、\(s\) から \(t\) への路からなる任意の二要素が辺素な集合の最大要素数は、無向 \(s\)-\(t\)-カットの最小要素数に等しい。
何もないところから証明を組み立てることはせず、有向グラフに対する同様の命題 (定理 10.1.10) を使って証明する。
具体的には、定理 10.1.10 を \(D=G^{\operatorname*{bidir}}\) に適用する10。ここから、\(G^{\operatorname*{bidir}}\) における \(s\) から \(t\) への路からなる任意の二要素が弧素な集合の最大要素数は、\(G^{\operatorname*{bidir}}\) の \(s\)-\(t\)-カットの最小要素数に等しいと分かる。 これは示したい命題に似ているものの、同じではない: \(G^{\operatorname*{bidir}}\) と \(G\) は異なる。示したい命題を得るには、次の二つの命題を証明する必要がある:
Claim 2: \(G^{\operatorname*{bidir}}\) の有向 \(s\)-\(t\)-カット11の最小要素数は、\(G\) の無向 \(s\)-\(t\)-カットの最小要素数に等しい。
Claim 2 は簡単に確かめられる: \(G^{\operatorname*{bidir}}\) の有向 \(s\)-\(t\)-カットは \(G\) の無向 \(s\)-\(t\)-カットに本質的に等しい12。
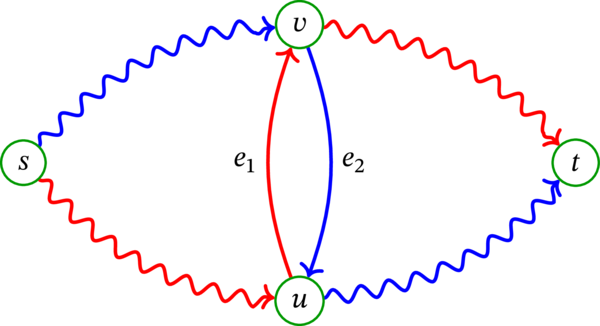
後は Claim 1 を確かめればよい。最も単純なアプローチは \(G^{\operatorname*{bidir}}\) における \(s\) から \(t\) への路を (路に含まれる弧を対応する無向辺に置き換えることで) \(G\) における \(s\) から \(t\) への路に変換できると論じるものである。しかし、この議論は正しくない: この変換方法では、\(G^{\operatorname*{bidir}}\) で弧素な二つの路から得られる \(G\) における二つの路が辺素にならない可能性がある。この例を次に示す。\(u\) と \(v\) の間にある二つの弧は \(G\) で一つの辺となるものの、\(G^{\operatorname*{bidir}}\) では赤と青の二つの路によって利用されている:
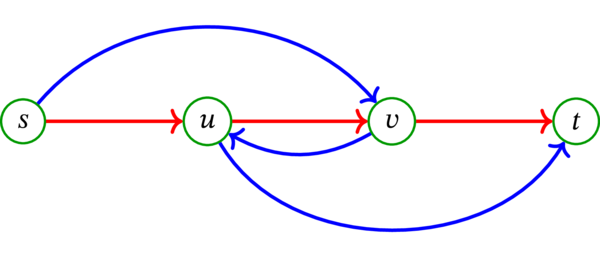
この図で赤と青が表す二つの路に含まれる弧を辺に置き換えると、辺素でない二つの路が得られる (\(u\) と \(v\) を端点に持つ辺が両方の路によって使われるため)。
しかし、この種の状況を回避する方法がある。\(G^{\operatorname*{bidir}}\) における \(s\) から \(t\) への路からなる任意の二要素が弧素な集合の最大要素数を \(k\) とする。その上で、\(G^{\operatorname*{bidir}}\) における \(s\) から \(t\) への路からなる任意の二要素が弧素な \(k\) 要素集合 \(\{\mathbf{p}_{1},\mathbf{p}_{2},\ldots,\mathbf{p}_{k}\}\) を、全長が最小になるように取る (路の集合の全長とは \(\mathbf{p}_{1},\mathbf{p}_{2},\ldots ,\mathbf{p}_{k}\) の長さの和を意味する)。このとき、\(\mathbf{p}_{1},\mathbf{p}_{2},\ldots,\mathbf{p}_{k}\) の弧を辺に置き換えて得られる \(k\) 個の \(G\) における路は任意の二つが辺素となることが容易に示せる。
[証明: 背理法で示す。\(\mathbf{p}_{1},\mathbf{p}_{2},\ldots,\mathbf{p}_{k}\) の弧を辺に置き換えたとき、二つの路 \(\mathbf{p}_{i}\) と \(\mathbf{p}_{j}\) に対応する \(G\) の路が辺素でないとする (\(i \neq j\))。変換後の二つの路に共通する辺を \(e\) とする。\(e\) の端点を \(\mathbf{p}_{i}\) が通る順番で \(u\), \(v\) とする。このとき \(\mathbf{p}_{i}\) は \(e\) を (正確には、\(e\) に対応する \(G^{\operatorname*{bidir}}\) の二つの弧の一つを) \(u\) から \(v\) へ通り抜ける。
二つの路 \(\mathbf{p}_{i}\) と \(\mathbf{p}_{j}\) は弧素だから、辺 \(e\) を同じ方向に通り抜けることはない。よって \(\mathbf{p}_{j}\) は辺 \(e\) を \(v\) から \(u\) に (\(\mathbf{p}_{i}\) と逆方向に) 通り抜ける。つまり \(\mathbf{p}_{i}\) と \(\mathbf{p}_{j}\) は次の形をしている:
ここで \(e_{1}\) と \(e_{2}\) は \(e\) に対応する \(G^{\operatorname*{bidir}}\) の二つの弧を表す。この二つの路 \(\mathbf{p}_{i}\) と \(\mathbf{p}_{j}\) から次の二つの歩道を新しく構築できる13:
これらの歩道 \(\mathbf{p}_{i}^{\prime}\) と \(\mathbf{p}_{j}^{\prime}\) はどちらも \(s\) から \(t\) への歩道であり、元々 \(\mathbf{p}_{i}\) と \(\mathbf{p}_{j}\) が使っていた弧だけを含む。よって \(\mathbf{p}_{1},\mathbf{p}_{2},\ldots,\mathbf{p}_{k}\) の \(\mathbf{p}_{i}\) と \(\mathbf{p}_{j}\) 以外の任意の路と \(\mathbf{p}_{i}^{\prime}\) および \(\mathbf{p}_{j}^{\prime}\) は弧素である。さらに、\(\mathbf{p}_{i}^{\prime}\) と \(\mathbf{p}_{j}^{\prime}\) も弧素である (\(\mathbf{p}_{i}\) と \(\mathbf{p}_{j}\) が弧素であり、路である \(\mathbf{p}_{i}\) と \(\mathbf{p}_{j}\) には同じ弧が含まれないため)。また、\(\mathbf{p}_{i}^{\prime}\) と \(\mathbf{p}_{j}^{\prime}\) の長さの和は \(\mathbf{p}_{i}\) と \(\mathbf{p}_{j}\) の長さの和より \(2\) だけ小さい (\(e_{1}\) と \(e_{2}\) が使われなくなるため)。\(\mathbf{p}_{i}^{\prime}\) と \(\mathbf{p}_{j}^{\prime}\) が路とは限らないものの、(命題 4.5.8 の証明と同様に) 閉路を繰り返し除去することで路にできる。この操作を行うと、\(s\) から \(t\) への二つの路 \(\mathbf{p}_{i}^{\prime\prime}\), \(\mathbf{p}_{j}^{\prime\prime}\) が得られる。\(\mathbf{p}_{1},\mathbf{p}_{2},\ldots,\mathbf{p}_{k}\) の \(\mathbf{p}_{i}\) と \(\mathbf{p}_{j}\) 以外の任意の路と \(\mathbf{p}_{i}^{\prime\prime}\) および \(\mathbf{p}_{j}^{\prime\prime}\) は弧素であり、\(\mathbf{p}_{i}^{\prime\prime}\) と \(\mathbf{p}_{j}^{\prime\prime}\) も弧素であり、\(\mathbf{p}_{i}^{\prime\prime}\) と \(\mathbf{p}_{j}^{\prime\prime}\) の長さの和は \(\mathbf{p}_{i}\) と \(\mathbf{p}_{j}\) の長さの和より \(2\) 以上小さい。
よって、\(\{\mathbf{p}_{1},\mathbf{p}_{2},\ldots,\mathbf{p}_{k}\}\) の \(\mathbf{p}_{i}\) と \(\mathbf{p}_{j}\) を \(\mathbf{p}_{i}^{\prime\prime}\) と \(\mathbf{p}_{j}^{\prime\prime}\) に入れ替えれば、\(s\) から \(t\) への路からなる任意の二要素が弧素な \(k\) 要素集合であって全長が \(\{\mathbf{p}_{1},\mathbf{p}_{2},\ldots,\mathbf{p}_{k}\}\) より小さいものが得られる。しかしこれは、\(s\) から \(t\) への路からなる任意の二要素が弧素な \(k\) 要素集合であって全長が最小のものが \(\{\mathbf{p}_{1},\mathbf{p}_{2},\ldots,\mathbf{p}_{k}\}\) である事実と矛盾する。この矛盾は仮定が偽であることを示す。つまり路 \(\mathbf{p}_{1},\mathbf{p}_{2},\ldots,\mathbf{p}_{k}\) の弧を辺に置き換えて得られる \(k\) 個の \(G\) の路は任意の二つが辺素である。]
これで \(G\) における \(s\) から \(t\) への路からなる任意の二要素が辺素な \(k\) 要素集合 (\(\{\mathbf{p}_{1},\mathbf{p}_{2},\ldots,\mathbf{p}_{k}\}\) の弧を辺に置き換えたもの) が見つかった。よって \(k\) の定義より次の不等式を得る:
逆に、次の不等式は容易に分かる:
よって次の等式を得る:
これで Claim 1 が示せた。先述したように、以上で定理 10.1.25 は証明された。□
定理 10.1.10 と Remark 10.1.9 から定理 10.1.6 を示したのと同様の議論を使うことで、定理 10.1.25 と Remark 10.1.24 から示せる。□
\(G\) を任意の頂点の次数が偶数の多重グラフ、\(s\) と \(t\) を \(G\) の異なる二頂点とする。\(s\) から \(t\) への路からなる任意の二要素が辺素な集合の最大要素数が偶数だと示せ。
10.1.3 有向グラフの頂点に関する Menger の定理
これまでに示した Menger の定理は共通の弧 (または辺) を持たない路からなる集合を考えてきた。共通の頂点を避けたい場合には何が言えるだろうか?
\(\mathbf{p}\) をグラフまたは有向グラフの路とする。\(\mathbf{p}\) の内部頂点 (intermediate vertex) とは、\(\mathbf{p}\) の始点でも終点でもない \(\mathbf{p}\) の頂点を意味する。
あるグラフまたは有向グラフの二つの路 \(\mathbf{p}\) と \(\mathbf{q}\) が内部頂点素 (internally vertex-disjoint) とは、\(\mathbf{p}\) と \(\mathbf{q}\) が共通の内部頂点を持たないことを意味する。
例 10.1.2 の二つの路 \(\mathbf{p}\) と \(\mathbf{q}\) は弧素であるものの、内部頂点素ではない。
内部頂点素な二つの路 \(\mathbf{p}\) と \(\mathbf{q}\) の例を次に示す:
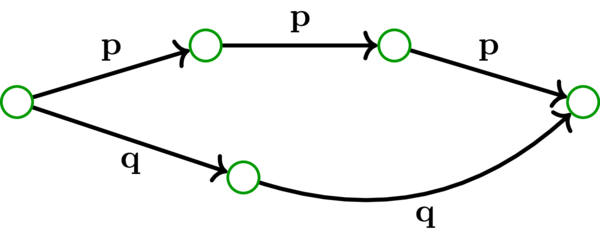
内部頂点素な路に関する自明なケースとして、長さが \(1\) 以下の路がある。つまり、長さが \(1\) 以下の路は自身を含む任意の路と内部頂点素となる (そもそも内部頂点を持たないため)。
\(D=\left( V,A,\psi\right) \) を多重有向グラフ、\(s\) と \(t\) を \(D\) の異なる二頂点とする。\(V\setminus \left\{ s,t\right\} \) の部分集合 \(W\) が \(s\)-\(t\)-内部頂点切断 (internal \(s\)-\(t\)-vertex-separator) とは、\(s\) から \(t\) への任意の路が \(W\) に属する頂点を少なくとも一つ含むことを言う。言い換えれば、\(V\setminus W\) に関する \(D\) の誘導部分有向グラフが \(s\) から \(t\) への路を持たないような \(V\setminus\left\{ s,t\right\} \) の部分集合 \(W\) を \(s\)-\(t\)-内部頂点切断と呼ぶ。
\(D=\left( V,A,\psi\right) \) を次の多重有向グラフとする:
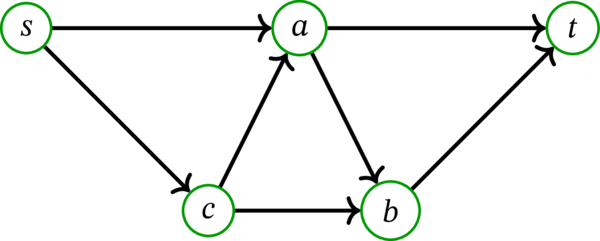
このとき、集合 \(\left\{ a,b\right\} \) と \(\left\{ a,c\right\} \) はいずれも \(s\)-\(t\)-内部頂点切断である。実際、頂点 \(a\), \(b\) または頂点 \(a\), \(c\) を除去すると \(s\) と \(t\) が切り離される。これに対して、集合 \(\left\{ a\right\} \) と \(\left\{ b,c\right\} \) はいずれも \(s\)-\(t\)-内部頂点切断でない。実際、\(c\) と \(b\) を経由する \(s\) から \(t\) への路は \(a\) を含まず、\(a\) を経由する \(s\) から \(t\) への路は \(b\) と \(c\) を含まない。
\(D=\left( V,A,\psi\right) \) を多重有向グラフ、\(s\) と \(t\) を \(D\) の異なる二頂点とする。このとき:
-
\(D\) に \(s\) から \(t\) への路が存在しないとき、かつそのときに限って空集合 \(\varnothing\) は \(s\)-\(t\)-内部頂点切断となる。
-
始点 \(s\) と終点 \(t\) を持つ弧が \(D\) に存在しないなら、集合 \(V\setminus\left\{ s,t\right\} \) は \(s\)-\(t\)-内部頂点切断である (\(s\) から \(t\) への任意の路は少なくとも一つの内部頂点を含み、その内部頂点が \(V\setminus\left\{ s,t\right\} \) に属するため)。
-
始点 \(s\) と終点 \(t\) を持つ弧が \(D\) に存在するなら、\(s\)-\(t\)-内部頂点切断は存在しない (\(s\) から \(t\) への長さ \(1\) の「直通路」が内部頂点を持たないため)。
続いて、内部頂点素な路に関する定理 10.1.6 と定理 10.1.10 を表明する:
\(D=\left( V,A,\psi\right) \) を多重有向グラフ、\(s\) と \(t\) を \(D\) の異なる二頂点とする。始点 \(s\) と終点 \(t\) を持つ弧が \(D\) に存在しないと仮定する。このとき、\(s\) から \(t\) への路からなる任意の二要素が内部頂点素な集合の最大要素数は、\(s\)-\(t\)-内部頂点切断の最小要素数に等しい。
\(D\) を次の多重有向グラフとする:
このとき、\(s\) から \(t\) への路からなる任意の二要素が内部頂点素な集合の最大要素数は \(2\) である。実際、次の図に赤と青で示された二つの路は内部頂点素である:
任意の二つが内部頂点素な \(3\) つの路は存在するだろうか? 一見しただけでは明らかでないものの、定理 10.1.32 を使うと簡単に分かる。定理 10.1.32 より、\(s\) から \(t\) への路からなる任意の二要素が内部頂点素な集合の最大要素数は \(s\)-\(t\)-内部頂点切断の最小要素数に等しい。よって、前者の値が \(2\) より大きいなら、後者の値も \(2\) より大きくなる。しかし、容易に確認できるように \(2\) 要素集合 \(\left\{ a,f\right\} \) は \(s\)-\(t\)-内部頂点切断だから、両方の値は \(2\) である。
例 10.1.11 の有向グラフ \(D\) を考える。以前の例では任意の二つが弧素な \(s\) から \(t\) への \(3\) つの路を発見した。これらの \(3\) つの路は任意の二つが内部頂点素であるわけではない (実際、茶色の路は赤色の路と青色の路のそれぞれと共通の内部頂点を持つ)。しかし、任意の二つが内部頂点素な \(s\) から \(t\) への \(3\) つの路は存在する。見つけられるだろうか?
ここでも有向グラフの弧に関する Menger の定理 (定理 10.1.10) を適切な有向グラフ \(D^{\prime}=\left( V^{\prime},A^{\prime},\psi^{\prime}\right) \) に適用する。
多重有向グラフ \(D^{\prime}\) はどんなグラフだろうか? 有向グラフ \(D\) を改変し、共通の内部頂点を持つ \(D\) の路が \(D^{\prime}\) で共通の弧を持つようにすることが基本的なアイデアとなる。最も自然な方法は次の通りである: \(D\) の各頂点 \(v\) を二つに「引きちぎる」ことで \(v^{i}\) と \(v^{o}\) という二つの頂点に置き換え、さらに始点 \(v^{i}\) と終点 \(v^{o}\) を持つ弧 \(v^{io}\) を追加する (\(v^{i}\) と \(v^{o}\) はそれぞれ「\(v\)-in」と「\(v\)-out」を表す。\(v^{i}\) は \(v\) への「入口」、\(v^{o}\) は \(v\) からの「出口」と解釈できる)。もともと \(D\) に存在する任意の弧 \(a\) は \(D^{\prime}\) で弧 \(a^{oi}\) となり、弧 \(a\) が始点 \(u\) と終点 \(v\) を持つとき弧 \(a^{oi}\) は始点 \(u^{o}\) と終点 \(v^{i}\) を持つ。
例を次に示す。\(D=\left( V,A,\psi\right) \) を次の多重有向グラフとする:
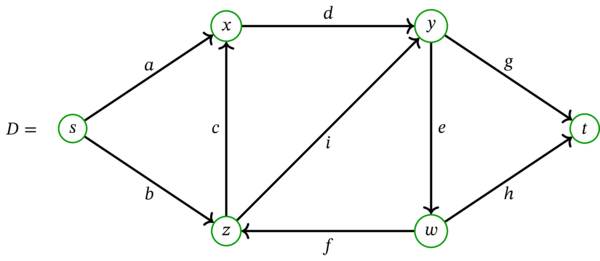
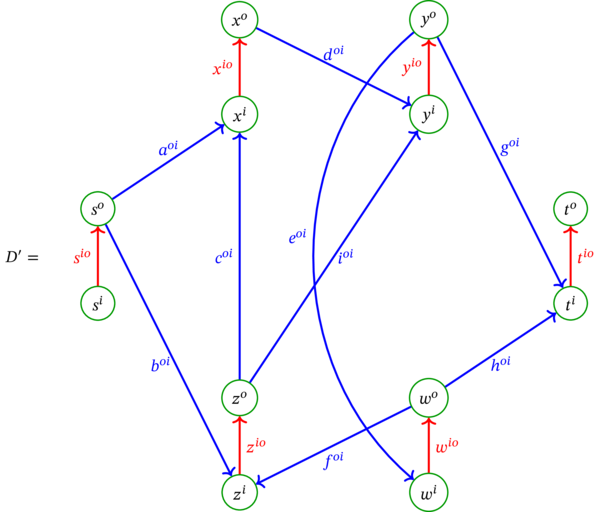
このとき \(D^{\prime}\) は次の多重有向グラフとなる:
この \(D^{\prime}\) は所望の性質を持つ: 例えば、次に示す二つの \(D\) の路は共通の頂点 \(y\) を持つ:
この二つの路に対応する \(D^{\prime}\) の路を次に示す:
この二つの路は確かに共通の弧 \(y^{io}\) を持つ。頂点が乗り換え駅、弧が駅間の接続関係を表す鉄道ネットワークが \(D\) だと考えれば、\(D^{\prime}\) は乗り換えを表す弧を持った詳細な鉄道ネットワークと考えることができる。
この多重有向グラフ \(D^{\prime}=\left( V^{\prime },A^{\prime},\psi^{\prime}\right) \) の最大限に一般化した形式的な定義を示す:
-
\(D\) の各頂点 \(v\) は \(D^{\prime}\) で二つの新しい頂点 \(v^{i}\) と \(v^{o}\) に置き換わる。\(v^{i}\) を入頂点 (in-vertex) と呼び、\(v^{o}\) を出頂点 (out-vertex) と呼ぶ。\(D^{\prime}\) の頂点集合 \(V^{\prime}\) は次のように定義される:
\[ V^{\prime}\colonequals \underbrace{\left\{ v^{i}\mid v\in V\right\} }_{\text{入頂点}}\cup\underbrace{\left\{ v^{o}\mid v\in V\right\}}_{\text{出頂点}} \] -
\(D\) の各弧 \(a \in A\) は \(D^{\prime}\) で新しい弧 \(a^{oi}\) に置き換わる。弧 \(a \in A\) が始点 \(u\) と終点 \(v\) を持つとき、\(a\) は始点 \(u^{o}\) と終点 \(v^{i}\) を持つ新しい弧 \(a^{oi}\) に置き換わる。この \(a^{oi}\) を \(D^{\prime}\) の弧弧 (arc-arc) と呼ぶ (\(D\) の弧から生まれた弧であるため)。
-
\(D\) の各頂点 \(v \in V\) ごとに、始点 \(v^{i}\) と終点 \(v^{o}\) を持つ新しい弧 \(v^{io}\) が \(D^{\prime}\) に追加される。この弧 \(v^{io}\) を \(D^{\prime}\) の頂点弧 (vertex-arc) と呼ぶ (\(D\) の頂点から生まれた弧であるため)。
-
\(D^{\prime}\) の弧集合 \(A^{\prime}\) は次のように定義される:
\[ A^{\prime}\colonequals \underbrace{\left\{ a^{oi}\mid a\in A\right\} }_{\text{弧弧}}\cup\underbrace{\left\{ v^{io}\mid v\in V\right\} }_{\text{頂点弧}} \]写像 \(\psi^{\prime}\colon A^{\prime}\rightarrow V^{\prime}\times V^{\prime}\) の定義はこれまでに説明した通りである:
-
任意の弧弧 \(a^{oi} \in A^{\prime}\) に対しては \(\psi^{\prime}\left( a^{oi}\right) \colonequals \left( u^{o},v^{i}\right) \) と定義される。ここで \(\left( u,v\right) =\psi\left( a\right) \) である。
-
任意の頂点弧 \(v^{io} \in A^{\prime}\) に対しては \(\psi^{\prime}\left( v^{io}\right) \colonequals \left( v^{i},v^{o}\right) \) と定義される。
-
\(D^{\prime}\) は「二部有向グラフ」とでも言えるグラフであることに注目してほしい: \(D^{\prime}\) の弧はどれも出頂点と入頂点を接続する。つまり、弧弧は出頂点から入頂点への弧であり、頂点弧は入頂点から出頂点への弧である。ここから、\(D^{\prime}\) の任意の歩道は弧弧と頂点弧を交互に使うことが分かる。
\(\mathbf{p}=\left( v_{0},a_{1},v_{1},a_{2},v_{2},\ldots,a_{k},v_{k}\right) \) を非自明な14 \(D\) の路とするとき、対応する \(D^{\prime}\) の路 \(\mathbf{p}^{oi}\) を次のように定義できる:
この路 \(\mathbf{p}^{oi}\) は \(\mathbf{p}\) から次の操作で構築できる:
-
始点 \(v_{0}\) を \(v_{0}^{o}\) に置き換える。
-
終点 \(v_{k}\) を \(v_{k}^{i}\) で置き換える。
-
その他の任意の頂点 \(v_{j}\) を列 \(v_{j}^{i},v_{j}^{io},v_{j}^{o}\) で置き換える。
-
任意の弧 \(a_{j}\) を \(a_{j}^{oi}\) で置き換える。
形式的でない言い方をすれば、\(\mathbf{p}\) の全ての内部頂点を二つに引きちぎった上で対応する頂点弧を間に入れると \(\mathbf{p}^{oi}\) が得られる。
\(\mathbf{p}\) が \(D\) における \(s\) から \(t\) への路なら、\(\mathbf{p}^{oi}\) は \(D^{\prime}\) における \(s^{o}\) から \(t^{i}\) への路となる。逆に、\(D^{\prime}\) における \(s^{o}\) から \(t^{i}\) への任意の路は、\(D\) における \(s\) から \(t\) への路を使って \(\mathbf{p}^{oi}\) と書ける (\(D^{\prime}\) の任意の歩道は弧弧と頂点弧を交互に使うため)。よって次の写像 \(f\) は全単射である:
さらに、\(D\) における二つの路 \(\mathbf{p}\) と \(\mathbf{q}\) が内部頂点素となるのは、\(D^{\prime}\) における二つの路 \(\mathbf{p}^{oi}\) と \(\mathbf{q}^{oi}\) が弧素となるとき、かつそのときに限る (路 \(\mathbf{p}\) の始点と終点を除く各頂点に対応する弧が \(\mathbf{p}^{oi}\) に存在するため)。
\(D^{\prime}\) における \(s^{o}\) から \(t^{i}\) への路からなる任意の二要素が弧素な集合の最大要素数を \(k\) とする。この条件を満たす \(k\) 要素集合に \(f\) の逆写像を適用すれば、\(D\) における \(s\) から \(t\) への路からなる任意の二要素が内部頂点素な \(k\) 要素集合が得られる (前段落で示した事実より)。よって次の不等式が分かる:
続いて、要素数が \(k\) 以下の \(s\)-\(t\)-内部頂点切断 \(W\subseteq V\setminus\left\{ s,t\right\} \) を見つけることが目標となる。このために、まず設定を単純化する。
\(s\) から \(t\) への路はループを含まない。また、始点 \(t\) と終点 \(s\) を持つ弧も含まない (路の頂点は相異なる必要があるため)。よって、それらを除去しても問題ない。つまり、今考えている定理 10.1.32 を証明する上では、ループおよび始点 \(t\) と終点 \(s\) を持つ弧を \(D\) から除去しても問題ない。よって有向グラフ \(D\) はそういった弧を持たないと一般性を失うことなく仮定する。定理の仮定より \(D\) は始点 \(s\) と終点 \(t\) を持つ弧を持たないので、このとき \(D\) は \(\left\{ s,t\right\} \) に属する始点と \(\left\{ s,t\right\} \) に属する終点を持つ弧を持たない (そういった弧は始点 \(t\) と終点 \(s\) を持つか、始点 \(s\) と終点 \(t\) を持つか、ループであるため)。言い換えれば、\(D\) の任意の弧は \(s\) でも \(t\) でもない端点15を少なくとも一つ持つ。
一方、\(D^{\prime}\) における \(s^{o}\) から \(t^{i}\) への路からなる任意の二要素が弧素な集合の最大要素数が \(k\) だから、定理 10.1.10 を \(D^{\prime}=\left( V^{\prime},A^{\prime},\psi^{\prime}\right) \) と \(s^{o}\), \(t^{i}\) に適用すると、\(D^{\prime}\) の \(s^{o}\)-\(t^{i}\)-カットの最小要素数も \(k\) だと分かる。つまり \(\left\vert \left[ S,\overline{S}\right] \right\vert =k\) を満たす \(D^{\prime}\) の \(s^{o}\)-\(t^{i}\)-カット \(\left[ S,\overline{S}\right] \) が存在する。\(\left[ S,\overline{S}\right] \) が \(s^{o}\)-\(t^{i}\)-カットなので、\(s^{o}\in S\) と \(t^{i}\notin S\) と \(S\subseteq V^{\prime}\) が成り立つ。
\(B\colonequals \left[ S,\overline{S}\right] \) と定める。このとき \(\left\vert B\right\vert =\left\vert \left[ S,\overline{S}\right] \right\vert =k\) である。さらに \(s^{io}\notin B\)16 と \(t^{io} \notin B\)17 も容易に分かる。
\(D^{\prime}\) の任意の頂点 \(w\in V^{\prime}\) に対して、\(D\) の頂点 \(\beta\left( w\right) \in V\) を次のように割り当てる: \(w\) は \(D^{\prime}\) の頂点より \(w=v^{i}\) または \(w=v^{o}\) を満たす頂点 \(v\) が存在するから、\(\beta\left( w\right) \colonequals v\) と定める。言い換えれば、\(\beta\left( w\right) \) は \(w\in\left\{ v^{i},v^{o}\right\} \) を満たす頂点 \(v\) である。この \(\beta\left( w\right) \) を頂点 \(w\) の基頂点 (base vertex) と呼ぶ。
任意の弧 \(b \in B\) に対して、\(b\) の少なくとも一つの端点 \(w\) は \(\beta\left( w\right) \in V\setminus\left\{ s,t\right\} \) を満たす18。この条件を満たす端点 \(w\) を任意に取り、その基頂点 \(\beta\left( w\right) \) を \(\beta\left( b\right) \) と表記する。この \(\beta\left( b\right) \) を弧 \(b\) の基頂点 (base point) と呼ぶ。定義より次が分かる:
さらに、集合 \(\left\{ \beta\left( b\right) \mid b\in B\right\} \) を \(\beta\left( B\right) \) と表記する。明らかに \(\left\vert \beta\left( B\right) \right\vert \leq\left\vert B\right\vert =k\) である。
これから次の命題を証明する:
[証明: \(D\) における \(s\) から \(t\) への路を任意に取って \(\mathbf{p}\) とする。\(\mathbf{p}\) が \(\beta\left( B\right) \) に属する頂点を含むと示せばよい。
\(D\) の路 \(\mathbf{p}\) に対して \(D^{\prime}\) の路 \(\mathbf{p}^{oi}\) を割り当てたことを思い出してほしい。\(\mathbf{p}^{oi}\) の定義より、\(\mathbf{p}^{oi}\) の任意の頂点に対応する基頂点は \(\mathbf{p}\) の頂点だと分かる (実際、\(\mathbf{p}\) の頂点が \(v_{0}\), \(v_{1}\), ..., \(v_{k}\) なら \(\mathbf{p}^{oi}\) の頂点は \(v_{0}^{o}\), \(v_{1}^{i}\), \(v_{1}^{o}\), \(v_{2}^{i}\), \(v_{2}^{o}\), ..., \(v_{k-1}^{i}\), \(v_{k-1}^{o}\), \(v_{k}^{i}\) であり、それらの基頂点は \(v_{0}\), \(v_{1}\), \(v_{1}\), \(v_{2}\), \(v_{2}\), ..., \(v_{k-1}\), \(v_{k-1}\), \(v_{k}\) である)。
\(\mathbf{p}\) は \(s\) から \(t\) への路なので、\(\mathbf{p}^{oi}\) は \(s^{o}\) から \(t^{i}\) への路である。よって \(\mathbf{p}^{oi}\) は \(S\) に属する頂点から始まって \(S\) に属さない頂点で終わる (\(s^{o} \in S\) と \(t^{i}\notin S\) より)。よって路 \(\mathbf{p}^{oi}\) はどこかで \(S\) から \(\overline{S}\) に移動する。言い換えれば、\(\mathbf{p}^{oi}\) の弧 \(b\) であって始点が \(S\) に含まれ終点が \(\overline{S}\) に含まれるものが存在する。この \(b\) は \(b\in\left[ S,\overline{S}\right] =B\) を満たすから、\(\beta\left( B\right) \) の定義より \(\beta\left( b\right) \in\beta\left( B\right) \) が成り立つ。また、\(\mathbf{p}^{oi}\) の弧である \(b\) の両端点は \(\mathbf{p}^{oi}\) の頂点である。
この弧 \(b\) の基頂点 \(\beta\left( b\right) \) に注目する。\(\beta\left( b\right) \) の定義より、\(\beta\left( b\right) \) は \(b\) の端点の基頂点である。\(b\) の両端点は \(\mathbf{p}^{oi}\) の頂点だから、\(\beta\left( b\right) \) は \(\mathbf{p}^{oi}\) の頂点の基頂点だと分かる。つまり \(\beta\left( b\right) \) は \(\mathbf{p}\) の頂点である (先述したように、\(\mathbf{p}^{oi}\) の頂点の基頂点は \(\mathbf{p}\) の頂点であるため)。言い換えれば、路 \(\mathbf{p}\) は頂点 \(\beta\left( b\right) \) を含む。\(\beta\left( b\right) \in\beta\left( B\right) \) だったから、\(\mathbf{p}\) は頂点 \(\beta\left( B\right) \) に属する頂点を含むと結論できる。以上で命題 \((2)\) は証明された。]
任意の \(b\in B\) に対して \(\beta\left( b\right) \in V\setminus\left\{ s,t\right\} \) だから、集合 \(\beta\left( B\right) \) は \(V\setminus\left\{ s,t\right\} \) の部分集合である。さらに命題 \((2)\) より、\(s\) から \(t\) への任意の路は \(\beta\left( B\right) \) に属する頂点を含む。言い換えれば、\(\beta\left( B\right) \) は \(s\) から \(t\) への任意の路が \(W\) に属する頂点を含むような部分集合 \(W\subseteq V\setminus\left\{ s,t\right\} \) である。\(s\)-\(t\)-内部頂点切断の定義より、\(\beta\left( B\right) \) は \(s\)-\(t\)-内部頂点切断だと分かる。さらに式 \((1)\) より次の不等式が分かる:
一方で、鳩ノ巣原理より19次の不等式が分かる:
二つの不等式を組み合わせれば次の等式を得る:
以上で定理 10.1.32 は証明された。□
有向グラフの弧に関する Menger の定理に多終端バージョン (定理 10.1.18) が存在したのと同じように、有向グラフの頂点に関する Menger の定理にも多終端バージョンが存在する。それを表明するには、ここでも定義がいくつか必要になる:
\(D=\left( V,A,\psi\right) \) を多重有向グラフ、\(X\) と \(Y\) を \(V\) の部分集合とする。
-
\(X\) から \(Y\) への路 (path from \(X\) to \(Y\)) とは、始点が \(X\) に属し、終点が \(Y\) に属する \(D\) の路を言う。
-
\(V\) の部分集合 \(W\) が \(X\)-\(Y\)-頂点切断 (\(X\)-\(Y\)-vertex-separator) とは、\(X\) から \(Y\) への任意の路が \(W\) に属する頂点を少なくとも一つ含むことを意味する。言い換えれば、集合 \(V \setminus W\) に関する \(D\) の誘導部分グラフが \(X\) から \(Y\) への路を持たないような \(V\) の部分集合 \(W\) を \(X\)-\(Y\)-頂点切断と呼ぶ。
-
\(X\)-\(Y\)-頂点切断 \(W\) が \(V\setminus\left( X\cup Y\right) \) の部分集合であるとき、\(W\) を\(X\)-\(Y\)-内部頂点切断 (internal \(X\)-\(Y\)-vertex-separator) と呼ぶ。
\(D=\left( V,A,\psi\right) \) を多重有向グラフ、共通要素を持たない二つの \(V\) の部分集合を \(X\), \(Y\) とする。\(X\) に属する始点と \(Y\) に属する終点を持つ弧が \(D\) に存在しないと仮定する。
このとき、\(X\) から \(Y\) への路からなる任意の二要素が内部頂点素な集合の最大要素数は、\(X\)-\(Y\)-内部頂点切断の最小要素数に等しい。
多重有向グラフ \(D\) および \(D\) の頂点集合の部分集合 \(X\), \(Y\) を次のように定める:
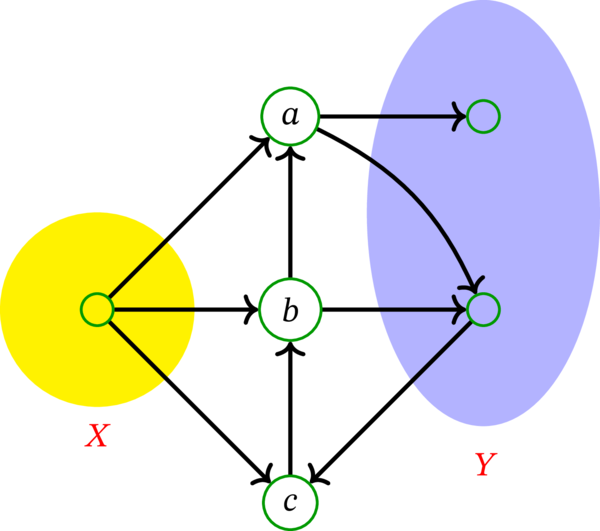
このとき、\(X\) から \(Y\) への路からなる任意の二要素が内部頂点素な集合の最大要素数は \(2\) である。実際、次の図に赤と青で示す内部頂点素な二つの路が存在する:
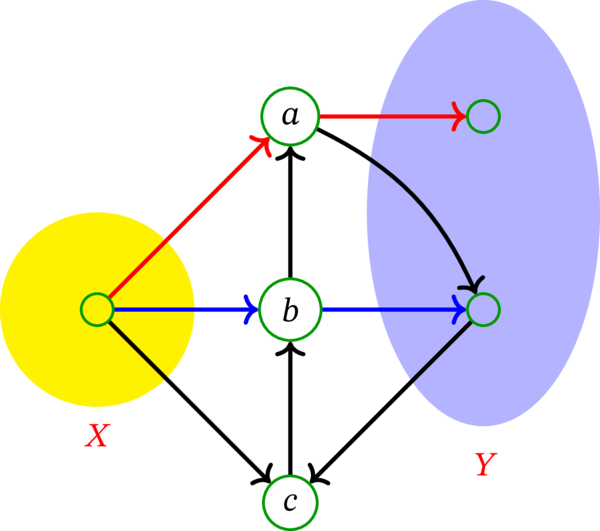
\(X\)-\(Y\)-内部頂点切断の最小要素数も \(2\) である。実際、\(2\) 要素の \(X\)-\(Y\)-内部頂点切断として集合 \(\left\{ a,b\right\} \) がある。定理 10.1.36 が主張するように、二つの値は確かに等しい。
定理 10.1.18 と同様の方法で新しい多重有向グラフ \(D^{\prime}=\left( V^{\prime},A^{\prime},\psi^{\prime}\right) \) を構築する。\(X\) に属する始点と \(Y\) に属する終点を持つ弧が \(D\) に存在しないので、\(D^{\prime}\) には始点 \(s\) と終点 \(t\) を持つ弧が存在しない。
よって定理 10.1.32 を \(D^{\prime}=\left( V^{\prime },A^{\prime},\psi^{\prime}\right) \) に適用すれば、\(D^{\prime}\) における \(s\) から \(t\) への路からなる任意の二要素が内部頂点素な集合の最大要素数が \(D^{\prime}\) の \(s\)-\(t\)-内部頂点切断の最小要素数に等しいと分かる。
この結果が元の \(D\) に関して何を示すかを考えよう:
-
\(D^{\prime}\) の \(s\)-\(t\)-内部頂点切断の最小要素数は、\(D\) の \(X\)-\(Y\)-内部頂点切断の最小要素数に等しい (実際、\(D^{\prime}\) の \(s\)-\(t\)-内部頂点切断は全て \(D\) の \(X\)-\(Y\)-内部頂点切断でもある20)。
-
\(D^{\prime}\) における \(s\) から \(t\) への路からなる任意の二要素が内部頂点素な集合の最大要素数は、\(D\) における \(X\) から \(Y\) への路からなる任意の二要素が内部頂点素な集合の最大要素数に等しい21。
よって前段落の結果は定理 10.1.36 に等しく、これで証明は完了した。□
この定理には (内部頂点素ではなく) 頂点素な路という概念を利用する別バージョンがある。こちらの方が定義は単純になる:
あるグラフまたは有向グラフの二つの路 \(\mathbf{p}\) と \(\mathbf{q}\) が共通の頂点を持たないとき、\(\mathbf{p}\) と \(\mathbf{q}\) は頂点素 (vertex-disjoint) と言う。
\(D=\left( V,A,\psi\right) \) を多重有向グラフ、共通要素を持たない二つの \(V\) の部分集合を \(X\), \(Y\) とする。
このとき、\(X\) から \(Y\) への路からなる任意の二要素が頂点素な集合の最大要素数は \(X\)-\(Y\)-頂点切断の最小要素数に等しい。
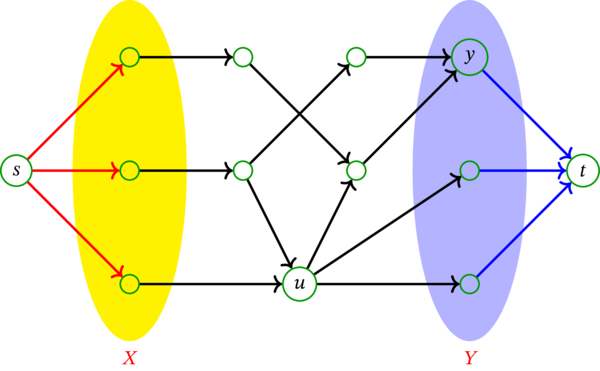
有向グラフ \(D\) および \(D\) の頂点集合の部分集合 \(X\), \(Y\) を次のように定める:
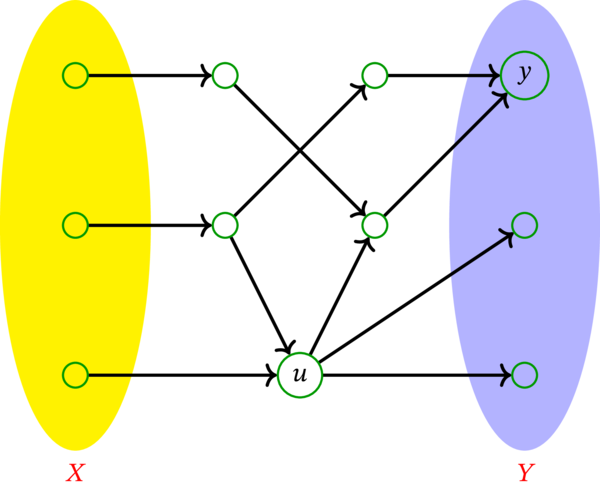
このとき、\(X\) から \(Y\) への路からなる任意の二要素が頂点素な集合の最大要素数は \(2\) である。実際、次の図に赤と青で示す頂点素な二つの路が存在する:
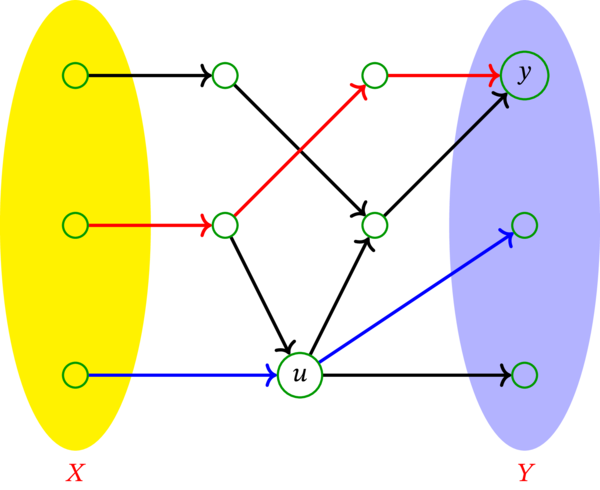
もし任意の二要素が内部頂点素な路の集合を考えているなら、さらにもう一つ路 (具体的には、\(X\) の一番上の頂点から始まって \(Y\) の一番上の頂点で終わる路) を取ることができる。しかし、この路と赤い路は内部頂点素ではあるものの頂点素ではない。少し考えれば、\(X\) から \(Y\) への路からなる任意の二要素が頂点素な集合の最大要素数が \(2\) であることが分かる。
\(X\)-\(Y\)-頂点切断の最小要素数も \(2\) である。実際、要素数 \(2\) の \(X\)-\(Y\)-頂点切断として \(\left\{ u,y\right\} \) がある。定理 10.1.39 が主張するように、この値は \(X\) から \(Y\) への路からなる任意の二要素が頂点素な集合の最大要素数に等しい。
示すべき命題を定理 10.1.32 に帰着させる。ここでも有向グラフを適切に変更するアプローチを用いるが、施す変更は非常に単純である: 二つの新しい頂点 \(s\), \(t\) を \(D\) に追加し、\(s\) から全ての \(x\in X\) への弧および全ての \(y\in Y\) から \(t\) への弧を追加する (全部で \(\left\vert X\right\vert +\left\vert Y\right\vert \) 本の新しい弧が追加される)。こうして得られる多重有向グラフを \(D^{\prime}\) とする。詳しく言えば、\(D^{\prime}\) の定義は次の通りである:
-
新しい頂点 \(s\) と \(t\) を作成し、\(V^{\prime}\colonequals V\cup\left\{ s,t\right\} \) と定める。この集合 \(V^{\prime}\) は \(D^{\prime}\) の頂点集合となる。
-
頂点 \(x\in X\) ごとに新しい弧 \(a_{x}\) を作成する。弧 \(a_{x}\) は始点 \(s\) と終点 \(x\) を持つ。
-
頂点 \(y \in Y\) ごとに新しい弧 \(b_{y}\) を作成する。弧 \(b_{y}\) は始点 \(y\) と終点 \(t\) を持つ。
-
\(a_{x}\) と \(b_{y}\) を使って \(A^{\prime}\colonequals A\cup\left\{ a_{x}\mid x\in X\right\} \cup\left\{ b_{y}\mid y\in Y\right\} \) と定める。この集合 \(A^{\prime}\) は \(D^{\prime}\) の弧集合となる。
-
写像 \(\psi\colon A\rightarrow V\times V\) を次のように拡張して写像 \(\psi^{\prime }\colon A^{\prime}\rightarrow V^{\prime}\times V^{\prime}\) を定める:
\[ \begin{alignedat}{3} & \psi^{\prime}\left( a_{x}\right) && = \left( s,x\right) \quad & (\forall x \in X) \\ & \psi^{\prime}\left( b_{y}\right) && = \left( y,t\right) \quad & (\forall y \in Y) \\ & \psi^{\prime}\left( c\right) && =\psi\left( c\right) \quad & (\forall c \in A) \end{alignedat} \] -
多重有向グラフ \(\left( V^{\prime },A^{\prime},\psi^{\prime}\right) \) を \(D^{\prime}\) と定める。
例えば、\(D\) が例 10.1.40 の多重有向グラフなら、\(D^{\prime}\) は次の多重有向グラフとなる:
弧 \(a_{x}\) は赤で、弧 \(b_{y}\) は青で描かれている。
\(D^{\prime}\) の構成より、\(D^{\prime}\) は始点 \(s\) と終点 \(t\) を持つ弧を持たない。よって \(D^{\prime }=\left( V^{\prime},A^{\prime},\psi^{\prime}\right) \) には定理 10.1.32 を適用できる。よって \(s\) から \(t\) への路からなる任意の二頂点が内部頂点素な集合の最大要素数は \(s\)-\(t\)-内部頂点切断の最小要素数に等しい。一方で、次の二つの命題は容易に分かる:
命題 2: \(D^{\prime}\) の \(s\)-\(t\)-内部頂点切断の最小要素数は、\(D\) の \(X\)-\(Y\)-頂点切断の最小要素数に等しい。
[命題 1 の証明の概要: \(D^{\prime}\) における \(s\) から \(t\) への任意の路を \(\mathbf{p}\) とする。\(\mathbf{p}\) の始点と終点を除去すると、\(D\) における \(X\) から \(Y\) への路が得られる。この路を \(\overline{\mathbf{p}}\) とする。この操作は次の写像を定める:
容易に分かるように、この写像は全単射である (実際、\(X\) から \(Y\) への路 \(\mathbf{q}\) が与えらたとき、先頭に \(s\) と適切な \(a_{x}\) を、末尾に適切な \(b_{y}\) と \(t\) を \(\mathbf{q}\) に追加することで \(s\) から \(t\) への路 \(\mathbf{p}\) を構築でき、この \(\mathbf{p}\) は \(\overline{\mathbf{p}} = \mathbf{q}\) を満たす)。さらに、\(s\) から \(t\) への二つの路 \(\mathbf{p}\) と \(\mathbf{q}\) が内部頂点素となるのは、対応する路 \(\overline{\mathbf{p}}\) と \(\overline{\mathbf{q}}\) が頂点素なとき、かつそのときに限る (\(\mathbf{p}\) の内部頂点は \(\overline{\mathbf{p}}\) の頂点であり、\(\mathbf{q}\) の内部頂点は \(\overline{\mathbf{q}}\) の頂点であるため)。ここから命題 1 が証明される。]
[命題 2 の証明の概要: \(D^{\prime}\) の \(s\)-\(t\)-内部頂点切断と \(D\) の \(X\)-\(Y\)-頂点切断が等しいことは容易に分かる (これを示すには、命題 1 で言及した全単射と \(V^{\prime}\setminus\left\{ s,t\right\} =V\) を使って二つの概念の定義を比較する)。ここから命題 2 が証明される。]
\(s\) から \(t\) への路からなる任意の二頂点が内部頂点素な集合の最大要素数は \(s\)-\(t\)-内部頂点切断の最小要素数に等しいので、命題 1 と命題 2 より次が分かる: \(X\) から \(Y\) への路からなる任意の二要素が頂点素な集合の最大要素数は \(X\)-\(Y\)-頂点切断の最小要素数に等しい。以上で定理 10.1.39 は証明された。□
なお、Hall の結婚定理 (定理 8.3.4) は有向グラフに関する Menger の定理のどれを使っても容易に証明できる [練習問題!]。逆方向の証明も可能だと聞いたことがある。このため、Menger の定理は Hall の結婚定理と同値な定理群 (König の定理など) に含まれると言える。
10.1.4 無向グラフの頂点に関する Menger の定理
無向グラフの頂点に関する Menger の定理も存在する。定理 10.1.32、定理 10.1.36、定理 10.1.39 に対応する定理を必要な定義と共に示す:
\(G=\left( V,E,\varphi\right) \) を多重グラフ、\(s\) と \(t\) を \(G\) の異なる二頂点とする。\(V\setminus \left\{ s,t\right\} \) の部分集合 \(W\) が \(s\)-\(t\)-内部頂点切断 (internal \(s\)-\(t\)-vertex-separator) とは、\(s\) から \(t\) への任意の路が \(W\) に属する頂点を少なくとも一つ含むことを言う。言い換えれば、\(V\setminus W\) に関する \(G\) の誘導部分グラフが \(s\) から \(t\) への路を持たないような \(V\setminus\left\{ s,t\right\} \) の部分集合 \(W\) を \(s\)-\(t\)-内部頂点切断と呼ぶ。
\(G=\left( V,E,\varphi\right) \) を多重グラフ、\(s\) と \(t\) を \(G\) の異なる二頂点とする。\(s\) と \(t\) を端点とする辺が \(G\) に存在しないと仮定する。このとき、\(s\) から \(t\) への路からなる任意の二要素が内部頂点素な集合の最大要素数は、\(s\)-\(t\)-内部頂点切断の最小要素数に等しい。
\(G=\left( V,E,\varphi\right) \) を多重グラフ、\(X\), \(Y\) を \(V\) の部分集合とする。
-
\(X\) から \(Y\) への路 (path from \(X\) to \(Y\)) とは、始点が \(X\) に属し、終点が \(Y\) に属する \(D\) の路を言う。
-
\(V\) の部分集合 \(W\) が \(X\)-\(Y\)-頂点切断 (\(X\)-\(Y\)-vertex-separator) とは、\(X\) から \(Y\) への任意の路が \(W\) に属する頂点を少なくとも一つ含むことを意味する。言い換えれば、集合 \(V \setminus W\) に関する \(G\) の誘導部分グラフが \(X\) から \(Y\) への路を持たないような \(V\) の部分集合 \(W\) を \(X\)-\(Y\)-頂点切断と呼ぶ。
-
\(X\)-\(Y\)-頂点切断 \(W\) が \(V\setminus\left( X\cup Y\right) \) の部分集合であるとき、\(W\) を\(X\)-\(Y\)-内部頂点切断 (internal \(X\)-\(Y\)-vertex-separator) と呼ぶ。
\(G=\left( V,E,\varphi\right) \) を多重グラフ、共通要素を持たない二つの \(V\) の部分集合を \(X\) と \(Y\) とする。\(X\) に属する頂点と \(Y\) に属する頂点を端点に持つ辺が \(G\) に存在しないと仮定する。
このとき、\(X\) から \(Y\) への路からなる任意の二要素が内部頂点素な集合の最大要素数は、\(X\)-\(Y\)-内部頂点切断の最小要素数に等しい。
\(G=\left( V,E,\varphi\right) \) を多重グラフ、共通要素を持たない二つの \(V\) の部分集合を \(X\) と \(Y\) とする。
このとき、\(X\) から \(Y\) への路からなる任意の二要素が頂点素な集合の最大要素数は、\(X\)-\(Y\)-頂点切断の最小要素数に等しい。
定理 10.1.42、定理 10.1.44、定理 10.1.45 は有向グラフに対する同様の命題 (つまり定理 10.1.32、定理 10.1.36、定理 10.1.39) を \(G^{\operatorname*{bidir}}\) に適用すれば直ちに得られる (\(G\) の路と \(G^{\operatorname*{bidir}}\) の路の間に全単射が存在するため)。
-
未定義の用語は以降で定義される。 ↩︎
-
証明: 任意の弧 \(a \in A\) が \(f_{\mathbf{p}}\left( a\right) \leq f\left( a\right) \) を満たすと示せばよい。
\(a \in A\) を任意の弧とする。\(a\) が \(\mathbf{p}\) の弧でないなら、\(f_{\mathbf{p}}\) の定義から \(f_{\mathbf{p}}\left( a\right) =0\leq f\left( a\right) \) が分かる (後半の不等式は \(f\) がフローである事実から分かる)。続いて \(a\) が \(\mathbf{p}\) の弧である場合を考える。\(\mathbf{p}\) は \(D^{\prime}\) の路なので、このとき \(a\) は \(D^{\prime}\) の弧となる。\(A^{\prime}\) の定義より、これは \(f\left( a\right) >0\) を意味する。\(f\left( a\right) \) は整数だから、\(f\left( a\right) \geq1=f_{\mathbf{p}}\left( a\right) \) を得る。言い換えれば \(f_{\mathbf{p}}\left( a\right) \leq f\left( a\right) \) である。以上で示したい命題は証明された。 ↩︎
-
二つのフロー \(g\), \(h\) が \(h \leq g\) を満たすなら \(g -h\) もフローになるという (簡単に証明できる) 事実を使っている。 ↩︎
-
二つのフロー \(g\), \(h\) が \(h\leq g\) を満たすとき \(\left\vert g-h\right\vert =\left\vert g\right\vert -\left\vert h\right\vert \) が成り立つという (簡単に証明できる) 事実を使っている。\(g = f\) および \(h=f_{\mathbf{p}}\) とすれば \(\left\vert f-f_{\mathbf{p}}\right\vert =\underbrace{\left\vert f\right\vert }_{=m}-\underbrace{\left\vert f_{\mathbf{p}}\right\vert }_{=1}=m-1\) を得る。 ↩︎
-
証明: 背理法で示す。\(m\) 個の路の中に、弧素でない二つの路が存在すると仮定する。このとき、二つの弧 \(\mathbf{p}_{i}\), \(\mathbf{p}_{j}\) (\(i \neq j\)) の両方に含まれる \(a\) が存在する。この弧 \(a\) と添え字 \(i\), \(j\) に注目する。\(\mathbf{p}_{i}\) が \(a\) を含むので \(f_{\mathbf{p}_{i}}\left( a\right) =1\) が分かり、同様に \(f_{\mathbf{p}_{j}}\left( a\right) =1\) も分かる。一方 \(f_{\mathbf{p}_{1}}+f_{\mathbf{p}_{2}}+\cdots+f_{\mathbf{p}_{m}}\leq f\) からは次の不等式を得る:
\[ \begin{aligned} \left( f_{\mathbf{p}_{1}}+f_{\mathbf{p}_{2}}+\cdots+f_{\mathbf{p}_{m}}\right) \left( a\right) & \leq f\left( a\right) \\ & \leq c\left( a\right) && \left(\because\ \text{フローの容量制約}\right) \\ & =1 && \left(\because\ \text{全ての弧は容量が }1\right) \end{aligned} \]よって次が分かる:
\[ \begin{aligned} 1 & \geq\left( f_{\mathbf{p}_{1}}+f_{\mathbf{p}_{2}}+\cdots+f_{\mathbf{p}_{m}}\right) \left( a\right) \\ & = f_{\mathbf{p}_{1}}\left( a\right) +f_{\mathbf{p}_{2}}\left( a\right) +\cdots+f_{\mathbf{p}_{m}}\left( a\right) \\ & \geq\underbrace{f_{\mathbf{p}_{i}}\left( a\right) }_{=1}+\underbrace{f_{\mathbf{p}_{j}}\left( a\right) }_{=1}\ \ \ \ \ \ \ \ \ \ \left(\begin{array}{c}\because\ i \neq j \text{ より } f_{\mathbf{p}_i} \text{ と } f_{\mathbf{p}_j} \text{ は和における異なる項であり、}\\ \text{任意の } \mathbf{p} \text{ に対して } f_{\mathbf{p}} (a) \geq 0 \text{ が成り立つ} \end{array} \right) \\ & =1+1>1 \end{aligned} \]これは矛盾なので、仮定は偽だと分かる。つまり考えていた \(m\) 個の路の任意の二つは弧素である。 ↩︎
-
証明: \(f_{\mathbf{p}_{1}}\), \(f_{\mathbf{p}_{2}}\), ..., \(f_{\mathbf{p}_{m}}\) はそれぞれ路フローでありフローの保存制約を満たすので、その和 \(f_{\mathbf{p}_{1}}+f_{\mathbf{p}_{2}}+\cdots +f_{\mathbf{p}_{m}}\) も保存制約を満たす。この和がフローの容量制約を満たすことをまず確認する。
弧 \(a \in A\) を任意に取って固定する。\(m\) 個の路 \(\mathbf{p}_{1}\), \(\mathbf{p}_{2}\), ..., \(\mathbf{p}_{m}\) は任意の二つが弧素なので、 \(a\) を含む路は \(\mathbf{p}_{1}\), \(\mathbf{p}_{2}\), ..., \(\mathbf{p}_{m}\) の中に最大でも一つしか存在しない。言い換えれば、値 \(f_{\mathbf{p}_{1}}\left( a\right)\), \(f_{\mathbf{p}_{2}}\left( a\right)\), ..., \(f_{\mathbf{p}_{m}}\left( a\right) \) は最大でも一つが \(1\) であり、他は全て \(0\) である。つまり和 \(f_{\mathbf{p}_{1}}\left( a\right) +f_{\mathbf{p}_{2}}\left( a\right) +\cdots+f_{\mathbf{p}_{m}}\left( a\right) \) は \(0\) か \(1\) であり、\(f_{\mathbf{p}_{1}}\left( a\right) +f_{\mathbf{p}_{2}}\left( a\right) +\cdots+f_{\mathbf{p}_{m}}\left( a\right) \in\left\{ 0,1\right\} \) が分かる。よって次を得る:
\[ \left( f_{\mathbf{p}_{1}}+f_{\mathbf{p}_{2}}+\cdots+f_{\mathbf{p}_{m}}\right) \left( a\right) =f_{\mathbf{p}_{1}}\left( a\right)+f_{\mathbf{p}_{2}}\left( a\right) +\cdots+f_{\mathbf{p}_{m}}\left(a\right) \in\left\{ 0,1\right\} \]任意の弧の容量は \(1\) だから、次の不等式を得る:
\[ 0\leq\left( f_{\mathbf{p}_{1}}+f_{\mathbf{p}_{2}}+\cdots+f_{\mathbf{p}_{m}}\right) \left( a\right) \leq1=c\left( a\right) \]\(a\) は任意の弧だったから、写像 \( f_{\mathbf{p}_{1}}+f_{\mathbf{p}_{2}}+\cdots+f_{\mathbf{p}_{m}}\) がフローの容量制約を満たすことがこれで証明できた。よって、この写像はフローである (フローの保存制約を満たすことは先述した)。
後は、このフローの値が \(m\) であることを示せばよい。これは易しい: フローの値の定義から容易に分かるように、任意のフロー \(g_{1},g_{2},\ldots,g_{k}\) に対して \(\left\vert g_{1}+g_{2}+\cdots+g_{k}\right\vert =\left\vert g_{1}\right\vert +\left\vert g_{2}\right\vert +\cdots+\left\vert g_{k}\right\vert \) が成り立つ。よって次の等式が成り立つ:
\[ \left\vert f_{\mathbf{p}_{1}}+f_{\mathbf{p}_{2}}+\cdots+f_{\mathbf{p}_{m}}\right\vert =\left\vert f_{\mathbf{p}_{1}}\right\vert +\left\vert f_{\mathbf{p}_{2}}\right\vert +\cdots+\left\vert f_{\mathbf{p}_{m}}\right\vert =\sum_{k=1}^{m}\underbrace{\left\vert f_{\mathbf{p}_{k}}\right\vert }_{=1}=\sum_{k=1}^{m}1=m \]つまり、フロー \( f_{\mathbf{p}_{1}}+f_{\mathbf{p}_{2}}+\cdots+f_{\mathbf{p}_{m}}\) の値は \(m\) である。 ↩︎
-
「\(x\)」「\(n_{c}\)」「\(n_{s}\)」という記号の並びを不思議に思ったかもしれない。ここで \(x\) は「maximum (最大)」、\(n\) は 「minimum (最小)」を意味する。添え字の \(c\) と \(s\) の意味は明らかだろう。 ↩︎
-
証明: \(x\) の定義より、\(s\) から \(t\) への路からなる任意の二要素が弧素な集合で要素数が \(x\) のものが存在する。この集合に含まれる \(x\) 個の路を \(\mathbf{p}_{1}\), \(\mathbf{p}_{2}\), ..., \(\mathbf{p}_{x}\) とする。\(n_{s}\) の定義より、要素数が \(n_{s}\) の \(s\)-\(t\)-弧切断が存在する。この \(s\)-\(t\)-弧切断を \(B\) とする。
\(s\)-\(t\)-弧切断の定義より、\(s\) から \(t\) への任意の路は \(B\) に属する弧を少なくとも一つ含む。よって特に、\(x\) 個の路 \(\mathbf{p}_{1}\), \(\mathbf{p}_{2}\), ..., \(\mathbf{p}_{x}\) はどれも \(B\) に属する弧を少なくとも一つ含む。これら \(x\) 個の弧は相異なる (\(\mathbf{p}_{1}\), \(\mathbf{p}_{2}\), ..., \(\mathbf{p}_{m}\) の任意の二つは弧素であるため)。よって少なくとも \(x\) 個の弧は \(B\) に属する。つまり \(\left\vert B\right\vert \geq x\) である。一方 \(B\) の要素数が \(n_{s}\) だったから \(\left\vert B\right\vert =n_{s}\) であり、\(n_{s}=\left\vert B\right\vert \geq x\) つまり \(x\leq n_{s}\) を得る。 ↩︎
-
詳しく言えば:
-
\(D^{\prime}\) の任意の \(s\)-\(t\)-カットは \(s \in S\) と \(t \notin S\) を満たす \(V\) の部分集合 \(S\) を使って \(\left[ S,\overline {S}\right] \) と書ける。この \(s\)-\(t\)-カットは \(S^{\prime}\colonequals \left( S\setminus\left\{ s\right\} \right) \cup X\) と定義される \(V\) の部分集合 \(S^{\prime}\) を使って \(\left[ S^{\prime},\, \overline{S^{\prime}}\right] \) とも書けるので、\(D\) の \(X\)-\(Y\)-カットでもある。
-
逆に、\(D\) 任意の \(X\)-\(Y\)-カットは \(X\subseteq S\) と \(Y\subseteq\overline{S}\) を満たす \(V\) の部分集合 \(S\) を使って \(\left[ S,\overline {S}\right] \) と書ける。この \(X\)-\(Y\)-カットは \(S^{\prime}\colonequals \left( S\setminus X\right) \cup\left\{ s\right\} \) と定義される \(V\) の部分集合 \(S^{\prime}\) を使って \(\left[ S^{\prime},\, \overline{S^{\prime}}\right] \) とも書けるので、\(D^{\prime}\) の \(s\)-\(t\)-カットでもある。
-
-
\(G^{\operatorname*{bidir}}\) は \(G\) の全ての (無向) 辺を同じ端点を接続する逆方向の二つの有向辺に置き換えて得られる多重有向グラフを意味する。つまり、\(u\) と \(v\) を端点に持つ \(G\) の辺は、\(G^{\operatorname*{bidir}}\) において始点 \(u\) および終点 \(v\) を持つ弧と始点 \(v\) および終点 \(u\) を持つ弧に置き換わる。形式的な定義は定義 4.4.2 で与えた。 ↩︎
-
「有向 \(s\)-\(t\)-カット」は単に有向グラフにおける \(s\)-\(t\)-カットを意味する。 ↩︎
-
証明: \(s \in S\) と \(t \notin S\) を満たす任意の \(V\) の部分集合 \(S\) に対して、\(G^{\operatorname*{bidir}}\) の有向 \(s\)-\(t\)-カット \(\left[ S,\overline{S}\right] \) と \(G\) の無向 \(s\)-\(t\)-カット \(\left[ S,\overline{S}\right] _{\operatorname*{und}}\) の要素数は等しい。なぜなら、\(\left[ S,\overline{S}\right] _{\operatorname*{und}}\) に属する任意の辺は \(\left[ S,\overline{S}\right] \) に属するちょうど一つの辺に対応するからである。よって \(G^{\operatorname*{bidir}}\) の有向 \(s\)-\(t\)-カットの要素数からなる集合は \(G\) の無向 \(s\)-\(t\)-カットの要素数からなる集合と等しい。特に、両者の最小値は等しい。以上で Claim 2 は証明された。 ↩︎
-
\(\mathbf{p}_{i}\) (赤) と \(\mathbf{p}_{i}\) (青) の例を次に示す:
対応する \(\mathbf{p}^{\prime}_{i}\) (赤) と \(\mathbf{p}^{\prime}_{i}\) (青) を次に示す:
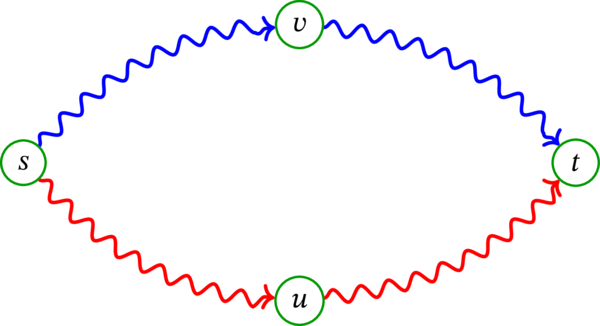
両方の図において、波線は複数の弧からなる部分を表す。 ↩︎
-
路が非自明 (nontrivial) とは、長さが \(1\) 以上であることを言う。 ↩︎
-
弧の端点 (endpoint) とは、弧の始点または終点である頂点を言う。 ↩︎
-
証明: もし \(s^{io}\in\left[ S,\overline{S}\right] \) なら \(s^{i}\in S\) と \(s^{o}\in\overline{S}\) が成り立つ。しかし \(s^{o}\in\overline{S}\) は \(s^{o} \in S\) と矛盾するので、\(s^{io}\in\left[ S,\overline{S}\right] \) ではない。言い換えれば \(s^{io}\in \left[ S,\overline {S}\right] = B\) は偽であり、\(s^{io}\notin B\) が成り立つ。 ↩︎
-
証明: もし \(t^{io}\in\left[ S,\overline {S}\right] \) なら \(t^{i}\in S\) と \(t^{o}\in\overline{S}\) が成り立つ。しかし \(t^{i}\in S\) は \(t^{i}\in\overline{S}\) と矛盾するので、\(t^{io}\in\left[ S,\overline{S}\right] \) ではない。言い換えれば \(t^{io}\in \left[ S,\overline {S}\right] = B\) は偽であり、\(t^{io}\notin B\) が成り立つ。 ↩︎
-
証明: 弧 \(b \in B\) を任意に取る。\(\beta\left( w\right) \in V\setminus\left\{ s,t\right\} \) を満たす \(b\) の端点 \(w\) が少なくとも一つ存在すると示せばよい。
\(b\) は \(D^{\prime}\) の弧だから、頂点弧または弧弧のいずれかである。よって次の二つの場合を考えればよい:
-
Case 1: 弧 \(b\) は頂点弧である。
-
Case 2: 弧 \(b\) は弧弧である。
Case 1 を最初に考える。\(b\) が頂点弧だから、ある \(v \in V\) で \(b = v^{io}\) となる。この \(v\) に注目する。\(v^{io} = b \in B\) より \(v \neq s\) が分かる (\(v=s\) なら \(v^{io}=s^{io}\notin B\) だが、これは \(v^{io}\in B\) と矛盾する)。また、\(v\neq t\) も分かる (\(v = t\) なら \(v^{io}=t^{io}\notin B\) だが、これは \(v^{io}\in B\) と矛盾する)。よって \(v\in V\setminus\left\{ s,t\right\} \) を得る。よって \(v^{i}\) は \(b\) の端点であり \(\beta\left( v^{i}\right) =v\in V\setminus\left\{ s,t\right\} \) を満たす。これで Case 1 の証明は完了した。
Case 2 を次に考える。\(b\) が弧弧だから、ある \(a \in A\) で \(b=a^{oi}\) となる。この \(a\) に注目する。\(a \in A\) より \(a\) は \(D\) の弧なので、少なくとも一つの端点は \(s\) でも \(t\) でもない (先述したように、\(D\) の各弧は \(s\) でも \(t\) でもない端点を少なくとも一つ持つ)。そのような端点を任意に取って \(x\) とする。このとき \(x \in V \setminus \{s,t\}\) が成り立つ。
一方 \(x\) は \(a\) の端点である。言い換えれば、\(x\) は \(a\) の始点または終点である。よって \(D^{\prime}\) の弧 \(a^{oi}\) は始点 \(x^{o}\) または終点 \(x^{i}\) を持つ (\(a^{oi}\) の定義より)。つまり、\(D^{\prime}\) の弧 \(b = a^{oi}\) は始点 \(x^{o}\) または終点 \(x^{i}\) を持つ。\(\beta\left( x^{o}\right) =x\in V\setminus\left\{ s,t\right\} \) と \(\beta\left( x^{i}\right) =x\in V\setminus\left\{ s,t\right\} \) が成り立つから、\(D^{\prime}\) の弧 \(b\) は \(\beta\left( w\right) \in V\setminus\left\{ s,t\right\} \) を満たす端点 \(w\) を持つ (\(b\) が始点 \(x^{o}\) を持つときは \(w = x^{o}\) であり、終点 \(x^{i}\) を持つときは \(w = x^{i}\) である)。以上で Case 2 の証明は完了した。
二つの場合で証明が完了したので、示したい命題は証明された。 ↩︎
-
-
より詳しい証明: \(s\)-\(t\)-内部頂点切断の最小要素数を \(n\) とする。\(D\) における \(s\) から \(t\) への路からなる任意の二要素が内部頂点素な集合の最大要素数を \(x\) とする。\(n \geq x\) を示せばよい。
背理法で示す。\(n < x\) と仮定する。\(n\) の定義より、要素数が \(n\) の \(s\)-\(t\)-内部頂点切断 \(W\) が存在する。\(W\) は \(s\)-\(t\)-内部頂点切断だから \(V\setminus\left\{ s,t\right\} \) の部分集合であり、\(s\) から \(t\) への任意の路は \(W\) に属する頂点を含む。さらに、\(W\) は \(n\) 要素集合より \(\left\vert W\right\vert =n < x\) を得る。
\(x\) の定義より、\(D\) における \(s\) から \(t\) への路からなる任意の二要素が内部頂点素な \(x\) 要素集合が存在する。この集合を \(\{\mathbf{p}_{1},\mathbf{p}_{2},\ldots,\mathbf{p}_{x}\}\) とする。これら \(x\) 個の路のそれぞれは \(W\) に属する頂点を少なくとも一つ含む (\(W\) が \(s\)-\(t\)-内部頂点切断であるため)。\(\left\vert W\right\vert < x\) と鳩の巣原理より、\(x\) 個の路の中に \(W\) に属する同じ頂点を含む路の組が存在することが分かる。言い換えれば、ある頂点 \(w \in W\) を含む二つの路 \(\mathbf{p}_{i}\), \(\mathbf{p}_{j}\) (\(i \neq j\)) が存在する。\(w \in W \subseteq V \setminus \{s,t\}\) だから、\(w\) は路 \(\mathbf{p}_{i}\) の始点 \(s\) でも終点 \(t\) でもない。つまり \(w\) は \(\mathbf{p}_{i}\) の内部頂点である。同様に \(w\) は \(\mathbf{p}_{j}\) の内部頂点でもある。
一方、\(\mathbf{p}_{i}\) と \(\mathbf{p}_{j}\) は内部頂点素だから、共通の内部頂点を持たない。これは \(w\) が \(\mathbf{p}_{i}\) と \(\mathbf{p}_{j}\) に共通する内部頂点である事実と矛盾する。この矛盾から仮定が偽だと分かる。つまり \(n \geq x\) が証明された。 ↩︎
-
証明: \(D^{\prime }\) の \(s\)-\(t\)-内部頂点切断、および \(D\) の \(X\)-\(Y\)-内部頂点切断の定義を思い出せば、次が分かる:
-
\(D^{\prime}\) の \(s\)-\(t\)-内部頂点切断とは、\(s\) から \(t\) への任意の路が \(W\) に属する頂点を少なくとも一つ含むような \(V^{\prime}\setminus\left\{ s,t\right\} \) の部分集合 \(W\) を言う。
-
\(D\) の \(X\)-\(Y\)-内部頂点切断とは、\(s\) から \(t\) への任意の路が \(W\) に属する頂点を少なくとも一つ含むような \(V\setminus\left( X\cup Y\right) \) の部分集合 \(W\) を言う。
この二つの定義は同じことを言っている。なぜなら:
-
\(V^{\prime}\setminus\left\{ s,t\right\} =V\setminus\left( X\cup Y\right) \) が成り立つ。
-
\(s\) から \(t\) への路と \(X\) から \(Y\) への路の間には全単射が存在する (実際、始点と終点を適切に置き換えれば両方向に変換できる)。この全単射は内部頂点を保存する (始点と終点以外の頂点が変化しない)。よって \(s\) から \(t\) への路 \(\mathbf{p}\) が \(W\) に属する頂点を少なくとも一つ含むのは、対応する \(X\) から \(Y\) への路 (この全単射による \(\mathbf{p}\) の像) が \(W\) に属する頂点を少なくとも一つ含むとき、かつそのときに限る。
よって、\(D^{\prime}\) の \(s\)-\(t\)-内部頂点切断は全て \(D\) の \(X\)-\(Y\)-内部頂点切断でもある。 ↩︎
-
-
証明: 次の二つの観察が分かる:
観察 1: \(k\) を自然数とする。\(D^{\prime}\) における \(s\) から \(t\) への路からなる任意の二要素が内部頂点素な \(k\) 要素集合が存在するなら、\(D\) における \(X\) から \(Y\) への路からなる任意の二要素が内部頂点素な \(k\) 要素集合が存在する。
[観察 1 の証明: \(D^{\prime}\) における \(s\) から \(t\) への路からなる任意の二要素が内部頂点素な \(k\) 要素集合が存在すると仮定する。これらの \(k\) 個の路はそれぞれ \(D\) における \(X\) から \(Y\) への路に「引き上げる」ことができる (弧はそのままにして、頂点 \(s\), \(t\) を弧と矛盾しないように \(X\) および \(Y\) に属する頂点にそれぞれ置き換える)。この「引き上げ」は路の内部頂点を変更しないので、こうして得られる \(k\) 個の路は任意の二つが内部頂点素である。よって \(D\) における \(X\) から \(Y\) への路からなる任意の二要素が内部頂点素な \(k\) 要素集合が存在する。]
観察 2: \(k\) を自然数とする。\(D\) における \(X\) から \(Y\) への路からなる任意の二要素が内部頂点素な \(k\) 要素集合が存在するなら、\(D^{\prime}\) における \(s\) から \(t\) への路からなる任意の二要素が内部頂点素な \(k\) 要素集合が存在する。
[観察 2 の証明: \(D\) における \(X\) から \(Y\) への路からなる任意の二要素が内部頂点素な \(k\) 要素集合が存在すると仮定する。これらの \(k\) 個の路からは (始点を \(s\) に、終点を \(t\) に置き換えることで) \(D^{\prime}\) における \(s\) から \(t\) への歩道からなる任意の二要素が内部頂点素な \(k\) 要素集合が得られる。任意の歩道は路を含み、歩道に含まれる路の内部頂点は元の歩道の内部頂点なので、\(D^{\prime}\) における \(s\) から \(t\) への路からなる任意の二要素が内部頂点素な \(k\) 要素集合も存在する。]
この二つの観察より、\(D^{\prime}\) における \(s\) から \(t\) への路からなる任意の二要素が内部頂点素な集合の最大要素数は、\(D\) における \(X\) から \(Y\) への路からなる任意の二要素が内部頂点素な集合の最大要素数に等しい。 ↩︎