10.3. 路残存集合

続いて、さらに人通りの少ない道へ進む。

Menger の定理 (の一つ) は 1927 年に発見され、Gallai–Milgram の定理は 1960 年に発見された。グラフの路に関する結果は遠い昔に全て発見されたのかと思った読者もいるかもしれない。

しかし、そうではないようだ。2017 年、本講義で課題として出すための練習問題を作るために、私は Python を使ってグラフの路に関する実験をしていた。具体的には、二つの異なる頂点 \(s\), \(t\) を持つ有向グラフ \(D=\left( V,A,\psi\right) \) を考えていた。弧に関する Menger の定理に発想を得て、\(s\) と \(t\) を切り離さずに (より正確に言えば、\(s\) から \(t\) への路の少なくとも一つを残すように) \(D\) から除去できる \(A\) の部分集合 \(B\) を調べる中で、そのような部分集合 \(B\) の個数は \(D\) が閉路あるいは「不用な弧」(\(s\) から \(t\) へのどの路にも含まれない弧) を持つとき偶数であり、そうでないとき奇数である¹ことに私は気が付いた。

この観察を私は証明できなかった。しかし、しばらくして Joel Brewster Lewis と Lukas Katthän が証明と複数のこれより強い結果を発見した。この証明は連名のプレプリント [GrKaLe21] から見ることができるものの、この結果は最適から程遠いと私は考えている (これはプレプリントをジャーナルに提出していない理由の一つである)。

私の観察に対する一つ目の改善は、偶奇性に関する主張を和に関する主張に書き換えることだった。これは「ある集合の要素数が偶数である」の形をした主張が「ある集合の要素それぞれにプラスまたはマイナスの符号を割り当てると、プラスの個数とマイナスの個数が一致する」の形をした主張になるという、一般的な現象の例と言える。改善された主張は次の通りである:

例 10.3.2

\(D=\left( V,A,\varphi\right) \) を次の有向グラフとする:

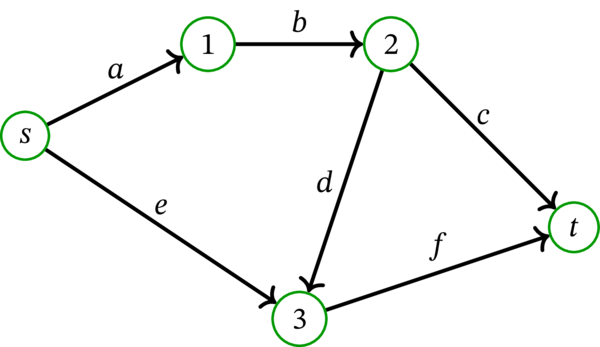
\(s\), \(t\) をそれぞれ上図で \(s\), \(t\) とラベルの付いた頂点とする。このとき \(D\) は閉路も「不要な弧」も持たず、\(A\) は空集合でない。よって定理 10.3.1 (d) が適用できる。\(A\) の路残存な部分集合は \(\left\{ a,b,c,d\right\} \), \(\left\{ c,e\right\} \), \(\left\{ d,e,f\right\} \) およびこれらの部分集合 (例えば \(\left\{ b,c,d\right\} \) など) である。言い換えれば、次の等式が成り立つ:

\[ \begin{aligned} \mathbf{M} &= \left\{ \left\{ a,b,c,d\right\} \text{ の部分集合} \right\} \cup \left\{ \left\{ c,e\right\} \text{ の部分集合} \right\} \cup \left\{ \left\{ d,e,f \right\} \text{ の部分集合} \right\} \\ & =\{\varnothing,\ \left\{ a\right\} ,\ \left\{ b\right\} ,\ \left\{ c\right\} ,\ \left\{ d\right\} ,\ \left\{ a,b\right\} ,\ \left\{ a,c\right\} ,\ \left\{ a,d\right\} ,\ \left\{ b,c\right\} ,\ \left\{ b,d\right\} ,\\ & \ \ \ \ \ \ \ \ \ \ \left\{ c,d\right\} ,\ \left\{ a,b,c\right\} ,\ \left\{ a,b,d\right\} ,\ \left\{ a,c,d\right\} ,\ \left\{ b,c,d\right\} ,\ \left\{ a,b,c,d\right\} ,\\ & \ \ \ \ \ \ \ \ \ \ \left\{ e\right\} ,\ \left\{ c,e\right\} ,\ \left\{ f\right\} ,\ \left\{ d,e\right\} ,\ \left\{ e,f\right\} ,\ \left\{ d,f\right\} ,\ \left\{ d,e,f\right\} \} \end{aligned} \]

よって和 \(\displaystyle \sum_{B\in\mathbf{M}}\left( -1\right) ^{\left\vert B\right\vert }\) における \((-1)^{\left\vert B\right\vert}\) は \(11\) 個の \(B\) で \(-1\) となり、\(12\) 個の \(B\) で \(1\) となる。ここから \(\displaystyle \sum_{B\in\mathbf{M}}\left( -1\right) ^{\left\vert B\right\vert } = 1\) が分かる。一方 \(\left( -1\right) ^{\left\vert A\right\vert -\left\vert V^{\prime}\right\vert }=\left( -1\right) ^{6-4}=1\) であり、定理 10.3.1 (d) が主張する等式は確かに成り立つ。

[定理 10.3.1 の証明] [GrKaLe21, Theorem 1.3] を見てほしい (この文献で \(\mathbf{M}\) は \(\operatorname*{PM}\left( D\right) \) と表記され、弧は辺と呼ばれる)。もちろん (c) は自明であり、(a) は難しくない (集合 \(B\in\mathbf{M}\) への不要な弧の追加もしくは集合 \(B\in\mathbf{M}\) からの弧の除去で得られる集合は必ず \(\mathbf{M}\) に属するため)。(b) と (d) は興味深くなる。[GrKaLe21, Theorem 1.3] の証明は「deletion-contraction」という再帰的な議論を用いている: \(s\) を始点に持つ弧 \(a\) を適当に選び、\(D\) から弧 \(a\) を除去 (delete) したグラフ \(D \setminus a\) と、\(D\) の弧 \(a\) を点に「縮約 (contract)」したグラフ \(D\diagup a\) という二つのグラフを考えるものである。

さらに強い命題は \(\mathbf{M}\) を位相空間とみなすことで得られる。実際、\(\mathbf{M}\) は適当な弧の集合ではなく、単体複体 (simplicial complex) と呼ばれる特徴を持つ集合である (\(B\) を \(A\) の路残存な部分集合とするとき、\(B\) の任意の部分集合もまた \(A\) の路残存な部分集合であるため)。単体複体は位相空間の組合せ論的モデルとして知られており、特にホモロジー群やホモトピー型を持つ。よって、単体空間 \(\mathbf{M}\) に対応する位相空間がどんなものかを考えることができる。この質問に対する答えも [GrKaLe21] で示されている: この位相空間は球面または球体 (閉路および「不用な弧」の有無によって決まる) にホモトピックであり、次元も明示的に計算できる (上述の \(\displaystyle \sum_{B\in\mathbf{M}}\left( -1\right) ^{\left\vert B\right\vert }\) は対応する位相空間の被約 Euler 標数に当然等しい)。