3.2. 単純グラフと多重グラフ間の変換
任意の多重グラフは単純グラフに変換できる。ただし、この変換では一部の情報が失われる:
\(G=\left( V,E,\varphi\right) \) を多重グラフとする。 \(G\) の台単純グラフ (underlying simple graph) \(G^{\operatorname*{simp}}\) とは、次の単純グラフを意味する:
言い換えれば、\(G^{\operatorname*{simp}}\) の頂点集合は \(G\) と同じ \(V\) であり、\(G^{\operatorname*{simp}}\) の異なる二頂点 \(u\), \(v\) は \(G\) で隣接するとき、かつそのときに限って隣接する。つまり、\(G^{\operatorname*{simp}}\) は \(G\) からループを除去して平行な辺を一つに「まとめる」ことで得られる。
例えば、例 3.1.3 で示した多重グラフの台単純グラフは次のグラフである:
逆に、単純グラフを多重グラフとみなすこともできる:
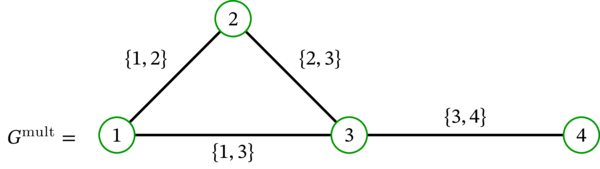
\(G=\left( V,E\right) \) を単純グラフとする。次の多重グラフを \(G\) の対応多重グラフ (corresponding multigraph) と呼び、\(G^{\operatorname*{mult}}\) と表記する:
ここで \(\iota\colon E\rightarrow\mathcal{P}_{1,2}\left( V\right) \) は \(e \in E\) を \(e\) 自身に対応させる写像である。
次の単純グラフを \(G\) とする:
このとき \(G^{\operatorname*{mult}}\) は次の多重グラフとなる:
上述したように台単純グラフの構築 \(G\mapsto G^{\operatorname*{simp}}\) は情報を喪失させるので、不可逆である。ただ、\(G\mapsto G^{\operatorname*{simp}}\) と \(G\mapsto G^{\operatorname*{mult}}\) は正反対の変換に近く、特定の条件下では実際に正反対となる1:
-
\(G\) が単純グラフなら \(\left( G^{\operatorname*{mult}}\right) ^{\operatorname*{simp}}=G\) が成り立つ。
-
\(G\) がループと平行辺を持たない多重グラフなら \(\left( G^{\operatorname*{simp}}\right) ^{\operatorname*{mult}}\cong G\) が成り立つ。
-
\(G\) がループまたは平行辺を持つ多重グラフなら、多重グラフ \(\left( G^{\operatorname*{simp}}\right) ^{\operatorname*{mult}}\) は \(G\) より少ない辺を持ち、そのため \(G\) と同型でない。
定義を理解できたかどうかの問題である。□
単純グラフ \(G\) と \(G\) の対応多重グラフ \(G^{\operatorname*{mult}}\) を同一視する場合がよくある。これは危険に思える: 隣接性・歩道・路・閉路といった概念は単純グラフと多重グラフの両方に定義されているので、\(G\) と \(G^{\operatorname*{mult}}\) を同一視すると文が曖昧になる可能性がある。 幸い、この曖昧性に危険はない。なぜなら、\(G\) が単純グラフのとき、これまで本書で \(G\) に対して定義してきた全ての概念は多重グラフ \(G^{\operatorname*{mult}}\) に対する同名の概念と等価だからである。例えば閉路という概念に対しては、次の命題が成り立つ:
\(G\) を単純グラフとする。このとき:
-
\(\left( v_{0},e_{1},v_{1},e_{2},v_{2},\ldots ,e_{k},v_{k}\right) \) が多重グラフ \(G^{\operatorname*{mult}}\) の閉路なら、\(\left( v_{0},v_{1},\ldots,v_{k}\right) \) は単純グラフ \(G\) の閉路である。
-
逆に、\(\left( v_{0},v_{1},\ldots,v_{k}\right) \) が単純グラフ \(G\) の閉路なら、\(( v_{0},\left\{ v_{0},v_{1}\right\} ,v_{1},\left\{ v_{1},v_{2}\right\} ,v_{2},\ldots,\) \(v_{k-1}\left\{ v_{k-1},v_{k}\right\} ,v_{k}) \) は多重グラフ \(G^{\operatorname*{mult}}\) の閉路である。
単純グラフと閉路と多重グラフの閉路は定義が少しだけ異なるので、この命題は完全に自明なわけではない。非自明なのは次の二点である:
-
\(\left( v_{0},e_{1},v_{1},e_{2},v_{2},\ldots,e_{k},v_{k}\right) \) が多重グラフ \(G^{\operatorname*{mult}}\) の閉路なら、\(k \geq 3\) が成り立つ。
-
\(\left( v_{0},v_{1},\ldots,v_{k}\right) \) が単純グラフ \(G\) の閉路なら、その辺 \(\left\{ v_{0},v_{1}\right\}\), \(\left\{ v_{1},v_{2}\right\}\), ..., \(\left\{ v_{k-1},v_{k}\right\} \) は相異なる。
一つ目の命題は易しい: \(G^{\operatorname*{mult}}\) はループを持たないので \(k \neq 1\) が分かる。また、\(k=2\) だと \(e_{1} = e_{2}\) となって考えている列が閉路でなくなるので \(k \neq 2\) も分かる。二つ目の命題も難しくない: \(G\) の閉路 \(\left( v_{0},v_{1},\ldots,v_{k}\right) \) に含まれる \(k\) 個の頂点 \(v_{0},v_{1},\ldots,v_{k-1}\) は相異なるので、\(k\) 個の二要素集合 \(\left\{ v_{0},v_{1}\right\} ,\left\{ v_{1},v_{2}\right\} ,\ldots,\left\{ v_{k-1},v_{k}\right\} =\left\{ v_{k-1},v_{0}\right\} \) も相異なる。□
本書でこれまでに議論した他の概念で曖昧性が生じないことは、ここで見た閉路以上に明らかである。