3.1. 多重グラフの定義

ここまでは単純グラフだけを考えてきた。以降では単純グラフと異なる種類のグラフをいくつか定義する。最初に定義されるのは多重グラフである:

定義 3.1.1

集合 \(V\) に対して、要素数が \(1\) または \(2\) であるような \(V\) の部分集合全体の集合を \(\mathcal{P}_{1,2}\left( V\right) \) と表す。言い換えれば、次のように定める:

\[ \begin{aligned} \mathcal{P}_{1,2}\left( V\right) \colonequals & \left\{ S\subseteq V\ \mid \ \left\vert S\right\vert \in\left\{ 1,2\right\} \right\} \\ = & \left\{ \left\{ u,v\right\} \mid u,v\in V\ \left(u=v\text{ でも構わない}\right)\right\} \end{aligned} \]

例えば、次の等式が成り立つ:

\[ \mathcal{P}_{1,2}\left( \left\{ 1,2,3\right\} \right) =\left\{ \left\{ 1\right\} ,\ \left\{ 2\right\} ,\ \left\{ 3\right\} ,\ \left\{ 1,2\right\} ,\ \left\{ 1,3\right\} ,\ \left\{ 2,3\right\} \right\} \]

\(\mathcal{P}_{1,2}(V)\) を使って多重グラフを定義する:

定義 3.1.2

二つの有限集合 \(V\), \(E\) と写像 \(\varphi\colon E\rightarrow\mathcal{P}_{1,2}\left( V\right) \) からなる三つ組 \(\left( V,E,\varphi\right) \) を多重グラフ (multigraph) と呼ぶ。

例 3.1.3

多重グラフの例を示す:

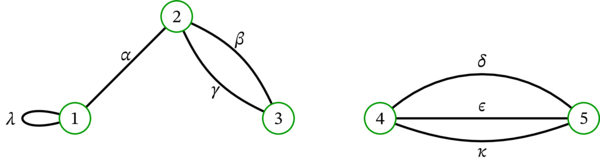
数式で書くなら、この多重グラフは \(\left( V,E,\varphi\right) \) と書ける。ここで

\[ V=\left\{ 1,2,3,4,5\right\} ,\quad E=\left\{ \alpha,\beta,\gamma,\delta,\varepsilon,\kappa,\lambda\right\} \]

であり、\(\varphi\colon E\rightarrow\mathcal{P}_{1,2}\left( V\right) \) は \(\alpha\), \(\beta\), \(\gamma\), \(\delta\), \(\varepsilon\), \(\kappa\), \(\lambda\) をそれぞれ \(\left\{ 1,2\right\}\), \(\left\{ 2,3\right\}\), \(\left\{ 2,3\right\}\), \(\left\{ 4,5\right\}\), \(\left\{ 4,5\right\}\), \(\left\{ 4,5\right\}\), \(\left\{ 1\right\} \) に移す写像である。 [もちろん、\(\left\{ 1\right\} \) を \(\left\{ 1,1\right\} \) と書いても構わない。]

多重グラフの定義から、多重グラフに対する次の用語が自然に定義される。ほとんどは単純グラフに対して定義される用語と同様の意味を持つ:

定義 3.1.4

\(G=\left( V,E,\varphi\right) \) を多重グラフとする。

\(V\) の要素を \(G\) の頂点 (vertex) と呼ぶ。\(V\) を \(G\) の頂点集合 (vertex set) と呼び、\(\operatorname*{V}\left( G\right) \) と表記する。
\(E\) の要素を \(G\) の辺 (edge) と呼ぶ。\(E\) を \(G\) の辺集合 (edge set) と呼び、\(\operatorname*{E}\left( G\right) \) と表記する。
\(G\) の辺 \(e\) に対して、\(\varphi\left( e\right) \) の要素を \(e\) の端点 (endpoint) と呼ぶ。
辺 \(e\) が頂点 \(v\) を含む (contain)とは、\(v\in\varphi\left( e\right) \) が成り立つ (言い換えれば、\(v\) が \(e\) の端点である) ことを言う。
二頂点 \(u\), \(v\) が隣接する (adjacent) とは、端点が \(u\) と \(v\) の辺 \(e \in E\) が存在することを言う。
二辺 \(e\), \(f\) が平行 (parallel) とは、\(\varphi\left( e\right) =\varphi\left( f\right) \) を満たすことを言う。
\(G\) の任意の相異なる二辺が平行でないとき、\(G\) は平行辺を持たないと言う。
辺 \(e\) がループ (loop) とは、\(\varphi\left( e\right) \) が単元集合 (\(e\) の端点が一つだけ) であることを言う。ループは自己ループ (self-loop) とも呼ばれる。 [例 3.1.3 の多重グラフでは \(\lambda\) がループである。]
\(G\) がループレス (loopless) とは、ループである辺を \(G\) が持たないことを言う。
\(G\) の頂点 \(v\) の次数 (degree) \(\deg v\) とは、\(v\) を含む辺の個数を言う。ただしループは二回カウントする。言い換えれば、次のように定める:

\[ \begin{aligned} \deg v = & \deg_{G}v\\ \colonequals & \underbrace{\left\vert \left\{ e\in E\mid v\in\varphi\left( e\right) \right\} \right\vert }_{\substack{v \text{ を含む辺の個数を数える}}}+\underbrace{\left\vert \left\{ e\in E\mid \varphi\left( e\right) =\left\{ v\right\} \right\} \right\vert }_{\substack{v \text{ を含むループをもう一度数える}}} \end{aligned} \]

上式でも使われているように、\(\deg v\) は \(\deg_{G} v\) とも書く。

[単純グラフと異なり、多重グラフでは頂点 \(v\) の次数が \(v\) の隣接頂点の個数と異なる点に注意してほしい。\(v\) がループと平行辺をどちらも持たないときに限って両者は等しくなる。]

[例えば、例 3.1.3 の多重グラフでは \(\deg1 = 3\), \(\deg2 = 3\), \(\deg3 = 2\), \(\deg4 = 3\), \(\deg5 = 3\) が成り立つ。]
\(G\) における歩道 (walk) とは、次の形をした列を言う:

\[ \left( v_{0},e_{1},v_{1},e_{2},v_{2},\ldots,e_{k},v_{k}\right) \quad \left(k\geq0\right) \]

ここで \(v_{0},v_{1},\ldots,v_{k}\) は \(G\) の頂点、\(e_{1},e_{2},\ldots,e_{k}\) は \(G\) の辺であり、次の条件が全ての \(i\in\left\{ 1,2,\ldots,k\right\} \) で成り立つ:

\[ \varphi\left( e_{i}\right) =\left\{ v_{i-1},v_{i}\right\} \]

[つまり、\(e_{i}\) の端点が \(v_{i-1}\) と \(v_{i}\) である必要がある。なお、歩道に頂点と辺が両方とも含まれるのは、二頂点間を「移動」するときに使う辺を歩道から分かるようにするためである。例えば例 3.1.3 の多重グラフでは、\(\left( 1,\alpha,2,\beta,3\right) \) と \(\left( 1,\alpha,2,\gamma,3\right) \) は二つの異なる歩道を表す。]

歩道 \(\left( v_{0},e_{1},v_{1},e_{2},v_{2},\ldots,e_{k},v_{k}\right) \) の頂点 (vertex) とは \(v_{0},v_{1},\ldots,v_{k}\) を指し、この歩道の辺 (edge) とは \(e_{1},e_{2},\ldots,e_{k}\) を指す。また、この歩道は \(v_{0}\) から始まり、\(v_{k}\) で終わると言う。さらに、この歩道を \(v_{0}\) から \(v_{k}\) への歩道 (walk from \(v_{0}\) to \(v_{k}\)) と呼ぶ。この歩道の始点 (starting point) とは \(v_{0}\) を指し、終点 (ending point) とは \(v_{k}\) を指す。
頂点が全て異なる歩道を路 (path) と呼ぶ。
路連結 (path-connected)、連結 (connected)、成分 (component) は単純グラフと同様に定義される。記号 \(\simeq_{G}\) は多重グラフでも路連結性を表すのに使われる。
\(v_{k}=v_{0}\) を満たす歩道 \(\left( v_{0},e_{1},v_{1},e_{2},v_{2},\ldots,e_{k},v_{k}\right) \) を閉歩道 (closed walk) と呼ぶ。閉歩道は回路 (circuit) とも呼ばれる。
次の条件を満たす閉歩道 \(\left( v_{0},e_{1},v_{1},e_{2},v_{2},\ldots,e_{k},v_{k}\right) \) を閉路 (cycle) と呼ぶ:
- 頂点 \(v_{0},v_{1},\ldots,v_{k-1}\) が相異なる。
- 辺 \(e_{1},e_{2},\ldots,e_{k}\) が相異なる。
- \(k \geq 1\) が成り立つ。
[単純グラフの閉路に存在した \(k \geq 3\) という条件は多重グラフの閉路には存在しない。そのため例 3.1.3 の多重グラフでは \(\left( 2,\beta ,3,\gamma,2\right) \) と \(\left( 1,\lambda,1\right) \) がどちらも閉路となる。一方で \(\left( 2,\beta,3,\beta,2\right) \) は閉路でない。単純グラフの閉路に対する \(k \geq 3\) の条件は \(\left( 2,\beta,3,\beta,2\right) \) のような歩道を閉路としないために存在していた。多重グラフでは「\(e_{1},e_{2},\ldots,e_{k}\) が相異なる」の条件によってそのような歩道が閉路から除外されるので、\(k\geq3\) の条件は必要ない。]
ハミルトン路 (Hamiltonian path)とハミルトン閉路 (Hamiltonian cycle) は単純グラフと同様に定義される。
多重グラフの描画では頂点を点として、辺を曲線として描き、頂点と辺の両方にラベルを付ける (頂点や辺を区別しないときはラベルを省略する場合もある)。例 3.1.3 で示したのは多重グラフの描画である。

単純グラフと多重グラフには、二つの重要な違いがある:

多重グラフはループを持てるのに対して、単純グラフはループを持てない。
単純グラフでは、頂点からなる二要素集合が辺 \(e\) に等しい。これに対して多重グラフでは、頂点からなる要素数が \(1\) (辺がループのとき) または \(2\) の集合を辺 \(e\) が持つ: 写像 \(\varphi\) が辺に集合を割り当てる。これによって平行辺の存在が許されるだけではなく、辺の「識別子」に何らかの情報を格納できるようにもなる。

ただ、単純グラフと多重グラフには共通点も多くある。そのため両方とも「グラフ」と呼ばれる:

慣習 3.1.5

「グラフ」という単語は「単純グラフ」と「多重グラフ」のいずれかを意味する。どちらを意味するかは文脈から通常は理解できる。 [本書では、混同を招きかねない状況で「グラフ」という単語を使わないようにする。]

幸い、単純グラフと多重グラフの両方で成り立つ性質は数多く存在し、多重グラフの結果から単純グラフに関する同様の結果を容易に導ける場合もしばしばある。これから本章では、前章で見た単純グラフに対する性質の一部が多重グラフでも考えられることを見ていく。ただまずは、多重グラフを単純グラフに (そして単純グラフを多重グラフに) 変換する方法を説明する。