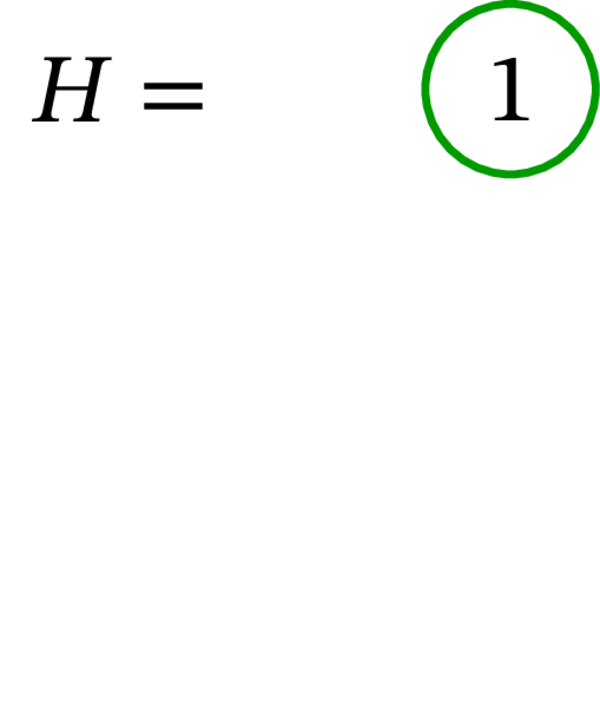3.4. オイラー歩道とオイラー回路

3.4.1定義

続いて多重グラフの新しい性質を紹介する。この性質は本書で初めて登場する (単純グラフに対しては考えてこなかった)。

ハミルトン (閉) 路とは、グラフの全ての頂点を含む (閉) 路を言うのだった。路と閉路の定義より、ハミルトン (閉) 路はグラフの全ての頂点をちょうど一度ずつ含む (ただしハミルトン閉路では始点と終点だけが一致する)。

では、グラフの全ての辺を含む歩道あるいは閉歩道を考えてもいいのではないだろうか？ これはオイラー歩道あるいはオイラー回路と呼ばれる概念であり、数学的には次のように定義される:

ハミルトン (閉) 路と異なり、オイラー歩道とオイラー回路は一般に路あるいは閉路とならない。[しかし、文献によってはオイラー歩道が「オイラー路」と呼ばれたり、オイラー回路が「オイラー閉路」と呼ばれたりすることがある。これは混乱を招くだけなので望ましくない。] また、多重グラフ \(G\) のオイラー歩道を見つける問題は単純グラフ \(G^{\operatorname*{simp}}\) でオイラー歩道を見つける問題と同じではない。

例 3.4.2

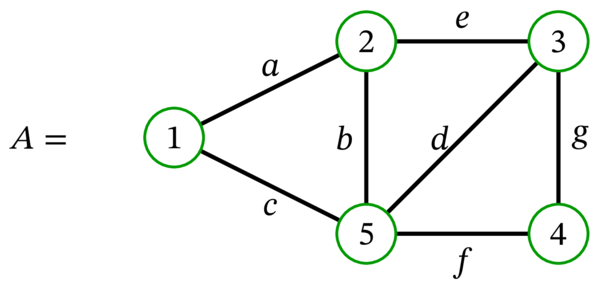
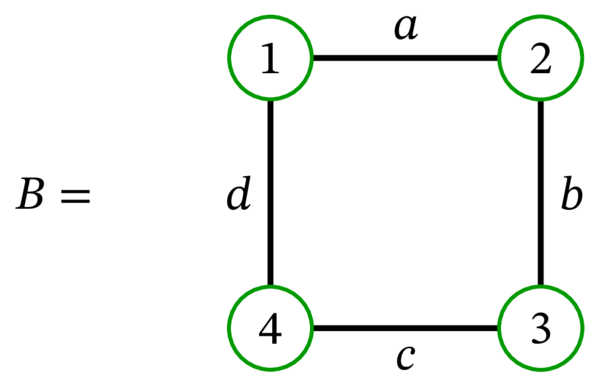
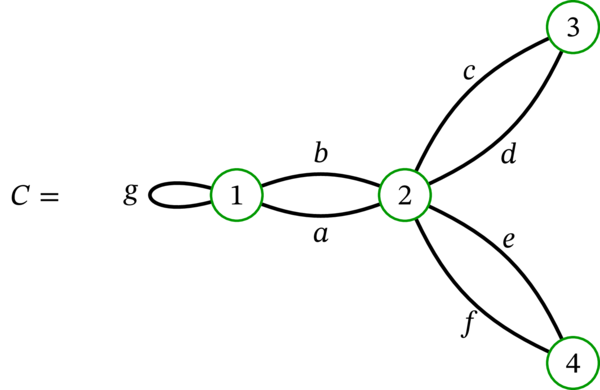
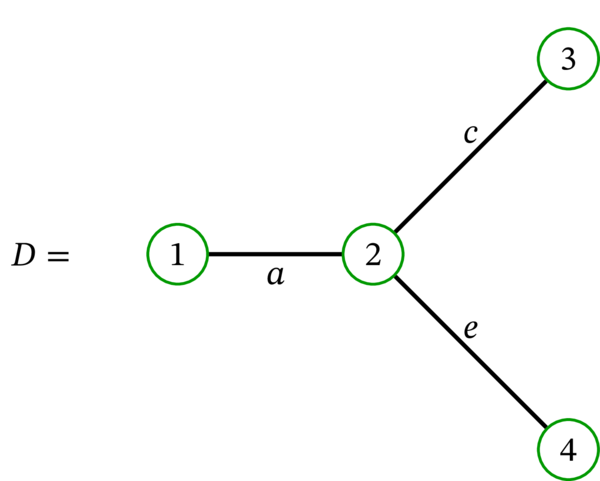
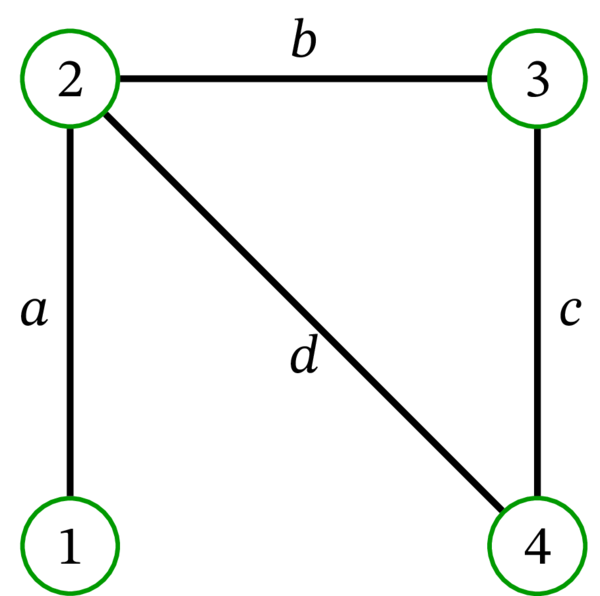
次の多重グラフを考える:

• 多重グラフ \(A\) はオイラー歩道 \(\left( 3,d,5,b,2,e,3,g,4,f,5,c,1,a,2\right) \) を持つ。しかし \(A\) はオイラー回路を持たない。\(A\) がオイラー回路を持たない事実は、次数が奇数の頂点 \(2\) が \(A\) に存在する事実に注目すると納得できる。もしオイラー回路が存在するなら、そのオイラー回路は \(2\) に入るのと同じ回数だけ \(2\) から出る必要がある。しかしそのとき頂点 \(2\) の次数は偶数となる (オイラー回路では \(2\) を含む全ての辺が \(2\) に入るか \(2\) から出るのにちょうど一回ずつ利用されるため。例外的にループは二回使われるものの、次数の偶奇性には影響しない)。一般に、次数が奇数の頂点を持つ多重グラフにオイラー回路は存在しない。

• 多重グラフ \(B\) はオイラー回路 \(\left( 1,a,2,b,3,c,4,d,1\right) \) を持つ。よって \(B\) はオイラー歩道も持つ (任意のオイラー回路はオイラー歩道であるため)。

• 多重グラフ \(C\) はオイラー回路 \(\left( 1,g,1,b,2,c,3,d,2,e,4,f,2,a,1\right) \) を持つ。

• 多重グラフ \(D\) はオイラー歩道を持たない。実際、\(D\) には次数が奇数の頂点が \(4\) 個存在する。グラフの頂点 \(v\) が奇数の次数を持つとき、任意のオイラー歩道は \(v\) を始点または終点として持たなければならない (そうでなければオイラー歩道が \(v\) に入る回数と \(v\) から出る回数が一致するので \(v\) の次数が偶数となる)。しかし歩道は始点と終点を一つずつしか持てないので、オイラー歩道を持つグラフに含まれる次数が奇数の頂点は最大でも二個だと分かる。一般に、次数が奇数の頂点を \(3\) 個以上持つグラフはオイラー歩道を持たない。

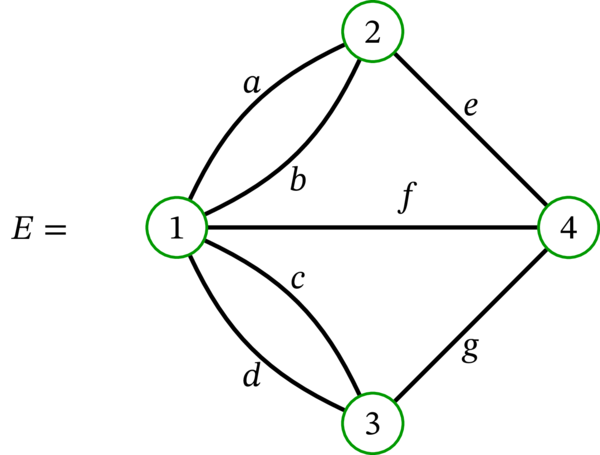
• 多重グラフ \(E\) はオイラー歩道を持たない。これは \(D\) と同じ理由で分かる。なお、\(E\) は Euler が 1736 年の論文で考えたケーニヒスベルクの橋に関連する有名な多重グラフである (「ケーニヒスベルクの七つの橋」のエピソードについては Wikipedia を参照してほしい)。

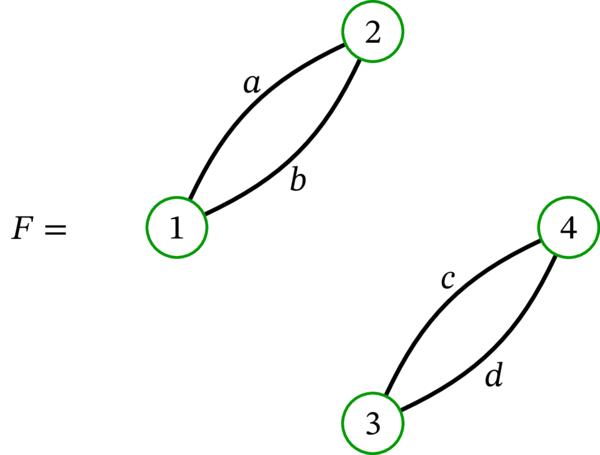
• 多重グラフ \(F\) はオイラー歩道を持たない。\(F\) が二つの成分を持ち、それぞれの成分が一個以上の辺を持つためである (オイラー歩道は \(b\) と \(c\) を含まなければならないものの、この二辺は属する成分が異なるので一つの歩道でつなぐことができない)。

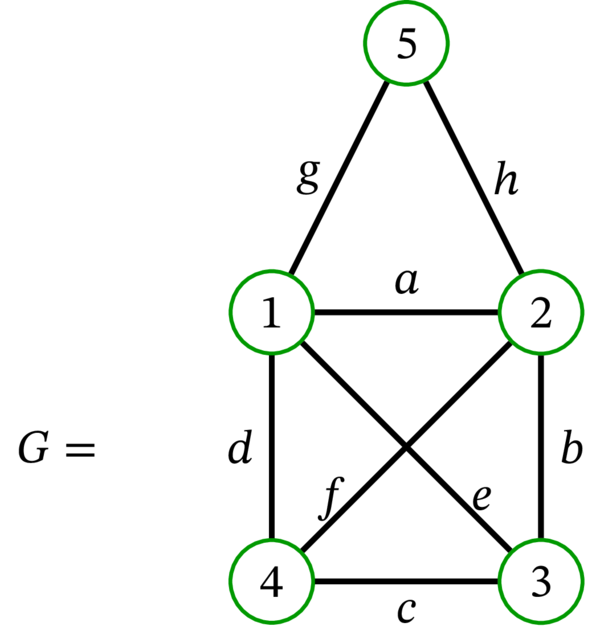
• 多重グラフ \(G\) はオイラー歩道 \(\left( 3,b,2,h,5,g,1,a,2,f,4,d,1,e,3,c,4\right) \) を持つ。しかし次数が奇数の頂点が二個存在するので、オイラー回路は \(G\) に存在しない。

• 多重グラフ \(H\) はオイラー回路 \(\left( 1\right) \) を持つ。

Remark 3.4.3

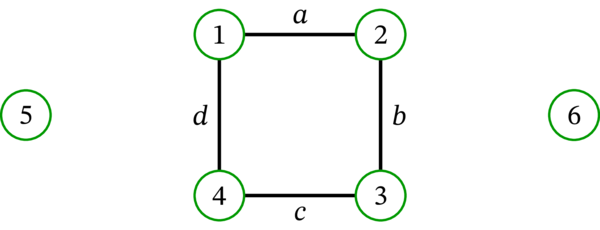
目ざとい読者へ: 多重グラフが連結でなかったとしても、全ての辺が一つの成分に属する (一つの成分を除く全ての成分が頂点だけからなる) ならオイラー回路が存在する可能性はある。例えば次のグラフはオイラー回路を持つ:

3.4.2Euler–Hierholzer の定理

多重グラフのオイラー歩道あるいはオイラー回路を見つける問題、そしてオイラー歩道あるいはオイラー回路の存在を判定する問題はどれくらい難しいのだろうか？ 意外なことに、これらの問題はハミルトン (閉) 路に対する同様の問題よりずっと簡単なことが分かっている。例えば、次の Euler–Hierholzer の定理 (Euler–Hierholzer theorem) を使うと (連結な多重グラフに対する) 二つ目の問題に答えられる:

両方の命題の \(\Longrightarrow\) 方向は 例 3.4.2 の \(A\) と \(D\) に関する考察で示した。これから \(\Longleftarrow\) 方向を証明する。私の知る限り Euler が 1736 年に公開した論文はこちらの方向の命題を証明しておらず、実際に証明したのは Hierholzer が 1873 年に公開した論文だった。この命題の「標準的な」証明は多くの教科書 (例えば [Guicha16, Theorem 5.2.2 and Theorem 5.2.3]) に載っている。ここには標準的でない証明の概略を示す。この証明を私は [LeLeMe18, Problem 12.35] から学んだ。まず、次の定義が必要になる:

つまり小道は重複する頂点を持つことができるものの、重複する辺は許されない。

オイラー歩道は必ず小道となる。また、オイラー歩道より長い小道は存在しない。よってオイラー歩道を構築する自然な方法は「適当な小道から始めて、オイラー歩道になるまでそれを長くし続ける」となる。

ここから、定理 3.4.4 の \(\Longleftarrow\) 方向を証明するアプローチが一つ示唆される: \(G\) で最も長い小道を取り、それがオイラー歩道でなければ長くできてしまうと示せばよい。もちろん、どうやって「長く」するのかを説明する必要がある。最初のステップは次の命題である:

[証明] \(G\) は明らかに小道を一つ持つ (例えば任意の頂点一つだけからなる長さ \(0\) の小道がある)。さらに、\(G\) の小道は有限個しか存在しない (小道では \(G\) の各辺を最大でも一度しか使えず、\(G\) の辺は有限個しか存在しないため)。よって最大値原理より \(G\) は最長の小道を持つ。□

これからの目標は「適切な条件の下では最長の小道がオイラー歩道となる」ことの証明である。このためには、さらに二つの補題が必要になる。

まず、用語を一つ定める: \(G\) を多重グラフ、\(e\) を \(G\) の辺、\(\mathbf{w}\) を \(G\) の歩道とする。\(e\) の端点の少なくとも一つが \(\mathbf{w}\) の頂点であるとき、辺 \(e\) と歩道 \(\mathbf{w}\) は交わる (intersect) と言う。辺 \(e\) と歩道 \(\mathbf{w}\) が交わる例を次に示す:

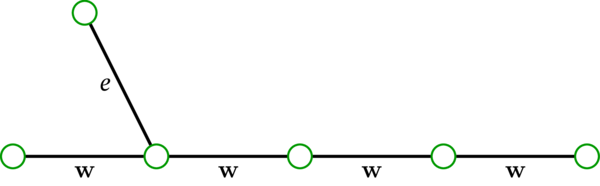
[辺に付いている "\(\mathbf{w}\)" は \(\mathbf{w}\) の辺であることを表す。] 次の図でも辺 \(e\) と歩道 \(\mathbf{w}\) が交わる。この状況では \(e\) の端点がたまたま \(\mathbf{w}\) の始点と等しい:

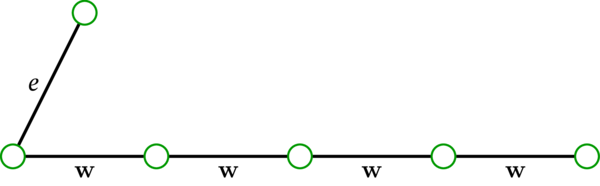
さらに次の図でも辺 \(e\) と歩道 \(\mathbf{w}\) が交わる。ここでは \(e\) の端点が両方とも \(\mathbf{w}\) に含まれる:

ここに示した図から \(\mathbf{w}\) に関して誤解をしないように注意してほしい。\(\mathbf{w}\) は歩道なので、任意の頂点を何度でも通ることができる！

[証明] 補題の仮定より \(\mathbf{w}\) の辺でない \(G\) の辺が存在する。そのような辺を一つ取って \(f\) とする。

\(\mathbf{w}\) の頂点から \(f\) の端点への路を「\(\mathbf{w}\)-\(f\) 路」と呼ぶことにする。\(G\) は連結なので、\(\mathbf{w}\)-\(f\) 路は明らかに存在する。\(\mathbf{w}\)-\(f\) 路の中で長さが最小のものを \(\mathbf{p}\) とする。\(\mathbf{p}\) の長さが \(0\) なら \(f\) と \(\mathbf{w}\) は交わるので、証明が完了する。そうでなく \(\mathbf{p}\) の長さが \(0\) より大きいなら、\(\mathbf{p}\) の最初の辺 \(e\) に注目する。\(e\) は \(\mathbf{w}\) に含まれない: もし含まれるなら \(\mathbf{p}\) から \(e\) を取り除くことで \(\mathbf{p}\) より短い \(\mathbf{w}\)-\(f\) 路が得られるものの、これは \(\mathbf{p}\) の最小性に反する。一方で \(e\) は明らかに \(\mathbf{w}\) と交わる。つまり \(e\) は \(\mathbf{w}\) の辺でなくて \(\mathbf{w}\) と交わる。以上で補題は証明された。□

[証明] 背理法で示す。\(\mathbf{w}\) が閉歩道でないと仮定する。\(\mathbf{w}\) の始点と終点をそれぞれ \(u\), \(v\) とすれば、この仮定より \(u\neq v\) が成り立つ。

\(v\) を含む \(\mathbf{w}\) の辺を考える。そのような辺は「\(\mathbf{w}\) で \(v\) に入る (自身の直後に \(v\) がある)」と「\(\mathbf{w}\) で \(v\) から出る (自身の直前に \(v\) がある)」の少なくとも一方を満たす¹。\(\mathbf{w}\) の最後の辺を除けば、前者の性質を持つ辺の次には後者の性質を持つ辺が続く。一方、後者の性質を持つ辺の一つ前には必ず前者の性質を持つ辺がある (\(\mathbf{w}\) の始点 \(u\) は \(v\) と異なるため)。よって \(\mathbf{w}\) は \(v\) に入る辺を \(v\) に出る辺より一つだけ多く持つ。つまり、\(v\) を含む \(\mathbf{w}\) の辺の個数 (ループは二度数える) は奇数である。補題の仮定より \(v\) の次数は偶数なので、\(G\) 全体を考えたときの \(v\) を含む辺の個数 (ループは二度数える) は偶数であり、両者は異なる。よって \(G\) には \(v\) を含み \(\mathbf{w}\) に含まれない辺が少なくとも一つ存在する。

そのような辺を一つ取って \(f\) とする。\(f\) を小道 \(\mathbf{w}\) に加えて得られる歩道は (\(f\) が \(\mathbf{w}\) の辺でないことから) 小道であり、\(\mathbf{w}\) より長い。これは \(\mathbf{w}\) が最長の小道である事実と矛盾する。よって補題は証明された。□

この二つの補題を使うと、Euler–Hierholzer の定理を完全に証明できる:

[定理 3.4.4 の証明] (a) \(\Longrightarrow\): 例 3.4.2 で示した。

(a) \(\Longleftarrow\): \(G\) の各頂点が偶数の次数を持つと仮定する。

補題 3.4.6 より \(G\) は最長の小道 \(\mathbf{w}\) を持つ。補題 3.4.8 からは \(\mathbf{w}\) が閉歩道だと分かる。

\(\mathbf{w}\) がオイラー回路だと背理法で示す。\(\mathbf{w}\) がオイラー回路でないと仮定する。このとき \(\mathbf{w}\) に含まれない \(G\) の辺が存在する。補題 3.4.7 より、\(G\) には \(\mathbf{w}\) に含まれず \(\mathbf{w}\) と交わる辺が存在する。そのような辺を一つ取って固定し、\(f\) とする。

\(f\) は \(\mathbf{w}\) と交わるので、\(\mathbf{w}\) の頂点である \(f\) の端点 \(v\) が存在する。\(\mathbf{w}\) は閉歩道だから、一般性を失うことなく \(\mathbf{w}\) は \(v\) から始まって \(v\) で終わると仮定できる (こうなるまで \(\mathbf{w}\) を回転²させればよい)。このとき小道 \(w\) の末尾に \(f\) を追加した歩道を考える。\(f\) は \(\mathbf{w}\) に含まれないので、この歩道は小道である。また、この歩道は \(\mathbf{w}\) よりも長い。これは \(\mathbf{w}\) が \(G\) の最長の小道である仮定と矛盾する。

この矛盾から \(\mathbf{w}\) はオイラー回路だと分かる。以上で定理 3.4.4 (a) の \(\Longleftarrow\) 方向が証明された。

(b) \(\Longrightarrow\): 例 3.4.2 で示した。

(b) \(\Longleftarrow\): 奇数の次数を持つ \(G\) の頂点の個数が最大でも \(2\) だと仮定する。このとき \(G\) がオイラー歩道を持つと示す必要がある。

もし \(G\) の全ての頂点が偶数の次数を持つなら、この事実は定理 3.4.4 (a) から従う (任意のオイラー回路はオイラー歩道でもあるため)。よって以降では一般性を失うことなく次数が奇数の頂点が \(G\) に存在すると仮定する。

多重グラフに対する握手補題 (補題 3.3.3) より、奇数の次数を持つ \(G\) の頂点の個数は偶数である。また、その個数が \(2\) 以下であることも問題の仮定から分かる。つまり奇数の次数を持つ \(G\) の頂点の個数は偶数かつ \(1\) 以上 \(2\) 以下なので、\(2\) と結論できる。これらの頂点を \(u\), \(v\) とする。

\(u\) と \(v\) を結ぶ新しい辺 \(e\) を \(G\) に追加して得られるグラフを \(G^{\prime}\) とする³ (\(G\) は多重グラフなので、\(u\) と \(v\) を結ぶ辺が既に存在する場合でもこの辺は追加できる！)。新しく追加した辺 \(e\) は \(u\) と \(v\) の次数を \(1\) ずつ増やすので、\(G^{\prime}\) の全ての頂点は偶数の次数を持つ。さらに、\(G\) は連結より \(G^{\prime}\) も連結と分かる。したがって \(G^{\prime}\) には定理 3.4.4 (a) を適用できる: \(G^{\prime}\) はオイラー回路を持つ。このオイラー回路から \(e\) を取り除けば⁴ \(G\) のオイラー歩道が得られる。\(G\) がオイラー歩道を持つことが示せたので、以上で 定理 3.4.4 (b) の \(\Longleftarrow \) 方向は証明された。□

Note: 上の証明を注意深く観察すると、グラフのオイラー回路またはオイラー歩道を構築するアルゴリズムが得られる⁵。

練習問題 3.15

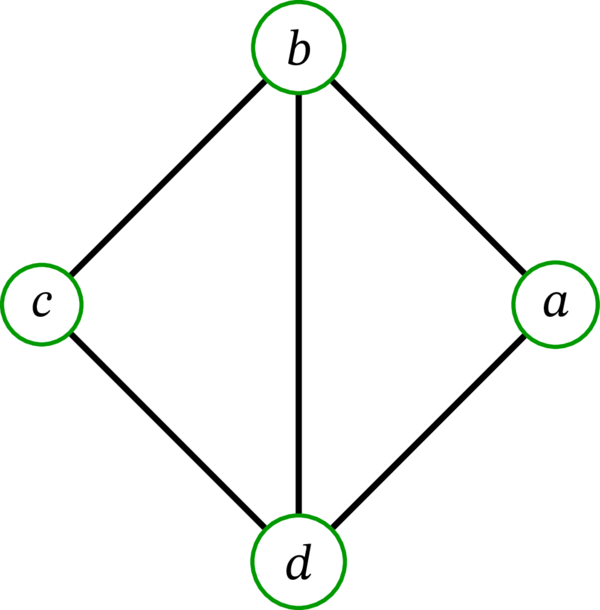
\(G=\left( V,E,\varphi\right) \) を多重グラフとする。線グラフ (line graph) \(L\left( G\right) \) とは、次の条件を満たす単純グラフ \(\left( E,F\right) \) を言う:

\[ F=\left\{ \left\{ e_{1},e_{2}\right\} \in\mathcal{P}_{2}\left( {E}\right) \mid \varphi\left( e_{1}\right) \cap\varphi\left( e_{2}\right) \neq\varnothing\right\} \]

[言い換えれば: \(L\left( G\right) \) の頂点は \(G\) の辺であり、\(L(G)\) の二頂点 \(e_{1}\), \(e_{2}\) は \(G\) で両者が端点を共有するとき、かつそのときに限って隣接する。]

[例: 多重グラフ \(G\) と \(G\) の線グラフ \(L\left(G\right)\) の例を次に示す:

例えば、辺 \(a\), \(d\) は \(G\) で端点 \(2\) を共有するので、\(G\) の線グラフ \(L(G)\) で頂点 \(a\), \(d\) は隣接する。]

\(\left\vert V\right\vert >1\) と仮定する。次の命題を示せ:

1. \(G\) がハミルトン路を持つなら、\(L\left( G\right) \) はハミルトン路を持つ。

2. \(G\) がオイラー歩道を持つなら、\(L\left( G\right) \) はハミルトン路を持つ。

[解答: これは 2017 年春学期に開講された講義で出した midterm #1 の Exercise 2 (を多重グラフに一般化したもの) である。解答は講義ページに載っている。]