3.3. 単純グラフから多重グラフへの一般化
それでは先述したように、第 2 章で示した単純グラフに関する様々な結果が多重グラフでも成り立つかどうかを見ていこう。
3.3.1 ラムゼー数 \(R\left( 3,3\right)\)
本書で最初に証明した単純グラフの性質の一つは次の命題 (定理 2.3.1) だった:
\(G\) は単純グラフで \(\left| \operatorname{V}\left( G \right) \right| \geq6\) を満たすとする (つまり、\(G\) は \(6\) 個以上の頂点を持つとする)。このとき、次の二つの命題の少なくとも一方が成り立つ:
-
命題 1: 辺 \(ab\), \(bc\), \(ca\) が全て \(G\) に存在するような \(G\) の頂点 \(a\), \(b\), \(c\) が存在する。
-
命題 2: 辺 \(ab\), \(bc\), \(ca\) がいずれも \(G\) に存在しないような \(G\) の頂点 \(a\), \(b\), \(c\) が存在する。
この命題は多重グラフでも成り立つ1。多重グラフ \(G\) を台単純グラフ \(G^{\operatorname*{simp}}\) に置き換えても命題の意味が変わらないためである。
3.3.2 次数
定義 2.4.1 では単純グラフ \(G=\left( V,E\right) \) の頂点 \(v\) の次数を次のように定義した:
この等式変形は \(G\) が多重グラフだと成り立たない。平行辺は同じ頂点を接続するので、多重グラフでは「\(v\) の隣接頂点の個数」が \(\deg v\) の下界にしかならない。
「\(n\) 個の頂点を持つ単純グラフ \(G\) では任意の頂点 \(v\) が \(\deg v\in\left\{ 0,1,\ldots,n-1\right\} \) を満たす」という命題 2.4.2 も多重グラフでは成り立たない。なぜなら、多重グラフには好きなだけ辺を加えることができ、それぞれの辺は端点の次数を \(1\) ずつ増加させるからである。
命題 2.4.3 は多重グラフでも成り立つだろうか? 次数の定義でループは二度数えると定めているので、この命題は成り立つ。ただ、証明には少し手直しが必要になる。これから以前に示したものと少し異なる証明を示す。まずは、命題 2.4.3 を多重グラフに対する命題に書き換える:
\(G\) を多重グラフとする。\(G\) の頂点の次数の和は \(G\) の辺の個数の二倍に等しい。言い換えれば、次の等式が成り立つ:
\(G=\left( V,E,\varphi\right) \) とする。このとき \(\operatorname*{V}\left( G\right) =V\) および \(\operatorname*{E}\left( G\right) =E\) である。
それぞれの辺 \(e\) に対して任意に選んだ端点を \(\alpha\left( e\right) \) と定め、もう一方の端点を \(\beta\left( e\right) \) と定める。\(e\) がループなら \(\beta\left( e\right) =\alpha\left( e\right) \) と定める。このとき、各頂点 \(v\) で次の等式が成り立つ:
この等式を全ての頂点 \(v \in V\) にわたって足し上げれば、次の等式を得る:
ここで、次の等式が成り立つ:
なぜなら、それぞれの辺 \(e \in E\) が和に \(1\) だけ寄与するからである。同様に次の等式も成り立つ:
以上で命題 3.3.2 は証明された。□
この命題が成り立つことは、ループを二度数えるものとして次数を定義する大きな動機の一つである。
握手補題 (系 2.4.4) は多重グラフでも成り立つ。つまり、次の命題が成り立つ:
\(G\) を多重グラフとする。\(G\) の頂点 \(v\) で次数 \(\deg v\) が奇数であるものは偶数個存在する。
単純グラフの場合と同様に命題 3.3.2 から従う。□
命題 2.4.5 は多重グラフでは成り立たない。例えば、多重グラフ  の三頂点はそれぞれ \(1\), \(2\), \(3\) の次数を持つ。幸い、命題 2.4.5 は有用だからというよりも興味深いから示した側面が大きい。
の三頂点はそれぞれ \(1\), \(2\), \(3\) の次数を持つ。幸い、命題 2.4.5 は有用だからというよりも興味深いから示した側面が大きい。
Mantel の定理 (定理 2.4.6) も多重グラフでは成り立たない。接続しても三角形が生じない二頂点 (あるいは既に接続している二頂点) の間に辺を追加し続ければいずれ \(e>n^{2}/4\) が満たされる。そのため、Turán の定理 (定理 2.4.8) も多重グラフでは成り立たない。
3.3.3 グラフ同型写像
グラフの同型性 (および同型写像) は多重グラフに対しても定義される。しかし、その定義は単純グラフのものと同じではない。多重グラフではグラフ同型写像を頂点集合間の全単射と定義することはできず、辺に対する処理が必要になる。具体的には、次のように定義される:
\(G=\left( V,E,\varphi\right) \) と \(H=\left( W,F,\psi\right) \) を二つの多重グラフとする。
-
\(G\) から \(H\) へのグラフ同型写像 (graph isomorphism) とは、次の条件を満たす全単射の組 \(\left( \alpha,\beta\right) \) である。まず、\(\alpha\) と \(\beta\) は次の定義域と値域を持つ:
\[ \begin{aligned} \alpha &\colon V\rightarrow W \\ \beta &\colon E\rightarrow F \end{aligned} \]次に、任意の \(e \in E\) に対して \(\beta\left( e\right) \) の端点は \(e\) の端点に対する \(\alpha\) の値域に等しい。この条件は可換図式を使って次のようにも表せる:
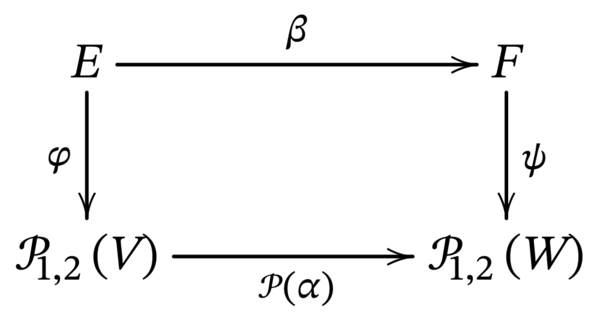
ここで \(\mathcal{P}\left( \alpha\right) \) は \(\mathcal{P}_{1,2}\left( V\right) \) から \(\mathcal{P}_{1,2}\left( W\right) \) への写像であり、\(V\) の部分集合 \(\left\{ u,v\right\} \in\mathcal{P}_{1,2}\left( V\right) \) を \(\left\{ \alpha\left( u\right) ,\alpha\left( v\right) \right\} \in\mathcal{P}_{1,2}\left( W\right) \) に移す。 グラフ同型写像は単に同型写像 (isomorphism) とも呼ぶ。
-
\(G\) から \(H\) へのグラフ同型写像が存在するとき、\(G\) と \(H\) は同型 (isomorphic) であると言い、\(G\cong H\) と書く。
多重グラフの同型関係も同値関係となる。
3.3.4 完全グラフ・路・閉路
定義 2.6.1、定義 2.6.2、定義 2.6.3 では完全グラフ \(K_{n}\), 路グラフ \(P_{n}\), 閉路グラフ \(C_{n}\) を単純グラフとしてそれぞれ定義した。もちろん、これらのグラフは必要に応じて多重グラフとみなすことができる。
ただ、多重グラフを考えるときは \(n\) 次の閉路グラフ \(C_{n}\) の定義を \(n=1\) のときにも拡張できる。また、多重グラフにおける \(C_{2}\) の自然な定義は単純グラフにおける \(C_{2}\) の定義と異なる。そのため次のように定める:
閉路グラフの定義 (定義 2.6.3) を次のように変更する。
この定義があると、全ての \(n \geq 1\) に対して \(n\) 次の閉路グラフ \(C_{n}\) が \(n\) 個の辺を持つようになる。単純グラフでは \(n=2\) のときだけ \(C_{n}\) の辺の個数が \(1\) だった。
3.3.5 誘導部分多重グラフ
定義 2.7.1 では、単純グラフの部分グラフと誘導部分グラフを定義した。多重グラフに対する同様の概念は次のように定義される:
\(G=\left( V,E,\varphi\right) \) を多重グラフとする。
-
\(W \subseteq V\) かつ \(F\subseteq E\) かつ \(\psi=\varphi|_{F}\) を満たす多重グラフ \(H=\left( W,F,\psi\right) \) を \(G\) の部分多重グラフ (submultigraph) と呼ぶ。言い換えれば、\(G\) の部分多重グラフは頂点が \(G\) の頂点で、辺が \(G\) の辺で、辺の端点が \(G\) が持つ同じ辺の端点と等しい。
部分多重グラフを単に部分グラフ (subgraph) と呼ぶこともある。
-
\(S\) を \(V\) の部分集合とする。集合 \(S\) に関する \(G\) の誘導部分多重グラフ (induced submultigraph of \(G\) on the set \(S\)) とは、次に示す \(G\) の部分多重グラフを言う:
\[ \left( S,\ \ E^{\prime},\ \ \varphi|_{E^{\prime}}\right) \]ここで \(E^{\prime}\) は次のように定義される:
\[ E^{\prime}\colonequals \left\{ e\in E\mid e \text{ の端点が全て } S \text{ に属する}\right\} \]言い換えれば、これは \(G\) の多重部分グラフであり、\(S\) を頂点集合として持ち、端点が両方とも \(S\) に含まれる \(G\) の辺全体からなる集合を辺集合として持つ。この誘導部分多重グラフを \(G\left[ S\right] \) と表記する。
-
\(G\) の誘導部分多重グラフ (induced submultigraph) とは、何らかの \(S\subseteq V\) に関する \(G\) の誘導部分多重グラフを意味する。
接中辞の「多重」を省略する場合も多い。つまり「部分多重グラフ」は単に「部分グラフ」とも呼ばれる。
以上の定義があると、多重グラフが持つ閉路は閉路グラフと同型な部分グラフと同じだと言える: 多重グラフ \(G\) に含まれる長さ \(n\) の閉路は、\(C_{n}\) と同型な \(G\) の部分多重グラフと同じである。証明は読者に任せる。
3.3.6 非交和
第 2.8 節では、二つ以上の単純グラフの非交和を定義した。多重グラフの非交和は簡単に定義できるので、読者に任せる。
3.3.7 歩道
多重グラフにおける歩道・路・閉歩道・閉路は第 3.1 節で定義した。歩道の長さ (length) は単純グラフの場合と同様に歩道に含まれる辺の個数として定義される。第 2.9 節で見た基礎的な性質が多重グラフで成り立つかどうかを見ていこう。
まず、路の辺は必ず相異なる。これは単純グラフの場合と同じく簡単に証明できる。
次に、多重グラフでも二つの歩道を「連結」できるかどうかを考えよう:
\(G\) を多重グラフ、\(u\), \(v\), \(w\) を \(G\) の三頂点、\(\mathbf{a}=\left( a_{0},e_{1},a_{1},\ldots ,e_{k},a_{k}\right) \) を \(u\) から \(v\) への歩道、\(\mathbf{b}=\left( b_{0},f_{1},b_{1},\ldots,f_{\ell},b_{\ell}\right) \) を \(v\) から \(w\) への歩道とする。このとき
は \(u\) から \(w\) への歩道である。この歩道を今後 \(\mathbf{a}\ast\mathbf{b}\) と表記する。
歩道は「逆走」することで反転できる:
\(G\) を多重グラフ、\(u\), \(v\) を \(G\) の二頂点、\(\mathbf{a}=\left( a_{0},e_{1},a_{1},\ldots,e_{k},a_{k}\right) \) を \(u\) から \(v\) への歩道とする。このとき:
-
\(\mathbf{a}\) の要素を逆順に並べた列 \(\left( a_{k},e_{k},a_{k-1},e_{k-1},\ldots ,e_{1},a_{0}\right) \) は \(v\) から \(u\) への歩道である。この歩道を \(\mathbf{a}\) の反転 (reversal) と呼び、\(\operatorname*{rev}\mathbf{a}\) と表記する。
-
\(\mathbf{a}\) が路なら、\(\operatorname*{rev}\mathbf{a}\) も路となる。
歩道が路でないなら、同じ頂点間のそれより短い歩道が存在する:
\(G\) を多重グラフ、\(u\), \(v\) を \(G\) の二頂点、\(\mathbf{a}=\left( a_{0},e_{1},a_{1},\ldots,e_{k},a_{k}\right) \) を \(u\) から \(v\) への歩道とする。\(\mathbf{a}\) が路でないなら、長さが \(k\) より小さい \(u\) から \(v\) への歩道が存在する。
\(G\) を多重グラフ、\(u\), \(v\) を \(G\) の二頂点とする。\(u\) から \(v\) への長さ \(k \in \mathbb{N}\) の歩道が存在するなら、長さが \(k\) 以下の \(u\) から \(v\) への路が存在する。
これらの結果は単純グラフに対する同様の結果と同じように証明できる。歩道に辺を記録する必要がある点が唯一異なる。
第 2.9.4 項で単純グラフに対して考えた五つの問題は、多重グラフ \(G\) に対しても考えられる。以前に示した解答を多重グラフに対して適用する上で必要になる根本的な変更は存在しない。唯一、路または閉路が利用する辺を記録しなければならない点に関して変更が必要になる。
3.3.8 路連結性
多重グラフの二頂点間の路連結性という関係は単純グラフの二頂点間の路連結性 (定義 2.9.8) と同様に定義され、同じ記号 \(\simeq_{G}\) で表記される。多重グラフを考えているときでも \(\simeq_{G}\) は同値関係である (証明は単純グラフの場合と同様)。また、次の命題も単純グラフの場合と同様の証明で示せる:
\(G\) を多重グラフ、\(u\), \(v\) を \(G\) の二頂点とする。このとき \(u\) から \(v\) への路が存在するとき、かつそのときに限って \(u\simeq_{G}v\) が成り立つ。
多重グラフに対する成分 (component) と連結 (connected) の定義は単純グラフに対する定義 (定義 2.9.11 と定義 2.9.12) と同じである。次の命題は、以前に単純グラフに対する同様の命題を示したのと同じ方法で示せる:
\(G\) を多重グラフ、\(C\) を \(G\) の成分とする。
このとき \(C\) に関する \(G\) の誘導部分多重グラフは連結である。
\(G\) を多重グラフ、\(C_{1},C_{2},\ldots,C_{k}\) を \(G\) の全ての成分とする (\(C_{1},C_{2},\ldots,C_{k}\) に重複はないとする)。
このとき \(G\) は非交和 \(G\left[ C_{1}\right] \sqcup G\left[ C_{2}\right] \sqcup\cdots\sqcup G\left[ C_{k}\right] \) と同型である。
次の命題は命題 2.10.4 に対応する:
\(G\) を多重グラフとする。\(G\) の歩道 \(\mathbf{w}\) が「任意の隣接する辺が同一でない」という条件を満たすとする。
このとき \(\mathbf{w}\) は路であるか、そうでなければ閉路を含む (\(\mathbf{w}\) の辺からなる \(G\) の閉路が存在する)。
この命題の証明は単純グラフに対する同様の命題 (命題 2.10.4) の証明と似ている部分がある。ただ、歩道 \(\left( w_{i},w_{i+1},\ldots,w_{j}\right) \) が閉路だと示す部分に少し変更が必要になる。当然、閉路だと示す歩道は \(\left( w_{i},w_{i+1},\ldots,w_{j}\right) \) ではなく辺を含んだ \(\left( w_{i},e_{i+1},w_{i+1},\ldots,e_{j},w_{j}\right) \) である2。□
単純グラフの場合と同様に、この命題からは次の系が得られる:
\(G\) を多重グラフ、\(\mathbf{w}\) を \(G\) の閉歩道とする。\(\mathbf{w}\) の長さが \(0\) より大きく、\(\mathbf{w}\) で隣り合う任意の二辺が相異なるとき、\(G\) は閉路を持つ。
定理 2.10.7 と同様の定理も成り立つ:
\(G\) を多重グラフ、\(u\) と \(v\) を \(G\) の二頂点とする。\(u\) から \(v\) への異なる路が二つあるなら、\(G\) は閉路を持つ。
定理 2.10.7 の証明に自明な変更を加えれば、この定理に対する証明となる (具体的には、辺 \(p_{a-1}p_{a}\), \(q_{b-1}q_{b}\) ではなく歩道 \(\mathbf{p}\), \(\mathbf{q}\) の最後の辺を使って議論する必要がある)。□
一方、多重グラフでは命題 2.11.1 は成り立たない。実際、多重グラフでは任意の頂点にループを好きなだけ付けることができるので、長さが \(1\) より大きい閉路を作らずに頂点の次数をいくらでも増やせる。
3.3.9 辺の除去、橋、切断辺
続いて \(G \setminus e\) の定義 (定義 2.12.1) を多重グラフに拡張する:
\(G=\left( V,E,\varphi\right) \) を多重グラフ、\(e\) を \(G\) の辺とする。このとき \(G\) から辺 \(e\) を除去して得られる多重グラフを \(G \setminus e\) と表記する。言い換えれば、\(G \setminus e\) を次のように定める:
\(G\setminus e\) を \(G-e\) と書く文献もある。
定理 2.12.2 と同様の命題は多重グラフでも成り立つ。証明も定理 2.12.2 と同様にできる:
\(G\) を多重グラフ、\(e\) を \(G\) の辺とする。このとき:
-
\(e\) を含む \(G\) の閉路が存在するなら、\(G\setminus e\) の成分は \(G\) の成分と等しい。
-
\(e\) を含む \(G\) の閉路が存在しないなら、\(G\setminus e\) は \(G\) より一つだけ多い成分を持つ。
辺 \(e\) がループである場合、\(e\) を含む閉路 (辺として \(e\) だけを含む長さ \(1\) の閉路) が必ず存在し、\(e\) を含む路は存在しないことに注意してほしい。そのため、ループである辺を取り除いても路連結性という関係は変化しない。
多重グラフにおける橋と切断辺は単純グラフにおける定義 (定義 1.12.4) と同様に定義される。次の系も同様に成り立つ:
\(G\) を多重グラフ、\(e\) を \(G\) の辺とする。\(e\) は橋であるとき、かつそのときに限って切断辺となる。
系 2.12.5 と同じように示せる。□
3.3.10 支配集合
支配集合の定義と性質は第 2.13 節で見た。多重グラフにおける支配集合は単純グラフの場合と同様に定義できるものの、そこから興味深い結果は得られない。実は、多重グラフ \(G\) の支配集合は単純グラフ \(G^{\operatorname*{simp}}\) の支配集合と一致する。そのため、多重グラフの支配集合に関する任意の命題は単純グラフの支配集合に関する命題に帰着できる。
3.3.11 ハミルトン路とハミルトン閉路
命題 3.2.5 から容易に分かるように、多重グラフ \(G\) は対応単純グラフ \(G^{\operatorname*{simp}}\) がハミルトン (閉) 路を持つとき、かつそのときに限ってハミルトン (閉) 路を持つ。しかし、これは単純グラフとハミルトン路に関して示してきた命題が多重グラフでも成り立つことを意味しない。例えば、Ore の定理 (定理 2.14.4) と Dirac の定理 (系 2.14.5) はどちらも多重グラフでは成り立たない。ハミルトン閉路を生じさせないように辺を好きなだけ増やせるためである。
命題 2.14.6 は多重グラフでも成り立つ。\(G^{\operatorname*{simp}}\) の性質から容易に証明できる。
3.3.12 練習問題
少なくとも一つの辺を持つ多重グラフを \(G\) とする。\(G\) の各頂点の次数が偶数なら \(G\) は閉路を持つと示せ。
\(G\) を多重グラフ、\(d > 2\) を整数とする。\(G\) の全ての頂点 \(v\) で \(\deg v > 2\) が成り立つとき、\(d\) で割り切れない長さを持つ閉路が \(G\) に存在することを示せ。
\(G\) を多重グラフとする。奇数の次数を持つ \(G\) の頂点がちょうど二つ存在するとき、その二つの頂点は路連結だと示せ。
ループを持たない多重グラフを \(G=\left( V,E,\varphi\right) \) とする。
辺 \(e \in E\) と \(e\) に含まれる頂点 \(v \in V\) に対して、\(e/v\) で \(v\) でない \(e\) の端点を表す。\(e\) がループなら、\(e/v\) は \(v\) を表す。
それぞれの \(v \in V\) に対して、有理数 \(q_{v}\) を次のように定義する:
次の不等式を示せ:
\(F\) を任意の体とする。
\(G = \left( V, E, \varphi\right) \) を多重グラフとする。ここで \(V = \left\{ 1, 2, \ldots, n \right\} \) (\(n \in \mathbb{N}\)) である。
各辺 \(e \in E\) に対して、ベクトル \(\chi_{e} \in F^{n}\) (\(n\) 個の要素からなる列ベクトル) を次のように構築する:
-
\(e\) がループなら、零ベクトルを \(\chi_{e}\) とする。
-
そうでないなら、\(e\) の端点を \(u\), \(v\) として、第 \(u\) 要素に \(1\) を、第 \(v\) 要素に \(-1\) を、それ以外の場所に \(0\) を持つ列ベクトルを \(\chi_{e}\) とする。
全ての \(e\in E\) に対する列ベクトル \(\chi_{e}\) を横に並べた \(F\) 上の \(n\times\left\vert E\right\vert \) 行列を \(M\) とする (列ベクトルを並べる順番は適当で構わない: 命題の真偽には影響しない)。\(G\) の成分の個数を \(\operatorname{conn} G\) と表すとき、次の等式を示せ:
[例: 次の多重グラフを \(G\) とする:
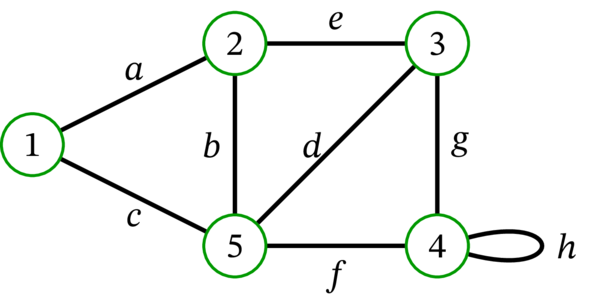
このとき \(n=5\) である。辺 \(b\) の端点に対して \(u = 2\), \(v = 5\) としたなら、\(\chi_{b}\) は次のようになる:
同じ辺で \(u = 5\), \(v=2\) としたなら、\(\chi_{b}\) は次のようになる:
\(\chi_{b}\) としてどちらを採用しても構わない。同様の列ベクトルを \(G\) の全ての辺に対して構築し、それらを横に並べれば \(M\) が得られる:
ここでは \(\chi_{a}\), \(\chi_{b}\), \(\chi_{c}\), \(\chi_{d}\), \(\chi_{e}\), \(\chi_{f}\), \(\chi_{g}\), \(\chi_{h}\) の順に列ベクトルを並べている。容易に分かるように \(\operatorname*{rank}M=4\) であり、これは \(\left\vert V\right\vert -\operatorname*{conn}G\) に等しい。]
[Remark: この練習問題で証明する命題は「全ての \(e \in E\) に対するベクトル \(\chi_{e}\) が張る空間は \(\left\vert V\right\vert -\operatorname*{conn}G\) の次元を持つ」と言い換えられる。
トポロジーの研究者は行列 \(M\) を「境界演算子 \(\partial\colon C_{1}\left( G\right) \rightarrow C_{0}\left( G\right) \) を表す行列」と捉えるだろう。このとき \(G\) は CW 複体 (CW-complex) となる。]
多重グラフ \(G\) に対して、\(G\) の成分の個数を \(\operatorname{conn} G\) と表す。
\(\left( V,H,\varphi\right) \) を多重グラフ、\(E\), \(F\) を \(H\) の部分集合とする。
-
次の不等式を示せ:
\[ \begin{aligned} & \operatorname{conn}\left( V,\ E,\ \varphi|_{E}\right) +\operatorname{conn}\left( V,\ F,\ \varphi|_{F}\right) \nonumber\\ & \quad \leq\operatorname{conn}\left( V,\ E\cup F,\ \varphi|_{E\cup F}\right) +\operatorname{conn}\left( V,\ E\cap F,\ \varphi|_{E\cap F}\right) \end{aligned} \][ヒント: 単純グラフの場合を考えても構わない。つまり、単純グラフ \(G = \left(V, E\right)\) と \(V\) の部分集合 \(E\), \(F\) に対する次の不等式の証明を解答としてよい:
\[ \begin{aligned} & \operatorname{conn}\left( V,\ E\right) +\operatorname{conn}\left( V,\ F\right) \\ &\quad \leq\operatorname{conn}\left( V,\ E\cup F\right) +\operatorname{conn}\left( V,\ E\cap F\right) \end{aligned} \]こうしたとしても多重グラフの場合と比べて問題が本質的に簡単になるわけではない。ただ、写像 \(\varphi\) を考える必要がなくなる。]
-
前問の不等式が等式とならない例を示せ。
\(2m\) 個の辺を持つ連結な多重グラフを \(G=\left( V,E,\varphi\right) \) とする (\(m \in \mathbb{N}\))。二つの異なる辺からなる集合 \(\left\{ e,f\right\} \) が友好組 (friendly couple) とは、\(e\) と \(f\) が共通の端点を少なくとも一つ持つことを言う。共通要素を持たない \(m\) 個の友好組に \(G\) の辺集合を分解できると示せ。言い換えれば、共通要素を持たない \(m\) 個の友好組 \(\left\{ e_{1},f_{1}\right\}\), \(\left\{ e_{2},f_{2}\right\}\), ..., \(\left\{ e_{m},f_{m}\right\} \) であって \(E=\left\{ e_{1},f_{1},e_{2},f_{2},\ldots,e_{m},f_{m}\right\} \) を満たすものが存在することを示せ。
[例: 偶数個の辺を持つ多重グラフの例を示す:
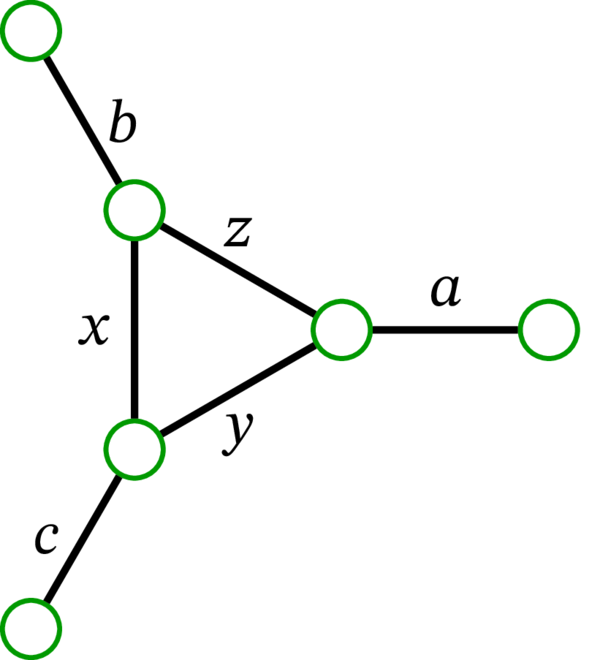
このグラフでは \(\left\{a,z\right\}\), \(\left\{b,x\right\}\), \(\left\{c,y\right\}\) が条件を満たす友好組の例である。]
\(n \geq 0\) を整数、和 \(d_{1}+d_{2}+\cdots+d_{n}\) が偶数となるような \(n\) 個の非負整数を \(d_{1},d_{2},\ldots,d_{n}\) とする。
-
頂点集合が \(\left\{ 1,2,\ldots,n\right\} \) で、全ての \(i\in\left\{ 1,2,\ldots ,n\right\} \) が \(\deg i=d_{i}\) を満たす多重グラフ \(G\) が存在することを示せ。
-
頂点集合が \(\left\{ 1,2,\ldots,n\right\} \) で、全ての \(i\in\left\{ 1,2,\ldots ,n\right\} \) が \(\deg i=d_{i}\) を満たすループを持たない多重グラフ \(G\) が存在するのは、全ての \(i\in\left\{ 1,2,\ldots,n\right\} \) が次の不等式を満たすとき、かつそのときに限ると示せ:
\[ \begin{aligned} \sum_{\substack{j\in\left\{ 1,2,\ldots,n\right\} ;\\j\neq i}}d_{j}\geq d_{i} \end{aligned} \]
ループを持たない多重グラフを \(G\) とする。辺が相異なる \(G\) の歩道を \(G\) の小道 (trail) と呼ぶ (小道の頂点は重複しても構わない)。\(u\), \(v\) を \(G\) の二頂点とする。歩道と同様に、「\(u\) から \(v\) への小道」とは「\(u\) で始まって \(v\) で終わる小道」を意味する。次の等式を示せ:
全ての頂点が偶数の次数を持つ多重グラフを \(G\)、\(u\), \(v\) を \(G\) の異なる二頂点とするとき、\(u\) から \(v\) への路の個数は偶数だと示せ。
\(G=\left( V,E,\varphi\right) \) を \(\left\vert E\right\vert >\left\vert V\right\vert \) が成り立つ多重グラフ、\(n=\left\vert V\right\vert \) とする。長さが \(\dfrac{2n+2}{3}\) 以上の閉路を \(G\) が持つことを示せ。
-
もちろん、用語を適切に読み替える必要はある: 例えば「辺 \(ab\) が存在する」は「\(a\) と \(b\) を端点に持つ辺が存在する」と読み替える。 ↩︎
-
大まかな証明の流れを次に示す:
\(\mathbf{w} = \left( w_{0},e_{1},w_{1},e_{2},w_{2},\ldots,w_{k},e_{k}\right)\) が路でないと仮定する。このとき \(i < j\) かつ \(w_{i}=w_{j}\) を満たす整数の組 \(\left( i,j\right) \) が存在する。そのような組の中で差 \(j-i\) が最小のものを選ぶ。このとき \(\left( w_{i},e_{i+1},w_{i+1},\ldots,e_{j},w_{j}\right) \) は閉歩道である。これから、この閉歩道が閉路だと示す。そのためには、次の三点を示す必要がある:
-
頂点 \(w_{i},w_{i+1},\ldots,w_{j-1}\) が相異なる
-
辺 \(e_{i+1},e_{i+2},\ldots,e_{j}\) が相異なる。
-
\(j-i\geq1\) が成り立つ。
一つ目の命題は \(j-i\) の最小性、三つ目の問題は \(i < j\) から示せる。後は二つ目の命題を示せばよい。「\(e_{i+1},e_{i+2},\ldots,e_{j}\) が相異なる」を言い換えた「\(i < a < b\leq j\) を満たす任意の \(a\), \(b\) に対して \(e_{a}\neq e_{b}\)」をこれから示す。\(a=b-1\) の場合と \(a \neq b-1\) の場合を分けて考える。
もし \(a=b-1\) なら \(e_{a}\) と \(e_{b}\) は \(\mathbf{w}\) で隣り合う辺なので、問題の仮定より相異なる。これで \(a=b-1\) の場合は証明できた。
続いて \(a \neq b-1\) の場合を考える。\(a \neq b-1\) と \(a < b\) より \(a < b - 1\) が分かり、\(i < a\) より \(i \leq a-1\) が分かる。これらと \(b \leq i\) から \(i\leq a-1 < a < b-1\leq j-1\) を得る。よって \(b-1\), \(a-1\), \(a\) は \(\left\{ i,i+1,\ldots ,j-1\right\} \) の異なる三要素である。頂点 \(w_{i},w_{i+1},\ldots,w_{j-1}\) は相異なるので、ここから \(w_{b-1},w_{a-1},w_{a}\) は相異なると分かる。ここから \(w_{b-1}\notin\left\{ w_{a-1},w_{a}\right\} =\varphi\left( e_{a}\right) \) を得る。一方 \(\mathbf{w}\) は歩道より \(e_{b}\) の端点は \(w_{b-1}\) と \(w_{b}\) であり、\(\varphi\left( e_{b}\right) =\left\{ w_{b-1},w_{b}\right\} \) が成り立つ。\(w_{b-1}\in\left\{ w_{b-1},w_{b}\right\} =\varphi\left( e_{b}\right) \) と \(w_{b-1}\notin\varphi\left( e_{a}\right) \) から、集合 \(\varphi\left( e_{b}\right) \) と \(\varphi\left( e_{a}\right) \) が等しくないこと分かる。言い換えれば \(\varphi\left( e_{b}\right) \neq\varphi\left( e_{a}\right) \) である。したがって \(e_{a}\neq e_{b}\) であり、\(a\neq b\) の場合も証明できた。
両方の場合で \(e_{a}\neq e_{b}\) だと示せたので、証明は完了した。 ↩︎
-