2.12. グラフの橋

後に重要となる質問がひとつある: グラフから辺を一つ除去すると、何が起こるだろうか？ この操作を表す記法をまずは定義しよう:

\(G\setminus e\) を \(G-e\) と表記する文献もある。

例 2.12.3

次の図が表すグラフを \(G\) とする:

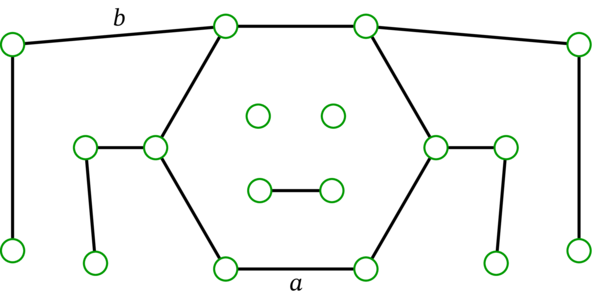
[\(a\) と \(b\) は後の議論で参照できるように辺に付けたラベルである。] このグラフは \(4\) 個の成分を持つ。辺 \(a\) を含む \(G\) の閉路は存在し、辺 \(b\) を含む閉路は存在しない。定理 2.12.2 (a) で \(e =a\) とすれば、\(G \setminus a\) の成分は \(G\) の成分と一致することが分かる。\(G \setminus a\) の描画を次に示す:

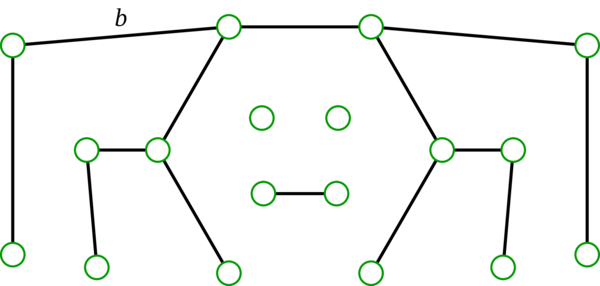
このグラフが \(4\) 個の成分を持つことは視覚的に分かる。一方、定理 2.12.2 (b) で \(e = b\) とすれば、\(G \setminus b\) は \(G\) より一つ多い成分を持つことが分かる。\(G \setminus b\) の描画を次に示す:

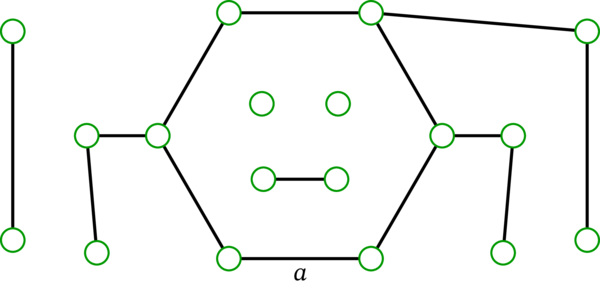
このグラフが \(5\) 個の成分を持つことは視覚的に分かる。

[定理 2.12.2 の証明] 証明の流れだけを説明する。詳細は [21f6, § 6.7] を参照してほしい。

\(u\) と \(v\) を \(e\) の端点とする (つまり \(e = uv\) とする)。\(\left( u,v\right) \) は \(G\) の辺なので、\(u\simeq_{G}v\) が成り立つ。

(a): \(e\) を含む閉路が \(G\) に存在すると仮定する。このとき、もし \(e\) を閉路から取り除いたとしても、\(u\) から \(v\) への路はグラフに残る (閉路の残りの辺が「迂回路」となる)。この路は \(G \setminus e\) における路でもあるので、\(u\simeq_{G\setminus e}v\) を得る。

続いて、\(G\setminus e\) の成分が \(G\) の成分と一致することを示す必要がある。これは関係 \(\simeq_{G\setminus e}\) と関係 \(\simeq_{G}\) が等価だと示せれば直ちに従う (グラフの成分は路連結性という関係の同値類と定義されるため)。これから関係 \(\simeq_{G\setminus e}\) と関係 \(\simeq_{G}\) が等価なことを示す。

\(G\) の任意の二頂点 \(x\), \(y\) に対して、\(x \simeq_{G} y\) が成り立つのは \(x \simeq_{G\setminus e} y\) が成り立つとき、かつそのときに限ることを証明したい。「そのときに限る」の方向は明らかである: \(G \setminus e\) における歩道は必ず \(G\) における歩道でもある。よって後は「成り立つとき」の方向を示せばよい。つまり \(G\) の二頂点 \(x\), \(y\) が \(x\simeq_{G}y\) を満たすとき \(x\simeq_{G\setminus e}y\) だと示す必要がある。

\(x\simeq_{G}y\) と命題 2.9.10 より、\(G\) における \(x\) から \(y\) への路 \(\mathbf{w}\) が存在する。\(\mathbf{w}\) が \(e\) を使わない¹なら、\(\mathbf{w}\) は \(G \setminus e\) における路でもあるので、\(x\simeq_{G\setminus e}y\) が分かって証明が完了する。続いて、\(\mathbf{w}\) が \(e\) を使う場合を考える。このとき \(e\) の端点 \(u\), \(v\) が \(\mathbf{w}\) に含まれる。一般性を失うことなく、\(\mathbf{w}\) において \(u\) が \(v\) より早く現れると仮定できる (もしそうでないなら、\(u\) と \(v\) の名前を交換する)。\(\mathbf{w}\) は次の形をしている:

辺 \(e=uv\) を除去すると、\(\mathbf{w}\) は次の二つの部分に分かれる:

[路の辺は相異なるので、\(e\) は \(\mathbf{w}\) に一度しか現れない。] この二つの路はいずれも \(G \setminus e\) の路なので、\(x\simeq _{G\setminus e}u\) と \(v\simeq_{G\setminus e}y\) が分かる。\(\simeq_{G\setminus e}\) が同値関係であることを思い出せば、次を得る:

よって \(x\simeq_{G\setminus e}y\) であり、定理 2.12.2 (a) は証明された。

(b): \(e=uv\) を含む閉路が \(G\) に存在しないと仮定する。\(G \setminus e\) が \(G\) より一つだけ多い成分を持つことを証明する必要がある。これは次の二つの命題を示せば証明される:

Claim 2 は簡単に分かる: \(u\) と \(v\) を含まない \(G\) の成分は (\(e\) の端点を含まないので) \(e\) を除去しても変化しない。つまり、そういった成分は \(G\setminus e\) の成分でもある。 [「この部分を数学的に正確な議論に書き換えよ」は良い練習問題である。[21f6, § 6.7] に解答例がある。]

後は Claim 1 を示せばよい。そのために新しい記号を定義する:

• \(u\) と \(v\) を含む \(G\) の成分を \(C\) とする。

• \(u\) を含む \(G \setminus e\) の成分を \(A\) とする。

• \(v\) を含む \(G \setminus e\) の成分を \(B\) とする。

示すべきは \(A\cup B=C\) と \(A\cap B=\varnothing\) である。

\(A\cap B=\varnothing\) を示すには、\(u\simeq_{G\setminus e}v\) が成り立たないことを示せればよい (\(A\) と \(B\) はそれぞれ \(u\) と \(v\) の関係 \(\simeq_{G\setminus e}\) に関する同値類であるため)。背理法でこれを示す。\(u\simeq_{G\setminus e}v\) と仮定する。このとき \(u\) から \(v\) への路が \(G \setminus e\) に存在する。\(e=uv\) だから、この路の最後に \(e\) を追加すると路を「閉じる」ことができる: このとき \(e\) を含む \(G\) における閉路が得られる。しかし、これは \(e\) を含む閉路が \(G\) に存在しない仮定と矛盾する。矛盾が得られたので仮定は間違いであり、\(u\simeq_{G\setminus e}v\) は成り立たないと分かる。よって上述したように \(A\cap B=\varnothing\) である。

続いて \(A\cup B=C\) を示す。\(A\) と \(B\) は明らかに [\(G\setminus e\) における歩道は \(G\) における歩道でもあるので、\(G\setminus e\) の任意の成分は \(G\) の何らかの成分の部分集合であるために] \(C\) の部分集合なので、\(A\cup B\subseteq C\) が分かる。よって後は \(C \subseteq A\cup B\) を示せばよい。これから任意の \(c \in C\) が \(A \cup B\) に属することを示す。

頂点 \(c\in C\) を取る。\(C\) は \(u\) が属する \(G\) の成分なので、このとき \(c\simeq_{G}u\) が成り立つ。よって \(G\) には \(c\) から \(u\) への路 \(\mathbf{p}\) が存在する。以降の議論は二つの場合に分かれる:

• Case 1: この路 \(\mathbf{p}\) が辺 \(e\) を使わない。この場合、\(\mathbf{p}\) は \(G \setminus e\) における路でもあるので、\(c\simeq_{G\setminus e}u\) が分かる。\(u\) が属する \(G\setminus e\) の成分が \(A\) だったから、\(c\in A\) が分かる。

• Case 2: この路 \(\mathbf{p}\) が辺 \(e\) を使う。この場合、\(e\) は \(\mathbf{p}\) の最後の辺でなければならない (そうでなければ \(\mathbf{p}\) は \(u\) を二度含むことになる²ものの、路は一つの頂点を一度しか通れない)。従って \(\mathbf{p}\) の最後から二番目の頂点は \(v\) で、最後の頂点は \(u\) である。よって \(\mathbf{p}\) から最後の頂点を除去すれば、\(c\) から \(v\) への路が得られる。こうして得られる路は (\(u\) を含まず、従って \(e\) を使わないので) \(G \setminus e\) における路でもある。つまり \(c\simeq_{G\setminus e}v\) が分かる。\(v\) の属する \(G \setminus e\) の成分が \(B\) だったから、\(c\simeq_{G\setminus e}v\) を言い換えれば \(c \in B\) である。

いずれの場合でも \(c\) は \(A\) または \(B\) に属する。つまり \(c \in A \cup B\) である。これが示したかったことであり、以上で定理 2.12.2 (b) は証明された。□

続いて、グラフ理論で広く使われる用語を定義する:

[証明] 定理 2.12.2 から従う。□

切断頂点も定義できる: 単純グラフ \(G\) の頂点 \(v\) は、\(G\setminus v\) (\(G\) から頂点 \(v\) を除去³したグラフ) が \(G\) より多い成分を持つとき、切断頂点 (cut-vertex) と呼ばれる。ただし残念ながら、系 2.12.5 の切断頂点バージョンと呼べる命題は存在しない。また、頂点の除去による成分の増加は (辺の除去と異なり) \(1\) より大きくなる場合がある (さらに、除去する頂点の次数が \(0\) の場合は成分の個数が減る)。例えば、次のグラフから頂点 \(0\) を除去したグラフを考えてみてほしい:

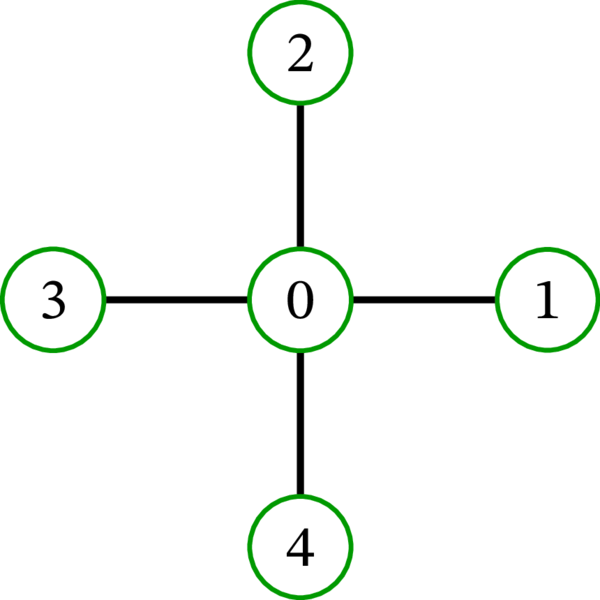
そのグラフは集合 \(\left\{ 1,2,3,4\right\} \) 上の空グラフであり、頂点 \(0\) の除去によって成分の個数は \(1\) から \(4\) に増加する。