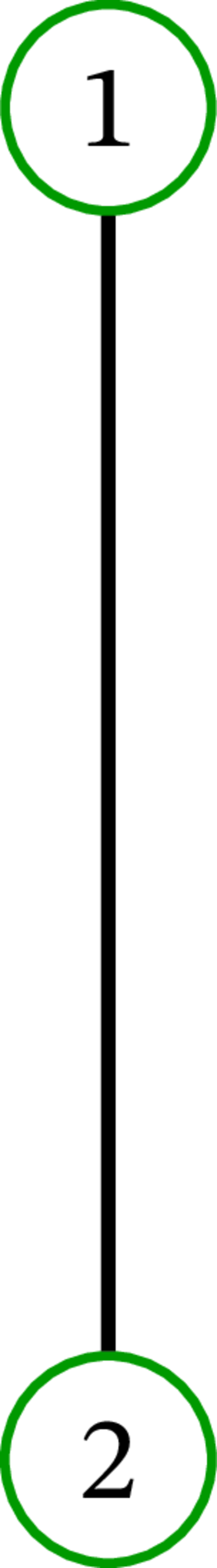2.6. 特別なグラフ

本節では特に重要なグラフの族をいくつか定義する。

2.6.1完全グラフと空グラフ

最も簡単なグラフの族は、完全グラフと空グラフである:

定義 2.6.1

\(V\) を有限集合とする。

単純グラフ \(\left( V,\ \mathcal{P}_{2}\left( V\right) \right) \) を \(V\) 上の完全グラフ (complete graph on \(V\)) と呼ぶ。これは頂点集合が \(V\) で、任意の相異なる二頂点が隣接する単純グラフである。

ある \(n\in\mathbb{N}\) で \(V=\left\{ 1,2,\ldots,n\right\} \) が成り立つとき、この \(V\) 上の完全グラフを \(K_{n}\) と表記する。
単純グラフ \(\left( V,\ \varnothing\right) \) を \(V\) 上の空グラフ (empty graph on \(V\)) と呼ぶ。これは頂点集合が \(V\) で辺を持たないグラフである。

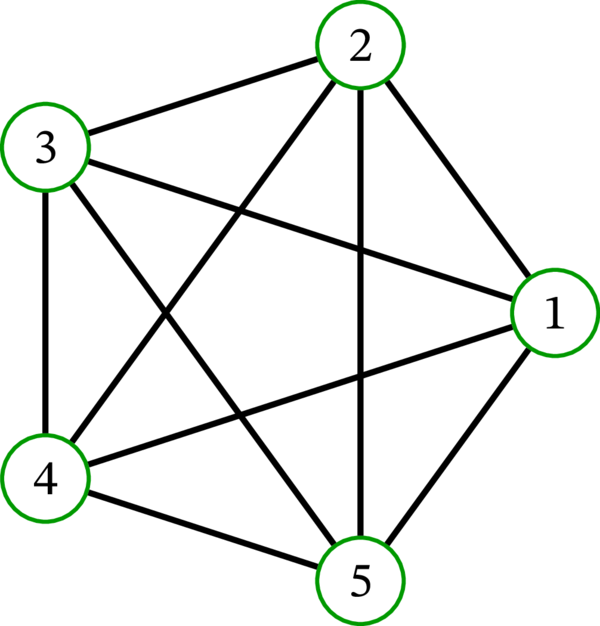
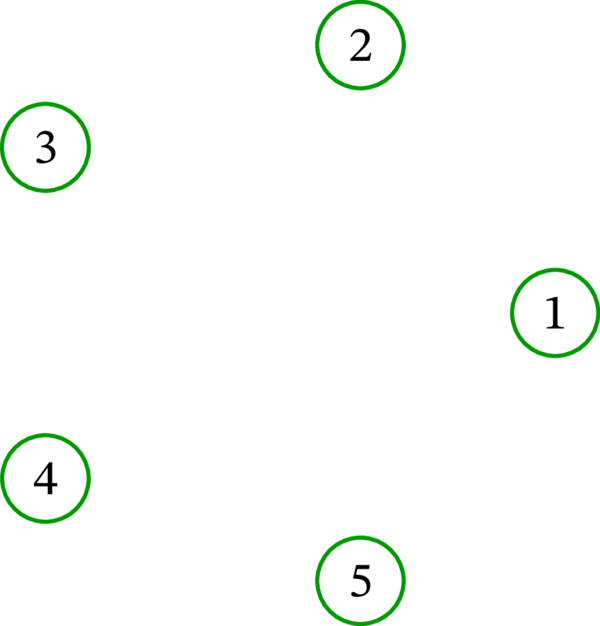
集合 \(\left\{ 1,2,3,4,5\right\} \) 上の完全グラフと空グラフを次の図に示す:

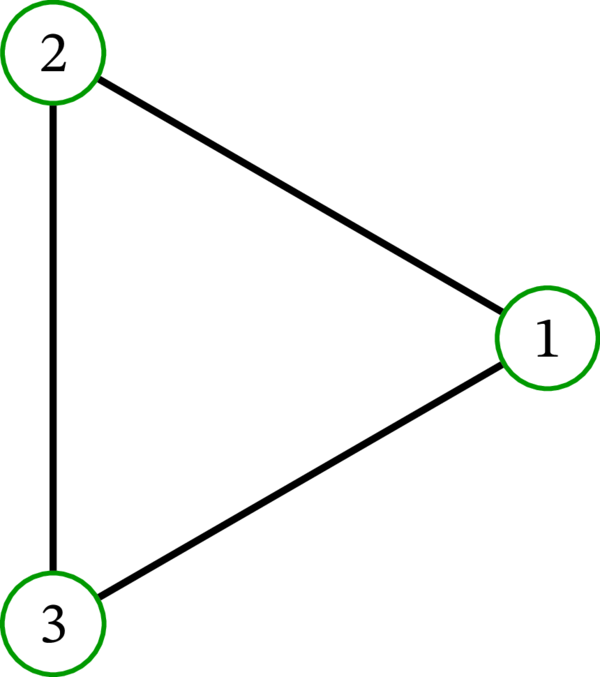
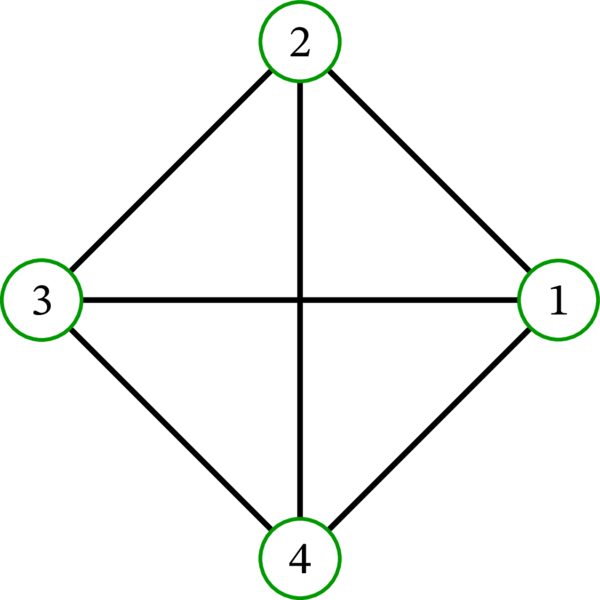
左のグラフは \(K_{5}\) と表記される。

完全グラフ \(K_{0},K_{1},K_{2},K_{3},K_{4}\) を次に示す:

なお、単純グラフ \(G\) が完全グラフ \(K_n\) と同型となるのは \(G\) が \(n\) 頂点を持つ完全グラフ (相異なる二頂点が全て隣接するグラフ) であるとき、かつそのときに限る。

質問: 二つの有限集合 \(V\), \(W\) が与えられたとき、\(V\) 上の完全グラフから \(W\) 上の完全グラフへの同型写像は何か？

解答: \(\left\vert V\right\vert \neq\left\vert W\right\vert \) なら同型写像は存在しない。\(\left\vert V\right\vert =\left\vert W\right\vert \) なら、\(V\) から \(W\) への任意の全単射が同型写像となる。空グラフに対しても同様のことが言える。

2.6.2路グラフと閉路グラフ

続いて、単純な形をしたグラフの族を定義する:

定義 2.6.2

任意の \(n \in \mathbb{N}\) に対して、単純グラフ

\[ \begin{aligned} & \left( \left\{ 1,2,\ldots,n\right\} ,\ \ \left\{ \left\{ i,i+1\right\} \mid 1\leq i < n\right\} \right) \\ & \quad =\left( \left\{ 1,2,\ldots,n\right\} ,\ \ \left\{ 12,\ 23,\ 34,\ \ldots ,\ \left( n-1\right) n\right\} \right) \end{aligned} \]

を \(n\) 次の路グラフ (\(n\)-th path graph) と呼び、\(P_{n}\) と書く。

このグラフは \(n\) 個の頂点と \(n-1\) 個の辺を持つ (\(n=0\) のときは例外で、辺を持たない)。

定義 2.6.3

任意の自然数 \(n > 1\) に対して、単純グラフ

\[ \begin{aligned} & \left( \left\{ 1,2,\ldots,n\right\} ,\ \ \left\{ \left\{ i,i+1\right\} \mid 1\leq i < n \right\} \cup\left\{ \left\{ n,1\right\} \right\} \right) \\ & \quad =\left( \left\{ 1,2,\ldots,n\right\} ,\ \ \left\{ 12,\ 23,\ 34,\ \ldots ,\ \left( n-1\right) n,\ n1\right\} \right) \end{aligned} \]

を \(n\) 次の閉路グラフ (\(n\)-th cycle graph) と呼び、\(C_{n}\) と書く。

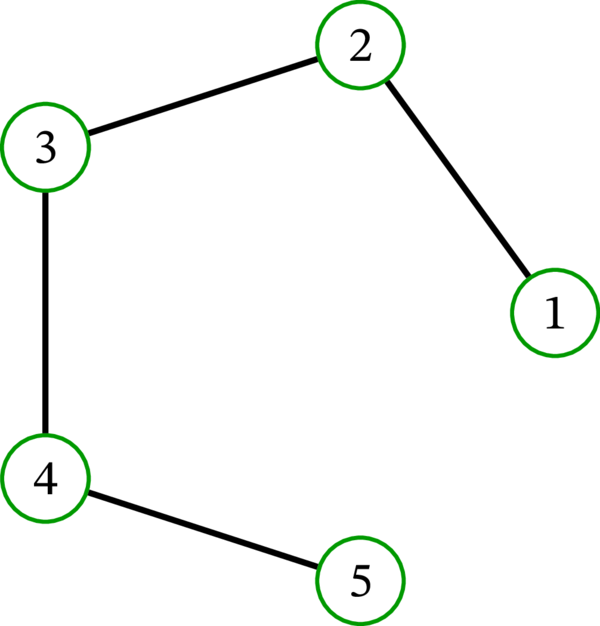
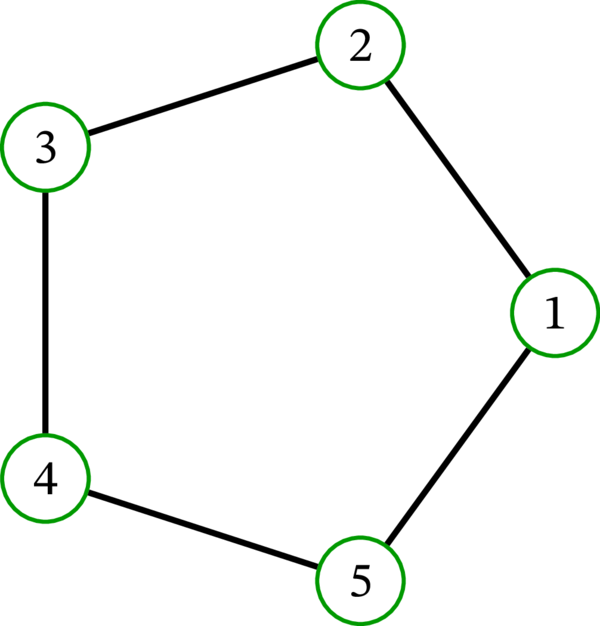
このグラフは \(n\) 個の頂点と \(n\) 個の辺を持つ (\(n=2\) のときは例外で、辺を \(1\) 個しか持たない)。 [後に \(2\) 次の閉路グラフ \(C_{2}\) の定義は \(2\) 個の辺を持つように変更される。ただし \(2\) 頂点の単純グラフが \(2\) 個の辺を持つことはできないので、今はこの変更を行えない。]

路グラフ \(P_{5}\) と閉路グラフ \(C_{5}\) の描画を示す:

もちろん、路グラフは水平に伸ばした状態で描画されることが多い:

なお、閉路グラフ \(C_{3}\) は完全グラフ \(K_{3}\) と一致する。

質問: \(P_{n}\) からそれ自身へのグラフ同型写像を答えよ。

解答: 恒等写像 \(\operatorname*{id}\colon\left\{ 1,2,\ldots,n\right\} \rightarrow\left\{ 1,2,\ldots,n\right\} \) は \(P_{n}\) からそれ自身へのグラフ同型写像である。また、次の「反転」写像も \(P_{n}\) からそれ自身へのグラフ同型写像となる:

\[ \begin{aligned} \left\{ 1,2,\ldots,n\right\} & \rightarrow\left\{ 1,2,\ldots,n\right\} \\ i & \mapsto n+1-i \end{aligned} \]

この二つ以外に \(P_{n}\) からそれ自身へのグラフ同型写像は存在しない。

質問: \(C_{n}\) からそれ自身へのグラフ同型写像を答えよ。

解答: 任意の \(k\in\mathbb{Z}\) に対して、次の写像を \(k\) 頂点分の回転 (rotation by \(k\) vertices) と定める:

\[ \begin{aligned} \left\{ 1,2,\ldots,n\right\} & \rightarrow\left\{ 1,2,\ldots,n\right\} ,\\ i & \mapsto\left( \left\{ 1,2,\ldots,n\right\} \text{ の第 } i+k\ \text{ mod } n\text{ 要素} \right) \end{aligned} \]

こうすると、\(C_{n}\) の頂点集合に適用できる \(n\) 個 (\(k\in\left\{ 1,2,\ldots,n\right\} \) のそれぞれに対して一つずつ) の回転が手に入る。これらは全て \(C_{n}\) からそれ自身へのグラフ同型写像である。

この他にも、頂点の並びを反転させる次の写像も条件を満たすグラフ同型写像となる:

\[ \begin{aligned} \left\{ 1,2,\ldots,n\right\} & \rightarrow\left\{ 1,2,\ldots,n\right\}\\ i & \mapsto\left(\left\{ 1,2,\ldots,n\right\} \text{ の第 } k - i\ \text{ mod } n \text{ 要素} \right) \end{aligned} \]

ここで \(k\in\mathbb{Z}\) である。この形をした \(C_{n}\) からそれ自身へのグラフ同型写像も \(n\) 個ある。

\(C_{n}\) からそれ自身へのグラフ同型写像はここに示した計 \(2n\) 個で全てであり、他には存在しない。 [この \(2n\) 個の写像は \(n\) 次の二面体群 (dihedral group) を構成する。]

2.6.3Kneser グラフ

次に定義するグラフの族は今までのものより豪華な定義を持つ:

定義 2.6.4

\(S\) を有限集合、\(k \in \mathbb{N}\) とする。このとき、単純グラフ

\[ K_{S,k}\colonequals \left( \mathcal{P}_{k}\left( S\right) ,\ \ \left\{ IJ\ \mid \ I,J\in\mathcal{P}_{k}\left( S\right) \ \wedge\ I\cap J=\varnothing \right\} \right) \]

を \(S\) の \(k\) 次 Kneser グラフ (\(k\)-th Kneser graph of \(S\)) と定義する。\(K_{S,k}\) の頂点は \(k\) 個の要素を持つ \(S\) の部分集合であり、二つの部分集合が共通要素を持たないとき、かつそのときに限って対応する頂点が辺で結ばれる。

グラフ \(K_{\left\{ 1,2,\ldots,5\right\} ,2}\) は Petersen グラフ (Petersen graph) と呼ばれる。Petersen グラフの描画を次に示す:

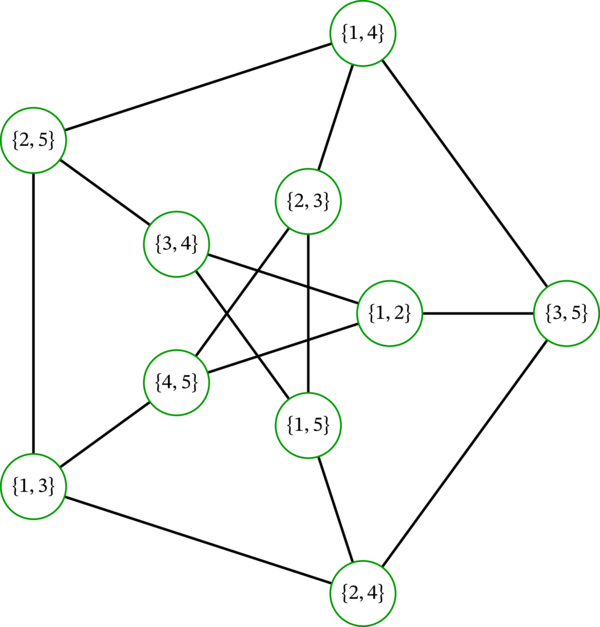
Petersen グラフの頂点は \(\left\{ 1,2,\ldots,5\right\}\) の二要素部分集合であり、二頂点は共通要素を持たないとき、かつそのときに限って隣接する。