2.10. グラフの閉歩道と閉路

特別な歩道を二つ定義する:

例 2.10.2

\(G\) を次の単純グラフとする:

\[ \left( \left\{ 1,2,3,4,5,6\right\} ,\ \ \left\{ 12,\ 23,\ 34,\ 45,\ 56,\ 61,\ 13\right\} \right) \]

[このグラフは過去に例 2.9.2 で見た。] \(G\) の描画を示す:

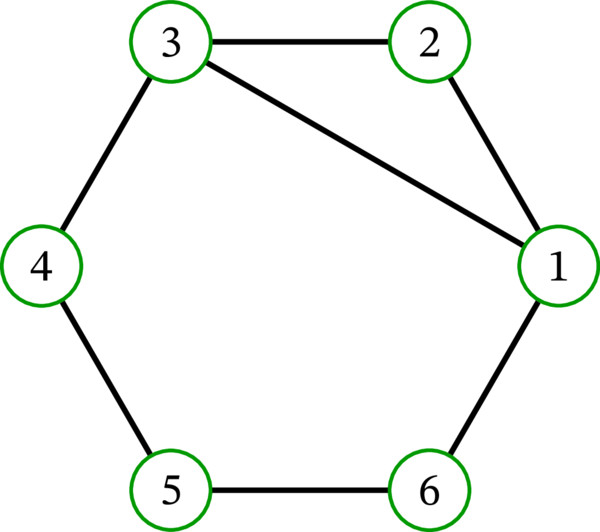
このとき:

• 列 \(\left( 1,3,2,1,6,5,6,1\right) \) は \(G\) の閉歩道である。しかし閉路ではない。

• 列 \(\left( 1,2,3,1\right) \), \(\left( 1,3,4,5,6,1\right) \), \(\left( 1,2,3,4,5,6,1\right) \) はどれも \(G\) の閉路である。列を適切に「回転」させれば異なる閉路が得られる (例えば \(\left( 1,2,3,1\right) \) からは \(\left( 2,3,1,2\right) \) と \(\left( 3,1,2,3\right) \) が得られる)。さらに、閉路を反転させることでも異なる閉路が得られる。\(G\) が持つ全ての閉路は以上の操作で得られる。

• 列 \(\left( 1\right) \) と \(\left( 1,2,1\right) \) はどちらも \(G\) の閉歩道であるものの、閉路ではない (「\(k \geq 3\)」の条件を満たさない)。

• \(\left( 1,2,3\right) \) は歩道であるものの、\(1 \neq 3\) なので閉歩道ではない。

\(\left( 1,2,3,1\right) \) と \(\left( 1,3,2,1\right) \) を異なる閉路としてカウントするかどうかについて統一された意見は存在しない。ただ幸いにも、これは閉路を数えるときにだけ問題となり、閉路の (非) 存在を考えるときは問題とならない。

本書ではこれまでに (任意のグラフにおける) 路と路グラフ \(P_{n}\) を定義した。また、(任意のグラフにおける) 閉路と閉路グラフ \(C_{n}\) も定義した。名前が似ていること以外に、これらの概念に関連性はあるだろうか？ 答えは「Yes」である:

[証明] 易しい。□

閉路を含むグラフもあれば、閉路を含まないグラフもある。例えば、完全グラフ \(K_{n}\) は (\(n \geq 3\) のとき) 多数の閉路を含むのに対して、路グラフ \(P_{n}\) は閉路を一つも持たない。グラフが閉路を持つかどうかを判定する基準を見つけてみよう¹:

[命題 2.10.4 の証明] \(\mathbf{w}\) が路でないと仮定する。このとき \(\mathbf{w}\) が閉路を含むと示す必要がある。

\(\mathbf{w}=\left( w_{0},w_{1},\ldots,w_{k}\right) \) とする。\(\mathbf{w}\) が路でないから、\(w_{0},w_{1},\ldots,w_{k}\) は同じ頂点を含む。つまり、\(i < j\) と \(w_{i}=w_{j}\) を満たす整数 \(i\), \(j\) の組が存在する。そのような組の中で、差 \(j - i\) が最小のものを選ぶ。これから \(\left( w_{i},w_{i+1},\ldots,w_{j}\right) \) が閉路であることを示す。

まず、この歩道は \(w_{i} = w_{j}\) より閉歩道である。後は「\(j - i \geq 3\)」と「頂点 \(w_{i},w_{i+1},\ldots,w_{j-1}\) が相異なる」を示せばよい。後者は \(j - i\) の最小性から従う。\(j - i \geq 3\) は背理法で示す。\(j - i\) が \(1\) または \(2\) だと仮定する (\(i < j\) なので、\(j - i\) はこれ以外の値とならない)。\(G\) は単純グラフより辺の端点は必ず異なるので、\(j - i\) は \(1\) にならない。よって \(j - i\) は \(2\) と分かる。しかし、このとき二つの辺 \(w_{i}w_{i+1}\) と \(w_{i+1}w_{i+2}\) は同一となり、\(\mathbf{w}\) の隣接する二辺が全て異なるという事実と矛盾する。矛盾が生じたので \(j - i \geq 3\) であり、証明は完了した。□

[証明] \(\mathbf{w}\) は路でないので、命題 2.10.4 から従う。□

[証明] 示すべき命題の「路」を「バックトラックフリー歩道」に置き換えた、より一般的な命題を示す。ここで「バックトラックフリー歩道 (backtrack-free walk)」とは、隣接する二辺が全て異なる歩道を言う。この命題が示すべき命題の一般化であることは、全ての路がバックトラックフリー歩道である [なぜ？] 事実から分かる。

これから次の命題を証明する:

Claim 1 の証明は \(\mathbf{p}\) の長さに関する数学的帰納法で行う。整数 \(N\) を固定し、\(\mathbf{p}\) の長さが \(N-1\) の場合に Claim 1 が成り立つと仮定する。この上で \(\mathbf{p}\) の長さが \(N\) のときにも Claim 1 が正しいことを示す。

\(a=N\) として、\(\mathbf{p}=\left( p_{0},p_{1},\ldots,p_{a}\right) \) と \(\mathbf{q}=\left( q_{0},q_{1},\ldots,q_{b}\right) \) を同じ頂点から始まって同じ頂点で終わる相異なる二つのバックトラックフリー歩道とする。 このとき、\(G\) が閉路を持つことを示せばよい。

\(\mathbf{p}\) と \(\mathbf{q}\) は同じ頂点から始まる相異なる歩道なので、両方とも自明²な歩道であることはない。また、もし片方が自明な歩道なら、自明な歩道は閉歩道なのでもう一方も閉歩道となる。つまり \(G\) は非自明かつバックトラックフリー歩道である閉歩道を持つので、系 2.10.6 から \(G\) が閉路を持つと結論できる。よって以降の議論では、\(\mathbf{p}\) と \(\mathbf{q}\) がいずれも自明でないと仮定する。このとき \(\mathbf{p}\) と \(\mathbf{q}\) には最後の辺が存在する。\(\mathbf{p}\) の最後の辺を \(p_{a-1}p_{a}\) として、\(\mathbf{q}\) の最後の辺を \(q_{b-1}q_{b}\) とする。

続いて、次の二つの場合を分けて考える:

• Case 1: \(p_{a-1}p_{a}=q_{b-1}q_{b}\) が成り立つ。

• Case 2: \(p_{a-1}p_{a} \neq q_{b-1}q_{b}\) が成り立つ。

Case 1 を最初に考える。歩道 \(\mathbf{p}\), \(\mathbf{q}\) の最後の辺 \(p_{a-1}p_{a}\) と \(q_{b-1}q_{b}\) が等しいので、二つの歩道の最後から二つ目の頂点も等しい。\(\mathbf{p}\), \(\mathbf{q}\) から最後の頂点を取り除くと、同じ頂点から始まって同じ頂点で終わる相異なる二つのバックトラックフリー歩道 \(\left( p_{0},p_{1},\ldots,p_{a-1}\right) \) と \(\left( q_{0},q_{1},\ldots,q_{b-1}\right) \) が得られる。前者の長さは \(a-1=N-1\) なので、帰納法の仮定より、(\(\mathbf{p}\) と \(\mathbf{q}\) ではなく) この二つの歩道になら Claim 1 を適用できる。よって \(G\) は閉路を持つと結論でき、Case 1 における証明は完了する。

続いて Case 2 を考える。二つの歩道 \(\mathbf{p}\) と \(\mathbf{q}\) (正確には \(\mathbf{p}\) と、\(\mathbf{q}\) の反転) を連結すると、次の歩道 \(\mathbf{r}\) が得られる:

\(\left( p_{0},p_{1},\ldots ,p_{a}\right) \) と \(\left( q_{0},q_{1},\ldots,q_{b}\right) \) がバックトラックフリー歩道であり、さらに \(p_{a-1}p_{a}\neq q_{b-1}q_{b}\) なので、\(\mathbf{r}\) もバックトラックフリー歩道である。また、\(\mathbf{r}\) は少なくとも辺 \(p_{a-1}p_{a}\) を含むので、\(\mathbf{r}\) の長さは \(0\) より大きい。よって系 2.10.6 から \(G\) が閉路を持つと分かる。

Case 1 と Case 2 の両方で \(G\) の閉路が見つかったので、数学的帰納法の帰納ステップが完了した。以上で Claim 1 は証明された。上述したように、定理 2.10.7 は Claim 1 から従う。□