2.4. グラフの頂点の次数

単純グラフの頂点の次数とは、その頂点を含む辺の個数を言う:

定義 2.4.1

\(G=\left( V,E\right) \) を単純グラフとする。\(G\) の頂点 \(v \in V\) の次数 (degree) は次のように定義される:

\[ \begin{aligned} v\colonequals & \ \left( v \text{ を含む辺 } e\in E \text{ の個数} \right) \\ = & \ \left( v \text{ の隣接頂点の個数}\right) \\ = & \ \left\vert \left\{ u\in V\mid uv\in E\right\} \right\vert \\ = & \ \left\vert \left\{ e\in E\mid v\in e\right\} \right\vert \end{aligned} \]

定義 2.4.1 の最後に示した変形の正しさは非常に簡単に確認できる: 頂点 \(v\) を含む辺 \(e \in E\) は \(v\) の隣接頂点をちょうど一つ含む。逆に、\(v\) の隣接頂点と \(v\) からなる辺は \(v\) の隣接頂点ごとにちょうど一つ存在する。ただし、この変形が可能なのは単純グラフを考えているときだけであり、多重グラフを考えるときは行えない。

例として、次のグラフを考える:

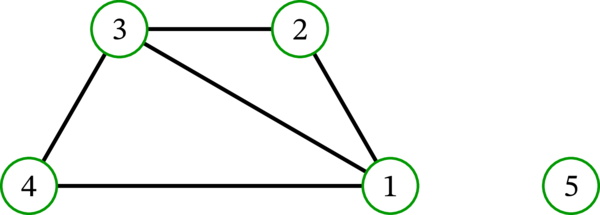
このグラフの各頂点の次数は次の通りである:

\[ \begin{aligned} \deg1 &= 3,\quad \deg2 = 2,\quad \deg3 = 3, \\ \deg4 &= 2,\quad \deg5 = 0 \end{aligned} \]

単純グラフの次数に関する基本的な性質をいくつか示す:

命題 2.4.2

\(G\) を \(n\) 頂点の単純グラフとする。\(v\) を \(G\) の頂点とするとき、次が成り立つ:

\[ \deg v\in\left\{ 0,1,\ldots,n-1\right\} \]

[証明] \(v\) の隣接頂点は全て集合 \(\operatorname*{V}\left( G\right) \setminus\left\{ v\right\} \) に属する。この集合の大きさは \(n-1\) なので、\(v\) の次数も \(n-1\) 以下となる。□

命題 2.4.3

[Euler 1736] \(G\) を単純グラフとする。\(G\) の頂点の次数の和は、\(G\) の辺の個数の二倍に等しい。言い換えれば、次の等式が成り立つ:

\[ \sum_{v\in\operatorname*{V}\left( G\right) }\deg v=2\cdot\left\vert \operatorname*{E}\left( G\right) \right\vert \]

[証明] \(G=\left( V,E\right) \) とする。つまり \(V = \operatorname*{V}\left( G\right)\) および \(E = \operatorname*{E}\left( G\right)\) と定める。

\(v \in e\) を満たす \(\left( v,e\right) \in V\times E\) の個数を \(N\) とする。これから \(N\) を二つの異なる方法で計算する。 [この証明手法は二重数え上げ (double-counting) と呼ばれる。]

それぞれの頂点 \(v \in V\) に対して \(v \in e\) を満たす \(e \in E\) の個数を考え、その和として \(N\) を求める。頂点 \(v\) に対する「\(v \in e\) を満たす \(e \in E\) の個数」は次数の定義そのものなので、和 \(N\) は \(\sum\limits_{v\in V}\deg v\) と書ける。
一方、それぞれの \(e \in E\) に対して \(v \in e\) を満たす \(v \in V\) の個数を考え、その和として \(N\) を求める。全ての \(e \in E\) は \(V\) に含まれる頂点をちょうど二つ持つので、その和 \(N\) は \(\sum\limits_{e\in E}2=\left\vert E\right\vert \cdot 2=2\cdot\left\vert E\right\vert \) と書ける。

二つの和はどちらも \(N\) に等しいので \(\sum\limits_{v\in V}\deg v=2\cdot\left\vert E\right\vert \) が分かる。これが示したい等式だったから、命題 2.4.3 は証明された。□

系 2.4.4

[握手補題] \(G\) を単純グラフとする。\(G\) の頂点 \(v\) で次数 \(\deg v\) が奇数であるものは偶数個存在する。

[証明] 命題 2.4.3 より \(\sum\limits_{v\in \operatorname*{V}\left( G\right) }\deg v=2\cdot\left\vert \operatorname*{E}\left( G\right) \right\vert \) なので、\(\sum\limits_{v\in\operatorname*{V}\left( G\right) }\deg v\) は偶数だと分かる。整数の和が偶数のとき、足される整数に含まれる奇数は偶数個である。よって和 \(\sum \limits_{v\in\operatorname*{V}\left( G\right) }\deg v\) で足されている整数には奇数が偶数個含まれる。言い換えれば、\(G\) の頂点 \(v\) で次数 \(\deg v\) が奇数なものは偶数個存在する。□

系 2.4.4 は「人が何人か集まったとき、その中にいる友人の数が奇数の人の数は偶数である」と表現されることがしばしばある。系 2.4.4 は握手補題 (handshake lemma) と呼ばれる。

単純グラフにおける次数の性質をもう一つ示す:

命題 2.4.5

二個以上の頂点を持つ単純グラフを \(G\) とする。このとき、同じ次数を持つ相異なる \(G\) の二頂点 \(v\), \(w\) が存在する。

[証明] 背理法で示す。\(n=\left\vert \operatorname*{V}\left( G\right) \right\vert \) として、\(G\) の \(n\) 頂点が全て異なる次数を持つと仮定する。

この仮定を言い換えれば、写像

\[ \begin{aligned} \deg\colon \operatorname*{V}\left( G\right) & \rightarrow\left\{ 0,1,\ldots ,n-1\right\} \\ v & \mapsto\deg v \end{aligned} \]

は単射である。この写像は同じ大きさ (\(n\) 要素) の有限集合間の写像なので、鳩の巣原理より単射であるなら全単射でなければならない。よって、この写像によって \(0\) および \(n-1\) に移される頂点が存在する。

つまり、次数が \(0\) の頂点 \(u\) と次数が \(n-1\) の頂点 \(v\) が存在する。\(u\) と \(v\) の間に辺は存在するだろうか？ \(\deg v = n-1\) によれば存在し、\(\deg u = 0\) によれば存在しない。矛盾だ！ □

[注意: \(0 \neq n-1\) なので、二つの頂点 \(u\), \(v\) は相異なる。「頂点が二つ以上ある」という仮定はここで使われている！]

隣接頂点の数え上げを応用して単純グラフに関する事実を証明する例として、Mantel の定理と呼ばれる命題の証明を示す:

定理 2.4.6

[Mantel の定理 (Mantel's theorem)] \(G\) を \(n\) 個の頂点と \(e\) 個の辺を持つ単純グラフとする。\(e>n^{2}/4\) が成り立つなら、\(G\) は三角形 (相互に隣接する三つの相異なる頂点) を持つ。

例 2.4.7

\(V\) と \(E\) を次のように定め、単純グラフ \(G = \left( V,E\right)\) を定義する:

\[ \begin{aligned} V &= \left\{ 1,2,3,4,5,6\right\}\\ E &= \left\{ 12,\ 23,\ 34,\ 45,\ 56,\ 61,\ 14,\ 25,\ 36\right\} \end{aligned} \]

\(G\) の描画を示す:

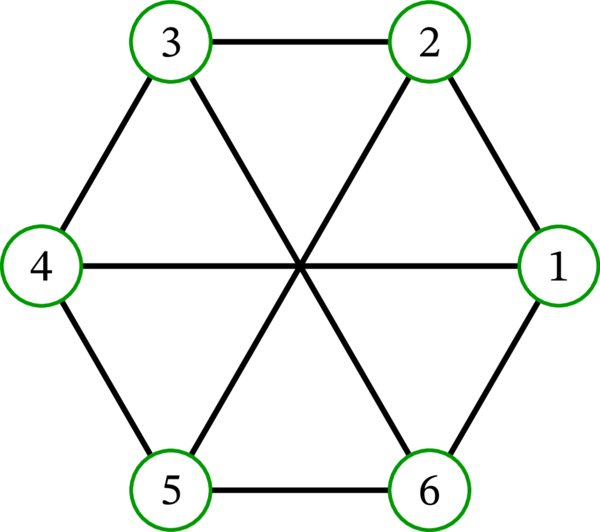
このグラフは三角形を持たない。 [ところで、この事実は \(G\) の全ての辺が偶奇の異なる頂点を結んでいることから簡単に確認できる。もし三角形が存在するなら、偶奇の一致する頂点を結ぶ辺が必ず存在する。] よって Mantel の定理の対偶から、\(n=6\) および \(e=9\) のとき \(e\leq n^{2}/4\) が成り立つと分かる。実際 \(9=6^{2}/4\) なのでこれは正しい。一方、ここからは \(G\) に一本でも辺を加えると三角形が必ず生じることが分かる。

[定理 2.4.6 の証明] \(n\) に関する強い数学的帰納法で示す。頂点の個数が \(n\) より小さい任意の単純グラフで Mantel の定理が成り立つと (帰納法の仮定として) 仮定する。この帰納法の仮定を利用して、\(n\) 個の頂点を持つ単純グラフ \(G\) で Mantel の定理が成り立つことをこれから示す。\(G=\left( V,E\right) \) となるように \(V=\operatorname*{V}\left( G\right) \) および \(E=\operatorname*{E}\left( G\right) \) と定める。

\(e > n^{2}/4\) を満たす \(G\) が三角形を持つことを背理法で示す。\(G\) が \(e > n^{2}/4\) を満たし、三角形を持たないと仮定する。

\(e>n^{2}/4\geq0\) より、\(G\) は辺を持つ。辺を一つ取って \(vw\) とする。このとき \(v \neq w\) である。

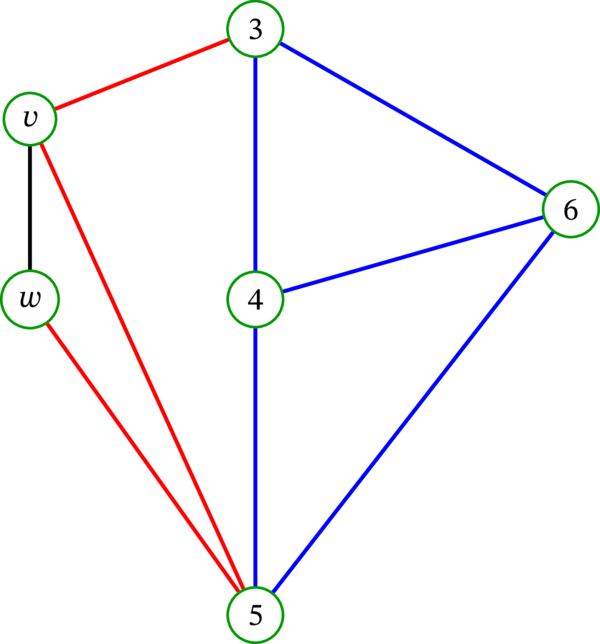
続いて、次の規則に従って \(G\) の辺を三つの色 (黒・青・赤) のいずれかで塗る:

\(vw\) は黒で塗る。
\(v\) と \(w\) のいずれか一方だけを含む辺は赤で塗る。
その他の辺は青で塗る。

この彩色の例を示す:

次に、色ごとに辺の個数を数える:

黒で塗られた辺は \(1\) 個ある ── 具体的には \(vw\) である。
赤い辺はいくつあるだろうか？最大でも \(n-2\) 個である。実際、赤い辺は \(v\) と \(w\) 以外の頂点一つごとに最大でも一つしか存在できない: もし二つの赤い辺に含まれる頂点が存在するなら、その頂点と \(v\) と \(w\) が三角形となってしまう。
青い辺はいくつあるだろうか？ \(v\) と \(w\) 以外の頂点およびそれらを接続する青い辺は \(n-2\) 頂点の単純グラフを構成する。このグラフを \(H\) とする。\(G\) が三角形を持たないので、\(H\) も三角形を持たない。帰納法の仮定から、\(H\) が \(\left( n-2\right) ^{2}/4\) より多い辺を持っていれば三角形を持つと分かる。よって \(H\) の辺 (つまり青い辺) の個数は \(\left( n-2\right) ^{2}/4\) 以下と分かる。

まとめると、\(G\) の辺の個数 \(e\) は次の不等式を満たす:

\[ e \leq 1+\left( n-2\right) +\left( n-2\right) ^{2}/4=n^{2}/4 \]

これは \(e>n^{2}/4\) と矛盾するので、\(G\) は三角形を持つ。以上で定理 2.4.6 (Mantel の定理) は証明された。□

質問: 等号は成り立つだろうか？つまり、\(n\) 個の頂点と \(n^{2}/4\) 個の辺からなる、三角形を持たないグラフは存在するだろうか？答えは「\(n\) が偶数なら存在する」である。実際、偶数 \(n\) に対する次のグラフが条件を満たす:

\[ \left( \left\{ 1,2,\ldots,n\right\} ,\ \left\{ ij\mid i\not \equiv j \bmod 2\right\} \right) \]

[この式で \(ij\) が表すのは二要素集合 \(\left\{ i,j\right\}\) であって \(i\) と \(j\) の積でないことに注意してほしい。なお、奇数の \(n\) に対しても同様のグラフを考えることができ、そのとき辺の個数は \(\left( n^{2}-1\right) /4\) となる。\(n\) が奇数のとき、これは \(n^{2}/4\) より小さい最大の整数であり、これ以上辺の個数を増やすことはできない ── 結局、辺の個数は整数でなければならない。] つまり、Mantel の定理が示す下界は (整数だけを考えるとき) 最適である。

次の練習問題は Mantel の定理の「逆バージョン」と言える:

練習問題 2.2

\(n\) 個の頂点と \(e\) 個の辺を持つ単純グラフを \(G\) とする。\(e < n \left( n-2\right) /4\) のとき、\(G\) が反三角形 (どの二点も非隣接な相異なる三頂点) を持つことを示せ。

[解答: これは 2017 年春学期に開講された講義で出した homework set #1 の Exercise 2 である。解答は講義ページに載っている。]

Mantel の定理は次のように一般化できる:

定理 2.4.8

[Turán の定理 (Turán's theorem)] \(r\) を正整数、\(G\) を \(n\) 個の頂点と \(e\) 個の辺を持つ単純グラフとする。このとき

\[ e>\dfrac{r-1}{r}\cdot\dfrac{n^{2}}{2} \]

が成り立つなら、相互に隣接する \(r+1\) 個の相異なる頂点が \(G\) に存在する。

Mantel の定理は Turán の定理で \(r=2\) とした特殊ケースである。Turán の定理は第 7.3 節で証明される。Mantel の定理と Turán の定理は極値グラフ理論 (extremal graph theory) と呼ばれる分野における最も簡単な結果である。極値グラフ理論は、グラフのパラメータ (本節で見たのは頂点の個数と辺の個数) 間の不等式とグラフの小構造 (本節で見たのは三角形と \(r+1\) 個の相互に接続する頂点) の存在に関する関係を扱う。この分野のさらに本格的な入門書として [Zhao23, Chapters 1 and 5] や [Jukna11] がある。

練習問題 2.3

\(G=\left( V,E\right) \) を単純グラフ、\(n=\left\vert V\right\vert \) とする。\(G\) の辺 \(e_{1}, e_{2}, \ldots, e_{k}\) と \(G\) の三角形 \(t_{1}, t_{2}, \ldots, t_{\ell}\) で次の条件を満たすものが存在することを示せ:

\(k+\ell\leq n^{2}/4\)
\(E\setminus\left\{ e_{1},e_{2},\ldots,e_{k}\right\} \) の各辺が三角形 \(t_{1},t_{2},\ldots,t_{\ell}\) のいずれかの部分集合である。

[Remark: 言い換えれば、この命題は \(G\) の全ての辺が \(n^{2}/4\) 個の辺または三角形で被覆できると主張している。ここで辺または三角形 (edge-or-triangle) とは \(G\) の辺または三角形である頂点集合を言い、被覆 (cover) するとは \(G\) の各辺が選択された辺または三角形のいずれかの部分集合であることを言う。]

[ヒント: 上述した Mantel の定理の証明と同様に議論を進める。]

Remark 2.4.9

練習問題 2.3 の命題は Mantel の定理を一般化したものと言える。実際、単純グラフ \(G=\left( V,E\right) \) が三角形を持たないとき練習問題 2.3 の \(\ell\) は \(0\) でなければならず、\(e_{1},e_{2},\ldots,e_{k}\) は \(G\) の全ての辺となる。ここから \(\left\vert E\right\vert =k\leq k+\ell\leq n^{2}/4\) が得られる。

練習問題 2.4

\(n\) 個の頂点と \(k\) 個の辺を持つ単純グラフを \(G\) とする (\(n > 0\))。\(G\) が少なくとも \(\dfrac{k}{3n}\left( 4k-n^{2}\right) \) 個の三角形を持つことを示せ。

[ヒント: \(G\) の辺を任意に取って \(vw\) とするとき、\(v\) と \(w\) を含む三角形が少なくとも \(\deg v + \deg w - n\) 個存在することを最初に示す。次に、\(n\) 個の実数 \(a_{1}, a_{2}, \ldots, a_{n}\) に対する不等式 \(n \left( a_{1}^{2} + a_{2}^{2} + \cdots+ a_{n}^{2} \right) \geq\left( a_{1} + a_{2} + \cdots+ a_{n} \right) ^{2}\) を利用する (この不等式は「Cauchy–Schwarz の不等式」「Chebyshev の不等式」「Jensen の不等式」などと呼ばれる ── 好きな名前を選ぼう！)。]

Remark 2.4.10

練習問題 2.4 の命題は三角形に対する Moon–Moser の不等式 (Moon–Moser inequality for triangles) と呼ばれる。これも Mantel の定理の一般化である: もし \(k > n^{2} / 4\) なら \(\dfrac{k}{3n} \left( 4k-n^{2} \right) > 0\) であり、練習問題 2.4 の命題から \(G\) が少なくとも一つの三角形を持つと分かる。

練習問題 2.5

\(G=\left( V,E\right) \) を単純グラフとする。

\(G\) の辺 \(e=\left\{ u,v\right\} \) が奇数 (odd) であるとは、整数 \(\deg u+\deg v\) が奇数であることを言う。

\(G\) の奇数辺の個数が偶数であることを示せ。

[ヒント: 証明は何通りか考えられる。その一つは合同算術と整数 \(m\) に対する恒等式 \(m^{2} \equiv m \bmod 2\) を利用する。常識だけを使う証明もある。]

練習問題 2.6

\(G=\left( V,E\right) \) を単純グラフとする。\(V\) の部分集合 \(S\) を任意に取り、\(k=\left\vert S\right\vert \) と定める。次の不等式を示せ:

\[ \sum_{v\in S}\deg v\leq k\left( k-1\right) +\sum_{v\in V\setminus S} \min\left\{ \deg v,k\right\} \]

Remark 2.4.11

練習問題 2.6 の命題は仮定を加えれば逆方向にも成り立つ: \(n\) 個の非負整数 \(d_{1},d_{2},\ldots,d_{n}\) が次の条件を全て満たすとする:

\(d_{1}\geq d_{2}\geq\cdots\geq d_{n}\)
\(d_{1}+d_{2}+\cdots+d_{n}\) が偶数
全ての \(k\in\left\{ 1,2,\ldots,n\right\} \) が次の不等式を満たす:
\[ \sum_{i=1}^{k}d_{i}\leq k\left( k-1\right) +\sum_{i=k+1}^{n}\min\left\{d_{i},k\right\} \]

このとき、頂点集合が \(\left\{ 1,2,\ldots ,n\right\} \) で各頂点の次数が \(d_{1},d_{2},\ldots,d_{n}\) である単純グラフが存在する。この結果は Erdős–Gallai の定理 (Erdős–Gallai theorem) と呼ばれる。