2.8. グラフの非交和

既知のグラフから新しいグラフを構築するもう一つの方法として非交和 (disjoint union) がある。非交和のアイデアは簡単に理解できる: いくつかの単純グラフ \(G_{1},G_{2},\ldots,G_{k}\) の非交和 \(G_{1}\sqcup G_{2}\sqcup\cdots\sqcup G_{k}\) とは、全てのグラフを並べて一つの大きなグラフとみなしたものを言う。これを数学的に厳密な定義とするには、グラフ \(G_{i}\) の各頂点 \(v\) を \((i,v)\) に変更して各グラフの頂点集合に含まれる同じ要素を区別する必要がある。例えば、二つの閉路グラフ \(C_{3}\) と \(C_{4}\) の非交和 \(C_{3}\sqcup C_{4}\) は次の「グラフ」であってはならない:

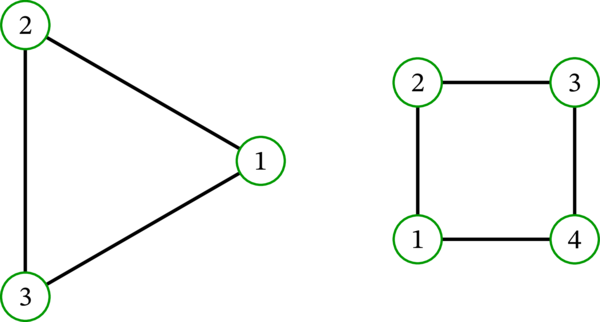
[そもそも、この図はグラフを表していない: グラフは同じ頂点を一つしか持てないにもかかわらず、この図には \(1\) のラベルが付いた点が二つある。] 非交和 \(C_{3}\sqcup C_{4}\) の正しい描画を示す:

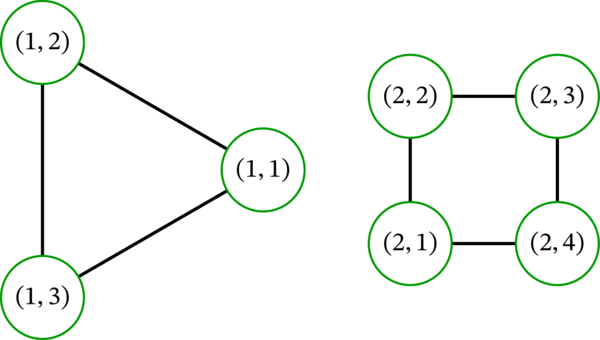
非交和の形式的な定義は次の通りである:

定義 2.8.1

\(G_{1},G_{2},\ldots,G_{k}\) を単純グラフ、\(i\in\left\{ 1,2,\ldots,k\right\} \) に対して \(G_{i}=\left( V_{i}, E_{i}\right) \) とする。次の \(V\), \(E\) を使って定義される単純グラフ \(\left(V,E\right)\) を、\(k\) 個のグラフ \(G_{1},G_{2},\ldots,G_{k}\) の非交和 (disjoint union) と呼び、\(G_{1}\sqcup G_{2}\sqcup\cdots\sqcup G_{k}\) と表す:

\[ \begin{aligned} V & =\left\{ \left( i,v\right) \mid i\in\left\{ 1,2,\ldots,k\right\} \ \wedge\ v\in V_{i}\right\} \\ E & =\left\{ \left\{ \left( i,v_{1}\right) ,\left( i,v_{2}\right) \right\} \mid i\in\left\{ 1,2,\ldots,k\right\} \ \wedge\ \left\{ v_{1},v_{2}\right\} \in E_{i}\right\} \end{aligned} \]

注意: \(G\) と \(H\) を単純グラフとするとき、\(G\sqcup H\) と \(H\sqcup G\) は同型であるものの (\(G = H\) の場合を除けば) 同じではない。例えば、\(C_{3}\sqcup C_{4}\) は頂点 \(\left( 2,4\right) \) を持つのに対して、\(C_{4}\sqcup C_{3}\) は持たない。