2.13. グラフの支配集合

目次

2.13.1定義と基本的な性質

単純グラフに対して定義できる概念をもう一つ示す:

定義 2.13.1

\(G=\left( V,E\right) \) を単純グラフとする。

\(V\) の部分集合 \(U\) が条件「任意の頂点 \(v \in V \setminus U\) が \(U\) に属する隣接頂点を少なくとも一つ持つ」を満たすとき、\(U\) は \(G\) に対して支配的 (dominating) と言う。

\(G\) に対して支配的な \(V\) の部分集合を \(G\) に対する支配集合 (dominating set for \(G\)) と呼ぶ。単に \(G\) の支配集合 (dominating set of \(G\)) とも呼ぶ。

例 2.13.2

次の閉路グラフ \(C_{5}\) を考える:

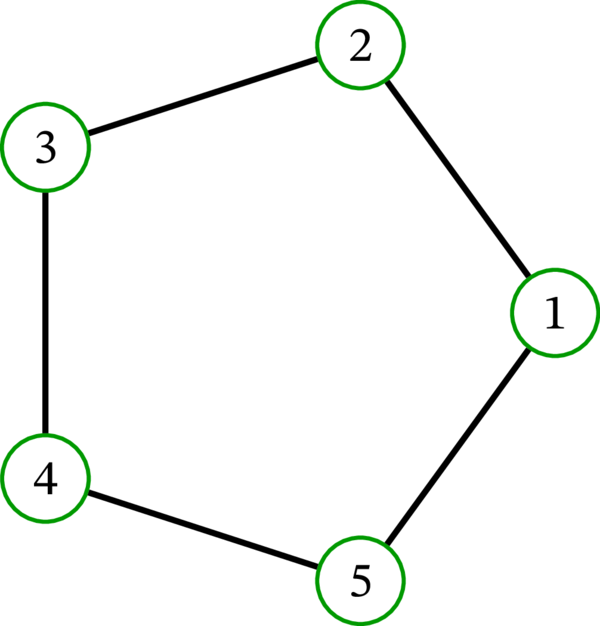
\[ C_{5}=\left( \left\{ 1,2,3,4,5\right\} ,\ \ \left\{ 12,\ 23,\ 34,\ 45,\ 51\right\} \right) \]

集合 \(\left\{ 1,3\right\} \) は \(C_{5}\) の支配集合である。実際、\(\left\{ 1,3\right\} \) に属さない三つの頂点 \(2,4,5\) はいずれも \(\left\{ 1,3\right\} \) に属する隣接頂点を持つ。集合 \(\left\{ 1,5\right\} \) は \(C_{5}\) の支配集合ではない。なぜなら、頂点 \(3\) が \(\left\{ 1,5\right\} \) に属する隣接頂点を持たないためである。\(G\) に要素数が \(0\) または \(1\) の支配集合は存在しない。要素数が \(2\) の支配集合はいくつか存在し、要素数が \(3\) 以上の頂点集合の部分集合は全て支配集合となる。

さらにいくつか例を示す:

明らかに、支配的な集合はグラフが「密」な (辺が多い) ほど見つけやすくなる。与えられたグラフが持つ要素数最小の支配集合に注目する場面がよくある1。空グラフのケースを見れば分かるように、頂点集合全体を支配集合として選ばなければならない状況も存在する。しかし、多くのケースではそれより優れた (要素数の少ない) 支配集合を見つけることができる。ここで、今後の議論で有用な概念を一つ定義する:

定義 2.13.3

\(G\) の単純グラフとする。\(G\) の頂点 \(v\) が隣接頂点を持たない (\(\deg v = 0\) を満たす) とき、\(v\) は孤立 (isolated)していると言う。

孤立した頂点は任意の支配集合に属する (そうでなければ隣接頂点が支配集合に含まれるが、孤立した頂点は隣接頂点を持たない)。そのため、支配集合を議論する上で孤立した頂点を考えても支配集合のサイズが増えるだけであまり意味がない。そこで、支配集合に関する問題では孤立した頂点を持たないグラフだけを考える場合が多い。この条件があると、次の結果が得られる:

命題 2.13.4

\(G=\left( V,E\right) \) を孤立した頂点を持たない単純グラフとする。このとき:

  1. 要素数が \(\left\vert V\right\vert /2\) 以下の支配集合が存在する。

  2. \(A\cap B= \varnothing\) かつ \(A\cup B=V\) を満たす二つの支配集合 \(A\), \(B\) が存在する。

この命題の証明は練習問題 2.19 で考える。[17s, § 3.6] に別証明がある。

特定のグラフを仮定すると命題 2.13.4 (a) にある上界 \(\left\vert V\right\vert /2\) を改善できる場合がよくある。この例を示す:

練習問題 2.17

\(n \geq 3\) を整数とする。閉路グラフ \(C_{n}\) に対する支配集合の最小要素数を求める式を示せ。解答の式では天井関数 (ceiling function) \(x\mapsto\left\lceil x\right\rceil \) を使って構わない。天井関数は実数 \(x\) を \(x\) 以上の最小の整数に変換する。

練習問題 2.18

整数 \(n\), \(k\) が \(k > 1\) と \(n\geq k\left( k+1\right) \) を満たすと仮定する。単純グラフ \(KG_{n,k}\) を集合 \(\left\{1,2,\ldots,n\right\}\) の \(k\) 次 Kneser グラフ \(K_{\left\{1,2,\ldots,n\right\},k}\) と定める (Kneser グラフは定義 2.6.4 で定めた)。つまり、\(KG_{n,k}\) の頂点は \(\left\{ 1,2,\ldots,n\right\} \) の \(k\) 要素部分集合であり、辺は \(A\cap B=\varnothing\) を満たす二頂点 \(A\), \(B\) からなる集合 \(\left\{ A,B\right\} \) である。

\(KG_{n,k}\) の支配集合の最小要素数が \(k + 1\) だと示せ。

練習問題 2.19

\(G=\left( V,E\right) \) を二個以上の頂点を持つ連結な単純グラフとする。

二頂点 \(u\), \(v\) 間の距離 (distance) \(d\left(v,w\right)\) は、\(v\) から \(w\) への路の長さの最小値と定義される (特に、任意の頂点 \(v \in V\) で \(d\left(v,v\right) = 0\) が成り立つ)。

頂点 \(v \in V\) を固定し、\(V\) の部分集合 \(A\), \(B\) を次のように定義する:

\[ \begin{aligned} A &= \left\{ w \in V \mid d\left( v, w \right) \text{ が偶数} \right\} \\ B &= \left\{ w \in V \mid d\left( v, w \right) \text{ が奇数} \right\} \end{aligned} \]

  1. \(A\) が支配的だと示せ。

  2. \(B\) が支配的だと示せ。

  3. 要素数が \(\left| V \right| /2\) 以下の \(G\) の支配集合が存在することを示せ。

  4. \(G\) が連結と仮定しなくても、\(G\) の全ての頂点が少なくとも一つの隣接頂点を持つ限り (c) の命題が成り立つことを示せ (言い換えれば、命題 2.13.4 を証明せよ)。

2.13.2支配集合の個数

続いて、グラフの支配集合の個数に関する最近示された驚くべき結果を紹介する:

定理 2.13.5

[Brouwer の支配集合定理 (Brouwer's dominating set theorem)] \(G\) を単純グラフとする。\(G\) の支配集合の個数は奇数である。

Brouwer のノート [Brouwer09] には、この定理の証明が三つ示されている2。ここには著者が気に入っている証明を示す。まずは新しい用語が必要になる:

定義 2.13.6

\(G=\left( V,E\right) \) を単純グラフとする。共通要素を持たない二つの \(V\) の部分集合 \(A\), \(B\) が条件「\(a \in A\) かつ \(b \in B\) となる辺 \(ab \in E\) が存在しない」を満たすとき、組 \(\left(A, B\right)\) を孤立組 (detached pair) と呼ぶ。

例 2.13.7

閉路グラフ \(C_{6}\) を考える:

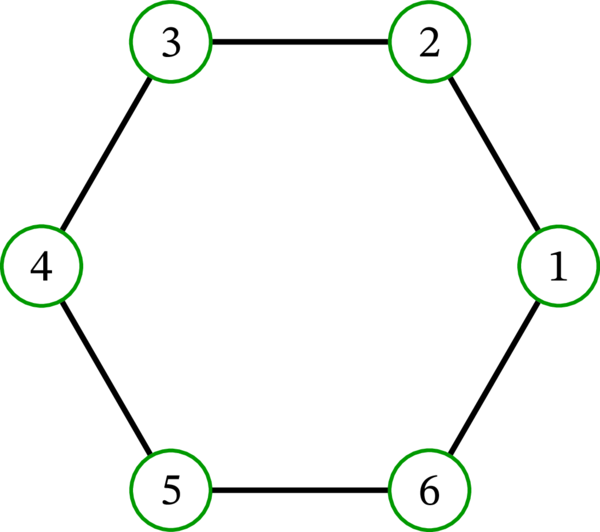
\[ C_{6}=\left( \left\{ 1,2,3,4,5,6\right\} ,\ \left\{ 12,\ 23,\ 34,\ 45,\ 56,\ 61\right\} \right) \]

このとき \(\left( \left\{ 1,2\right\} ,\left\{ 4,5\right\} \right) \) は孤立組であるのに対して、\(\left( \left\{ 1,2\right\} ,\left\{ 3,4\right\} \right) \) は (辺 \(23\) が存在するので) 孤立組でない。もちろん、孤立組は他にも多数存在する: 例えば、\(\left( \varnothing ,B\right) \) や \(\left( A,\varnothing\right) \) の形をした組は全て孤立組である。

ここで、特に断りのない限り「組」が「順序付き組」を意味することを強調しておく。そのため、もし \(\left( A,B\right) \) が孤立組なら、\(\left( B,A\right) \) は異なる孤立組である (ただし \(A=B=\varnothing\) の場合は例外的に同じになる)。

これから定理 2.13.5 の証明のようなものを示す。これは既知の結果を新しいグラフに適用して新しい結果を得る良い例である。ただ問題は、定理の主張と正反対の命題が証明されることである...。

[定理 2.13.5 の証明 (？)] \(G = \left( V,E\right)\) とする。

\(\mathcal{P}\left( V\right) \) は \(V\) の部分集合全体からなる集合を表すことを思い出してほしい。

\(\mathcal{P}\left( V\right) \) を頂点集合とする新しいグラフ \(H\) を次のように構築する: \(V\) の部分集合 \(A\), \(B\) は、\(\left( A,B\right) \) が孤立組であるとき、かつそのときに限って \(H\) で隣接する。 [元々のグラフ \(G\) が \(n\) 個の頂点を持つとき、このグラフ \(H\) は \(2^{n}\) 個の頂点を持つ。\(H\) は非常に大きい！]

これから「奇数の次数を持つ \(H\) の頂点は \(V\) の支配的な部分集合にちょうど等しい」を示す。言い換えれば、次の命題を示す:

Claim 1: \(A\) を \(V\) の部分集合とする。\(H\) の頂点 \(A\) は、\(A\) が \(G\) の支配集合であるとき、かつそのときに限って次数が奇数となる。

[Claim 1 の証明: \(V\) の部分集合 \(A\) に対して、いずれかの隣接頂点が \(A\) に属する \(G\) の頂点全体の集合を \(N\left( A\right) \) と表す。 [\(A\) と \(N\left( A\right) \) は共通要素を持つ場合もあれば、持たない場合もある。]

\(H\) の定義より、\(H\) の頂点 \(A\) の隣接頂点は「\(\left( A,B\right) \) が孤立組」を満たす \(V\) の部分集合 \(B\) である。孤立組の定義を使って言い換えれば、\(A\) の任意の隣接頂点 \(B\) は \(A\) と共通要素を持たず、\(A\) に属する頂点の隣接頂点を一つも持たない。さらに言い換えれば、\(A\) の任意の隣接頂点 \(B\) は \(A\) と共通要素を持たず、\(N\left( A\right) \) とも共通要素を持たない。つまり \(B\) は \(V\setminus\left( A\cup N\left( A\right) \right) \) の部分集合である。従って、\(H\) の頂点 \(A\) の隣接頂点の個数は \(2^{\left\vert V\setminus\left( A\cup N\left( A\right) \right) \right\vert }\) だと分かる。

\(H\) の頂点 \(A\) の次数は \(H\) における \(A\) の隣接頂点の個数に等しい。よって、\(A\) の次数は \(2^{\left\vert V\setminus\left( A\cup N\left( A\right) \right) \right\vert }\) である。\(2^{k}\) が奇数になるのは \(k=0\) のとき、かつそのときに限るので、\(H\) の頂点 \(A\) の次数が奇数になるのは \(\left\vert V\setminus\left( A\cup N\left( A\right) \right) \right\vert =0\) が成り立つとき、かつそのときに限ると分かる。ここで、条件 \(\left\vert V\setminus\left( A\cup N\left( A\right) \right) \right\vert =0\) は次のように書き換えられる:

\[ \begin{aligned} & \left\vert V\setminus\left( A\cup N\left( A\right) \right) \right\vert =0 \\ & \quad \Longleftrightarrow V\setminus\left( A\cup N\left( A\right) \right) =\varnothing \\ & \quad \Longleftrightarrow V\subseteq A\cup N\left( A\right) \\ & \quad \Longleftrightarrow V\setminus A\subseteq N\left( A\right) \\ & \quad \Longleftrightarrow \text{任意の頂点 }v\in V\setminus A\text{ が }N\left( A\right) \text{ に属する} \\ & \quad \Longleftrightarrow \text{任意の頂点 }v\in V\setminus A \text{ に対して、 } \\ & \quad \qquad \qquad G \text{ における } v \text{ の隣接頂点のいずれかが } A \text{ に属する} \\ & \quad \Longleftrightarrow A\text{ は } G \text{ に対して支配的} \qquad \left( \text{「支配的」の定義より}\right) \end{aligned} \]

よって、\(H\) の頂点 \(A\) の次数が奇数となるのは \(A\) が \(G\) に対して支配的なとき、かつそのときに限ると分かる。以上で Claim 1 は証明された。]

Claim 1 によると、奇数の次数を持つ \(H\) の頂点が \(G\) の支配集合そのものである。しかし握手補題 (系 2.4.4) によれば、任意の単純グラフで次数が奇数の頂点は偶数個だけ存在する。この補題を \(H\) に適用すれば、\(G\) の支配集合の個数は偶数だと結論できる。□

はて？ \(G\) の支配集合の個数は奇数だと示したかったのに、偶数だと証明されてしまった！ どうして正反対の結果が得られたのだろうか？

質問: 上に示した論証の間違いを見つけよ！

余白

何が間違いだったのだろうか？

間違いは \(H\) の定義にある。「\(H\) の頂点は \(V\) の部分集合であり、\(H\) の頂点 \(A\), \(B\) は \(\left( A,B\right) \) が孤立組であるときに限って \(H\) で隣接する」という定義だと、頂点 \(\varnothing\) が自身と隣接してしまう (孤立組の定義を \(\left( \varnothing,\varnothing\right) \) が満たすため)。しかし単純グラフの頂点は自身と隣接できないので、これは単純グラフの定義になっていない。よって \(H\) の定義を少しだけ変える必要がある:

[定理 2.13.5 の正しい証明] \(H\) を上述したように定義する。ただし、\(\varnothing\) は自身と隣接しないものとする。 [孤立組 \(\left( A,B\right) \) が \(A=B\) を満たすのは \(A = B = \varnothing\) のときだけなので、\(\varnothing\) 以外の頂点で問題は起こらない。]

\(V = \varnothing\) のとき示したい定理は明らかなので、一般性を失うことなく \(V \neq \varnothing\) と仮定する。このとき \(\varnothing\) は支配的でない。

Claim 1 は次のように修正される:

Claim 1': \(A\) を \(V\) の部分集合とする。\(H\) の頂点 \(A\) が奇数の次数を持つのは、\(A\) が空集合または \(G\) の支配集合のとき、かつそのときに限る。

Claim 1' は Claim 1 の「証明」と同じように証明できる。ただし \(A = \varnothing\) は個別に考える必要がある (これは難しくない: \(H\) の頂点 \(\varnothing\) は自身を除く全ての頂点と隣接するので、その次数は \(2^{\left\vert V\right\vert }-1\) すなわち奇数である)。

よって握手補題を使えば、空集合と支配集合の個数を合わせると偶数だと分かる。空集合の分だけ \(1\) を引けば、支配集合の個数が奇数だと分かる (空集合は支配的でない)。以上で Brouwer の定理 (定理 2.13.5) は証明された。□

Brouwer の定理には異なる証明がいくつかある。特に優れた証明は Irene Heinrich と Peter Tittmann [HeiTit17, Theorem 8] によって 2017 年に示されたもので、彼らは支配集合の個数を求める明示的な式を求め、そこから個数が奇数だと示した。「孤立組」という言葉を使うと、彼らの結果は次のように表現できる:

定理 2.13.8

[Heinrich–Tittmann の等式 (Heinrich–Tittmann formula)] \(G=\left( V,E\right) \) を \(n > 0\) 個の頂点を持つ単純グラフとする。

\(\left\vert A\right\vert \) と \(\left\vert B\right\vert \) が両方とも正の偶数である孤立組 \(\left( A,B\right) \) の個数を \(\alpha\) とする。

\(\left\vert A\right\vert \) と \(\left\vert B\right\vert \) が両方とも奇数である孤立組 \(\left( A,B\right) \) の個数を \(\beta\) とする。

このとき:

  1. \(\alpha\) と \(\beta\) は偶数である。

  2. \(G\) の支配集合の個数は \(2^{n}-1+\alpha-\beta\) である。

(a) は明らかに分かる: \(\left( A,B\right) \) が孤立組のとき、\(\left( B,A\right) \) も孤立組となる。面白いのは (b) である。長いものの初等的な証明を [17s, § 3.3–§ 3.4] に示してある。

さらに最近になって Heinrich と Tittmann [HeiTit18] は彼らの等式を拡張し、特定の要素数を持つ支配集合の個数を数える等式を示した。彼らの中心的な結果は次の等式である:

練習問題 2.20

\(G=\left( V,E\right) \) を一つ以上の頂点を持つ単純グラフ、\(n=\left\vert V\right\vert \) とする。共通要素を持たない二つの \(V\) の部分集合 \(A\), \(B\) が条件「\(a \in A\) かつ \(b \in B\) を満たす辺 \(ab \in E\) が存在しない」を満たすとき、組 \(\left(A, B\right)\) を孤立組 (detached pair) と呼ぶ。

Heinrich–Tittmann の等式を一般化した次の等式を証明せよ:

\[ \sum_{\substack{G \text{ の支配集合 } S}} x^{\left\vert S\right\vert } =\left( 1+x\right) ^{n}-1+ \sum_{\substack{G \text{ の孤立組 } \left( A,B\right) \text{;}\\[2pt] A\neq\varnothing;\ B\neq\varnothing}}\left( -1\right) ^{\left\vert A\right\vert }x^{\left\vert B\right\vert } \]

[ヒント: これは支配集合の個数を数える Heinrich–Tittmann の等式を一般化したものである。実際、この等式に \(x = 1\) を代入し、\(\left\vert A\right\vert \not \equiv \left\vert B\right\vert \bmod 2\) を満たす孤立組に対応する二つの項を打ち消していけば Heinrich–Tittmann の等式が得られる。証明では [17s] の議論を必要な個所を修正した上でコピーして構わない (補題を使っても構わない ── 証明せずに参照してよい)。]

次の練習問題は定理 2.13.5 の一般化である (\(k=1\) とすれば 定理 2.13.5 が得られる)。

練習問題 2.21

\(k\) を正整数、\(G=\left( V,E\right) \) を単純グラフとする。\(V\) の部分集合 \(U\) が \(k\)-路支配的 (\(k\)-path-dominating) とは、全ての頂点 \(v \in V\) に対して \(v\) から \(U\) に属する頂点までの長さ \(k\) 以下の路が存在すること言う。

\(V\) の \(k\)-路支配的な部分集合の個数が奇数だと示せ。

[ヒント: これは見た目ほど大幅な一般化ではない。最も短い証明は非常に短い。]

[解答: これは 2017 年春学期に開講された講義で出した homework set #1 の Exercise 6 である。解答は講義ページに載っている。]

  1. 要素数最小の支配集合を見つける問題はモバイルネットワーキングで利用されるだろう: 例えば、ネットワーク内の任意のノードで「自身がルーターであるか、ルーターと直に接続 (隣接) している」が成り立つようにルーターの集合を選ぶ状況があるかもしれない。 ↩︎

  2. 他の証明は https://artofproblemsolving.com/community/c6h358772p1960068 にある AoPS のスレッドから確認できる。このスレッドが考えているのはコンテスト用の人工的な問題であるものの、この問題が数論の姿に変装した定理 2.13.5 であることはすぐに分かる。 ↩︎

広告
このページの文章はテキストゆれないくんを使って校正されました。