2.2. グラフの描画

単純グラフをいくつか描画してみよう。

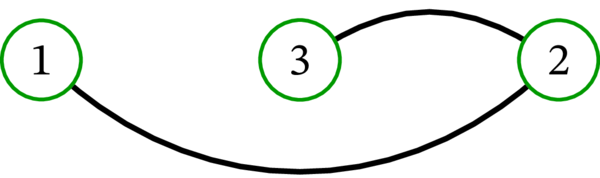
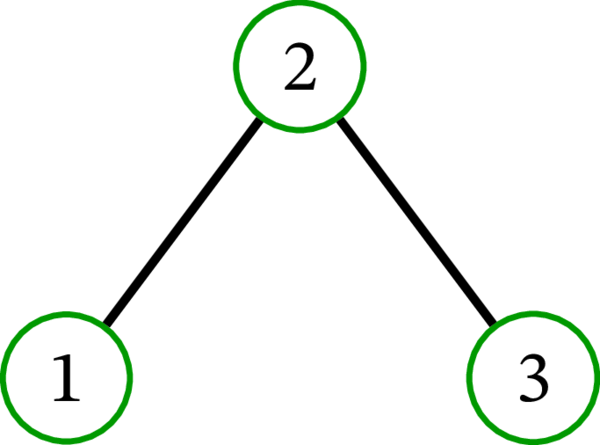
1. 単純グラフ \(\left( \left\{ 1,2,3\right\} ,\ \left\{ 12,23\right\} \right) \) (\(\left\{ u,v\right\} \) を \(uv\) と省略する記法をここでも使っている) は次のように描画できる:

   

   これは (ある意味で) このグラフの最も単純な描画と言える: 辺は直線として表されている。しかし、これ以外の描画も考えられる:

   

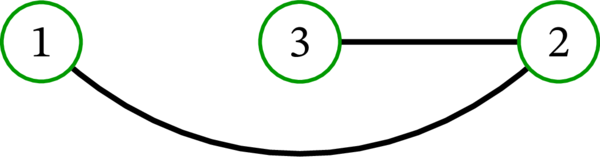
   この描画では頂点 \(1\), \(2\), \(3\) の配置が異なる。その結果として、辺 \(12\) を直線として書くことはできなくなっている: そうすると、書かれる直線は頂点 \(3\) に対応する点を通るので、グラフが曖昧になってしまう (辺 \(12\) が \(13\) と \(32\) という二つの辺と誤解される可能性が生まれる)。

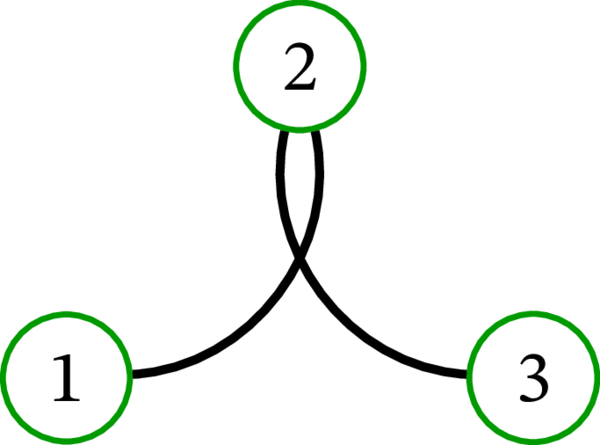
   同じグラフ \(\left( \left\{ 1,2,3\right\} ,\ \left\{ 12,23\right\} \right) \) の異なる描画をさらに三つ示す:

   

   

   

2. 例 2.1.3 では \(n\) 次の共素性グラフ \(\operatorname*{Cop}\nolimits_{n}\) を定義した。\(5\) 次の共素性グラフ \(\operatorname*{Cop}\nolimits_{5}\) の描画の例を次に示す:

   

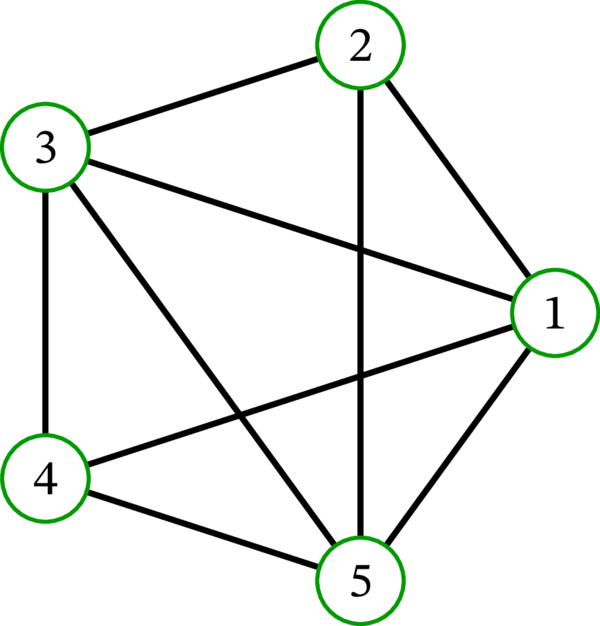
   次に示す \(\operatorname*{Cop}\nolimits_{5}\) の異なる描画では、辺の交差が減っている:

   

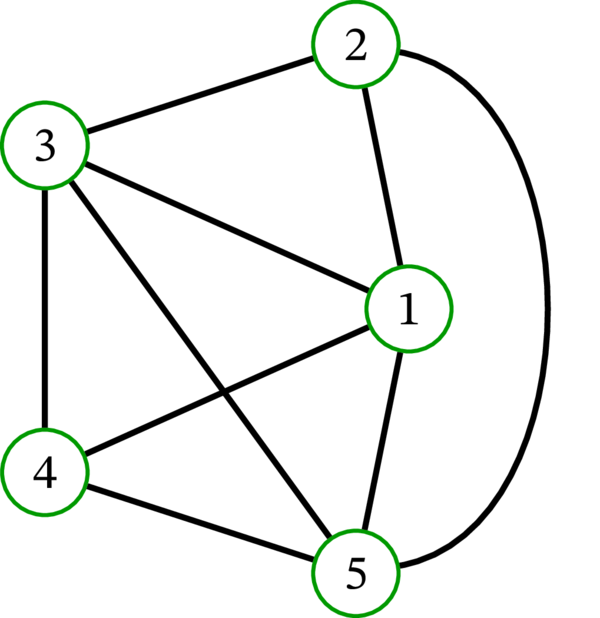
   \(\operatorname*{Cop}\nolimits_{5}\) が持つ五個の頂点の位置を適切に調整すると、どの辺も交差せず、かつ全ての辺を直線にした状態で \(\operatorname*{Cop}\nolimits_{5}\) を描画できる。そのような描画を見つけられるだろうか？

3. さらにもう一つ、単純グラフ \(\left( \left\{ 1,2,3,4,5\right\} ,\ \mathcal{P}_{2}\left( {\left\{ 1,2,3,4,5\right\} }\right) \right) \) の描画を考えよう。これは頂点集合が \(\left\{ 1,2,3,4,5\right\}\) で、辺集合が頂点集合の二要素部分集合全体の単純グラフである (つまり、任意の異なる二頂点が隣接する)。このグラフは後に完全グラフ (complete graph) \(K_{5}\) と呼ばれる。完全グラフ \(K_5\) の描画を示す:

   

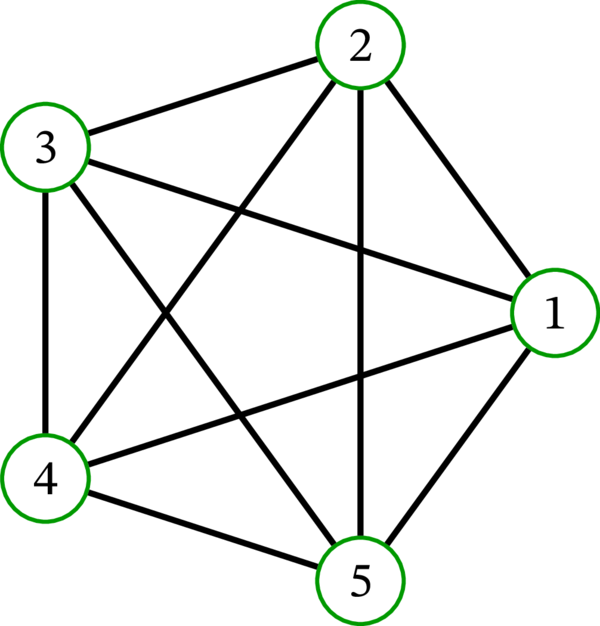
   この描画は様々な用途で有用となる。例えば、このグラフが持つ抽象的な対称性 (頂点 \(1\), \(2\), \(3\), \(4\), \(5\) の全てが「同等」なこと) が描画に現れている。しかしときには、辺の交差を最小化する異なる描画が望まれる場合もある。交差を少なくした \(K_{5}\) の描画を示す:

   

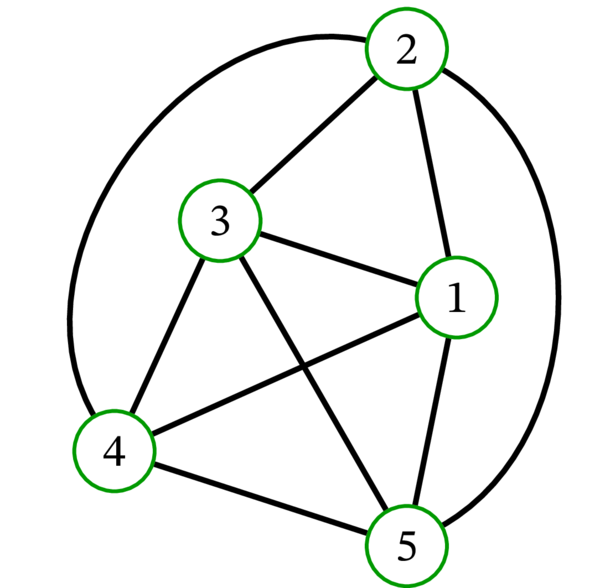
   この描画では、二つの曲線の交差が一つあるだけとなる。では、交差が一つもないように \(K_{5}\) を描画できるだろうか？

   これは組合せ論ではなくトポロジーの問題と言える: 有限集合とグラフではなく平面上の曲線に関する性質が問われている。答えは「No」である。つまり、どのように \(K_{5}\) を平面上に描画したとしても、曲線の交差が少なくとも一つ必ず生じる。これは古典的な結果であり、平面グラフ (planar graph) の理論で最初に学ぶ定理の一つである。証明は様々な教科書に載っている (例えば [FriFri98, Theorem 4.1.2] は、記号の使い方が本書と多少異なるものの、平面グラフ理論の優れた入門書である)。この定理には「平面上の連続曲線」という概念が登場するので、その証明には解析学またはトポロジーを使った議論が必要となる点に注意してほしい (もし曲線が連続でなくても構わないなら、他の曲線を「飛び越す」ことで容易に交差を除去できてしまう！)。