2.14. ハミルトン路とハミルトン閉路

2.14.1定義

話題を変えよう。次の問題を考えてほしい: 単純グラフ \(G\) が与えられたとき、\(G\) の全ての頂点を含む閉歩道を見つけられるのはどんなときだろうか？

答えは簡単に見つかるだろう: 「\(G\) が連結なとき」である。実際、単純グラフ \(G\) の頂点を \(v_{1},v_{2},\ldots,v_{n}\) とすれば、\(G\) が連結より \(v_{1}\) から \(v_{2}\) への歩道、\(v_{2}\) から \(v_{3}\) への歩道、…、\(v_{n-1}\) から \(v_{n}\) への歩道が全て存在する。加えて \(v_{n}\) から \(v_{1}\) への歩道も存在するから、これらの歩道を全て連結すれば \(G\) の全ての頂点を含む閉歩道が得られる。逆に、\(G\) が連結でなければ条件を満たす閉歩道は存在しない。

「閉歩道」を「路」あるいは「閉路」に変えると、この質問はずっと興味深くなる。こういった路と閉路には名前が付いている:

定義 2.14.1

\(G=\left( V,E\right) \) を単純グラフとする。

\(G\) のハミルトン路 (Hamiltonian path) とは、\(G\) の全ての頂点をちょうど一度ずつ含む歩道を言う。明らかに、ハミルトン路は路である。
\(G\) のハミルトン閉路 (Hamiltonian cycle) とは、閉路 \(\left( v_{0},v_{1},\ldots,v_{k}\right) \) であって \(G\) の全ての頂点が \(v_{0},v_{1},\ldots,v_{k-1}\) にちょうど一度ずつ現れるものを言う。

ハミルトン路を持つグラフもあれば持たないグラフもある。ハミルトン閉路を持つことはハミルトン路を持つことより強い条件である: \(\left( v_{0},v_{1},\ldots,v_{k}\right) \) が \(G\) のハミルトン閉路なら、\(\left( v_{0},v_{1},\ldots,v_{k-1}\right) \) は \(G\) のハミルトン路となる。

例 2.14.3

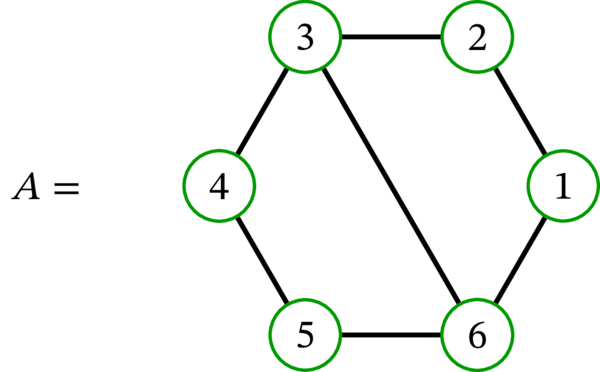
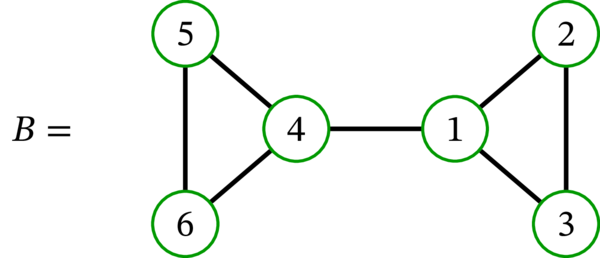
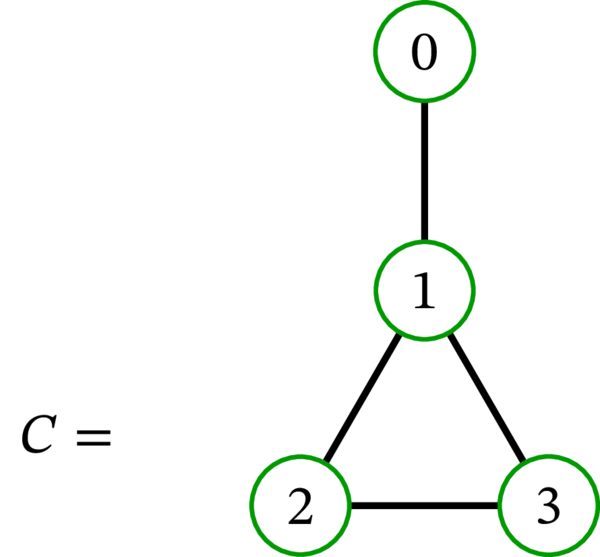
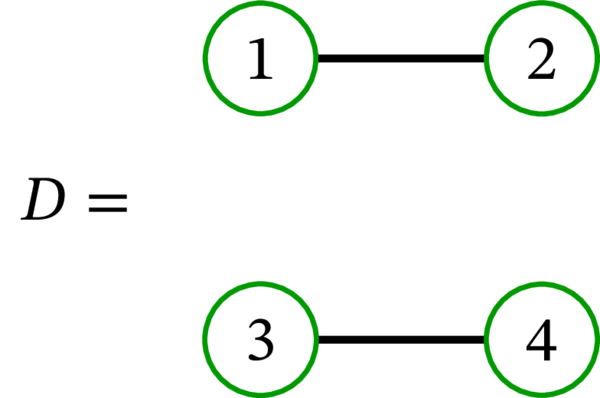
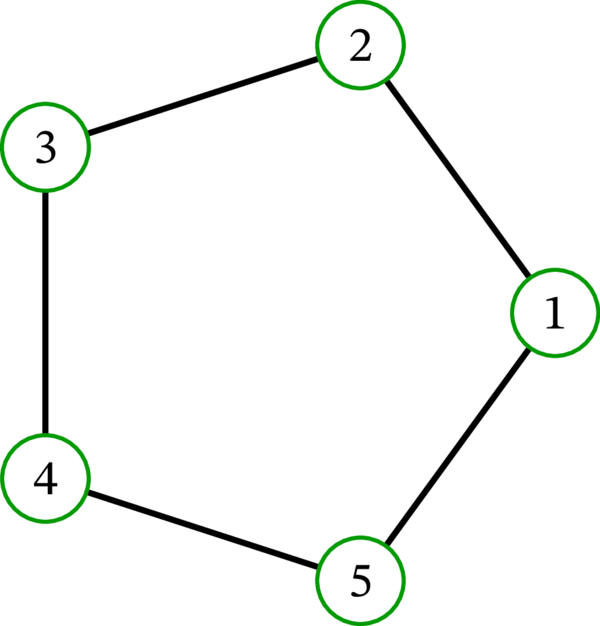
次のグラフの中でハミルトン路を持つのはどれか？ハミルトン閉路を持つのはどれか？

解答:

グラフ \(A\) はハミルトン閉路 \(\left( 1,2,3,4,5,6,1\right) \) とハミルトン路 \(\left( 1,2,3,4,5,6\right) \) を持つ。 [ハミルトン閉路を持つグラフは必ずハミルトン路も持つことを思い出してほしい。ハミルトン閉路の最後の頂点を除去すればハミルトン路が得られる。]
グラフ \(B\) はハミルトン路 \(\left( 2,3,1,4,5,6\right) \) を持ち、ハミルトン閉路を持たない。\(B\) がハミルトン閉路を持たない事実は次のように示せる: 辺 \(14\) は切断辺である (この辺を除去するとグラフが二つの成分に分かれる)。よって橋でもある (辺 \(14\) を含む閉路は \(B\) に存在しない)。つまり、\(B\) の任意の閉路は橋の「片側」にしか存在できない。
グラフ \(C\) はハミルトン路 \(\left( 0,1,2,3\right) \) を持ち、ハミルトン閉路を持たない。\(C\) がハミルトン閉路を持たないことは \(B\) と同様の議論で示せる (辺 \(01\) が橋である)。
グラフ \(D\) は連結でないので、ハミルトン路もハミルトン閉路も持たない。連結なグラフだけがハミルトン路を持つことができる。
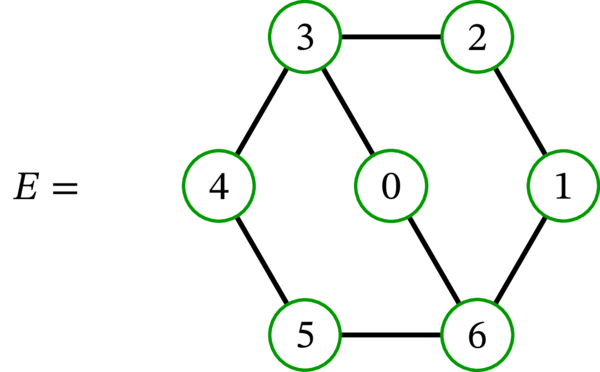
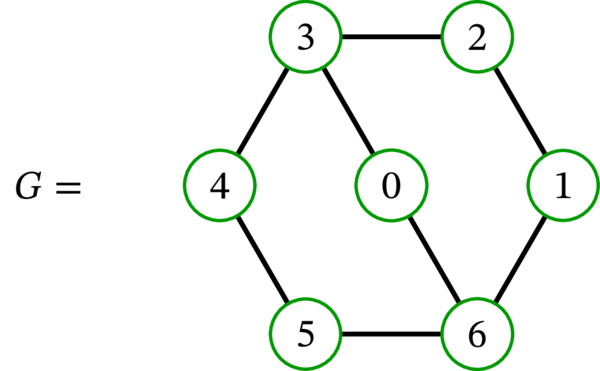
グラフ \(E\) はハミルトン路 \(\left( 0,3,2,1,6,5,4\right) \) を持ち、ハミルトン閉路を持たない (この事実の確認には多少手間がかかる)。
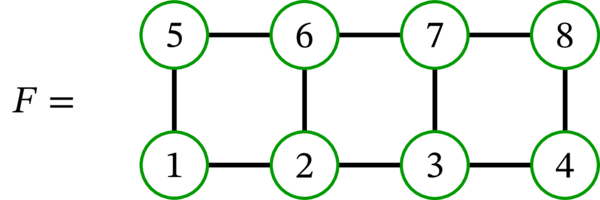
グラフ \(F\) はハミルトン閉路 \(\left( 1,2,3,4,8,7,6,5,1\right) \) を持ち、従ってハミルトン路も持つ。
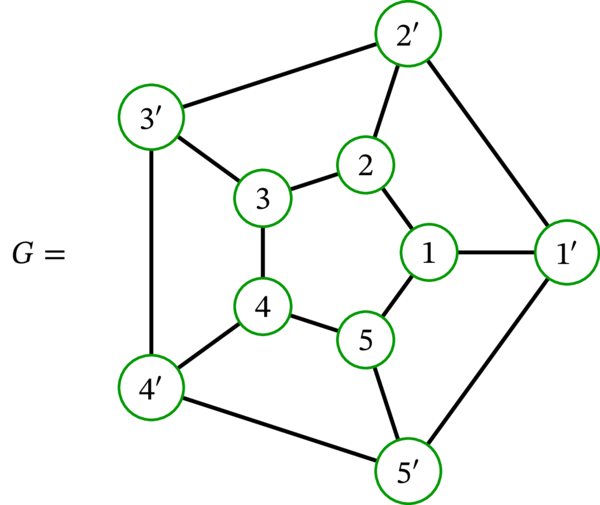
グラフ \(G\) はハミルトン閉路 \(\left( 1,2,3,4,5,5^{\prime},4^{\prime },3^{\prime},2^{\prime},1^{\prime},1\right) \) を持ち、従ってハミルトン路も持つ。
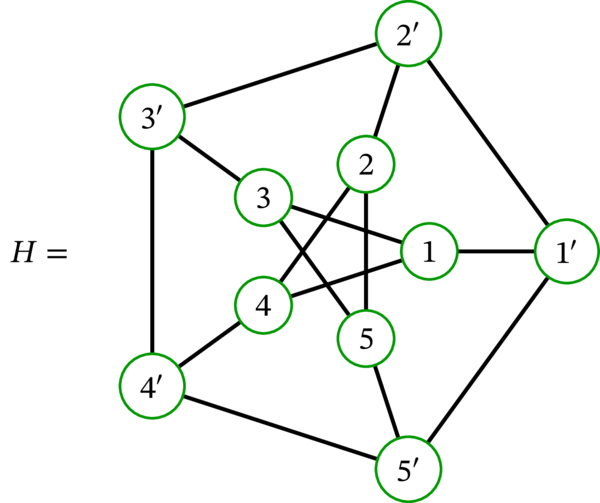
グラフ \(H\) (ところで、このグラフは第 2.6 3 項で触れた Petersen グラフである) はハミルトン路 \(\left( 1,3,5,2,4,4^{\prime},3^{\prime},2^{\prime},1^{\prime},5^{\prime}\right) \) を持ち、ハミルトン閉路を持たない。 [この事実は自明でない！ Wikipediaに解説がある。]

一般に、ハミルトン路またはハミルトン閉路を見つける (存在しないなら「存在しない」と答える) 問題は難易度が高い。「全ての頂点からなる列を列挙し、ハミルトン (閉) 路かどうかを一つずつ確認する」という総当たりを使えば必ず問題には答えられるものの、この方法はグラフが大きくなるとすぐに手に負えないほど長い時間がかかるようになる。総当たりより高速なアルゴリズム (具体的には、グラフの頂点数が \(n\) のとき実行時間が \(O\left( n^{2}2^{n}\right) \) のアルゴリズム) は存在するものの、多項式時間アルゴリズムは知られていない。ハミルトン路を見つける問題とハミルトン閉路を見つける問題は両方が NP 困難問題 (NP-hard problem) という区分に属する (これは計算複雑性理論の言葉である)。詳しくは Wikipedia を参照してほしい。

ハミルトン路を見つける問題はいわゆる巡回セールスマン問題 (traveling salesman problem, TSP) とも関連する。TSP は重み付きグラフの最小重みハミルトン路を見つける問題である (重み付きグラフでは全ての辺に「重み (weight)」と呼ばれる数値が関連付けられ、路の重みは含まれる辺の重みの和と定義される)。TSP はコンピューターサイエンス関係の様々な書籍で解説されている。

2.14.2十分条件: Ore と Dirac

これからハミルトン路とハミルトン閉路の存在に対する必要条件と十分条件をいくつか見ていく (どれも必要十分条件ではない)。次に示すのは最も有名な条件である:

定理 2.14.4

[Ore の定理 (Ore's theorem)] \(n\) 個の頂点を持つ単純グラフを \(G=\left( V,E\right) \) とする。ただし \(n \geq 3\) とする。

\(G\) で隣接しない任意の二頂点 \(x\), \(y\) で \(\deg x+\deg y\geq n\) が成り立つなら、\(G\) はハミルトン閉路を持つ。

この定理には様々な証明が知られている。例えば [Harju14, Theorem 3.6] や [Guicha16, Theorem 5.3.2] を参照してほしい。この二つと異なる証明を次に示す。これは Ore の定理を解説する Wikipedia ページの「アルゴリズム」節の内容に沿った証明である。

[定理 2.14.4 の証明] 集合 \(X\) の列挙 (listing) とは、\(X\) の要素を並べた列であって \(X\) の各要素をちょうど一度ずつ含むものを言う。明らかに、\(V\) の列挙は長さ \(n\) の列である。

列挙 \(\left( v_{1},v_{2},\ldots,v_{n}\right) \) の ハミルトン性 (hamness) を「\(v_{i}v_{i+1}\in E\) を満たす \(i\in\left\{ 1,2,\ldots,n\right\} \) の個数」として定義する。ただし \(v_{n+1} = v_{1}\) と解釈する。 [頂点 \(v_{1},v_{2},\ldots,v_{n}\) をこの順番で円周上に並べることで列挙 \(\left( v_{1},v_{2},\ldots,v_{n}\right) \) を描画したとき、隣り合う二つの頂点間にある \(G\) の辺の個数がその列挙のハミルトン性だと解釈できる。] 列挙 \(\left( v_{1},v_{2},\ldots,v_{n}\right) \) のハミルトン性は列挙を回転させても (例えば \(\left( v_{2},v_{3},\ldots,v_{n},v_{1}\right) \) にしても) 変化しないことに注意する。

まず、列挙 \(\left( v_{1},v_{2},\ldots,v_{n}\right) \) のハミルトン性が \(n\) 以上なら \(v_{1}v_{2},\ v_{2}v_{3},\ \ldots ,\ v_{n}v_{1}\) が全て \(G\) の辺なので、\(\left( v_{1},v_{2},\ldots ,v_{n},v_{1}\right) \) が \(G\) のハミルトン閉路となることは容易に分かる。よって、\(n\) 以上のハミルトン性を持つ \(V\) の列挙を見つければよい。

このために、ハミルトン性が \(n\) 未満の列挙からハミルトン性を大きくした列挙を作れることを示す。言い換えれば、次の命題を示す:

Claim 1: \(\left( v_{1},v_{2},\ldots,v_{n}\right) \) をハミルトン性が \(k < n\) の列挙とする。このとき、ハミルトン性が \(k\) より大きい列挙が存在する。

Claim 1 の証明: 列挙 \(\left( v_{1},v_{2},\ldots,v_{n}\right) \) のハミルトン性が \(k < n\) なので、\(v_{i}v_{i+1}\notin E\) を満たす \(i\in\left\{ 1,2,\ldots,n\right\} \) が存在する。そのような \(i\) に対して \(v_{i}\) と \(v_{i+1}\) は非隣接である。よって、定理の仮定から \(\deg v_{i} +\deg v_{i+1} \geq n\) を得る。

ここで、次の等式が成り立つ:

\[ \begin{aligned} \deg v_{i} & =\left\vert \left\{ w\in V\mid v_{i}w\in E\right\} \right\vert \\ & =\left\vert \left\{ j\in\left\{ 1,2,\ldots,n\right\} \mid v_{i}v_{j}\in E\right\} \right\vert \\ & =\left\vert \left\{ j\in\left\{ 1,2,\ldots,n\right\} \setminus\left\{ i\right\} \mid v_{i}v_{j}\in E\right\} \right\vert \\ & \qquad \qquad \left(\because\ j=i \text{ のとき } v_{i}v_{j} \notin E \right) \end{aligned} \]

また、次の等式も成り立つ:

\[ \begin{aligned} \deg v_{i+1} & =\left\vert \left\{ w\in V\mid v_{i+1}w\in E\right\} \right\vert \\ & =\left\vert \left\{ j\in\left\{ 1,2,\ldots,n\right\} \ \mid \ v_{i+1}v_{j+1}\in E\right\} \right\vert \\ & \qquad \qquad \left( \because\ v_{n+1} = v_{1} \right) \\ & =\left\vert \left\{ j\in\left\{ 1,2,\ldots,n\right\} \setminus\left\{ i\right\} \mid v_{i+1}v_{j+1}\in E\right\} \right\vert \\ & \qquad \qquad \left(\because\ j=i \text{ のとき } v_{i+1}v_{j+1} \notin E \right) \end{aligned} \]

この二つの等式を使って不等式 \(\deg v_{i} +\deg v_{i+1} \geq n\) を変形すると、次を得る:

\[ \begin{aligned} & \left\vert \left\{ j\in\left\{ 1,2,\ldots,n\right\} \setminus\left\{ i\right\} \mid v_{i}v_{j}\in E\right\} \right\vert \\ & \ \ \ \ \ \ \ \ \ \ +\left\vert \left\{ j\in\left\{ 1,2,\ldots,n\right\} \setminus\left\{ i\right\} \mid v_{i+1}v_{j+1}\in E\right\} \right\vert \geq n \end{aligned} \]

つまり、\(\left\{ j\in\left\{ 1,2,\ldots,n\right\} \setminus\left\{ i\right\} \mid v_{i}v_{j}\in E\right\} \) と \(\left\{ j\in\left\{ 1,2,\ldots,n\right\} \setminus\left\{ i\right\} \mid v_{i+1}v_{j+1}\in E\right\} \) の大きさの和は \(n\) 以上である。この二つの集合はどちらも \(n-1\) 要素集合 \(\left\{ 1,2,\ldots,n\right\} \setminus\left\{ i\right\} \) の部分集合だから、二つの集合には共通要素が存在する。言い換えれば、\(v_{i}v_{j}\in E\) と \(v_{i+1}v_{j+1}\in E\) を満たす \(j\in\left\{ 1,2,\ldots,n\right\} \setminus\left\{ i\right\} \) が存在する。そのような \(j\) を固定する。

続いて、元々の列挙 \(\left( v_{1},v_{2},\ldots,v_{n}\right) \) から次の操作で新しい列挙を作成する:

まず、元々の列挙を回転して \(v_{i+1}\) から始まるようにする。この操作によって列挙 \(\left( v_{i+1},v_{i+2},\ldots ,v_{n},v_{1},v_{2},\ldots,v_{i}\right) \) が得られる。
次に、この列挙の先頭 \(v_{i+1}\) から \(v_{j}\) までの部分を反転する。この操作によって次の列挙が得られる:

\[ \left( \underbrace{v_{j},v_{j-1},\ldots,v_{i+1}}_{\substack{ \text{反転した部分}\\ \ldots,v_{1},v_{n},\ldots \text{ を含む場合もあれば} \\ \text{含まない場合もある} \\ }}, \underbrace{v_{j+1},v_{j+2},\ldots,v_{i}}_ {\substack{\text{反転していない部分}}}\right) \]

この新しい列挙が \(k\) より大きいハミルトン性を持つと示す。列挙の回転ではハミルトン性は変化しないのに対して、\(v_{i+1}\) から \(v_{j}\) までの部分を反転させる操作では明らかにハミルトン性が変化する。反転後の列挙では \(v_{i}v_{i+1}\) と \(v_{j}v_{j+1}\) の二辺がハミルトン性に寄与しなくなり、\(v_{i}v_{j}\) と \(v_{i+1}v_{j+1}\) の二辺が新たに寄与するようになる。この取り引きは得である: 追加される辺 \(v_{i}v_{j}\), \(v_{i+1}v_{j+1}\) (\(j\) の定義より両方とも存在する) によってハミルトン性は \(2\) だけ増え、除去される辺によってハミルトン性は \(0\) または \(1\) だけ減る (\(i\) の定義より辺 \(v_{i}v_{i+1}\) は存在しない)。よって、新しい列挙のハミルトン性は元々の列挙より \(1\) または \(2\) だけ増加する。言い換えれば、新しい列挙のハミルトン性は \(m\) より \(1\) または \(2\) だけ大きい。以上で Claim 1 は証明された。

よって、Claim 1 を使って 任意の列挙 \(V\) を改変し続ければ、改変のたびにハミルトン性が増加し、いずれは \(n\) 以上となる。上述したようにハミルトン性が \(n\) 以上の列挙はハミルトン閉路だから、以上で定理 2.14.4 は証明された。□

系 2.14.5

[Dirac の定理 (Dirac's theorem)] \(n\) 個の頂点を持つ単純グラフを \(G=\left( V,E\right) \) とする。ただし \(n \geq 3\) とする。

任意の頂点 \(x \in V\) で \(\deg x\geq\dfrac{n}{2}\) が成り立つなら、\(G\) はハミルトン閉路を持つ。

[証明] \(G\) の任意の二頂点 \(x\), \(y\) が

\[ \underbrace{\deg x}_{\geq\dfrac{n}{2}}+\underbrace{\deg y}_{\geq\dfrac{n}{2}}\geq\dfrac{n}{2}+\dfrac{n}{2}=n \]

を満たすので、Ore の定理から従う。□

練習問題 2.22

\(G=\left( V,E\right) \) を単純グラフ、\(u\) と \(v\) を \(G\) の相異なる非隣接な二頂点、\(n=\left\vert V\right\vert \) とする。\(\deg u+\deg v\geq n\) が成り立ち、\(G\) に辺 \(uv\) を加えたグラフ \(G^{\prime}=\left( V,E\cup\left\{ uv\right\} \right) \) がハミルトン閉路を持つという。\(G\) もハミルトン閉路を持つと示せ。
前問の「ハミルトン閉路」を「ハミルトン路」に置き換えた命題は成り立つか？

2.14.3必要条件

十分条件はこれくらいにしておこう。必要条件はどうだろうか？

命題 2.14.6

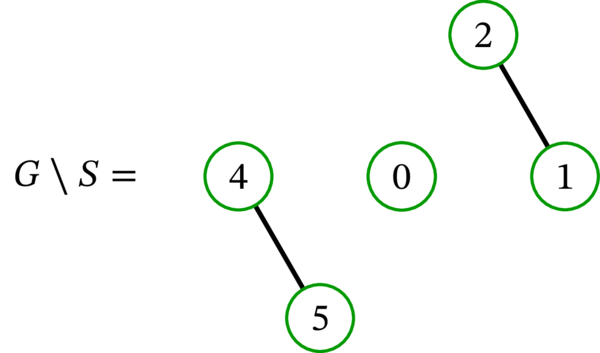
\(G=\left( V,E\right) \) を単純グラフとする。\(V\) の任意の部分集合 \(S\) に対して、集合 \(V\setminus S\) に関する \(G\) の誘導部分グラフを \(G\setminus S\) と表す。 [言い換えれば、\(G\setminus S\) は \(G\) から \(S\) に属する頂点と端点のいずれかが \(S\) に属する辺を除いたグラフである。]

[単純グラフ \(G\) と \(G\setminus S\) の例を示す:

ここで \(S=\left\{ 3,6\right\} \) である。]

また、単純グラフ \(H\) の連結成分の個数を \(b_{0}\left( H\right) \) と表す。

\(G\) がハミルトン閉路を持つなら、空でない任意の \(S\subseteq V\) に対して \(b_{0}\left( G\setminus S\right) \leq\left\vert S\right\vert \) が成り立つ。
\(G\) がハミルトン路を持つなら、任意の \(S\subseteq V\) に対して \(b_{0}\left( G\setminus S\right) \leq\left\vert S\right\vert +1\) が成り立つ。

例えば、例 2.14.3 の \(E\) で \(S\) を \(\left\{ 3,6\right\} \) とすると \(b_{0}\left( G\setminus S\right) =3\) かつ \(\left\vert S\right\vert =2\) なので、命題 2.14.6 (a) より \(E\) はハミルトン閉路を持たないと分かる。このように、命題 2.14.6 はハミルトン閉路とハミルトン路が存在しないことを示すのに利用できる。

[命題 2.14.6 の証明] (a): \(S \subseteq V\) を非空集合とする。閉路から \(\left\vert S\right\vert \) 個の頂点を取り除くと、閉路は最大で \(\left\vert S\right\vert \) 個の路に分かれる:

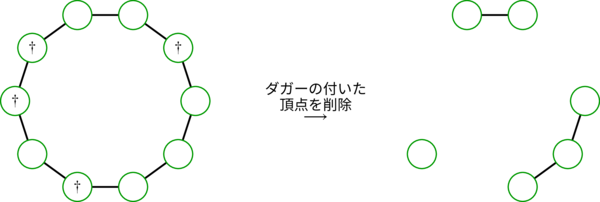
もちろん今考えているグラフ \(G\) は一般に閉路グラフではないものの、\(G\) はハミルトン閉路を持つ。\(S\) に属する頂点を取り除くと、そのハミルトン閉路は最大で \(\left\vert S\right\vert \) 個の路に分かれる。よってグラフ \(G\setminus S\) の成分の個数は最大でも (\(G\) でハミルトン閉路に属していた辺だけを考える場合でも) \(\left\vert S\right\vert \) だと分かる。他の辺を考えに入れたとしても成分の個数は増えないので、(a) は証明された。

(b): (a) と同様に証明できる。□

この命題を使うとグラフがハミルトン路またはハミルトン閉路を持たない事実を示せることが多い。しかし、この命題の逆は成り立たないので、万能ではない。実際、第 2.6.3 項で定義した Petersen グラフはハミルトン閉路を持たないものの、命題 2.14.6 (a) の条件「空でない任意の \(S \subseteq V\) に対して \(b_{0}\left( G\setminus S\right) \leq\left\vert S\right\vert \)」を満たす。

2.14.4超立方体

続いて、ハミルトン閉路を持つグラフの具体的な例を見ていこう。

定義 2.14.7

\(n \in \mathbb{N}\) に対して、\(n\) 次元超立方体グラフ (\(n\)-th hypercube graph) \(Q_{n}\) を次のように定義する。まず、\(Q_{n}\) の頂点集合は次の集合である:

\[ \left\{ 0,1\right\} ^{n}=\left\{ \left( a_{1},a_{2},\ldots,a_{n}\right) \mid a_{i} \in \left\{ 0,1\right\}\ \wedge\ i \in \left\{1,2,\dots,n\right\} \right\} \]

次に、\(Q_{n}\) の辺は次のように定義される: 異なる二つの頂点 \(\left( a_{1},a_{2},\ldots ,a_{n}\right) \in\left\{ 0,1\right\} ^{n}\) と \(\left( b_{1},b_{2},\ldots,b_{n}\right) \in\left\{ 0,1\right\} ^{n}\) は、\(a_{i}\neq b_{i}\) を満たす \(i\in\left\{ 1,2,\ldots,n\right\} \) がちょうど一つ存在するとき、かつそのときに限って隣接する。 [例えば \(Q_{4}\) では頂点 \(\left( 0,1,1,0\right) \) と頂点 \(\left( 0,1,0,0\right) \) が隣接する。] なお、本書では \(n\) 次元超立方体グラフを単に「\(n\) 次元超立方体」とも呼ぶ。

\(\left\{ 0,1\right\} ^{n}\) の要素はビット文字列 (bitstring) あるいは二進単語 (binary word) と呼ばれ、ビット文字列の各要素はビット (bit) あるいは文字 (letter) と呼ばれることが多い。この言葉を使えば、\(Q_{n}\) において二つのビット文字列はちょうど一つのビットが異なるとき、かつそのときに限って隣接する。

本書ではビット文字列 \(\left( a_{1},a_{2},\ldots,a_{n}\right) \) を \(a_{1}a_{2}\cdots a_{n}\) と省略して書く場合がある。例えば \(\left( 0,1,1,0\right) \) を \(0110\) と書く。

例 2.14.8

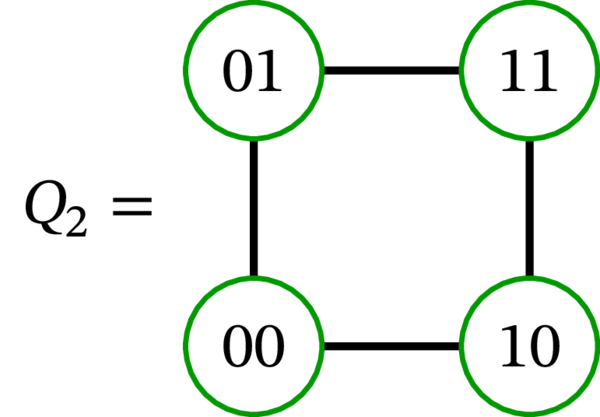
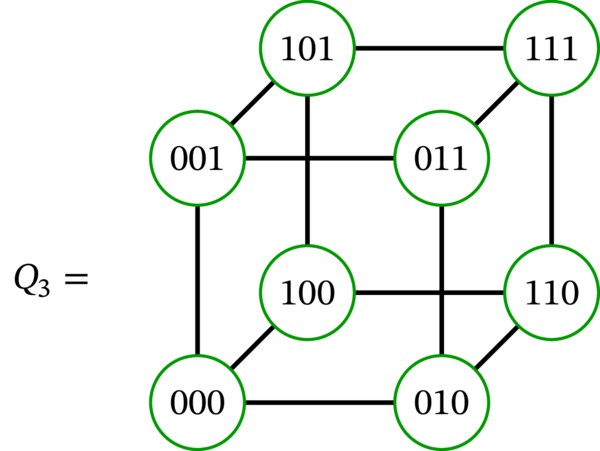
\(n=1,2,3\) に対する \(n\) 次元超立方体 \(Q_{n}\) を示す:

これを見れば「超立方体」と言う名前の意味が理解できるだろう。なお、\(0\) 次元超立方体 \(Q_{0}\) は空のビット文字列 \(\left( {}\right) \) を唯一の頂点とするグラフである。

定理 2.14.9

[Gray] \(n \geq 2\) のとき \(Q_{n}\) はハミルトン閉路を持つ。

\(Q_{n}\) のハミルトン閉路はグレイ符号 (Gray code) という名前で知られる。つまり、グレイ符号は長さ \(n\) の全ビット文字列からなる \(2^{n}\) 要素の環状リストであって、隣り合うビット文字列が必ず \(1\) ビットだけ異なるという性質を持つ。グレイ符号の応用は Wikipedia で解説されている。

[定理 2.14.9 の証明] 示すべき命題よりも強い次の命題を証明する:

Claim 1: 任意の \(n\geq 1\) に対して、\(n\) 次元超立方体 \(Q_{n}\) は \(00\cdots0\) から \(100\cdots0\) へのハミルトン路を持つ。

[\(00\cdots0\) と \(100\cdots0\) が表すのはビット文字列であって数字ではないことに注意してほしい。つまり

\[ 00\cdots0 = \left( \underbrace{0,0,\ldots,0}_{0 \text{ が } n \text{ 個}}\right), \quad 100\cdots0 = \left( 1,\underbrace{0,0,\ldots,0}_{0 \text{ が } n-1 \text{ 個}}\right) \]

が成り立つ。]

[Claim 1 の証明: \(n\) に関する数学的帰納法で示す。

ベースケース: \(Q_{1}\) に \(0\) から \(1\) へのハミルトン路が存在することは明らかである。

帰納ステップ: \(N \geq 2\) を固定する。Claim 1 が \(n = N - 1\) の場合に成り立つと仮定する。この仮定より、\(Q_{N-1}\) には \(\underbrace{00\cdots 0}_{N-1\text{ 個}}\) から \(1\underbrace{00\cdots0}_{N-2\text{ 個}}\) へのハミルトン路が存在する。そのようなハミルトン路を一つ取って \(\mathbf{p}\) とする。

\(\mathbf{p}\) に含まれる各ビット文字列 (頂点) の先頭に \(0\) を付けると、\(Q_{N}\) における \(\underbrace{00\cdots0}_{N\text{ 個}}\) から \(01\underbrace{00\cdots0}_{N-2\text{ 個}}\) への路 \(\mathbf{q}\) が得られる。

同様に、\(\mathbf{p}\) に含まれる各ビット文字列 (頂点) の先頭に \(1\) を付けると、\(Q_{N}\) における \(1\underbrace{00\cdots0}_{N-1\text{ 個}}\) から \(11\underbrace{00\cdots0}_{N-2\text{ 個}}\) への路 \(\mathbf{r}\) が得られる。

次に、\(Q_{N}\) における \(\underbrace{00\cdots0}_{N\text{ 個}}\) から \(1\underbrace{00\cdots0}_{N-1\text{ 個}}\) へのハミルトン路を次のように構成する:

\(\underbrace{00\cdots0}_{N\text{ 個}}\) を出発して、路 \(\mathbf{q}\) の頂点を最後まで (\(01\underbrace{00\cdots0}_{N-2\text{ 個}}\) まで) たどる。
隣接頂点 \(11\underbrace{00\cdots0}_{N-2\text{ 個}}\) に移動する。
路 \(\mathbf{r}\) の頂点を逆順にたどる。最終的に \(1\underbrace{00\cdots0}_{N-1\text{ 個}}\) に到着する。

この路は条件を満たすハミルトン路なので、Claim 1 は \(n=N\) の場合でも成り立つ。以上で Claim 1 は証明された。]

Claim 1 からは、\(n\) 次元超立方体 \(Q_{n}\) が \(00\cdots0\) から \(100\cdots0\) へのハミルトン路を持つことが分かる。このハミルトン路の始点 \(00\cdots0\) と終点 \(100\cdots0\) は隣接するから、始点 \(00\cdots0\) を末尾に追加することでハミルトン閉路を構築できる。以上で定理 2.14.9 は証明された。□

2.14.5デカルト積

実は定理 2.14.9 には一般化が存在する。その一般化を表明するために、二つのグラフのデカルト積を定義する:

定義 2.14.10

\(G=\left( V,E\right) \) と \(H=\left( W,F\right) \) を二つの単純グラフとする。\(G\) と \(H\) のデカルト積 (Cartesian product) \(G\times H\) とは、次の \(E^{\prime }\), \(F^{\prime}\) を使って定義される単純グラフ \(\left( V\times W,\ E^{\prime }\cup F^{\prime}\right) \) を言う:

\[ \begin{aligned} E^{\prime} & \colonequals \left\{ \left( v_{1},w\right) \left( v_{2},w\right) \mid v_{1}v_{2}\in E \ \wedge\ w\in W\right\} \\ F^{\prime} & \colonequals \left\{ \left( v,w_{1}\right) \left( v,w_{2}\right) \mid w_{1}w_{2}\in F \ \wedge\ v\in V\right\} \end{aligned} \]

言い換えれば、デカルト積 \(G \times H\) の頂点集合は \(G\) の頂点と \(H\) の頂点の組 \(\left( v,w\right) \in V\times W\) から構成され、辺集合は次の二つの形をした頂点の二要素集合から構成される:

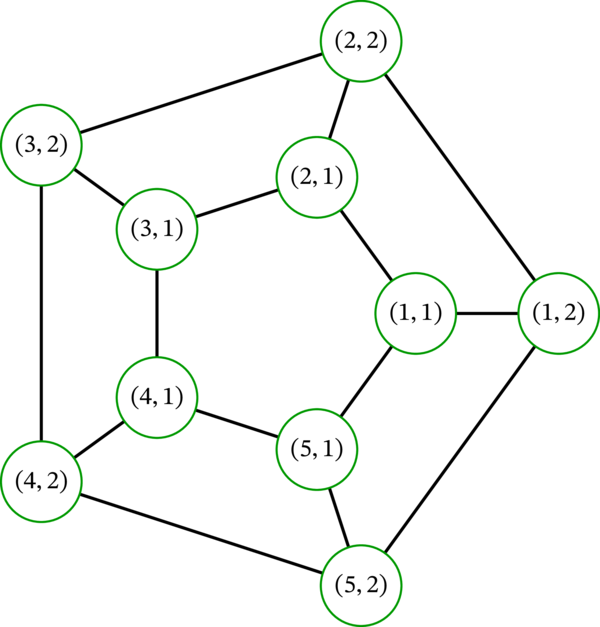
\[ \begin{aligned} \left( v_{1},w\right) \left( v_{2},w\right) \qquad v_{1}v_{2} \in E,\ w\in W \\ \left( v,w_{1}\right) \left( v,w_{2}\right) \qquad w_{1}w_{2}\in F,\ v\in V \end{aligned} \]

例えば、任意のグラフ \(G\) と \(2\) 次の路グラフ \(P_{2}\) とデカルト積 \(G \times P_{2}\) の描画は、\(G\) の描画を二つ少しずらして書き、二つの \(G\) の描画で同じ頂点を表す点を曲線で結ぶと得られる。このとき一方の \(G\) の描画に含まれるのが \(\left(v, 1\right)\) の形をした \(G \times P_{2}\) の頂点であり、もう一方の \(G\) の描画に含まれるのが \(\left(v, 2\right)\) の形をした \(G \times P_{2}\) の頂点である。具体的な例として、\(5\) 次の閉路グラフ \(C_{5}\) とデカルト積 \(C_{5}\times P_{2}\) の描画を次に示す:

前段落の \(G \times P_{2}\) の説明が理解できれば、次の命題は容易に分かる:

命題 2.14.11

\(n \geq 1\) なら \(Q_{n}\cong Q_{n-1}\times P_{2}\) が成り立つ。 [\(Q_{n}\) と \(Q_{n-1}\) は定義 2.14.7 で定めた。]

[証明] これは 2017 年春学期に開講された講義で出した homework set #2 の Exercise 1 (a) である。解答は講義ページに載っている。□

さらに、次の命題が成り立つ:

定理 2.14.12

\(G\) と \(H\) を単純グラフとする。\(G\) と \(H\) がハミルトン路を持つとき:

デカルト積 \(G \times H\) はハミルトン路を持つ。
\(\left\vert \operatorname*{V}\left( G\right) \right\vert \) と \(\left\vert \operatorname*{V}\left( H\right) \right\vert \) が両方とも \(1\) より大きい偶数なら、デカルト積 \(G \times H\) はハミルトン閉路を持つ。

[証明] これは 2017 年春学期に開講された講義で出した homework set #2 の Exercise 1 (b), (c) である。解答は講義ページに載っている。□

\(P_{2}\) はハミルトン路を持ち、\(\left\vert \operatorname*{V}\left( P_{2}\right) \right\vert =2\) は偶数なので、定理 2.14.12 (b) を使うと定理 2.14.9 の別証明が得られる (ここでも \(n\) に関する帰納法を使う)。 [確かに証明できることを納得せよ！]

2.14.6部分集合グラフ

\(n\) 次元超立方体 \(Q_{n}\) は \(\left\{ 1,2,\ldots,n\right\} \) の部分集合を使って解釈することもできる。\(n \in \mathbb{N}\) に対して、単純グラフ \(G_{n}\) を次のように定義する。\(G_{n}\) の頂点集合は \(\left\{ 1,2,\ldots,n\right\} \) の冪集合 \(\mathcal{P}\left( \left\{ 1,2,\ldots,n\right\} \right) \) (つまり、\(\left\{ 1,2,\ldots ,n\right\} \) の \(2^{n}\) 個ある部分集合が全て頂点) であり、辺は次のように定める: 二つの頂点 \(S\), \(T\) は「\(S\) と \(T\) のいずれかが、もう一方に要素を一つ追加することで得られる」とき (「ある \(s \notin T\) に対して \(S=T\cup\left\{ s\right\} \)」または「ある \(t \notin S\) に対して \(T=S\cup\left\{ t\right\} \)」が成り立つとき)、かつそのときに限って隣接する。このとき \(G_{n}\cong Q_{n}\) が成り立つ。実際、次の写像が \(Q_{n}\) から \(G_{n}\) へのグラフ同型写像となる:

\[ \begin{aligned} \left\{ 0,1\right\} ^{n} & \rightarrow\mathcal{P}\left( \left\{ 1,2,\ldots,n\right\} \right) \\ \left( a_{1},a_{2},\ldots,a_{n}\right) & \mapsto\left\{ i\in\left\{ 1,2,\ldots,n\right\} \mid a_{i}=1\right\} \end{aligned} \]

よって定理 2.14.9 からは任意の \(n \geq 2\) に対して \(G_{n}\) がハミルトン閉路を持つと分かる。言い換えれば、\(n \geq 2\) なら \(\left\{ 1,2,\ldots,n\right\} \) の部分集合を環状に並べて、任意の部分集合に要素を一つ追加または除去すると「次の」部分集合が得られるようにできる。例えば、条件を満たすように \(\left\{ 1,2,3 \right\} \) の部分集合を並べると次のようになる:

\[ \varnothing,\ \ \left\{ 1\right\} ,\ \ \left\{ 1,2\right\} ,\ \ \left\{ 2\right\} ,\ \ \left\{ 2,3\right\} ,\ \ \left\{ 1,2,3\right\} ,\ \ \left\{ 1,3\right\} ,\ \ \left\{ 3\right\} \]

「\(n\) が奇数のとき、\(\left\{ 1,2,\ldots,n\right\} \) の \(\dfrac{n\pm1}{2}\) 要素部分集合を同じように並べられるか？」という問題は長く未解決だったものの、つい数年前に解決された。例えば、\(n=3\) のときは次のように部分集合を並べられる:

\[ \left\{ 1\right\} ,\ \ \left\{ 1,2\right\} ,\ \ \left\{ 2\right\} ,\ \ \left\{ 2,3\right\} ,\ \ \left\{ 3\right\} ,\ \ \left\{ 1,3\right\} \]

\(G_{n}\cong Q_{n}\) なので、この問題は次のように言い換えられる: \(n\) を \(3\) 以上の奇数とするとき、次の集合に関する \(Q_{n}\) の誘導部分グラフを \(Q_{n}^{\prime}\) とする:

\[ \left\{ a_{1}a_{2}\cdots a_{n}\in\left\{ 0,1\right\} ^{n}\mid \sum _{i=1}^{n}a_{i}\in\left\{ \dfrac{n-1}{2},\dfrac{n+1}{2}\right\} \right\} \]

\(Q_{n}^{\prime}\) はハミルトン閉路を持つか？

2014 年、この問題の答えが「Yes」であることが Torsten Mütze によって証明された。彼の真に非自明な証明は [Mutze14] から確認できる。また、[Mutze22] は同様の問題に関するサーベイである (こちらも参照: change ringing)。

次の練習問題では定理 2.14.9 の異なる一般化を証明する:

練習問題 2.23

\(n\) と \(k\) を \(n > k > 0\) を満たす二つの整数とする。単純グラフ \(Q_{n,k}\) を次のように定める: \(Q_{n,k}\) の頂点はビット文字列 \(\left( a_{1},a_{2},\ldots,a_{n}\right) \in\left\{ 0,1\right\} ^{n}\) であり、二つのビット文字列はちょうど \(k\) ビットが異なるとき、かつそのときに限って隣接する。言い換えれば、頂点 \(\left( a_{1},a_{2},\ldots,a_{n}\right) \) と頂点 \(\left( b_{1},b_{2},\ldots,b_{n}\right) \) は \(a_{i}\neq b_{i}\) を満たす \(i\in\left\{ 1,2,\ldots,n\right\} \) の個数がちょうど \(k\) に等しいとき、かつそのときに限って隣接する。 [例えば \(Q_{n,1}\) は \(n\) 次元超立方体グラフ \(Q_{n}\) である。]

\(k\) が偶数のとき \(Q_{n,k}\) はハミルトン閉路を持つか？
\(k\) が奇数のとき \(Q_{n,k}\) はハミルトン閉路を持つか？

[ヒント: (b) では、集合 \(\left\{ 0, 1 \right\} \) を二要素の有限体 \(\mathbb{F}_{2}\) とみなすアプローチが利用できる。このときビット文字列 \(\left( a_{1}, a_{2}, \ldots, a_{n} \right) \in\left\{ 0, 1 \right\} ^{n}\) は \(\mathbb{F}_{2}\) 上のベクトル空間 \(\mathbb{F}_{2}^{n}\) における大きさ \(n\) のベクトルとなる。\(e_{1}, e_{2}, \ldots, e_{n}\) を \(\mathbb{F}_{2}^{n}\) の標準基底ベクトルとする (つまり \(e_{i}\) は第 \(i\) 要素に \(1\) を持ち、他の要素は全て \(0\) である)。すると、\(n\) 次元超立方体グラフ \(Q_{n}\) において二つのベクトルは両者の差が標準基底ベクトルのいずれかに等しいとき、かつそのときに限って隣接する。\(Q_{n,k}\) についても (「標準基底ベクトル」を「\(k\) 個の標準基底ベクトルの和」と置き換えれば) 同様のことが言える。この事実を使うと、\(Q_{n}\) から \(Q_{n,k}\) の部分グラフへのグラフ同型写像を示せる。]

次の練習問題では定理 2.14.9 の証明で使ったアイデアを拡張して用いる:

練習問題 2.24

\(n \geq 1\) を整数、定義 2.14.7 で定めた \(n\) 次元超立方体グラフを \(Q_{n}\) とする。

頂点 \(00\cdots0\) から始まる \(Q_{n}\) のハミルトン路の終点として可能な頂点を全て求めよ。解答した頂点で終わるハミルトン路が存在すること、それら以外の頂点で終わるハミルトン路が存在しないことをそれぞれ示すこと。