2.3. 最初の事実: ラムゼー数 \(R(3,3) = 6\)
定義はもう十分だろう。続いて本書で最初の命題を証明する:
\(G\) は単純グラフで \(\left| \operatorname{V}\left( G \right) \right| \geq6\) を満たすとする (つまり、\(G\) は \(6\) 個以上の頂点を持つとする)。このとき、次の二つの命題の少なくとも一方が成り立つ:
-
命題 1: 辺 \(ab\), \(bc\), \(ca\) が全て \(G\) に存在するような \(G\) の頂点 \(a\), \(b\), \(c\) が存在する。
-
命題 2: 辺 \(ab\), \(bc\), \(ca\) がいずれも \(G\) に存在しないような \(G\) の頂点 \(a\), \(b\), \(c\) が存在する。
言い換えれば、命題 2.3.1 は「\(G\) が少なくとも \(6\) 個の頂点を持つなら、相互に隣接する三頂点1または相互に非隣接な (どの二頂点も隣接していない) 三頂点 (あるいはその両方) を見つけられる」と主張している。この命題は「六人以上が集まると、知り合い同士の三人組または初対面同士の三人組 (あるいはその両方) を必ず見つけられる」とも言い換えられる。ここでは初対面でない人は知り合いだと仮定されている。
この命題の具体例は後で示す。まずは議論で便利な用語を定義する:
\(G\) を単純グラフとする。
-
\(G\) の三頂点 \(a\), \(b\), \(c\) のどの二つも隣接する (つまり、\(ab\), \(bc\), \(ca\) が全て \(G\) の辺である) なら、集合 \(\left\{ a,b,c\right\} \) を \(G\) の三角形 (triangle) と呼ぶ。
-
\(G\) の三頂点 \(a\), \(b\), \(c\) のどの二つも隣接しない (つまり、\(ab\), \(bc\), \(ca\) がいずれも \(G\) の辺でない) なら、集合 \(\left\{ a,b,c\right\} \) を \(G\) の反三角形 (anti-triangle) と呼ぶ。
この用語を使うと、命題 2.3.1 は「\(6\) 個以上の頂点を持つ任意の単純グラフは三角形または半三角形 (あるいはその両方) を持つ」と言い換えられる。
命題 2.3.1 が適用できるグラフの例を二つ、そして適用できないグラフの例を一つ示す。
-
\(V\) と \(E\) を次のように定め、グラフ \(G = \left(V, E\right)\) を定義する:
\[ \begin{aligned} V & =\left\{ 1,2,3,4,5,6\right\} \\ E & =\left\{ \left\{ 1,2\right\} ,\left\{ 2,3\right\} ,\left\{ 3,4\right\} ,\left\{ 4,5\right\} ,\left\{ 5,6\right\} ,\left\{ 6,1\right\} \right\} \end{aligned} \]\(G\) は正六角形の形に描画できる:
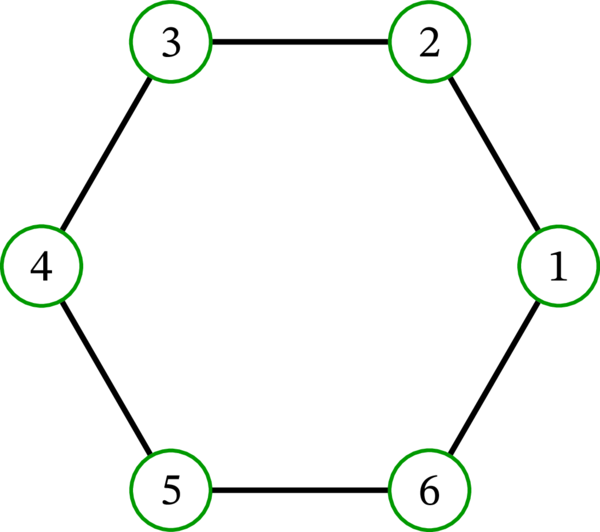
\(G\) は命題 2.3.1 の仮定を満たす。実際、\(\left\{ 1,3,5\right\} \) や \(\left\{ 2,4,6\right\} \) は \(G\) の反三角形である。
-
\(V\) と \(E\) を次のように定め、グラフ \(G = \left(V, E\right)\) を定義する:
\[ \begin{aligned} V & =\left\{ 1,2,3,4,5,6\right\} \\ E & =\left\{ \left\{ 1,2\right\} ,\left\{ 2,3\right\} ,\left\{ 3,4\right\} ,\left\{ 4,5\right\} ,\left\{ 5,6\right\} ,\left\{ 6,1\right\} ,\left\{ 1,3\right\} ,\left\{ 4,6\right\} \right\} \end{aligned} \]\(G\) は正六角形に二本の対角線を引いた形に描画できる:
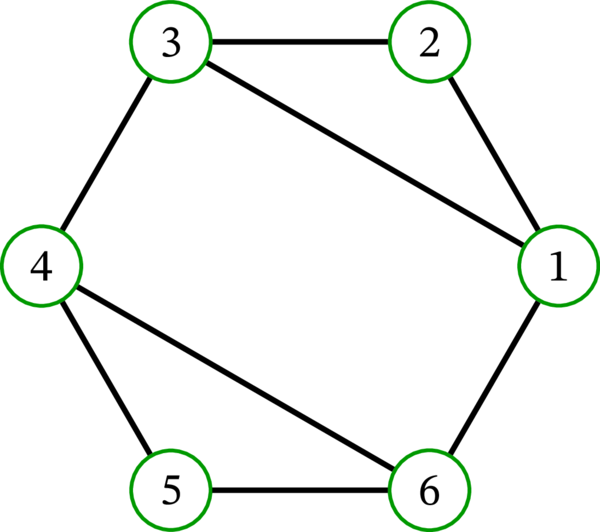
\(G\) は命題 2.3.1 の仮定を満たす。実際、\(\left\{ 1,2,3\right\} \) と \(\left\{ 4,5,6\right\} \) は \(G\) の三角形である。
-
\(V\) と \(E\) を次のように定め、グラフ \(G = \left(V, E\right)\) を定義する:
\[ \begin{aligned} V & =\left\{ 1,2,3,4,5\right\} \\ E & =\left\{ \left\{ 1,2\right\} ,\left\{ 2,3\right\} ,\left\{ 3,4\right\} ,\left\{ 4,5\right\} ,\left\{ 5,1\right\} \right\} \end{aligned} \]\(G\) は正五角形の形に描画できる:
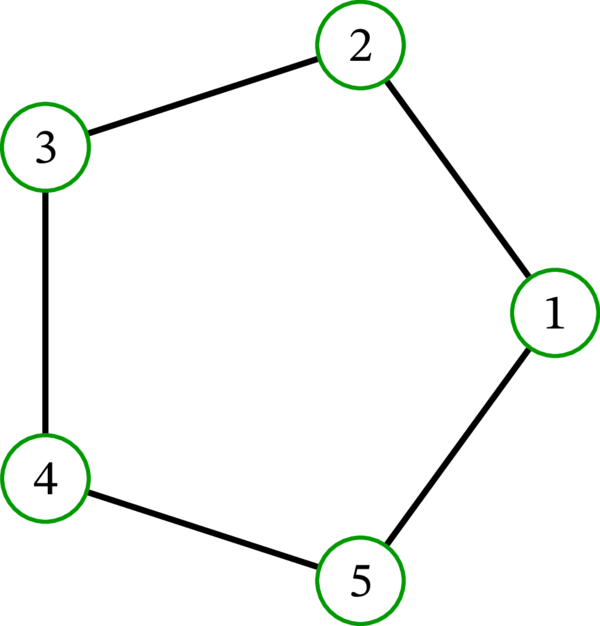
\(G\) は命題 2.3.1 の仮定 \(\left\vert \operatorname{V}\left( G\right) \right\vert \geq 6\) を満たさないので、命題 2.3.1 は \(G\) に関して何も言わない。そのため、命題 2.3.1 の結論が \(G\) に対して正しいかどうかはすぐには分からない。しかし、結論が偽であることは簡単に確かめられる: \(G\) は三角形も反三角形も持たない。
\(G\) が三角形または反三角形 (もしくはその両方) を持つと示す必要がある。
頂点 \(u\in\operatorname{V}\left( G\right) \) を任意に取る (\(\left\vert \operatorname{V}\left( G\right) \right\vert \geq6\geq1\) なので、この操作は明らかに行える)。このとき、\(G\) は少なくとも \(6\) 個の頂点を持つことから、\(u\) 以外に \(G\) の頂点が少なくとも \(5\) 個存在する。続いて、二つの場合を分けて考える:
- Case 1: 頂点 \(u\) が \(3\) 個以上の隣接頂点を持つ。
- Case 2: 頂点 \(u\) が \(2\) 個以下の隣接頂点しか持たない。
まず Case 1 を考える。\(u\) は \(3\) 個以上の隣接頂点を持つので、相異なる \(u\) の隣接頂点 \(p\), \(q\), \(r\) を見つけることができる。もし \(pq\), \(qr\), \(rp\) のいずれかが \(G\) の辺なら、\(G\) は三角形を持つ (例えば、もし \(pq\) が \(G\) の辺なら \(\left\{ u,p,q\right\} \) が三角形となる)。そうでないなら、\(G\) は反三角形 \(\left\{ p,q,r\right\} \) を持つ。よって Case 1 で命題は証明された。
続いて Case 2 を考える。\(u\) の隣接頂点は \(2\) 個以下で \(G\) の頂点数は \(6\) 個以上なので、\(u\) は少なくとも \(3\) 個の非隣接頂点を持つ2。よって、相異なる \(u\) の非隣接頂点 \(p\), \(q\), \(r\) を見つけることができる。もし \(pq\), \(qr\), \(rp\) が全て \(G\) の辺なら、\(G\) は三角形 \(\left\{ p,q,r\right\} \) を持つ。もしそうでないなら、\(G\) は反三角形を持つ (例えば、\(pq\) が \(G\) の辺でないなら \(\left\{ u,p,q\right\} \) が反三角形となる)。よって Case 2 で命題は証明された。
Case 1 と Case 2 の両方で命題が証明できたので、命題 2.3.1 は証明された。□
Case 1 の証明と Case 2 の証明が似ている点に注目してほしい。「隣接頂点」と「非隣接頂点」の違いを除けば、議論の流れはほとんど変わらない。
命題 2.3.1 は (コンピューターを使った) 総当たりで証明することもできる。この場合、\(6\) 個の頂点を持つ単純グラフのそれぞれに対して命題が正しいことを確かめれば証明は完了する。なぜなら、頂点が \(6\) 個より多いグラフに対しては頂点をいくつか無視することで頂点が \(6\) 個のグラフに対する「証明」を適用できるからである。頂点が \(6\) 個の単純グラフは (頂点のラベルの置換を同一視すれば) 有限個しか存在せず、そのそれぞれに対して命題 2.3.1 が成り立つかどうかは個別にチェックできる。当然この方法は面倒であり (コンピューターを使ったとしても、\(2^{15}\) 個のグラフで三角形または反三角形を探す処理にはそれなりの時間がかかるだろう)、得られる洞察も少ない。
命題 2.3.1 はラムゼー理論 (Ramsey theory) と呼ばれるグラフ理論の分野で最初に学ぶ結果である。本講義ではラムゼー理論に深入りはしないものの、ここで少しだけ解説させてほしい。命題 2.3.1 に続くのは次に示す一般化である:
\(r\) と \(s\) を正整数とする。\(G\) が \(\left| \operatorname{V}\left( G \right) \right| \geq\dbinom{r+s-2}{r-1}\) を満たす単純グラフのとき、次の二つの命題のうち少なくとも一つが成り立つ:
-
命題 1: \(G\) は互いに隣接する (どの二つも隣接する) \(r\) 個の相異なる頂点を持つ。
-
命題 2: \(G\) は互いに非隣接な (どの二つも隣接しない) \(r\) 個の相異なる頂点を持つ。
命題 2.3.5 で \(r=3\), \(s = 3\) とすると命題 2.3.1 が得られる。
命題 2.3.5 の \(\dbinom{r+s-2}{r-1}\) は改善できないのだろうかと思ったかもしれない ── つまり、\(\left| \operatorname{V}\left( G \right) \right|\) をもっと小さくしても結論は偽にならないのではないだろうか? \(r = 3\), \(s = 3\) の場合には、改善は不可能である: 命題 2.3.1 の数字 \(6\) は小さくできない3。しかし、\(\left| \operatorname{V}\left( G \right) \right|\) を \(\dbinom{r+s-2}{r-1}\) より小さくできる \(r\), \(s\) の値は存在する。例えば \(r=4\), \(s=4\) のとき \(\dbinom{4+4-2}{4-1}=20\) なのに対して、\(\left| \operatorname{V}\left( G \right) \right|\) は \(18\) まで小さくできる。命題 2.3.5 の \(\dbinom{r+s-2}{r-1}\) を置き換えられる最小の自然数をラムゼー数 (Ramsey number) \(R\left( r,s\right) \) と呼ぶ。例えば、これまでに \(R\left( 3,3\right) = 6\) を示した。大きな \(r\) と \(s\) に対する \(R\left(r,s\right)\) の計算は計算論的に難しい問題となる。コンピューターを利用して発見されたラムゼー数の値を次に示す:
ラムゼー数 \(R\left( 5,5\right) \) の値は現在でも分かっていない。ただし \(43\leq R\left( 5,5\right) \leq48\) であることは分かっている。
命題 2.3.5 をさらに一般化すると、ラムゼーの定理 (Ramsey's theorem) という名前で知られる結果となる。この一般化を行うには、少し視点を変える必要がある。まず、単純グラフ \(G\) の代わりに、辺が二つの色 (例えば青と赤) のいずれかで塗られた完全グラフ (全ての異なる二頂点が隣接する単純グラフ) \(K_{n}\) を考える。この置き換えが可能な理由は、\(G\) における「隣接」と「非隣接」が \(K_{n}\) における「青い辺で隣接」と「赤い辺で隣接」に対応するからである。このとき命題 2.3.5 の命題 1 は「青い辺だけで相互に接続された \(r\) 個の相異なる頂点が存在する」となり、命題 2 は「赤い辺だけで相互に接続された \(r\) 個の相異なる頂点が存在する」となる。このように視点を変えると、命題 2.3.5 の一般化が完全グラフ \(K_{n}\) を (二色ではなく) \(k\) 色に塗った場合であることが自然に納得できるだろう。この一般化に関する証明付きの解説、既知のラムゼー数 \(R\left( r,s\right) \) の表、そして命題 2.3.5 の (簡潔ではあるものの) 自己充足的な証明については詳細に書かれた Wikipadia ページ を参照してほしい。ラムゼーの定理にはさらなる一般化や変種が存在し、そういった命題を研究する分野はラムゼー理論 (Ramsey theory) と呼ばれる。ラムゼー理論への基礎的な入門については cut-the-knot.org の記事や上述の Wikipedia ページを参照してほしい。また、Harju [Harju14], Bollobas [Bollob98], West [West01] による教科書も存在する。
命題 2.3.1 は別の方向にも少しだけ改善できる: \(6\) 個以上の頂点を持つ単純グラフ \(G\) は、三角形または反三角形を一つ持つだけではなく、少なくとも二つ持つ (三角形と反三角形を一つずつでも構わない)。この命題の証明はちょうどいい練習問題だろう:
\(G\) を単純グラフとする。\(G\) の三角形または反三角形 (triangle-or-anti-triangle) とは、\(G\) の三角形もしくは反三角形である集合を言う。
-
\(\left\vert \operatorname{V}\left( G\right) \right\vert \geq6\) と仮定する。\(G\) が少なくとも \(2\) 個の三角形または反三角形を持つと示せ。
-
ある \(m\in\mathbb{N}\) が存在して \(\left\vert \operatorname{V}\left( G\right) \right\vert =m+6\) だと仮定する。\(G\) が少なくとも \(m+1\) 個の三角形または反三角形を持つと示せ。