2.5. グラフの同型
異なる二つのグラフが「頂点の名前を無視すれば同じ」ということがある。例えば次の二つのグラフがそうである:
この概念を定式化しよう:
\(G\) と \(H\) を単純グラフとする。
-
全単射 \(\phi\colon\operatorname*{V}\left( G\right) \rightarrow\operatorname*{V}\left( H\right) \) が辺を保存するとき、\(\phi\) を \(G\) から \(H\) へのグラフ同型写像 (graph isomorphism) と呼ぶ。言い換えれば、次の性質を持つ全単射 \(\phi\) をグラフ同型写像と呼ぶ: \(G\) の任意の二頂点 \(u\), \(v\) に対して次の関係が成り立つ:
\[ \left( uv\in\operatorname*{E}\left( G\right) \right) \Longleftrightarrow \left( \phi\left( u\right) \phi\left( v\right) \in\operatorname*{E} \left( H\right) \right) \]グラフ同型写像は単に同型写像 (isomorphism) とも呼ぶ。
-
\(G\) から \(H\) へのグラフ同型写像が存在するとき、\(G\) と \(H\) は同型 (isomorphic) と言い、\(G\cong H\) と書く。
例を二つ示す:
-
次の二つのグラフは同型である:
なぜなら、頂点 \(1,2,3\) をそれぞれ \(1,3,2\) に移す頂点集合間の全単射が同型写像となるためである。頂点 \(1,2,3\) を \(2,3,1\) に移す全単射も同型写像となる。
-
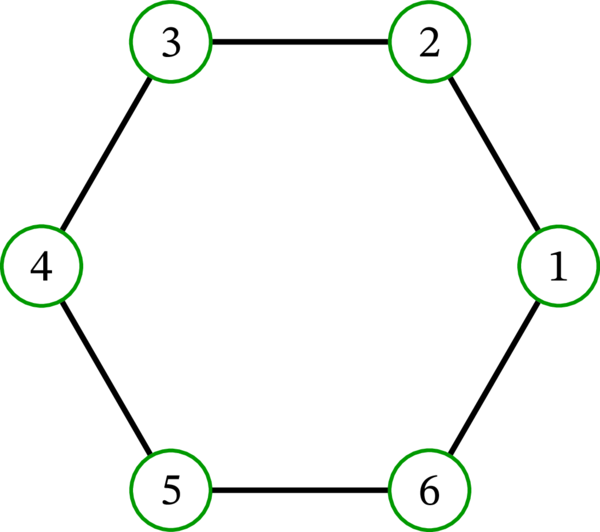
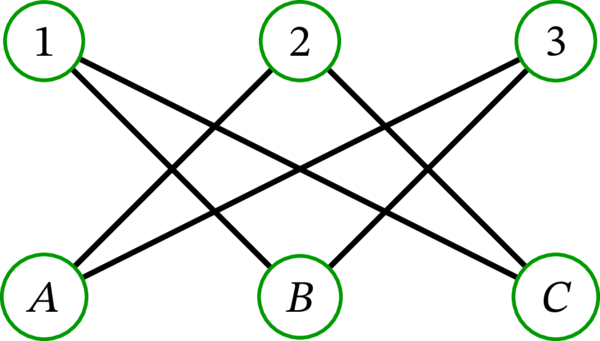
次の二つのグラフは同型である:
なぜなら、頂点 \(1,2,3,4,5,6\) をそれぞれ \(1,B,3,A,2,C\) に移す頂点集合間の全単射が同型写像となるためである。
同型写像の基本的な性質を二つ示す。いずれも証明は易しい:
\(G\) と \(H\) を単純グラフとする。\(G\) から \(H\) へのグラフ同型写像 \(\phi\) が存在するとき、\(\phi\) の逆写像は \(H\) から \(G\) へのグラフ同型写像である。
\(G\), \(H\), \(I\) を単純グラフとする。\(G\) から \(H\) へのグラフ同型写像 \(\phi\) と \(H\) から \(I\) へのグラフ同型写像 \(\psi\) が存在するなら、\(\psi \circ\phi\) は \(G\) から \(I\) へのグラフ同型写像である。
この二つの命題を使えば、\(\cong\) が (全てのグラフからなるクラス上の) 同値関係であることが簡単に示せる。
グラフ同型写像はグラフの「本質的な」性質を全て保存する。この例を示す:
\(G\) と \(H\) を単純グラフ、\(\phi\) を \(G\) から \(H\) へのグラフ同型写像とする。このとき:
-
全ての \(v\in\operatorname*{V}\left( G\right) \) に対して、\(\deg_{G}v=\deg_{H}\left( \phi\left( v\right) \right) \) が成り立つ。ここで \(\deg_{G}v\) は \(G\) の頂点としての \(v\) の次数を表し、\(\deg _{H}\left( \phi\left( v\right) \right) \) は \(H\) の頂点としての \(\phi\left( v\right) \) の次数を表す。
-
\(\left\vert \operatorname*{E}\left( H\right) \right\vert =\left\vert \operatorname*{E}\left( G\right) \right\vert \) が成り立つ。
-
\(\left\vert \operatorname*{V}\left( H\right) \right\vert =\left\vert \operatorname*{V}\left( G\right) \right\vert \) が成り立つ。
グラフ同型写像の用途の一つとして、グラフの頂点に付いている名前の付け替えがある。例えば、\(n\) 個の頂点を持つグラフの頂点を \(1,2,\ldots,n\) (などの \(n\) 個の異なるオブジェクト) に変更するのに利用できる:
\(G\) を単純グラフとする。\(\left\vert S\right\vert =\left\vert \operatorname*{V}\left( G\right) \right\vert \) を満たす任意の有限集合 \(S\) に対して、\(G\) と同型な単純グラフ \(H\) であって \(\operatorname*{V}\left( H\right) =S\) を満たすものが存在する。
易しい。□