2.11. 最長路を使ったトリック

特定の状況でグラフの閉路の存在を保証する命題をもう一つ示す。命題そのものより重要なこととして、この命題の証明で利用されるテクニックはグラフが関係する様々な議論で有用となる:

[証明] \(\mathbf{p}=\left( v_{0},v_{1},\ldots,v_{m}\right) \) を \(G\) における最長の路とする。 [\(G\) が最長の路を持つと言えるのはどうしてだろうか？ 考えてみよう: 路に含まれる頂点は相異なるので、\(G\) における路の長さは最大でも \(\left\vert \operatorname*{V}(G)\right\vert -1\) である。加えて、\(G\) は少なくとも一つの頂点を持つので、\(G\) における路は少なくとも一つ存在する。整数の非空有限集合には最大要素が存在するので、\(G\) は最長の路を持つ。]

問題の仮定より、頂点 \(v_{0}\) の次数は \(d\) 以上である。次数とは隣接頂点の個数だから、\(v_{0}\) は \(d\) 個以上の隣接頂点を持つ。

もし \(v_{0}\) の全ての隣接頂点が集合 \(\left\{ v_{1},v_{2},\ldots,v_{d-1}\right\} \)¹ に属するなら、\(v_{0}\) の隣接頂点の個数は最大でも \(d-1\) 個となるものの、これは前段落と矛盾する。よって集合 \(\left\{ v_{1},v_{2},\ldots,v_{d-1}\right\} \) に属さない \(v_{0}\) の隣接頂点 \(u\) が存在する。任意の頂点は自身の隣接頂点となれないので、\(u \neq v_{0}\) が成り立つ。

頂点 \(u\) を路 \(\mathbf{p}\) の先頭に加えると、次の歩道 \(\mathbf{p}^{\prime}\) を得る:

もし \(u\notin\left\{ v_{0},v_{1},\ldots,v_{m}\right\} \) なら、この歩道 \(\mathbf{p}^{\prime}\) は路である。しかし、これは \(\mathbf{p}\) が \(G\) における最長の路である事実と矛盾する。よって \(u\in\left\{ v_{0},v_{1},\ldots,v_{m}\right\} \) でなければならない。言い換えれば、ある \(i\in\left\{ 0,1,\ldots,m\right\} \) で \(u = v_{i}\) が成り立つ。この \(i\) に注目すると、\(u\neq v_{0}\) と \(u\notin\left\{ v_{1},v_{2},\ldots,v_{d-1}\right\} \) から \(i \geq d\) が分かる。以上の様子を次の図に示す:

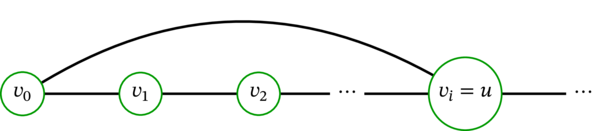
続いて、次の歩道 \(\mathbf{c}\) を考える:

\(u = v_{i}\) なので \(\mathbf{c}\) は閉歩道であり、その長さは \(i + 1 \geq d + 1\) である。よって \(\mathbf{c}\) が閉路だと示せれば、長さが \(d + 1\) 以上の閉路を見つけたことになって証明が完了する。

よって \(\mathbf{c}\) が閉路だと示せばよい。このためには「\(\mathbf{c}\) の頂点 \(u,v_{0},v_{1},\ldots,v_{i-1}\) が相異なる」と「\(\mathbf{c}\) の長さが \(3\) 以上」を示す必要がある。後者は易しい: \(d > 1\) と \(d \in \mathbb{Z}\) から \(i+1\geq d+1\geq3\) を得る。前者は少しだけ難しい: \(u=v_{i}\) より頂点 \(u,v_{0},v_{1},\ldots,v_{i-1}\) は実際には \(v_{i},v_{0},v_{1},\ldots,v_{i-1}\) だと分かる。これらは全て路 \(\mathbf{p}\) の頂点なので相異なる。以上で命題 2.11.1 は証明された。□