2.7. 部分グラフ
\(G=\left( V,E\right) \) を単純グラフとする。
-
\(G\) の部分グラフ (subgraph) とは、頂点集合 \(W\subseteq V\) と辺集合 \(F\subseteq E\) からなる単純グラフ \(H=\left( W,F\right) \) を言う。言い換えれば、\(G\) の部分グラフとは頂点が \(G\) の頂点で辺が \(G\) の辺である単純グラフを言う。
-
\(S\) を \(V\) の部分集合とする。単純グラフ \(\left( S,\ \ E\cap\mathcal{P}_{2}\left( S\right) \right)\) を集合 \(S\) に関する \(G\) の誘導部分グラフ (induced subgraph of \(G\) on the set \(S\)) と呼ぶ。言い換えれば、この単純グラフは \(G\) の部分グラフであり、頂点は \(S\) の要素、辺は両端が \(S\) に含まれる \(G\) の辺からなる。
-
\(G\) の誘導部分グラフ (induced subgraph) とは、何らかの \(S \subseteq V\) に関する \(G\) の誘導部分グラフを意味する。
つまり、単純グラフ \(G\) の部分グラフは \(G\) から頂点と辺をいくつか取り去れば手に入る (もちろん、辺が「浮いている」状態になってはいけない ── 頂点を取り去ったときは、その頂点を含む辺も全て取り去る必要がある)。頂点だけを取り去り、辺を個別に取り去らない場合 (端点のいずれかを失った辺だけを取り去る場合)、手に入る部分グラフは誘導部分グラフとなる。このため、誘導部分グラフは次のように特徴付けられる:
\(H\) を単純グラフ \(G\) の部分グラフとする。このとき、\(H\) が \(G\) の誘導部分グラフとなるのは、端点 \(u\), \(v\) がどちらも \(\operatorname*{V}\left( H\right) \) に属する \(G\) の辺 \(uv\) が全て \(H\) の辺であるときであり、かつそのときに限る。
定義を理解したかどうかの問題である。□
\(n > 1\) を整数とする。
-
路グラフ \(P_{n}\) は閉路グラフ \(C_{n}\) の部分グラフである。しかし \(n > 2\) のとき \(P_{n}\) は \(C_{n}\) の誘導部分グラフでない: \(P_{n}\) は \(C_{n}\) の頂点 \(n\) と \(1\) を含むのに対して、\(C_{n}\) の辺 \(n1\) は \(P_{n}\) の辺ではない。
-
路グラフ \(P_{n-1}\) は \(P_{n}\) の誘導部分グラフである (具体的に言えば、集合 \(\left\{ 1,2,\ldots,n-1\right\}\) に関する \(P_{n}\) の誘導部分グラフが \(P_{n-1}\) である)。
-
\(n > 3\) とする。\(C_{n-1}\) は \(C_{n}\) の部分グラフだろうか? 辺 \(\left( n-1\right) 1\) は \(C_{n-1}\) に存在するのに対して \(C_{n}\) には存在しないので、\(C_{n-1}\) は \(C_{n}\) の部分グラフではない。
次の命題は簡単に示せる:
\(G\) を単純グラフ、\(H\) を \(G\) の部分グラフとする。\(H\) が完全グラフのとき、\(H\) は \(G\) の誘導部分グラフである。
\(H\) が完全グラフなので、\(H\) の頂点集合の二要素部分集合は全て \(H\) の辺である。よって命題 2.7.2 から \(H\) は \(G\) の誘導部分グラフと分かる。□
なお、グラフ中の三角形は完全部分グラフとして特徴付けられる。つまり、単純グラフの三角形は三頂点の完全部分グラフそのものである:
\(G\) を単純グラフ、\(G\) の相異なる三頂点を \(u\), \(v\), \(w\) とする。次の三つの命題は同値である:
-
\(\left\{ u,v,w\right\} \) が \(G\) の三角形である。
-
\(\left\{ u,v,w\right\} \) に関する \(G\) の誘導部分グラフが \(K_{3}\) と同型である。
-
\(\left\{ u,v,w\right\} \) に関する \(G\) の誘導部分グラフが \(C_{3}\) と同型である。
このため、「\(G\) の三角形」と言う代わりに「\(G\) 内の \(K_{3}\)」や「\(C_{3}\) 内の \(G\)」と言うことがある。一般に、単純グラフ \(G\), \(H\) に対する「\(G\) 内の \(H\)」は \(H\) と同型な \(G\) の部分グラフを指す。
\(n\) を正整数、\(S\) を \(2n\) 個の頂点を持つ単純グラフとする。\(S\) は偶数個の隣接頂点を持つ相異なる二頂点を持つことを示せ。
\(n > 2\) を整数、\(G\) を \(n\) 個の頂点を持つ単純グラフとする。
-
\(G\) の頂点の次数が \(1,1,\ldots,1,n-1\) のとき、\(G\) を描写せよ。
-
正整数 \(a\), \(b\) が \(a + b = n\) を満たすとする。\(G\) の頂点の次数が \(1,1,\ldots,1,a,b\) のとき、\(G\) を描写せよ。
「\(G\) を描写する」とは、\(G\) と同型なグラフを (証明付きで) 明示的に示すことを意味する。
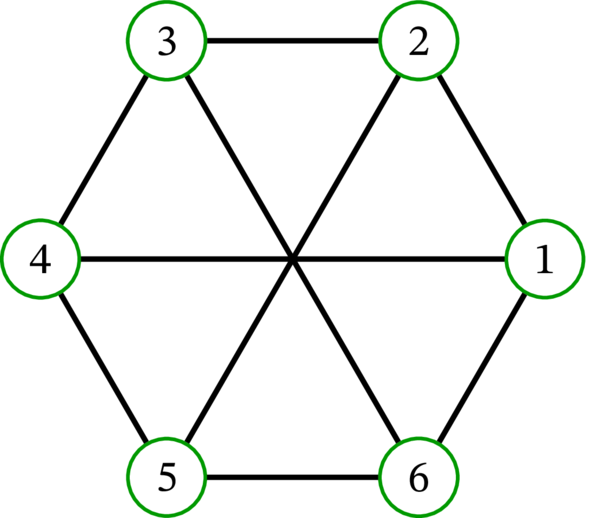
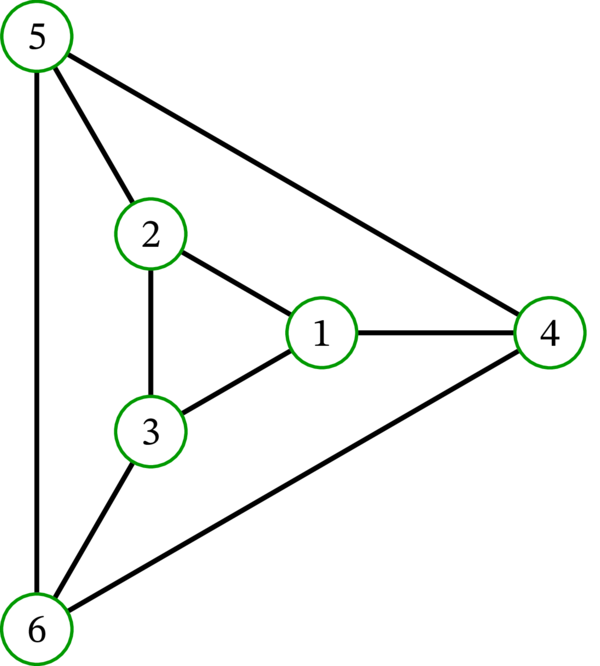
練習問題 2.8 の状況は、ある意味で例外的と言える。頂点の次数が与えられただけでグラフが同型を除いて確定することは一般にない。例えば、次の二つのグラフは同型でない1ものの、頂点の次数は同じである (全ての頂点が次数 \(3\) を持つ)。
-
この事実は三角形 (互いに隣接する相異なる三頂点) の有無に注目すると簡単に確認できる。二つ目のグラフは三角形を持つのに対して、一つ目のグラフは三角形を持たない。 ↩︎