2.9. グラフの歩道と路

目次

本節ではついに歩道と路を定義する ── どちらもグラフに関連する最も基礎的な概念の一つである。グラフに初めて言及した Euler による 1736 年の論文は、とある特徴を持つ歩道を議論した。

2.9.1定義

グラフが道路ネットワークを表すと想像してほしい。頂点は街に、辺は (双方向の) 道に対応する。いくつかの道を経由すれば、ある街から隣接していない別の町に移動できる。これを数学的に定義すると歩道となる:

定義 2.9.1

\(G\) を単純グラフとする。

  1. \(G\) における歩道 (walk) とは、\(G\) の頂点の有限列 \(\left( v_{0},v_{1},\ldots,v_{k}\right) \) (\(k \geq 0\)) であって、\(v_{0}v_{1}\), \(v_{1}v_{2}\), \(v_{2}v_{3}\), ..., \(v_{k-1}v_{k}\) が全て \(G\) の辺であるものを言う (\(k = 0\) のとき後半の条件は空虚な真となる)。

  2. \(\mathbf{w}=\left( v_{0},v_{1},\ldots,v_{k}\right) \) を \(G\) における歩道とする。このとき:

    • \(\mathbf{w}\) の頂点 (vertex) は \(v_{0},v_{1},\ldots,v_{k}\) と定義される。

    • \(\mathbf{w}\) の辺 (edge) は \(v_{0}v_{1},\ v_{1}v_{2},\ v_{2}v_{3},\ \ldots,\ v_{k-1}v_{k}\) と定義される。

    • 非負整数 \(k\) を \(\mathbf{w}\) の長さ (length) と呼ぶ。 [歩道 \(\mathbf{w}\) の長さは \(\mathbf{w}\) の辺の個数に等しく、\(\mathbf{w}\) の頂点の個数より \(1\) だけ小さい。ここで重複する辺/頂点は別のものとして数える。]

    • 頂点 \(v_{0}\) を \(\mathbf{w}\) の始点 (starting point) と呼ぶ。\(\mathbf{w}\) を「\(v_{0}\) から始まる歩道」と言う。

    • 頂点 \(v_{k}\) を \(\mathbf{w}\) の終点 (ending point) と呼ぶ。\(\mathbf{w}\) を「\(v_{k}\) で終わる歩道」と言う。

  3. \(G\) における路 (path) とは、異なる頂点からなる \(G\) における歩道を言う。言い換えれば、路は \(v_{0},v_{1},\ldots,v_{k}\) が相異なる歩道 \(\left( v_{0},v_{1},\ldots,v_{k}\right) \) を意味する。

  4. \(p\) と \(q\) を \(G\) の二頂点とする。\(p\) から \(q\) への歩道 (walk from \(p\) to \(q\)) とは、\(p\) から始まって \(q\) で終わる歩道を言う。\(p\) から \(q\) への路 (path from \(p\) to \(q\)) とは、\(p\) から始まって \(q\) で終わる路を言う。

  5. 「\(G\) における歩道 (walk in \(G\))」「\(G\) における路 (path in \(G\))」と言う代わりに「\(G\) の歩道 (walk of \(G\))」「\(G\) の路 (path of \(G\))」と言う場合がしばしばある。

例 2.9.2

\(G\) を次のグラフとする:

\[ \left( \left\{ 1,2,3,4,5,6\right\} ,\ \ \left\{ 12,\ 23,\ 34,\ 45,\ 56,\ 61,\ 13\right\} \right) \]

このグラフの描画を次に示す:

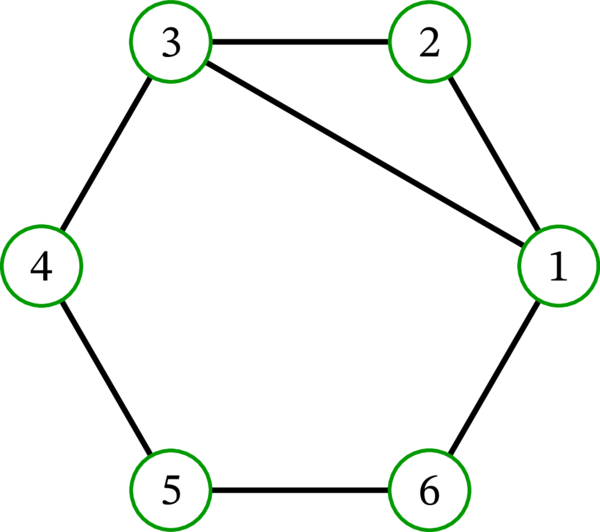
このとき:

  • \(G\) の頂点の列 \(\left( 1,3,4,5,6,1,3,2\right) \) は \(G\) における歩道である。この歩道は \(1\) から \(2\) への歩道であり、この歩道の長さは \(7\) である。

  • \(G\) の頂点の列 \(\left( 1,2,4,3\right) \) は歩道ではない。\(24\) が \(G\) の辺でないためである。そのため、この頂点の列は路でもない。

  • 頂点の列 \(\left( 1,3,2,1\right) \) は \(1\) から \(1\) への歩道である。この歩道の長さは \(3\) である。この歩道は路でない。

  • 頂点の列 \(\left( 1,2,1\right) \) は \(1\) から \(1\) への歩道である。この歩道の長さは \(2\) である。この歩道は路でない。

  • 列 \(\left(5\right)\) は \(5\) から \(5\) への歩道である。この歩道の長さは \(0\) である。この歩道は路でもある。一般に、\(G\) の各頂点 \(v\) からは長さ \(0\) の路 \(\left( v\right) \) を構築できる。

  • 列 \(\left( 5,4\right) \) は \(5\) から \(4\) への歩道である。この歩道の長さは \(1\) である。この歩道は路でもある。一般に、\(G\) の各辺 \(uv\) からは長さ \(1\) の路 \(\left( u,v\right) \) を構築できる。

直感的には、歩道と路の定義は次のように言い換えられる:

練習問題 2.9

\(G\) を単純グラフ、\(\mathbf{w}\) を \(G\) の路とする。\(\mathbf{w}\) の辺が相異なることを示せ。 [これはグラフを描画すれば明らかである。厳密な証明を書いてみよ！]

[解答: これは 2017 年春学期に開講された講義で出した homework set #1 の Exercise 3 である。解答は講義ページに載っている。]

2.9.2歩道/路の連結と反転

続いて、歩道と路に関する簡単な操作を二つ定義する。

まず、ある歩道の終点と別の歩道の始点が同じなら、その二つの歩道は「連結」できる:

命題 2.9.3

\(G\) を単純グラフ、\(u\), \(v\), \(w\) を \(G\) の三頂点、\(\mathbf{a}=\left( a_{0},a_{1},\ldots ,a_{k}\right) \) を \(u\) から \(v\) への歩道、\(\mathbf{b}=\left( b_{0},b_{1},\ldots,b_{\ell}\right) \) を \(v\) から \(w\) への歩道とする。このとき

\[ \begin{aligned} \left( a_{0},a_{1},\ldots,a_{k},b_{1},b_{2},\ldots,b_{\ell}\right) & =\left( a_{0},a_{1},\ldots,a_{k-1},b_{0},b_{1},\ldots,b_{\ell}\right) \\ & =\left( a_{0},a_{1},\ldots,a_{k-1},v,b_{1},b_{2},\ldots,b_{\ell}\right) \end{aligned} \]

は \(u\) から \(w\) への歩道である。この歩道を今後 \(\mathbf{a}\ast\mathbf{b}\) と表記する。

[証明] 直感的に明らかであり、証明も易しい。□

命題 2.9.4

\(G\) を単純グラフ、\(u\) と \(v\) を \(G\) の二頂点とする。\(\mathbf{a}=\left( a_{0},a_{1},\ldots,a_{k}\right) \) を \(u\) から \(v\) への歩道とする。このとき:

  1. \(\left( a_{k},a_{k-1},\ldots,a_{0}\right) \) は \(v\) から \(u\) への歩道である。この歩道を今後 \(\operatorname*{rev}\mathbf{a}\) と表記し、\(\mathbf{a}\) の反転 (reversal) と呼ぶ。

  2. \(\mathbf{a}\) が路なら、\(\operatorname*{rev}\mathbf{a}\) も路となる。

[証明] 直感的に明らかであり、証明も易しい。□

2.9.3歩道から路への変換

路は頂点が重複しない歩道と定義される。もし歩道を手にしているなら、そこから「ループ」(別の言い方をすれば「寄り道」) を除去することで路を構築できる:

命題 2.9.5

\(G\) を単純グラフ、\(u\) と \(v\) を \(G\) の二頂点、\(\mathbf{a}=\left( a_{0},a_{1},\ldots,a_{k}\right) \) を \(u\) から \(v\) への歩道とする。さらに、\(\mathbf{a}\) は路でないとする。このとき、\(u\) から \(v\) への歩道であって長さが \(k\) より小さいものが存在する。

[証明] \(\mathbf{a}\) が路でないので、\(\mathbf{a}\) の頂点には重複するものが含まれる。言い換えれば、\(i < j\) かつ \(a_{i}=a_{j}\) を満たす \(i\), \(j\) が存在する。この \(i\) と \(j\) を使って定義される次の列を考える:

\[ \left( \underbrace{a_{0},a_{1},\ldots,a_{i}}_{\mathbf{a} \text{ の最初の } i+1 \text{ 頂点}}, \underbrace{a_{j+1},a_{j+2},\ldots,a_{k}}_{\mathbf{a} \text{ の最後の } k-j\text{ 頂点 }} \right) \]

[これは \(\mathbf{a}\) の \(a_{i}\) から \(a_{j}\) までの部分を除去した列である。] この列は \(u\) から \(v\) への歩道であり、その長さは \(\underbrace{i}_{< j}+\left( k-j\right) < j+\left( k-j\right) =k\) である。\(u\) から \(v\) への歩道で長さが \(k\) より小さいものが見つかったので、命題 2.9.5 は証明された。□

例 2.9.6

例 2.9.2 の歩道 \(\left( 1,3,4,5,6,1,3,2\right) \) を考える。命題 2.9.5 からは \(1\) から \(2\) への歩道であって長さがこの歩道より小さいものが存在すると分かる。この条件を満たす歩道は二つの \(3\) の間にある頂点を除去することで得られる。こうして得られる歩道 \(\left( 1,3,2\right) \) は実際には路である。

系 2.9.7

[歩道あるところに路あり] \(G\) を単純グラフ、\(u\) と \(v\) を相異なる \(G\) の二頂点とする。\(u\) から \(v\) への長さ \(k \in \mathbb{N}\) の歩道が存在するなら、 \(u\) から \(v\) への路であって長さが \(k\) 以下のものが存在する。

[証明] 命題 2.9.5 より、\(u\) から \(v\) への路でない歩道が存在するなら、それより短い \(u\) から \(v\) への歩道が存在することが分かる。この命題を繰り返し適用すると、最終的には路が得られる (いずれ必ず路が手に入ることは、歩道の長さが無限に小さくなり続けることはない事実から分かる)。

2.9.4歩道と路に関するアルゴリズム

構造的な定理の証明は一旦脇に置いて、本項では計算論的に重要な問題を考える。本書のような講義ノートの宿命として、この解説は表面をなでるだけに過ぎず、紹介されるアルゴリズムは厳密には最適でない。

単純グラフ \(G\) と \(G\) の二頂点 \(u\), \(v\) が与えられたとき、次の質問を考えることができる:

質問 1: \(G\) は \(u\) から \(v\) への歩道を持つかどうかを答えよ。

質問 2: \(G\) は \(u\) から \(v\) への路を持つかどうかを答えよ。

質問 3: \(u\) から \(v\) への最短路 (shortest path, \(u\) から \(v\) への路で長さが最も小さいもの) を見つけるか、最短路が存在しないなら「存在しない」と答えよ。

質問 4: 与えられた \(k \in \mathbb{N}\) に対して、\(u\) から \(v\) への歩道であって長さが \(k\) のものを見つけるか、そのような歩道が存在しないなら「存在しない」と答えよ。

質問 5: 与えられた \(k \in \mathbb{N}\) に対して、\(u\) から \(v\) への路であって長さが \(k\) のものを見つけるか、そのような路が存在しないなら「存在しない」と答えよ。

系 2.9.7 からは質問 1 と質問 2 が等価であることが分かる (実際、\(u\) から \(v\) への歩道の存在は \(u\) から \(v\) への路の存在を意味することが系 2.9.7 から分かる。逆は定義より自明に分かる)。また明らかに、質問 3 は質問 2 より強い: つまり、質問 3 に答えるアルゴリズムを使えば質問 2 にも答えられる。

もう少し考えると、質問 4 が質問 3 より強いことが容易に分かる。実際、系 2.9.7 より \(u\) から \(v\) への最短歩道は (もし存在するなら) \(u\) から \(v\) への最短路でなければならないと分かる。\(G\) の頂点数を \(n\) とすれば \(u\) から \(v\) への任意の路は長さが \(n-1\) 以下である (長さ \(k\) の路は \(k+1\) 個の相異なる頂点を持ち、\(G\) には \(n\) 個しか頂点がないため)。よって、\(u\) から \(v\) への長さ \(n-1\) 以下の歩道が存在しなければ、\(u\) から \(v\) への路が存在しないと分かる。従って、全ての \(k\in\left\{ 0,1,\ldots,n-1\right\} \) に対する質問 4 への解答があれば、\(u\) から \(v\) への最短路もしくは \(u\) から \(v\) への最短路が存在しない事実を確実に知ることができる。 [上述の議論から、質問 4 の解答が歩道となる最小の \(k\) に対応する歩道が最短路となる。もし \(k\in\left\{ 0,1,\ldots,n-1\right\} \) の全てに対して質問 4 の解答が「存在しない」なら、質問 3 の解答も「存在しない」となる。]

よって、質問 4 に答えるアルゴリズムを使えば質問 1, 2, 3 にも答えられる。

これから再帰的なアルゴリズムを使って質問 4 に答える方法を大まかに説明する。まず、このアルゴリズムは \(k\) に関して再帰的に問題を解く。ベースケース \(k=0\) は簡単に処理できる: \(u\) から \(v\) への長さ \(0\) の歩道は \(u=v\) なら存在し、そうでないなら存在しない。面白いのは再帰ステップである: \(k\) を正整数として、\(k-1\) に対する質問 4 に答えられると仮定する。このとき、どうすれば \(k\) に対する質問 4 に答えられるだろうか？ まず、\(u\) から \(v\) への長さ \(k\) の歩道は \(\left( u,\ldots,w,v\right) \) の形をしていることに注目する。ここで \(w\) は最後から二番目の頂点であり、\(v\) と隣接する。さらに、最後の頂点 \(v\) を歩道 \(\left( u,\ldots,w,v\right) \) から取り除くと、長さ \(k-1\) の歩道 \(\left( u,\ldots,w\right) \) が得られる。ここから、\(u\) から \(v\) への長さ \(k\) の歩道が次のアルゴリズムで得られることが分かる:

質問 4 に解答するこの再帰的アルゴリズムは、適切に実装されれば、現実世界の問題で利用できるほどの速度で動作する。 [このアルゴリズムは複雑性理論 (complexity theory) の分野で多項式時間アルゴリズムと呼ばれる特徴を持つ1。] ただし、これより格段に高速なアルゴリズムも存在する。実際の応用では、質問 3 を一般化した「(長さではなく) 重み付き長さが最小の路を求めよ」という問題がよく現れる。つまり、この問題では辺ごとに「長さ」への寄与が異なる。この一般化されたバージョンの問題は計算機科学の分野で最も基礎的なアルゴリズム的問題の一つであり、最短路問題 (shortest path problem) と呼ばれる。最短路問題を解くアルゴリズムは Wikipedia やアルゴリズムが中心の教科書 [Griffi21, § 3.5], [KelTro17, § 12.3], [Schrij17, Chapter 1], (徹底的に勉強したい場合は) [Schrij03, Chapters 6–8] で詳しく解説されている。

質問 5 は質問 4 とよく似ているものの、次の重要な点で異なる: 質問 5 に答える効率的なアルゴリズムは知られていない！ この問題は複雑性理論の分野で NP 困難問題 (NP-hard problem) と呼ばれる区分に属する。この区分に属する問題に対する多項式時間アルゴリズムは存在しないと誰もが思っている (しかし、そのことは現在の人類が持つ知識では証明できないと見られている)。質問 5 は突き詰めれば有限の問題である (\(G\) の路は有限個しか存在しないので、それらを全てチェックしていけば答えは出る) 上に、\(k\) を固定すれば多項式時間アルゴリズムが存在する (上述したアルゴリズムに似た自明なもの: \(G\) の頂点 \(k+1\) 個からなる列を走査し、その列が \(u\) から \(v\) への路かどうかを調べる。調べる必要のある列は全部で \(n^{k+1}\) 個ある)。しかし、このアルゴリズムは \(k\) に関して指数的に増加する複雑性を持つので、現実世界の問題を解くのには利用できない。

2.9.5路連結性

歩道と路の概念を使うと、任意のグラフ \(G\) の頂点集合 \(\operatorname*{V}\left( G\right) \) 上に次の同値関係を定義できる:

定義 2.9.8

\(G\) を単純グラフとする。集合 \(\operatorname*{V}\left( G\right) \) 上に二項関係 \(\simeq_{G}\) を次のように定義する: \(G\) の二頂点 \(u\), \(v\) に対して、\(u\) から \(v\) への歩道が存在するとき、かつそのときに限って \(u\simeq_{G}v\) が成立する。

この二項関係 \(\simeq_{G}\) を路連結性 (path-connectedness) または単に連結性 (connectedness) と呼ぶ。二頂点 \(u\), \(v\) が \(u\simeq_{G}v\) を満たすとき、\(u\) と \(v\) は路連結 (path-connected) と言う。

命題 2.9.9

\(G\) を単純グラフとする。\(\simeq_{G}\) は同値関係である。

[証明] \(\simeq_{G}\) が対称性、反射性、推移性を持つことを示す必要がある。

以上で命題 2.9.9 は証明された。□

命題 2.9.10

\(G\) を単純グラフ、\(u\), \(v\) を \(G\) の二頂点とする。\(u\) から \(v\) への路が存在するとき、かつそのときに限って \(u\simeq_{G}v\) が成立する。

[証明] \(\Longleftarrow\): 任意の路は歩道なので自明に分かる。

\(\Longrightarrow\): 証明すべき命題は「\(u\) から \(v\) への歩道が存在するなら、\(u\) から \(v\) への路が存在する」と言い換えられる。これは系 2.9.7 から従う。□

2.9.6連結成分と連結性

定義 2.9.8 で導入した同値関係 \(\simeq_{G}\) からは、二つの重要な概念が定義できる:

定義 2.9.11

\(G\) を単純グラフとする。同値関係 \(\simeq_{G}\) の同値類を \(G\) の連結成分 (connected component) と呼ぶ。連結成分は単に成分 (component) とも呼ぶ。

定義 2.9.12

\(G\) を単純グラフとする。\(G\) の成分がちょうど一つのとき、\(G\) は連結 (connected) と言う。

つまり、単純グラフ \(G\) が連結なのは \(G\) が成分を一つ以上持ち (少なくとも一つの頂点を持ち)、加えて成分を二つ以上持たないとき (任意の二つの頂点が路連結なとき) であり、かつそのときに限る。

例 2.9.13

頂点集合が \(\left\{ 1,2,\ldots,9\right\} \) で、任意の二頂点 \(i\), \(j\) が \(\left\vert i-j\right\vert =3\) を満たすとき、かつそのときに限って頂点が隣接するグラフを \(G\) とする。\(G\) の成分は何か？

グラフ \(G\) の描画を示す:

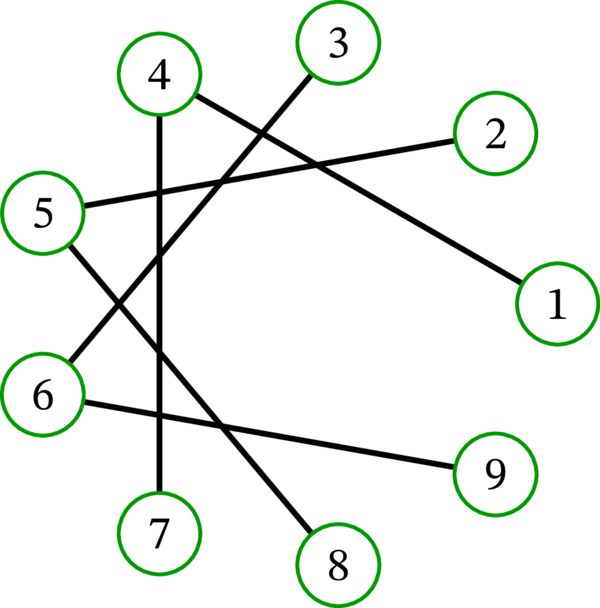
辺がたくさん引かれているので、全ての頂点が相互に路連結だと思うかもしれない。しかし、描画で交差する辺が必ずしも端点を共有するわけではない。歩道は共通の端点を持つ辺しか使えないので、\(G\) が持つ歩道は見かけよりも少ない。成り立つのは \(1\simeq_{G}4\simeq_{G}7\), \(\,2\simeq_{G}5\simeq_{G}8\), \(\,3\simeq_{G}6\simeq_{G}9\) だけである。実際、\(G\) の任意の二頂点は (整数として見たとき) \(3\) を法として合同なときに限って隣接するので、\(G\) の辺を通って到達できるのは法が \(3\) の合同類で始点と同じ集合に属する頂点に限られる。よって \(G\) の成分は \(\left\{ 1,4,7\right\} \), \(\left\{ 2,5,8\right\} \), \(\left\{ 3,6,9\right\} \) の三つである。\(G\) は連結でない。

例 2.9.14

頂点集合が \(\left\{ 1,2,\ldots,9\right\} \) で、任意の二頂点 \(i\), \(j\) が \(\left\vert i-j\right\vert =6\) を満たすとき、かつそのときに限って隣接するグラフを \(G\) とする。このグラフ \(G\) の描画を示す:

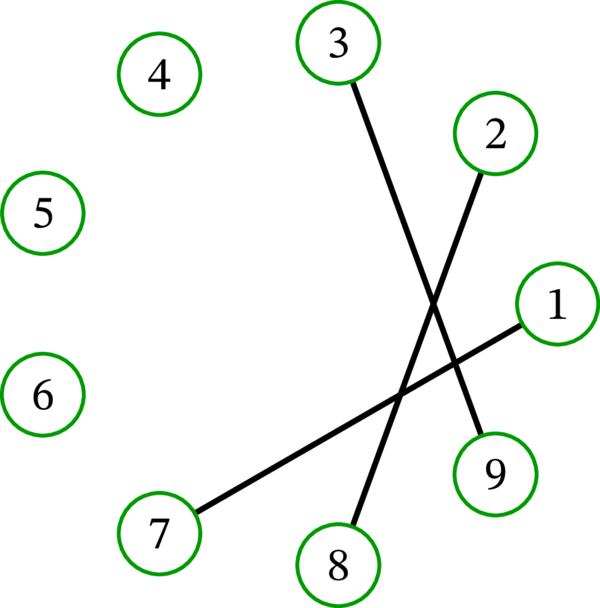
\(G\) の成分は何だろうか？ \(G\) の成分は \(\left\{ 1,7\right\} \), \(\left\{ 2,8\right\} \), \(\left\{ 3,9\right\} \), \(\left\{ 4\right\} \), \(\left\{ 5\right\} \), \(\left\{ 6\right\} \) である。六つある成分の三つは単元集合であることに注意してほしい。\(G\) は連結でない。

例 2.9.15

頂点集合が \(\left\{ 1,2,\ldots,9\right\} \) で、任意の二頂点 \(i\), \(j\) が \(\left\vert i-j\right\vert =3\) または \(\left\vert i-j\right\vert =4\) を満たすとき、かつそのときに限って隣接するグラフを \(G\) とする。このグラフ \(G\) の描画を示す:

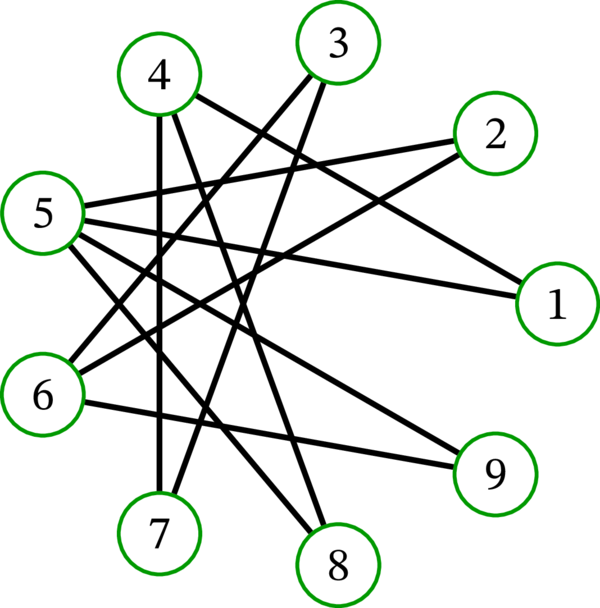
\(G\) には次の長い歩道が存在する:

\[ \left( 1,4,7,3,6,9,5,2,5,8\right) \]

この歩道は \(G\) の全ての頂点を通るので、\(G\) の任意の二頂点は路連結である。よって \(G\) の成分は \(\left\{ 1,2,\ldots,9\right\} \) の一つしか存在しない。\(G\) は連結である。

例 2.9.16

空でない集合上の完全グラフは連結である。空集合上の完全グラフは成分の個数が (\(1\) ではなく) \(0\) なので、連結でない。

例 2.9.17

有限集合 \(V\) 上の空グラフは \(\left\vert V\right\vert \) 個の成分を持つ (具体的には、各頂点 \(v \in V\) に対する単元集合 \(\left\{ v\right\} \) が成分となる)。このため、\(V\) 上の空グラフは \(\left\vert V\right\vert =1\) のとき、かつそのときに限って連結となる。

練習問題 2.10

\(S\) を有限集合、\(k \in \mathbb{N}\) とする。

定義 2.6.4 で見たように、Kneser グラフ \(K_{S,k}\) の頂点は \(k\) 個の要素を持つ \(S\) の部分集合であり、\(K_{S,k}\) の任意の二頂点 \(A\), \(B\) は \(A\cap B=\varnothing\) を満たすとき、かつそのときに限って隣接する。

\(\left\vert S\right\vert \geq 2k+1\) なら Kneser グラフ \(K_{S,k}\) は連結だと示せ。

[Remark: 「Kneser グラフ \(K_{S,k}\) が連結なのは \(\left\vert S\right\vert \geq 2k+1\) のとき、かつそのときに限る」という命題は正しいだろうか？ この命題は正確に言うと正しくない。なぜなら、\(\left\vert S\right\vert =2\), \(k=1\) のとき (\(K_{S,k}\) は二つの頂点と一つの辺からなる)、\(\left\vert S\right\vert =k\) のとき (\(K_{S,k}\) は一つの頂点からなる)、そして \(k=0\) のとき (\(K_{S,k}\) は一つの頂点からなる) \(K_{S,k}\) は連結となるためである。ただし、この命題の「例外」はここに示した三つしか存在しない。]

2.9.7成分に関する誘導部分グラフ

次の命題を理解するのは難しくない:

命題 2.9.18

\(G\) を単純グラフ、\(C\) を \(G\) の成分とする。

このとき、集合 \(C\) に関する \(G\) の誘導部分グラフは連結である。

[証明] \(C\) に関する \(G\) の誘導部分グラフを \(G\left[ C\right] \) とする。\(G\left[ C\right] \) が連結だと示す必要がある。言い換えれば、\(G\left[ C\right] \) の成分の個数がちょうど一つだと示す必要がある。

明らかに、\(G\left[ C\right] \) は少なくとも一つの頂点を持つ (\(C\) は成分、つまり \(\simeq_{G}\) の同値類であり、同値類は空でない)。よって \(G\left[ C\right] \) の成分の個数は \(1\) 以上と分かる。後は \(G\left[ C\right] \) の成分の個数が \(1\) より多くないことを示せばよい。言い換えれば、\(G\left[ C\right] \) の任意の二頂点が \(G\left[ C\right] \) で路連結なことを示す必要がある。

\(u\) と \(v\) を \(G\left[ C\right] \) の二頂点とする。\(C\) が \(G\) の成分なので、\(u,v \in C\) より \(u \simeq_{G} v\) が分かる。つまり、\(u\) から \(v\) への \(G\) における歩道 \(\mathbf{w}=\left( w_{0},w_{1},\ldots ,w_{k}\right) \) が存在する。この歩道 \(\mathbf{w}\) が \(G\left[ C\right] \) における歩道でもあることをこれから示す。このためには、\(\mathbf{w}\) の全ての頂点が \(C\) に属することを証明する必要がある。

これは簡単に証明できる: \(\mathbf{w}\) の任意の頂点 \(w_{i}\) に対して \(\left( w_{0},w_{1},\ldots,w_{i}\right) \) は \(u\) から \(w_{i}\) への \(G\) における歩道なので、\(u\simeq_{G}w_{i}\) が成り立つ。つまり \(w_{i}\) は \(G\) において \(u\) と同じ成分に属する。\(u\) が属する成分は \(C\) だったから、\(\mathbf{w}\) の各頂点 \(w_{i}\) が \(C\) に含まれることがこれで証明できた。従って、\(\mathbf{w}\) は \(G\left[ C\right] \) における歩道である。ここから \(u\simeq_{G\left[ C\right] }v\) が分かる。

\(G\left[ C\right] \) の任意の二頂点 \(u\), \(v\) に対して \(u\simeq_{G\left[ C\right] }v\) が成り立つことが以上で示せた。よって関係 \(\simeq_{G\left[ C\right] }\) の同値類の個数は \(1\) である。言い換えれば、\(G\left[ C\right] \) の成分の個数は \(1\) である。□

次の命題では、単純グラフ \(G\) と \(G\) の頂点集合の部分集合 \(S\) に対して、\(S\) に関する \(G\) の誘導部分グラフを \(G\left[ S\right] \) と表す記法を使っている。

命題 2.9.19

\(G\) を単純グラフ、\(C_{1},C_{2},\ldots,C_{k}\) を重複なく並べた \(G\) の全成分とする。

このとき、非交和 \(G\left[ C_{1}\right] \sqcup G\left[ C_{2}\right] \sqcup\cdots\sqcup G\left[ C_{k}\right] \) は \(G\) と同型である。

[証明] 次の全単射を考える:

\[ \begin{aligned} \operatorname*{V}\left( G\left[ C_{1}\right] \sqcup G\left[ C_{2}\right] \sqcup\cdots\sqcup G\left[ C_{k}\right] \right) &\rightarrow \operatorname*{V} (G) \\ \left( i,v\right) &\mapsto v \end{aligned} \]

この全単射がグラフ同型写像であることをこれから示す。これを示すには、異なる成分に属する二頂点を接続する \(G\) の辺が存在しないことを示す必要がある。これは簡単に分かる: もし \(G\) の異なる成分に属する二頂点が隣接するなら、その二頂点は路連結であり、同じ成分に属さなければならない。□

この結果からは、任意の単純グラフはその成分の (より正確には、その成分に関する誘導部分グラフの) 非交和に分解できることが分かる。このとき各成分は連結なグラフである。また、容易に分かるように、単純グラフを連結なグラフの非交和に分解する方法はこれしか存在しない。

2.9.8接続性に関する練習問題

練習問題 2.11

\(G\) は単純グラフで \(\operatorname{V}\left( G\right) \neq\varnothing\) を満たすとする。次の二つの命題が同値であることを示せ:

  • 命題 1: \(G\) は連結である。

  • 命題 2: \(A\cap B=\varnothing\) と \(A\cup B=\operatorname{V}\left( G\right) \) を満たす \(\operatorname{V}\left( G\right) \) の任意の非空部分集合 \(A\), \(B\) に対して、\(ab\in\operatorname{E}\left( G\right) \) を満たす \(a \in A\) と \(b \in B\) が存在する。[言い換えれば: 連結な単純グラフ \(G\) の頂点集合 \(\operatorname{V}\left( G\right) \) を空でない部分集合二つに分けると、どのように分けたとしても、片方の部分集合に属する頂点ともう一方の部分集合に属する頂点を接続する辺が存在する。]

[解答: これは 2017 年春学期に開講された講義で出した homework set #1 の Exercise 7 である。解答は講義ページに載っている。]

練習問題 2.12

\(V\) を空でない有限集合、\(G\), \(H\) を \(\operatorname{V}\left( G\right) =\operatorname{V}\left( H\right) =V\) が成り立つ単純グラフとする。任意の \(u,v \in V\) に対して、\(u\) から \(v\) への \(G\) における路、または \(u\) から \(v\) への \(H\) における路が存在すると仮定する。このとき \(G\) と \(H\) の少なくとも一方が連結であることを示せ。

[解答: これは 2017 年春学期に開講された講義で出した homework set #1 の Exercise 8 である。解答は講義ページに載っている。]

練習問題 2.13

\(G=\left( V,E\right) \) を単純グラフとする。\(G\) の補グラフ (complement graph) \(\overline{G}\) は、単純グラフ \(\left( V,\ \mathcal{P}_{2}\left( V\right) \setminus E\right) \) と定義される。 [つまり、相異なる二頂点 \(u,v \in V\) は \(G\) で隣接していないとき、かつそのときに限って \(\overline{G}\) で隣接する。]

次の二つの命題の少なくとも一方が成り立つことを証明せよ:

  • 命題 1: 任意の \(u, v\in V\) に対して、\(u\) から \(v\) への長さが \(3\) 以下の路が \(G\) に存在する。

  • 命題 2: 任意の \(u, v\in V\) に対して、\(u\) から \(v\) への長さが \(2\) 以下の路が \(\overline{G}\) に存在する。

[解答: これは 2017 年春学期に開講された講義で出した homework set #1 の Exercise 9 である。解答は講義ページに載っている。]

練習問題 2.14

\(n \geq 2\) を整数、\(G\) を \(n\) 個の頂点を持つ連結なグラフとする。

  1. \(G\) の頂点の次数が \(1,1,2,2,\ldots,2\) (ちょうど \(2\) 個の \(1\) と、ちょうど \(n-2\) 個の \(2\)) のとき、\(G\) を描写せよ。

  2. \(G\) の頂点の次数が \(1,1,\ldots,1,n-1\) のとき、\(G\) を描写せよ。

  3. \(G\) の頂点の次数が \(2,2,\ldots,2\) のとき、\(G\) を描写せよ。

「\(G\) を描写する」とは、\(G\) と同型なグラフを (証明付きで) 明示的に示すことを意味する。

次の練習問題は接続性と成分を直接扱っているわけではないものの、成分に注目すると解きやすくなるだろう (成分を使わない解法もある)。

練習問題 2.15

\(G\) を \(n\) 個の頂点を持つ単純グラフとする。\(G\) の各頂点は少なくとも一つの隣接頂点を持つと仮定する。

\(G\) のマッチング (matching) とは、\(G\) の辺からなる集合 \(F\) であって任意の二要素が端点を共有しないものを言う。\(G\) のマッチングの最大要素数を \(m\) とする。

\(G\) の辺被覆 (edge cover) とは、\(G\) の辺からなる集合 \(F\) であって条件「\(G\) の全ての頂点がいずれかの \(e \in F\) に含まれる」を満たすものを言う。\(G\) の辺被覆の最小要素数を \(c\) とする。

\(m + c = n\) を示せ。

Remark 2.9.20

\(G\) を例 2.6.3 で定義した閉路グラフ \(C_{5}\) とする。このとき \(\left\{ 12,34\right\} \) は大きさが最大の \(G\) のマッチングである [なぜ？]。また、\(\left\{ 12,34,25\right\} \) は大きさが最小の \(G\) の辺被覆である [なぜ？]。練習問題 2.15 は \(m+c=2+3=5=n\) と主張しているが、これは確かに正しい。

  1. 正確に言うと: \(G\) の頂点数を \(n\) とするとき、このアルゴリズムの実行時間は \(n\) と \(k\) の多項式で抑えられる。 ↩︎

広告
このページの文章はテキストゆれないくんを使って校正されました。