5.6. 有向木
5.6.1 定義
無向グラフの話題は終わりにしよう。
向きが付いた木とはどんなものだろうか? つまり、どんな有向グラフが無向グラフにおける木と同じ役割を果たすだろうか?
無向グラフでは閉路を持たない連結なグラフを木と呼んだ。ここから「有向木」の定義が二つ示唆される:
-
閉路を持たない強連結な有向グラフを木と定義できそうに思える。しかし残念ながら、そういった有向グラフに関して議論できることは少ない: この条件を満たす任意の有向グラフは \(1\) 個の頂点と \(0\) 個の弧からなる (その理由を納得しておくこと!)。
-
連結性の条件を落としたらどうだろうか? 閉路を持たない有向グラフを非巡回 (acyclic) と言い、有向非巡回グラフ (directed acyclic graph) を DAG と呼ぶ。
しかし、DAG が木だとは言いにくい。例えば、無向グラフの木は「辺が頂点より少ない」という特徴を持つものの、DAG は頂点より多い弧を持つことができる1。
有向グラフにおける木の納得感ある定義は次の通りである:
\(D\) を多重有向グラフ、\(r\) を \(D\) の頂点とする。
-
\(D\) の各頂点 \(v\) に対して \(D\) が \(r\) から \(v\) への路を持つなら、\(r\) を始根 (from-root) と呼ぶ。始根は単に根 (root) とも呼ぶ。
-
\(r\) が始根であり、無向多重グラフ \(D^{\operatorname*{und}}\) が閉路を持たないとき、\(D\) は \(r\) を根とする有向木 (arborescence rooted from \(r\)) と呼ばれる。
もちろん終根 (to-root) と \(r\) を終根とする有向木 (arborescence rooted to \(r\)) の概念を考えることもできる。しかし、終根は弧の向きを反転させたグラフにおける始根なので、二つの概念を別々に考える必要はない。始根に関する性質を示せば、全ての弧の向きを反転させたグラフにおける終根の性質も示される。
次の多重有向グラフは \(0\), \(1\), \(2\) という三つの始根を持つ:
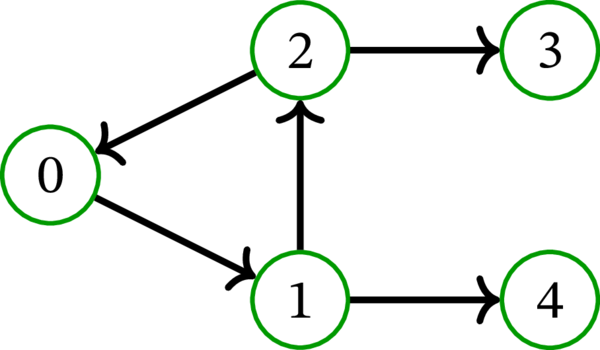
このグラフの弧を無向辺に入れ替えたグラフは閉路を持つので、このグラフは有向木ではない。
\(0\) から \(1\) への弧を反転させると、次の多重有向グラフが得られる:
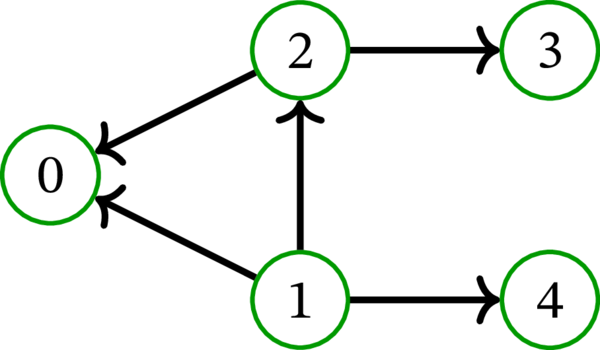
このグラフでは \(1\) だけが始根となる。このグラフも (同様の理由で) 有向グラフではない。
次の多重有向グラフを考える:
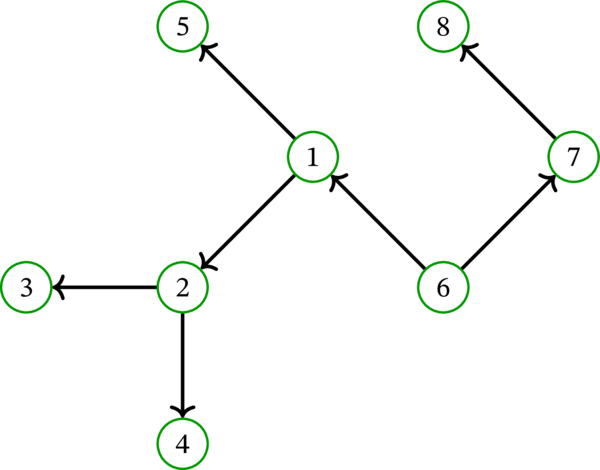
このグラフは \(6\) を根とする有向木である。実際、\(6\) から各頂点への路が存在し、弧を無向辺にすると木が得られる。
\(1\) から \(2\) への弧を反転させると次の多重有向グラフが得られる:
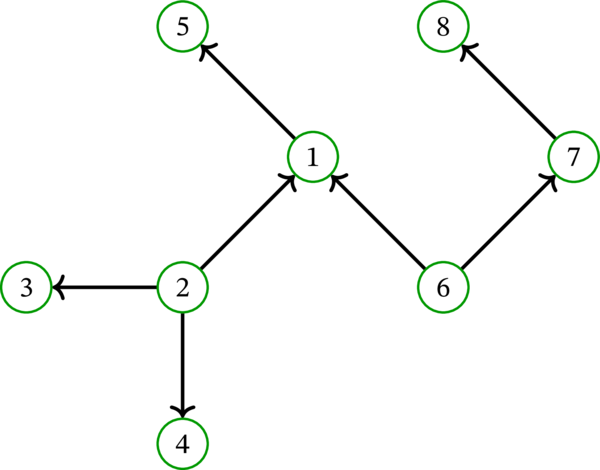
このグラフは始根を持たないので、有向木ではない。
5.6.2 有向木 vs. 木: 主張
上述の例からは、「\(r\) を根とする有向木」が「木の各辺に \(r\) から遠ざかるように向きをつけた木」と基本的に同じであることが示唆される。より正確に言えば次の通りである:
\(D\) を多重有向グラフ、\(r\) を \(D\) の頂点とする。このとき、次の二つの命題は同値である:
-
命題 C1: 多重有向グラフ \(D\) が \(r\) を根とする有向木である。
-
命題 C2: 無向多重グラフ \(D^{\operatorname*{und}}\) が木であり、\(D\) の各弧が \(r\) から遠ざかる向きを持つ (この意味は次の通りである: 任意の弧 \(e\) に対して、\(r\) から \(e\) の終点への路が \(e\) の始点を含む)。
この定理は簡単に理解できるものの、その厳密な証明は腹立たしいほど難しい! この定理の証明は後に回す。
5.6.3 有向木の同値性定理
木の同値性定理 (定理 5.2.4) に似た、有向木を特徴付ける一連の同値な条件を最初に示す:
\(D=\left( V,A,\psi\right) \) を多重有向グラフとする。\(D\) が始根 \(r\) を持つとき、次の六個の命題は同値である:
-
命題 A1: 多重有向グラフ \(D\) が \(r\) を根とする有向木である。
-
命題 A2: \(\left\vert A\right\vert =\left\vert V\right\vert -1\) が成り立つ。
-
命題 A3: 多重グラフ \(D^{\operatorname*{und}}\) が木である。
-
命題 A4: 各頂点 \(v \in V\) に対して、多重有向グラフ \(D\) に \(r\) から \(v\) への歩道が唯一つ存在する。
-
命題 A5: \(D\) から任意の弧を除去すると、頂点 \(r\) が (弧を除去した後のグラフにおいて) 始根でなくなる。
-
命題 A6: \(\deg^{-}r=0\) であり、全ての \(v\in V\setminus\left\{ r\right\} \) が \(\deg^{-}v=1\) を満たす。
これから A1\(\Longrightarrow\)A4\(\Longrightarrow \)A5\(\Longrightarrow\)A6\(\Longrightarrow\)A2\(\Longrightarrow\)A3\(\Longrightarrow \)A1 という論理関係を示す。つまり、六つの命題 A1\(\Longrightarrow\)A4, A4\(\Longrightarrow\)A5, ..., A3 \(\Longrightarrow\) A1 を一つずつ示す。これらの命題は一つの閉路を構成するから、全ての命題が同値であることを意味する。
証明の本筋に入る前に、記法を一つ定める: \(D\) の任意の弧 \(a\) に対して、\(D\) から弧 \(a\) を除去して得られるグラフを \(D \setminus a\) と表記する。[数学的に言えば
と定める。]
それでは六つの命題を証明していこう。
命題 A1 が成り立つと仮定する。このとき \(D\) は \(r\) を根とする有向木である。言い換えれば、\(r\) は \(D\) の始根であり、\(D^{\operatorname*{und}}\) は閉路を持たない。
各頂点 \(v \in V\) に対して、多重有向グラフ \(D\) に \(r\) から \(v\) への歩道が唯一つ存在すると示せばよい。\(r\) が \(D\) の始根なので、この歩道の存在は明らかである。よって後は唯一性を示す必要がある。
背理法で示す。\(r\) から \(v\) への異なる二つの歩道 \(\mathbf{u}\), \(\mathbf{v}\) が存在するような頂点 \(v\) が存在すると仮定する。\(D^{\operatorname*{und}}\) は閉路を持たないのでループを持たず、従って多重有向グラフ \(D\) もループを持たない。よって \(D\) の任意の歩道は自動的に \(D^{\operatorname*{und}}\) のバックトラックフリー歩道となる (有向グラフの歩道に含まれる連続する弧が同一なら、その弧はループである)。よって \(D\) における歩道 \(\mathbf{u}\) と \(\mathbf{v}\) は \(D^{\operatorname*{und}}\) における二つのバックトラックフリー歩道でもある。言い換えれば、\(D^{\operatorname*{und}}\) は \(r\) から \(v\) への二つの異なるバックトラックフリー歩道を持つ。よって定理 5.1.3 より \(D^{\operatorname*{und}}\) は閉路を持つと結論できる。しかし、これは \(D^{\operatorname*{und}}\) が閉路を持たない事実と矛盾する。
この矛盾は仮定が間違っていたことを示す。よって、各頂点 \(v\in V\) に対して \(D\) が \(r\) から \(v\) への路を唯一つ持つ。つまり命題 A4 は成り立つ。
命題 A4 が成り立つと仮定する。
\(D\) の任意の弧を \(a\) とする。多重有向グラフ \(D \setminus a\) で \(r\) が始根でないことを示せばよい。弧 \(a\) が始点 \(s\) と終点 \(t\) を持つとする。これから \(D\setminus a\) が \(r\) から \(t\) への路を持たないことを背理法で示す。
\(D \setminus a\) が \(r\) から \(t\) への路 \(\mathbf{p}\) を持つと仮定する。\(D\setminus a\) は弧 \(a\) を持たないので、\(\mathbf{p}\) は \(a\) を含まない。
一方、成り立つと仮定している命題 A4 で \(v=s\) とすると、多重有向グラフ \(D\) には \(r\) から \(s\) への歩道が唯一つ存在すると分かる。この歩道を \(\left( v_{0},a_{1},v_{1},a_{2},v_{2},\ldots,a_{k},v_{k}\right) \) とする。この歩道の末尾に弧 \(a\) と頂点 \(t\) を加えると、次の歩道が得られる:
これは \(r\) から \(t\) への歩道である。この歩道を \(\mathbf{q}\) とする。
\(\mathbf{p}\) と \(\mathbf{q}\) はどちらも \(D\) における \(r\) から \(t\) への歩道である。\(\mathbf{q}\) が弧 \(a\) を含むのに対して \(\mathbf{p}\) は含まないので、\(\mathbf{p}\) と \(\mathbf{q}\) は異なる。しかし、命題 A4 を \(v = t\) として適用すると、多重有向グラフ \(D\) は \(r\) から \(t\) への路を唯一つ持つことが分かる。これは \(\mathbf{p}\) と \(\mathbf{q}\) という二つの異なる歩道が \(D\) に存在する事実と矛盾する。
この矛盾から仮定が偽だと分かる。つまり \(D \setminus a\) には \(r\) から \(t\) への路が存在しない。よって \(r\) は \(D \setminus a\) の始根ではない。
\(a\) を固定したことを忘れる。以上の議論から、\(D\) の任意の弧 \(a\) に対して \(D \setminus a\) で \(r\) が始根でないことが証明された。言い換えれば、\(D\) から任意の弧を除去すると、\(r\) が (弧を除去した後のグラフにおいて) 始根でなくなる。つまり命題 A5 は成り立つ。
命題 A5 が成り立つと仮定する。命題 A6 を証明する必要がある。言い換えれば、\(\deg^{-}r=0\) であり、全ての \(v\in V\setminus\left\{ r\right\} \) が \(\deg^{-}v=1\) を満たすことを示せばよい。
最初に \(\deg^{-}r=0\) を背理法で示す。\(\deg^{-}r\neq0\) と仮定する。このとき \(r\) を終点とする弧 \(a\) が存在する。これから \(r\) が \(D \setminus a \) の始根だと示す。
\(r\) から始まる任意の路は終点が \(r\) の弧 \(a\) を含まない (路は同じ頂点を二度通れないため) ので、\(D\setminus a\) の路でもある。\(r\) は \(D\) の始根なので、\(D\) の任意の頂点 \(v\) に対して \(D\) は \(r\) から \(v\) への路を持つ。それらの路は \(D \setminus a\) の路でもあるので、\(D \setminus a\) の任意の頂点 \(v\) に対して \(D \setminus a\) は \(r\) から \(v\) への路を持つ。言い換えれば、\(r\) は \(D \setminus a\) の始根である。一方、成立を仮定した命題 A5 からは \(D \setminus a\) で \(r\) が始根でないと分かる。これは \(D \setminus a\) で \(r\) が始根である事実と矛盾する。
この矛盾から仮定が偽だと分かる。つまり \(\deg^{-} r = 0\) が証明された。
続いて \(v\in V\setminus\left\{ r\right\} \) を任意に取る。\(\deg^{-}v=1\) を示す必要がある。
背理法で示す。\(\deg^{-}v\neq1\) と仮定する。\(r\) が \(D\) の始根より \(\deg^{-}v\geq 2\) が分かる3。よって終点が \(v\) の異なる二つの弧 \(a\), \(b\) が存在する。
続いて、三つの場合を分けて考える:
-
Case 1: 有向グラフ \(D \setminus a\) が \(r\) から \(v\) への路を持つ。
-
Case 2: 有向グラフ \(D \setminus b\) が \(r\) から \(v\) への路を持つ。
-
Case 3: 有向グラフ \(D\setminus a\) と有向グラフ \(D\setminus b\) がどちらも \(r\) から \(v\) への路を持たない。
まず Case 1 を考える。このとき有向グラフ \(D \setminus a\) は \(r\) から \(v\) への路 \(\mathbf{p}\) を持つ。
成立を仮定した命題 A5 より、\(D\) から弧 \(a\) を除去した \(D \setminus a\) で \(r\) は始根でなくなる。始根の定義を使って言い換えれば、有向グラフ \(D \setminus a\) が \(r\) から \(w\) への路を持たないような頂点 \(w \in V\) が存在する。
\(r\) は有向グラフ \(D\) の始根より、\(D\) は \(r\) から \(w\) への路 \(\mathbf{q}\) を持つ。この路 \(\mathbf{q}\) に注目する。もし \(\mathbf{q}\) が弧 \(a\) を含まないなら、\(\mathbf{q}\) は \(D \setminus a\) の路にもなる。しかし \(D \setminus a \) は \(r\) から \(w\) への路を持たないので、これはあり得ない。よって路 \(\mathbf{q}\) は弧 \(a\) を含む。
\(\mathbf{q}\) の弧 \(a\) より後の部分を考える。この部分は \(v\) から \(w\) への路である (\(a\) の終点は \(v\) で、\(\mathbf{q}\) の終点は \(w\) であるため)。この路を \(\mathbf{q}^{\prime}\) とすれば、\(\mathbf{q}\) が路なので \(\mathbf{q}^{\prime}\) は \(a\) を含まない。よって \(\mathbf{q}^{\prime}\) は \(D \setminus a\) の路である。
よって有向グラフ \(D \setminus a\) は \(r\) から \(v\) への路 \(\mathbf{p}\) と \(v\) から \(w\) への路 \(\mathbf{q}^{\prime}\) を持つ。二つの路を連結すれば、\(r\) から \(w\) への歩道 \(\mathbf{p}\ast\mathbf{q}^{\prime}\) を得る。つまり \(D \setminus a\) は \(r\) から \(w\) への歩道を持つ。よって系 3.3.10 より、\(D \setminus a\) は \(r\) から \(w\) への路を持つと結論できる。これは \(D \setminus a\) が \(r\) から \(w\) への路を持たない事実と矛盾する。
よって Case 1 で矛盾が導けた。
この議論の \(a\) を \(b\) に置き換えれば、Case 2 でも同様に矛盾が導ける。
最後に Case 3 を考える。このとき有向グラフ \(D \setminus a\) と有向グラフ \(D \setminus b\) がどちらも \(r\) から \(v\) への路を持たない。一方、\(r\) は有向グラフ \(D\) の始根より \(D\) は \(r\) から \(v\) への路 \(\mathbf{p}\) を持つ。仮に \(\mathbf{p}\) が弧 \(a\) を含まないなら、\(\mathbf{p}\) は \(D \setminus a\) における \(r\) から \(v\) への路にもなって仮定に反する。よって \(\mathbf{p}\) は \(a\) を含む。同様の議論から \(\mathbf{p}\) は \(b\) を含むことも分かる。しかし、二つの弧 \(a\), \(b\) は同じ終点 \(v\) を持つので、一つの路が \(a\) と \(b\) の両方を含むことはない (路は同じ頂点を最大でも一度しか含まないため)。これは \(\mathbf{p}\) が \(a\) と \(b\) の両方を含む事実と矛盾する。以上で Case 3 でも矛盾が導けた。
Case 1, Case 2, Case 3 のそれぞれで矛盾を導いたので、仮定が偽だと分かる。よって \(\deg^{-}v=1\) が証明された。
以上で任意の \(v\in V\setminus\left\{ r\right\} \) が \(\deg^{-}v=1\) を満たすことが示せた。\(\deg^{-}r=0\) は前に示したので、これで命題 A6 の証明が完了した。
命題 A6 が成り立つと仮定する。命題 A2 が成り立つことを示せばよい。命題 4.2.3 から次の等式が分かる:
よって命題 A2 は成り立つ。
命題 A2 が成り立つと仮定する。命題 A3 が成り立つことを示せばよい。
頂点 \(r\) は有向グラフ \(D\) の始根なので、任意の \(v \in V\) に対して \(D\) は \(r\) から \(v\) への路を持つ。よって \(v \in V\) を \(D\) の任意の頂点とするとき、グラフ \(D^{\operatorname*{und}}\) は \(r\) から \(v\) への路を持つ (\(D\) の任意の路は \(D^{\operatorname*{und}}\) の路であるため)。ここから \(D^{\operatorname*{und}}\) の任意の二頂点 \(u\), \(v\) が路連結だと分かる (\(r\) を経由すれば \(u\) から \(v\) に行けるため)。つまり、\(D^{\operatorname*{und}}\) は連結である (\(D^{\operatorname*{und}}\) は少なくとも一つの頂点を持つ4ため)。さらに、命題 A2 より \(D^{\operatorname*{und}}\) の辺の個数が \(\left\vert A\right\vert =\left\vert V\right\vert -1\) だと分かる。以上より、多重グラフ \(D^{\operatorname*{und}}\) は木の同値性定理 (定理 5.2.4) の命題 T4 を満たす。よって \(D^{\operatorname*{und}}\) は命題 T1 も満たす: つまり木である。これで命題 A3 は証明された。
命題 A3 が成り立つと仮定する。命題 A1 が成り立つと示せばよい。
命題 A3 より多重グラフ \(D^{\operatorname*{und}}\) は木なので、森でもある。つまり閉路を持たない。頂点 \(r\) が有向グラフ \(D\) の始根であることも分かっているので、有向木の定義より \(D\) は \(r\) を根とする有向木である。言い換えれば命題 A1 が成り立つ。
以上で A1\(\Longrightarrow\)A4\(\Longrightarrow\)A5\(\Longrightarrow\)A6\(\Longrightarrow \)A2\(\Longrightarrow\)A3\(\Longrightarrow\)A1 が全て示せた。よって命題 A1, A2, ..., A6 は同値である。以上で定理 5.6.5 は証明された。□
閉路5を持たない多重有向グラフを \(D=\left( V,A,\phi\right) \) とする。\(r \in V\) を \(D\) の頂点とするとき、次の命題を示せ:
-
全ての \(u \in V \setminus \left\{ r \right\} \) で \(\deg^{-} u > 0\) が成り立つなら、\(r\) は \(D\) の始根である。
-
全ての \(u\in V\setminus\left\{ r\right\} \) で \(\deg^{-}u=1\) が成り立つなら、\(D\) は \(r\) を根とする有向木である。
-
例えば、次の DAG は \(4\) 個の頂点と \(5\) 個の弧を持つ:
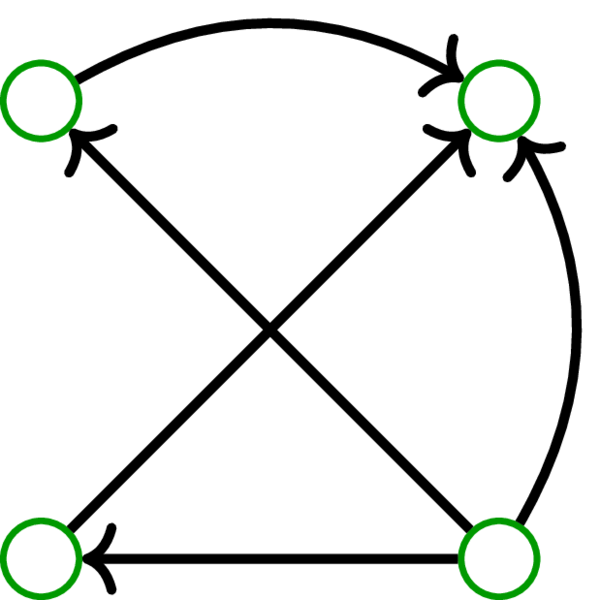
-
任意の多重有向グラフ \(D\) に対する \(D^{\operatorname*{und}}\) は定義 4.4.1 で定義した。大まかに言えば、多重グラフ \(D^{\operatorname*{und}}\) は \(D\) の弧が持つ向きを「無視」することで得られる (平行辺はそのままとする)。例えば \(D = \)
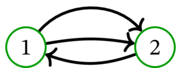 なら \(D^{\operatorname*{und}} = \)
なら \(D^{\operatorname*{und}} = \) 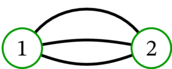 となる。 ↩︎
となる。 ↩︎ -
証明: \(r\) が \(D\) の始根なので、有向グラフ \(D\) は \(r\) から \(v\) への路を持つ。\(v\in V\setminus\left\{ r\right\} \) より \(v \neq r\) だから、この路は少なくとも一つの弧を含む。この路の最後の弧は明らかに \(v\) を終点に持つ。つまり \(\deg^{-}v\geq1\) である。これと仮定の \(\deg^{-}v\neq1\) を組み合わせれば \(\deg^{-}v\geq2\) を得る。 ↩︎
-
\(r \in V\) から分かる。 ↩︎
-
有向グラフの閉路は向きが付いている必要がある点に注意してほしい ── 各弧を始点から終点に向かってたどらなければならない。 ↩︎