5.7. 有向木 vs. 木
続いて有向木と木を関連付ける定理 5.6.4 を証明する。
厳密な証明を行うには、木に関する新しい記法をいくつか導入する必要がある。まず、木において距離 (定義 5.5.1) が持つ性質を一つ証明する:
\(T\) を木、\(r\) を \(T\) の頂点、\(e\) を \(T\) の辺、\(u\), \(v\) を \(e\) の端点とするとき \(d\left( r,u\right) \) と \(d\left( r,v\right) \) はちょうど \(1\) だけ異なる。言い換えれば、\(d\left( r,u\right) =d\left( r,v\right) +1\) または \(d\left( r,v\right) =d\left( r,u\right) +1\) が成り立つ。
\(T\) は木なので、\(T\) の二頂点 \(p\), \(q\) 間の距離 \(d\left( p,q\right) \) は \(T\) における \(p\) から \(q\) への唯一の路の長さに等しい。
\(r\) から \(u\) への唯一の路を \(\mathbf{p}\) とする。このとき、次の二つの場合が考えられる:
-
Case 1: 辺 \(e\) が \(\mathbf{p}\) に含まれる。
-
Case 2: 辺 \(e\) が \(\mathbf{p}\) に含まれない。
Case 1 を考える。辺 \(e\) が \(\mathbf{p}\) に含まれるとき \(e\) は \(\mathbf{p}\) の最後の辺でなければならない (路である \(\mathbf{p}\) は終点 \(u\) に一度だけ訪れるため)。よって辺 \(e\) (と頂点 \(u\)) を \(\mathbf{p}\) から除去すると、\(r\) から \(v\) への路が得られる。この路の長さは \(\mathbf{p}\) の長さより \(1\) だけ小さいので、\(d\left( r,v\right) =d\left( r,u\right) -1\) つまり \(d\left( r,u\right) =d\left( r,v\right) +1\) が分かる。これで Case 1 における証明が完了した。
続いて Case 2 を考える。辺 \(e\) が \(\mathbf{p}\) に含まれないので、\(\mathbf{p}\) の末尾に辺 \(e\) と頂点 \(v\) を末尾に追加した \(\mathbf{p}^{\prime}\) はバックトラックフリー歩道となる。木においてバックトラックフリー歩道は路となる (そうでなければ命題 5.1.2 より閉路が生じてしまう) ので、\(\mathbf{p}^{\prime}\) は \(r\) から \(v\) への路である。\(\mathbf{p}^{\prime}\) の長さは \(\mathbf{p}\) の長さより \(1\) だけ大きいので \(d\left( r,v\right) =d\left( r,u\right) +1\) が分かる。以上で Case 2 における証明が完了した。
両方の場合で証明できたので、命題 5.7.1 は証明された。□
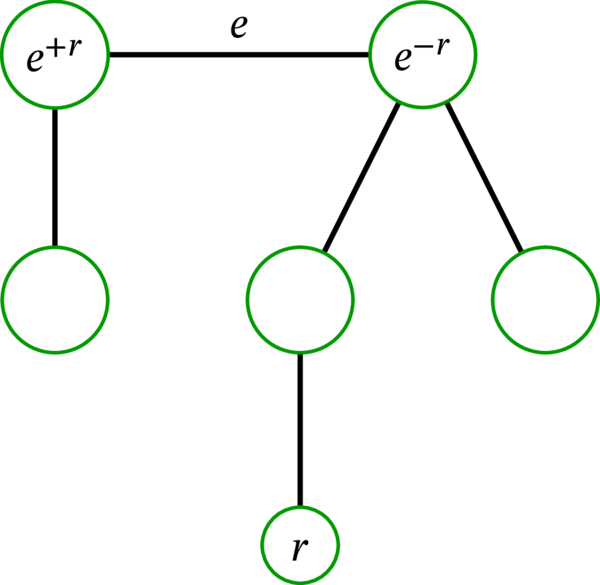
\(T\) を木、\(r\) を \(T\) の頂点、\(e\) を \(T\) の辺とする。命題 5.7.1 より、\(e\) の両端点と \(r\) の距離はちょうど \(1\) だけ異なる。言い換えれば、どちらかがもう一方より \(1\) だけ小さい。
-
\(r\) との距離が小さい方の \(e\) の端点を \(e\) の \(r\)-親 (\(r\)-parent) と呼び、\(e^{-r}\) と表記する。
-
\(r\) との距離が大きい方の \(e\) の端点を \(e\) の \(r\)-子 (\(r\)-child) と呼び、\(e^{+r}\) と表記する。
このとき命題 5.7.1 から次の等式が分かる:
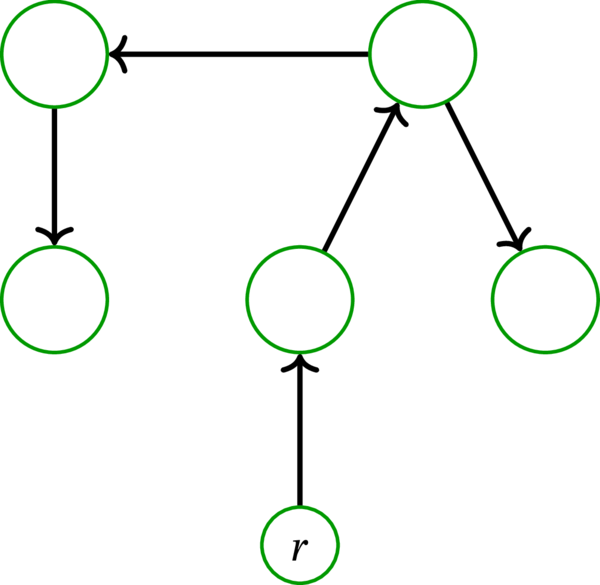
\(T=\left( V,E,\varphi\right) \) を木、\(r\) を \(T\) の頂点とする。多重グラフ \(T^{r\rightarrow}\) を次のように定める:
ここで写像 \(\psi\colon E\rightarrow V\times V\) は辺 \(e \in E\) を組 \(\left( e^{-r},e^{+r}\right) \in V \times V \) に移す。数学的でない言葉で言えば、\(T\) の各辺 \(e\) を \(r\)-親 \(e^{-r}\) から \(r\)-子 \(e^{+r}\) への弧に変えることで得られる多重有向グラフが \(T^{r\rightarrow}\) と言える。定理 5.6.4 の導入で「各辺に \(r\) から遠ざかるように向きを付けた木」と言ったときに意味していたのがこの多重有向グラフである。
この記法を使うと、定理 5.6.4 は次のように書き換えられる:
\(D\) を多重有向グラフ、\(r\) を \(D\) の頂点とする。このとき次の二つの命題は同値である:
-
命題 C1: 多重有向グラフ \(D\) が \(r\) を根とする有向木である。
-
命題 C2: 無向多重グラフ \(D^{\operatorname*{und}}\) が木であり、\(D=\left( D^{\operatorname*{und}}\right) ^{r\rightarrow}\) が成り立つ。
この定理の証明では二つの補題を利用する:
\(T=\left( V,E,\varphi\right) \) を木、\(r \in V\) を \(T\) の頂点とする。多重有向グラフ \(T^{r\rightarrow}\) は \(r\) を根とする有向木である。
「木 \(T\) における \(r\) から任意の頂点 \(v\) への路を \(\mathbf{p}\) とするとき、\(\mathbf{p}\) は有向グラフ \(T^{r\rightarrow}\) の路でもある」ことを示すのが基本的なアイデアとなる。これは、\(\mathbf{p}\) の各辺が \(T^{r\rightarrow}\) で「正しく」 (\(\mathbf{p}\) を進むときと同じ方向に) 向き付けられている事実から分かる。
詳しい証明を示す: 明らかに \(\left( T^{r\rightarrow}\right) ^{\operatorname*{und}}=T\) なので、グラフ \(\left( T^{r\rightarrow}\right) ^{\operatorname*{und}}\) は木であり閉路を持たない。よって後は \(r\) が \(T^{r\rightarrow}\) の始根だと示せばよい。言い換えれば、次の命題を示す必要がある:
これから \(d\left( r,v\right) \) に関する数学的帰納法で命題 \((1)\) を示す。ここで \(d\) は木 \(T\) における距離を表す。
ベースケース: \(v \in V\) が \(d\left( r,v\right) =0\) を満たすなら \(v = r\) であり、\(T^{r\rightarrow}\) は \(r\) から \(v\) への自明な路 \(\left( r\right) \) を持つ。よって命題 \((1)\) は \(d\left( r,v\right) =0\) のとき成り立つ。
再帰ステップ: \(k \in \mathbb{N}\) を任意に取る。\(d\left( r,v\right) =k\) を満たす全ての \(v \in V\) に対して命題 \((1)\) が成り立つと (帰納法の仮定として) 仮定する。
\(d\left( r,v\right) =k+1\) を満たす \(v \in V\) を任意に取る。このとき木 \(T\) における \(r\) から \(v\) への唯一の路を \(\mathbf{p}\) とすると、\(\mathbf{p}\) の長さは \(k + 1\) である。\(e\) を \(\mathbf{p}\) の最後の辺、\(u\) を \(\mathbf{p}\) の最後から二番目の頂点とする (このとき \(e\) の端点は \(u\) と \(v\) である)。\(\mathbf{p}\) から最後の辺 \(e\) を除去すると、\(r\) から \(u\) への (唯一の) 路が得られる。この路は \(\mathbf{p}\) より一つだけ少ない辺を持つので、\(d\left( r,u\right) =d\left( r,v\right) -1 < d\left( r,v\right) \) が成り立つ。よって辺 \(e\) の \(r\)-親は \(u\) であり、\(r\)-子は \(v\) だと分かる (定義 5.7.2 より)。言い換えれば \(e^{-r}=u\) および \(e^{+r}=v\) である。つまり有向グラフ \(T^{r\rightarrow}\) で辺 \(e\) は \(u\) から \(v\) への弧となる (定義 5.7.4 より)。さらに \(d\left( r,v\right) =k+1\) から \(d\left( r,u\right) =d\left( r,v\right) -1=k\) が分かるので、帰納法の仮定から命題 \((1)\) が \(u\) に対して成り立つことが分かる。言い換えれば、\(T^{r\rightarrow}\) は \(r\) から \(u\) への路を持つ。この路の最後に弧 \(e\) と頂点 \(v\) を加えれば、\(T^{r\rightarrow}\) における \(r\) から \(v\) への歩道が得られる (\(T^{r\rightarrow}\) で \(e\) は \(u\) から \(v\) への弧であるため)。有向グラフ \(T^{r\rightarrow}\) は \(r\) から \(v\) への歩道を持つので、\(r\) から \(v\) への路も持つ。つまり \(v\) に対して命題 \((1)\) は成り立つ。以上で再帰ステップが完了した。
よって数学的帰納法より命題 \((1)\) が示された。先述の通り、これで補題 5.7.7 は証明された。□
\(r \in V\) を根とする有向木を \(D=\left( V,A,\psi\right) \) とする。\(D\) の弧 \(a \in A\) を任意に取り、\(a\) の始点を \(s\) として、\(a\) の終点を \(t\) とする。このとき:
-
\(d\left( r,s\right) < d\left( r,t\right) \) が成り立つ。ここで \(d\) は木 \(D^{\operatorname*{und}}\) における距離を表す。
-
多重有向グラフ \(\left( D^{\operatorname*{und}}\right) ^{r\rightarrow}\) において、弧 \(a\) は始点 \(s\) と終点 \(t\) を持つ。
(a): \(D\) が \(r\) を根とする有向木なので、頂点 \(r\) は \(D\) の始根である。よって \(D\) は \(r\) から \(t\) への路を持つ。この路を \(\mathbf{p}\) とする。\(\mathbf{p}\) の最後の弧 \(a\) の終点が \(t\) なので、\(\deg^{-}t\geq1\) が成り立つ。
有向グラフ \(D\) は \(r\) を根とする有向木なので、有向木の同値性定理 (定理 5.6.5) の命題 A6 を満たす。つまり次の命題が成り立つ:
特に、ここから任意の \(v\in V\) に対して \(\deg^{-}v\leq1\) だと分かる。\(v = t\) とすれば \(\deg^{-}t\leq1\) を得る。これと \(\deg^{-}t\geq 1\) から \(\deg^{-}t = 1\) であり、弧 \(a\) は \(t\) を終点に持つ唯一の弧だと結論できる。
\(\deg^{-}r=0\) と \(\deg^{-}t \geq 1 > 0\) より \(t \neq r\) が分かる。よって \(r\) から \(t\) への路 \(\mathbf{p}\) は少なくとも一つの弧を含む。\(\mathbf{p}\) の最後の弧は終点が \(t\) なので、\(a\) である (終点が \(t\) の弧は \(a\) しか存在しないため)。
路 \(\mathbf{p}\) から最後の弧 \(a\) を除去すると、\(r\) から \(s\) への路 \(\mathbf{p}^{\prime}\) が得られる (\(a\) の始点が \(s\) であるため)。
一方、\(D\) の路は \(D^{\operatorname*{und}}\) の路でもある。よって特に、\(\mathbf{p}\) は \(D^{\operatorname*{und}}\) における \(r\) から \(t\) への路であり、\(\mathbf{p}^{\prime}\) は \(D^{\operatorname*{und}}\) における \(r\) から \(s\) への路である。\(\mathbf{p}^{\prime}\) の長さは \(\mathbf{p}\) の長さより \(1\) だけ小さいので、\(d\left( r,s\right) =d\left( r,t\right) -1 < d\left( r,t\right) \) を得る。これで補題 5.7.8 (a) は証明された。
(b): 有向グラフ \(D\) の弧 \(a\) は始点 \(s\) と終点 \(t\) を持つ。よって木 \(D^{\operatorname*{und}}\) の辺 \(a\) は \(s\) と \(t\) を端点に持つ。(a) より \(d\left( r,s\right) < d\left( r,t\right) \) だから、\(D^{\operatorname*{und}}\) における \(a\) の \(r\)-親は \(s\) で、\(D^{\operatorname*{und}}\) における \(a\) の \(r\)-子が \(t\) だと分かる (定義 5.7.2 より)。よって有向グラフ \(\left( D^{\operatorname*{und}}\right) ^{r\rightarrow}\) で \(a\) は始点 \(s\) と終点 \(t\) を持つ (定義 5.7.4 より)。以上で補題 5.7.8 (b) は証明された。□
多重有向グラフ \(D\) を \(D=\left( V,A,\psi\right) \) と書く。C1 \(\Longrightarrow\) C2 と C2 \(\Longrightarrow\) C1 を別々に証明する。
命題 C1 が成り立つと仮定する。つまり、\(D\) は \(r\) を根とする有向木とする。命題 C2 を証明する必要がある。言い換えれば、無向多重グラフ \(D^{\operatorname*{und}}\) が木であること、そして \(D=\left( D^{\operatorname*{und}}\right) ^{r\rightarrow}\) が成り立つことを示せばよい。
\(D^{\operatorname*{und}}\) が木であることは有向木の定義より明らかなので、これから \(D=\left( D^{\operatorname*{und}}\right) ^{r\rightarrow}\) を示す。
多重有向グラフ \(D\) と \(\left( D^{\operatorname*{und}}\right) ^{r\rightarrow}\) はどちらも頂点集合 \(V\) と弧集合 \(A\) を持つので、後は \(\left( D^{\operatorname*{und}}\right) ^{r\rightarrow} = \left(V, A, \psi^{\prime}\right)\) を満たす写像 \(\psi^{\prime}\) に対して \(\psi = \psi^{\prime}\) が示せれば \(D = \left( D^{\operatorname*{und}}\right) ^{r\rightarrow}\) が証明される。
\(a \in A\) を任意に取って \(\psi\left( a\right) =\left( s,t\right) \) とする。つまり、\(D\) で弧 \(a\) は始点 \(s\) と終点 \(t\) を持つ。このとき補題 5.7.8 (b) より、多重有向グラフ \(\left( D^{\operatorname*{und}}\right) ^{r\rightarrow}\) でも弧 \(a\) は始点 \(s\) と終点 \(t\) を持つ。言い換えれば \(\psi^{\prime }\left( a\right) =\left( s,t\right) \) である。よって \(\psi^{\prime}\left( a\right) =\left( s,t\right) =\psi\left( a\right) \) が分かる。
\(a\) を固定したことを忘れる。以上で任意の \(a \in A\) で \(\psi^{\prime}\left( a\right) =\psi\left( a\right) \) だと証明できた。言い換えれば \(\psi^{\prime}=\psi\) である。先述したように、これで命題 C2 の証明が完了した。
命題 C2 が成り立つと仮定する。つまり、無向多重グラフ \(D^{\operatorname*{und}}\) が木であり、\(D=\left( D^{\operatorname*{und}}\right) ^{r\rightarrow}\) だとする。\(D^{\operatorname*{und}}\) に補題 5.7.7 を適用すると、多重有向グラフ \(\left( D^{\operatorname*{und}}\right) ^{r\rightarrow}\) が \(r\) を根とする有向木だと分かる。よって \(D=\left( D^{\operatorname*{und}}\right) ^{r\rightarrow}\) より \(D\) は \(r\) を根とする有向木である。以上で命題 C1 が成り立つことが示せた。
C1 \(\Longrightarrow\) C2 と C2 \(\Longrightarrow\) C1 の両方が証明できたので、命題 C1 と命題 C2 は同値である。以上で定理 5.7.6 は証明された。□
ふぅ。
この定理を使って命題をいくつか証明しておこう。まず、有向木に根は一つしか存在しない:
\(D\) を \(r\) を根とする有向木とする。このとき \(r\) は \(D\) が持つ唯一の根である。
背理法で示す。\(D\) が \(r\) と異なる根 \(s\) を持つと仮定する。このとき \(D\) は (\(r\) が根なので) \(r\) から \(s\) への路を持ち、さらに (\(s\) が根なので) \(s\) から \(r\) への路も持つ。この二つの路を連結すると、長さが \(1\) より大きい閉歩道が得られる。閉歩道は明らかに路でないので、命題 4.5.9 より \(D\) が閉路を持つことが分かる。よって \(D^{\operatorname*{und}}\) も閉路を持つ (\(D\) の閉路は \(D^{\operatorname*{und}}\) の閉路でもあるため)。一方 \(D\) は \(r\) を根とする有向木なので、\(D^{\operatorname*{und}}\) は閉路を持たない。両者は矛盾するので、仮定が偽だと分かる。これで命題 5.7.8 は証明された。□
\(D\) を多重有向グラフとする。ある頂点 \(r\) が存在して \(D\) が \(r\) を根とする有向木であるとき、\(D\) を有向木 (arborescence) と呼ぶ。命題 5.7.8 より、\(D\) が有向木のとき \(D\) の根は一意に定まる。
次の二つの写像 \(\psi_{1}\), \(\psi_{2}\) はお互いがもう一方の逆写像である:
ここで \(\sqrt{D}\) は \(D\) の根を表す。
写像 \(\psi_{1}\) は補題 5.7.7 より well-defined である。また、\(D\) が有向木のとき \(D^{\operatorname*{und}}\) が木である事実から写像 \(\psi_{2}\) は well-defined である。後は次の二つの命題を示せばよい:
-
有向木 \(D\) は \(\left( D^{\operatorname*{und}}\right) ^{r\rightarrow}=D\) を満たす。ここで \(r\) は \(D\) の根を表す。
-
木 \(T\) と \(T\) の頂点 \(r\) の組 \(\left( T,r\right) \) のそれぞれが \(\left( T^{r\rightarrow}\right) ^{\operatorname*{und}}=T\) と \(\sqrt{T^{r\rightarrow}}=r\) を満たす。
一つ目の命題は定理 5.7.6 (の C1 \(\Longrightarrow\) C2) から従う。二つ目の命題は補題 5.7.7 から従う (詳しく言えば、\(\left( T^{r\rightarrow }\right) ^{\operatorname*{und}}=T\) は明らかであり、\(\sqrt{T^{r\rightarrow}}=r\) が補題 5.7.7 から従う)。よって定理 5.7.10 は証明された。□
定理 5.7.10 は有向木が「頂点の一つに印が付いた木」に過ぎないというアイデアを数学的に表現したものと言える。このため有向木は (英語で) arborescence ではなく oriented tree (向きが付いた木) と呼ばれることもある。ただ、木に向きを付けた任意の有向グラフを oriented tree と呼ぶこともあるので、本書では oriented tree という単語を使用しない。
連結な多重グラフ \(G=\left( V,E,\varphi\right) \) が \(\left\vert E\right\vert \geq\left\vert V\right\vert \) を満たすと仮定する。任意の頂点 \(v \in V\) が辺 \(f\left( v\right) \) に含まれるような単射 \(f\colon V\rightarrow E\) が存在することを示せ。