5.5. グラフと木の中心

5.5.1距離

グラフが与えられたとき、二つの頂点の間に「距離」を定義できる。距離は二頂点を結ぶ最短路が持つ辺の個数を表す:

[証明] (d) は系 3.3.10 から従う。(a), (b), (c) は明らかである。 [(c) の証明では (d) が利用できる。] 最後に、(e) は多重グラフが持つ任意の路の長さが \(\left\vert V\right\vert -1\) 以下である事実から分かる (路の頂点は相異なるため)。□

考えている多重グラフが木のとき距離の定義は単純になることを指摘しておく。木 \(T\) において二頂点 \(u\), \(v\) 間の距離 \(d\left( u,v\right) \) は \(T\) における \(u\) から \(v\) への唯一の路の長さに等しい。つまり、木では路が最短かどうかを考慮する必要がない。

また、次の事実も分かる: \(G\) を多重グラフ、\(u\), \(v\) を \(G\) の二頂点とするとき、\(G\) における距離 \(d_{G}\left( u,v\right) \) は単純グラフ \(G^{\operatorname*{simp}}\) における距離 \(d_{G^{\operatorname*{simp}}}\left( u,v\right) \) に等しい。\(G\) における任意の路に対応して同じ長さの \(G^{\operatorname*{simp}}\) における路が存在し、逆も成り立つためである。当然この対応関係は一対一ではないものの、距離が等しいことは言える。そのためグラフの距離を議論するときは、単純グラフだけを考えても一般性は失われない。

様々なグラフにおける距離が持つ興味深い特徴に関する練習問題をいくつか示す:

5.5.2離心率と中心

続いて離心率と呼ばれる値を定義する:

[グラフの中心に少しだけ違う定義を使う文献もある: そういった文献では、離心率が最小となる \(G\) の頂点の集合を中心と呼ぶ。この「中心」は本書が「中心」と呼ぶ頂点全体からなる集合に等しい。]

例 5.5.6

\(G\) を次の多重グラフとする:

このとき、各頂点の離心率は次の通りである:

この図から、\(G\) の中心が \(r\) と \(v\) だと分かる。

5.5.3木の中心の性質

例 5.5.8 から分かるように、離心率と中心はグラフが連結でないときあまり考える意味がない。さらに例 5.5.6 からは、グラフが連結だったとしても中心同士が隣接するとは限らないことが分かる。しかし木においては、離心率と中心が優れた性質を持つ:

定理 5.5.9 を証明するには、木から全ての葉を除去する操作に関する次の補題を示す必要がある:

例 5.5.11

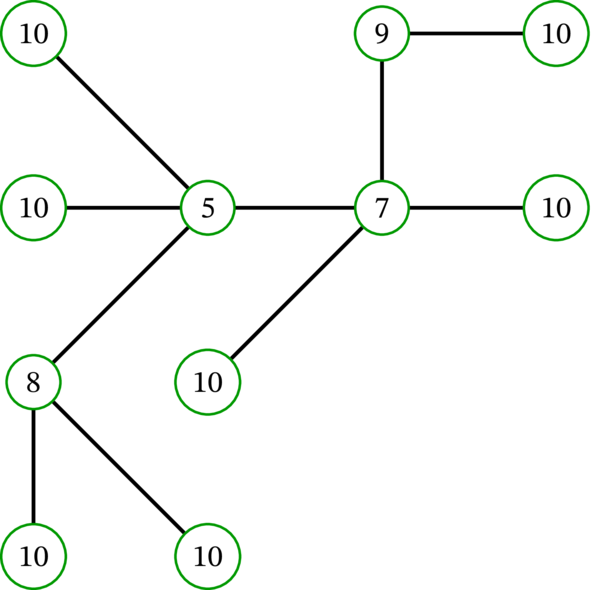
\(T\) を次の木とする:

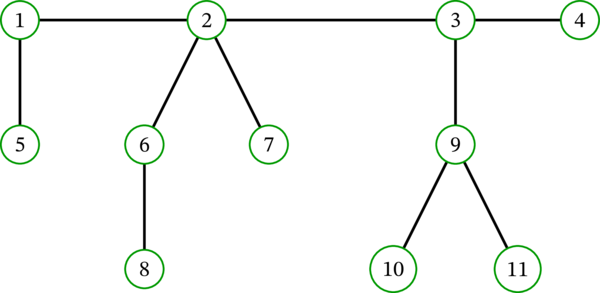
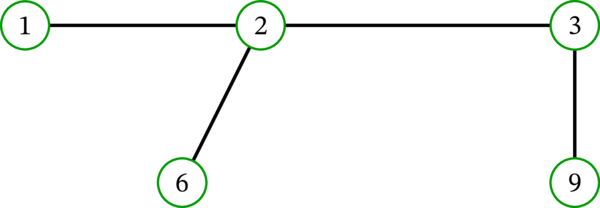
このとき補題 5.5.10 における集合 \(L\) は \(\left\{ 4,5,7,8,10,11\right\} \) であり、木 \(T\setminus L\) は次のグラフとなる:

[補題 5.5.10 の証明] 木である \(T\) は森なので、閉路を持たない。特に \(T\) はループと平行辺を持たない。また、\(T\) の任意の二頂点 \(u\), \(v\) に対して \(T\) には \(u\) から \(v\) への路が唯一つ存在する。

続いて用語を一つ定義する: 多重グラフの路 \(\mathbf{p}\) の内部頂点 (intermediate vertex) とは、始点でも終点でもない \(\mathbf{p}\) の頂点を言う。言い換えれば、多重グラフの路 \(\left( p_{0},e_{1},p_{1},e_{2},p_{2},\ldots,e_{k},p_{k}\right) \) の内部頂点は \(p_{1},p_{2},\ldots ,p_{k-1}\) である。明らかに、路 \(\mathbf{p}\) の内部頂点は \(2\) より大きい次数を持つ (\(\mathbf{p}\) は何らかの辺を通じて内部頂点に到達し、それとは別の辺を通じて内部頂点を離れるため)。よって \(T\) の任意の路 \(\mathbf{p}\) に対して次の命題が成り立つ:

[\(\mathbf{p}\) の内部頂点は \(2\) 以上の次数を持つので \(T\) の葉ではなく、従って \(L\) に属さず \(V\setminus L\) に属するため。]

(b): 任意に \(u, v\in V\setminus L\) を取る。\(T\) における \(u\) から \(v\) への路を \(\mathbf{p}\) として、これから \(\mathbf{p}\) が \(T \setminus L\) でも路だと示す。

まず \(\mathbf{p}\) の頂点が全て \(V \setminus L\) に属すると示す。\(u, v\in V\setminus L\) より \(u\) と \(v\) に対しては明らかであり、\(\mathbf{p}\) の中間頂点に対しても命題 \((1)\) より成り立つ。よって \(\mathbf{p}\) の全ての頂点は \(V \setminus L\) に属する。

\(T\setminus L\) は集合 \(V\setminus L\) に関する \(T\) の誘導部分多重グラフなので、\(\mathbf{p}\) の頂点が全て \(V \setminus L\) に属する事実から \(\mathbf{p}\) が \(T \setminus L\) における路でもあることが分かる。

\(\mathbf{p}\) を固定したことを忘れる。以上で \(T\) における \(u\) から \(v\) への路が \(T \setminus L\) における路でもあることが証明できた。よって次の関係が成り立つ:

\(T \setminus L\) は \(T\) の部分多重グラフなので、\(T \setminus L\) における任意の路は \(T\) における路でもある。よって次に示す逆の関係も成り立つ:

二つの関係をまとめれば次の関係を得る:

以上で補題 5.5.10 (b) は証明された。

(c): (b) から従う。なぜなら、グラフ \(G\) の二頂点 \(u\), \(v\) 間の距離 \(d_{G}\left( u,v\right) \) は \(u\) から \(v\) への最短路の長さとして定義されるからである。

(a): 木である \(T\) は森なので、部分多重グラフ \(T\setminus L\) も森だと分かる (\(T\setminus L\) の閉路は \(T\) の閉路にもなってしまう)。後は \(T\setminus L\) が連結だと示せばよい。

まず、\(T\setminus L\) は明らかに少なくとも一つの頂点を持つ¹。続いて \(T\setminus L\) の任意の二頂点が路連結だと示す。

\(u\) と \(v\) を \(T \setminus L\) の任意の頂点とする。このとき \(u\in V\setminus L\) かつ \(v\in V\setminus L\) だから、(b) より次の等式を得る:

\(T\) は連結より \(u\) から \(v\) への路は \(T\) に存在するので、\(T \setminus L\) における \(u\) から \(v\) への路も存在する。つまり \(T \setminus L\) で \(u\) と \(v\) は路連結である。

少なくとも一つの頂点を持つグラフ \(T\setminus L\) の任意の二頂点 \(u\), \(v\) が \(T\setminus L\) で路連結だと示せたので、\(T\setminus L\) は連結である。以上で補題 5.5.10 (a) は証明された。

(d): \(u\) と \(v\) を \(T \setminus L\) の任意の頂点とするとき、補題 5.5.10 (c) より二つの距離 \(d_{T}\left( u,v\right) \) と \(d_{T\setminus L}\left( u,v\right) \) は等しい。そこで、この距離を今後は \(d\left( u,v\right) \) と表記する (こうしても曖昧性は生じない)。

任意に \(v\in V\setminus L\) を取る。これから \(\operatorname*{ecc}\nolimits_{T}v=\operatorname*{ecc}\nolimits_{T\setminus L}v+1\) を示す。

\(u\) を \(d\left( v,u\right) \) が最大となる \(T \setminus L\) の頂点とする。このとき離心率の定義より \(\operatorname*{ecc}\nolimits_{T\setminus L}v=d\left( v,u\right) \) が成り立つ。一方で、\(T\setminus L\) の頂点である \(u\) は \(L\) に属さない。\(L\) は \(T\) の葉全体の集合だったから、\(u\) は \(T\) の葉でないと分かる。つまり \(u\) は \(T\) において \(2\) 以上の次数を持つ (少なくとも一つの頂点を持つ木の頂点の次数は \(0\) でないため)。

続いて、木 \(T\) における \(v\) から \(u\) への路 \(\mathbf{p}\) を考える。この路 \(\mathbf{p}\) の長さは \(d\left( v,u\right) \) である。\(u\) が \(2\) 以上の次数を持つので、\(u\) を含む \(T\) の辺が \(2\) 個以上存在する。よって \(u\) を含み \(\mathbf{p}\) の最後の辺でない \(T\) の辺 \(f\) を取れる²。この辺 \(f\) に注目する。\(f\) の \(u\) でない端点を \(w\) とする。\(\mathbf{p}\) の末尾に \(f\) と \(w\) 追加すると、\(v\) から \(w\) への歩道が得られる。\(f\) は \(\mathbf{p}\) の最後の辺ではないので、この歩道はバックトラックフリー歩道であり、従って (\(T\) は閉路を持たないので、命題 5.1.2 より) 路である。この路の長さは \(\mathbf{p}\) の長さに \(1\) を加えた \(d\left( v,u\right) +1\) であり、\(d\left( v,w\right) =d\left( v,u\right) +1\) が成り立つ。一方で離心率の定義からは次の等式が分かる:

一方、\(d\left( v,x\right) \) が最大となる \(T\) の頂点を \(x\) とする。このとき離心率の定義より \(\operatorname*{ecc}\nolimits_{T}v=d\left( v,x\right) \) が成り立つ。\(v\) から \(x\) への路の長さは \(1\) 以上³なので、この路には最後から二番目の頂点 \(y\) が存在する。このとき \(v\) から \(y\) への路は \(v\) から \(x\) への路から最後の辺と頂点を除去した路だから、\(d\left( v,y\right) =d\left( v,x\right) -1\) を得る。一方、容易に分かるように \(y\in V\setminus L\) が成り立つ⁴。言い換えれば、\(y\) は \(T \setminus L\) の頂点である。よって離心率の定義より次が分かる:

ここから \(\operatorname*{ecc}\nolimits_{T}v\leq\operatorname*{ecc}\nolimits_{T\setminus L}v+1\) を得る。これと式 \((2)\) より \(\operatorname*{ecc}\nolimits_{T}v=\operatorname*{ecc}\nolimits_{T\setminus L}v+1\) を得る。以上で補題 5.5.10 (d) は証明された。

(e): \(u\) と \(v\) を \(T \setminus L\) の任意の頂点とするとき、補題 5.5.10 (c) より二つの距離 \(d_{T}\left( u,v\right) \) と \(d_{T\setminus L}\left( u,v\right) \) は等しい。そこで、この距離を今後は \(d\left( u,v\right) \) と表記する (こうしても曖昧性は生じない)。

\(v \in L\) を \(T\) の葉とする。\(T\) における \(v\) の唯一の隣接頂点を \(w\) とする。\(\operatorname*{ecc}\nolimits_{T}v=\operatorname*{ecc}\nolimits_{T}w+1\) を示す必要がある。

まず、次の等式を証明する:

式 \((3)\) の証明: \(v\) は葉なので \(\deg v=1\) が成り立つ。言い換えれば、\(v\) を含む辺が \(T\) に唯一つ存在する。この辺を \(e\) とすれば、\(e\) の端点は \(v\) と \(w\) である (\(w\) は \(v\) の唯一の隣接頂点であるため)。木 \(T\) はループを持たないので \(v \neq w\) と \(d\left( v,w\right) =1\) を得る。

続いて \(u\in V\setminus\left\{ v\right\} \) を任意に取る。このとき \(T\) における \(v\) から \(u\) への路 \(\mathbf{w}\) は (\(u \neq v\) より) \(1\) 以上の長さを持つ。\(v\) を含む \(T\) の辺は \(e\) だけなので、\(\mathbf{w}\) の最初の辺は \(e\) である。よって \(\mathbf{w}\) から \(e\) を除去すると、\(w\) から \(u\) への路が得られる。つまり、\(v\) から \(u\) への路は \(w\) から \(u\) への路より長さが \(1\) だけ大きい。言い換えれば \(d\left( v,u\right) =d\left( w,u\right) +1\) であり、式 \((3)\) が証明された。

続いて、離心率の定義から次の等式が分かる:

\(d\left( v,v\right) =0\) と \(d\left( v,w\right) =1\) が成り立つので、上式右辺の最大値が達成されるのは \(u=v\) のときではない。よって最大値を考えるとき \(V\) から \(v\) を除去しても構わない。つまり上述の等式は次のように書き換えられる:

一方、離心率の定義からは次の等式も分かる:

これから、\(V\) から \(v\) を除去しても上式右辺の最大値が変化しないことを示す。言い換えれば、次の等式を示す:

式 \((6)\) の証明: 背理法で示す。式 \((6)\) が成り立たないと仮定する。このとき \(\left\{ d\left( w,u\right) \mid u\in V\right\} \) は \(u=v\) で最大値を取り、他の \(u\) の値では最大値を取らない。言い換えれば、次の不等式が成り立つ:

しかし、\(T\) は \(3\) 個以上の頂点を持つ木なので、\(v\) でも \(w\) でもない頂点 \(u\) を持つ。この \(u\) に注目する。\(u\in V\setminus\left\{ v\right\} \) なので、式 \((7)\) より \(d\left( w,v\right) >d\left( w,u\right) \) を得る。\(d\left( w,v\right) =d\left( v,w\right) =1\) だったから、\(1>d\left( w,u\right) \) が分かる。ここから \(d\left( w,u\right) = 0\) つまり \(w = u\) が分かる。しかし、これは \(w\) と \(u\) が異なる事実と矛盾する。よって仮定は偽であり、式 \((6)\) が証明された。

よって式 \((4)\) は次のように書き換えられる:

以上で補題 5.5.10 (e) は証明された。

(f): 補題 5.5.10 (e) より、任意の葉 \(v \in L\) はその唯一の隣接頂点 \(w\) より大きな離心率を持つ。よって離心率 \(\operatorname*{ecc}\nolimits_{T}v\) を最小化する \(T\) の頂点 \(v\) は \(L\) に属さない。言い換えれば、\(\operatorname*{ecc}\nolimits_{T}v\) を最小化する \(T\) の頂点 \(v\) は \(V\setminus L\) に属する。

一方、\(T\) の中心は「\(\operatorname*{ecc}\nolimits_{T}v\) を最小化する \(T\) の頂点」と定義される。前段落で示したように、そのような頂点は \(V \setminus L\) に属する。よって \(T\) の中心は「\(\operatorname*{ecc}\nolimits_{T}v\) を最小化する頂点 \(v\in V\setminus L\)」と特徴づけられる。また、補題 5.5.10 (d) より \(T\) の任意の頂点 \(v \in V \setminus L\) で \(\operatorname*{ecc}\nolimits_{T}v=\operatorname*{ecc}\nolimits_{T\setminus L}v+1\) が成り立つので、 \(T\) の頂点 \(v\in V\setminus L\) が \(\operatorname*{ecc}\nolimits_{T}v\) を最小化するのは、\(v\) が \(\operatorname*{ecc}\nolimits_{T\setminus L}v\) を最小化するとき、かつそのときに限る。よって \(T\) の中心は「\(\operatorname*{ecc}\nolimits_{T \setminus V}v\) を最小化する頂点 \(v\in V\setminus L\)」と特徴付けられる。これは \(T\setminus L\) の中心の定義そのもである。よって \(T\) の中心と \(T \setminus L\) の中心は一致する。以上で補題 5.5.10 (f) は証明された。□

[定理 5.5.9 の証明] (a) と (b) を \(\left\vert \operatorname*{V}\left( T\right) \right\vert \) に関する数学的帰納法で示す。

木 \(T\) を任意に取る。定理 5.5.9 の (a) と (b) が \(\left\vert \operatorname*{V}\left( T\right) \right\vert \) 個より少ない頂点を持つ任意の木で成り立つと仮定する。これから \(T\) に対しても二つの命題が成り立つことを示す。

\(\left\vert \operatorname*{V}\left( T\right) \right\vert \leq2\) なら二つの命題は明らかなので、一般性を失うことなく \(\left\vert \operatorname*{V}\left( T\right) \right\vert > 2\) と仮定する。つまり木 \(T\) は \(3\) 個以上の頂点を持つ。\(T\) に含まれる葉全体の集合を \(L\) とする。このとき定理 5.3.2 (a) より \(\left\vert L\right\vert \geq2\) が分かる。補題 5.5.10 と同様に多重グラフ \(T \setminus L\) を定義すると、補題 5.5.10 (f) より \(T\) の中心と \(T \setminus L\) の中心は一致する。

一方、補題 5.5.10 (a) からは \(T \setminus L\) が木であることが分かる。\(\left\vert L\right\vert \geq2 > 0\) なので、\(T \setminus L\) は \(T\) より少ない頂点を持つ。よって帰納法の仮定より、\(T \setminus L\) に対しては定理 5.5.9 の (a) と (b) が成り立つ。言い換えれば、木 \(T \setminus L\) の中心は \(1\) 個または \(2\) 個存在し、もし中心が \(2\) 個存在するなら、それらは隣接する。前段落で示したように \(T\) の中心と \(T \setminus L\) の中心は一致するので、前文は次のように書き換えられる: 木 \(T\) の中心は \(1\) 個または \(2\) 個存在し、もし中心が \(2\) 個存在するなら、それらは隣接する。つまり定理 5.5.9 の (a) と (b) は \(T\) に対しても成り立つ。以上で再帰ステップが完了したので、(a) と (b) の証明が完了した。

(c): 補題 5.5.10 (f) から従う。実際、\(T\) の頂点数が \(2\) 以下なら、\(T\) の全ての頂点が中心となる (容易に示せる)。\(T\) の頂点数が \(3\) 以上なら、補題 5.5.10 (f) よりアルゴリズムの「葉の除去」操作を適用しても \(T\) の中心はそのままだと分かる。つまり、元々の木 \(T\) の中心と葉を除去した後の木の中心は一致する。よって \(T\) の中心はアルゴリズムを最後まで実行したときに残る頂点と一致する。以上で定理 5.5.9 (c) は証明された。□

次の練習問題は木の中心に関するこれまでと異なるアプローチを示す:

グラフの中心に似た概念として重心がある。重心を簡単に議論する練習問題を示す:

練習問題 5.15

\(T\) を木とする。\(T\) の任意の頂点 \(v\) に対して、グラフ \(T\setminus v\) の最も大きな成分の大きさを \(c_{v}\) と表記する。 [\(T\setminus v\) は \(T\) から頂点 \(v\) と \(v\) を含む全ての辺を除去して得られるグラフを表す。また、成分は (本書では) 頂点の集合として定義されるので、その大きさとは含まれる頂点の個数を意味する。] \(c_{v}\) を最小化する \(T\) の頂点 \(v\) を \(T\) の重心 (centroid) と呼ぶ。

1. \(T\) の重心の個数は \(2\) 以下だと示せ。さらに、\(T\) が \(2\) 個の重心を持つとき、それらは隣接することを示せ。

2. 重心と中心が一致しない木 \(T\) を示せ。

[例: 各頂点に \(c_{v}\) の値を示すラベルを付けた木 \(T\) の例を示す:

\(5\) のラベルが付いた頂点が木 \(T\) の唯一の重心である。]

練習問題 5.15 (a) と定理 5.5.9 (a), (b) が似ている点に注目してほしい。