5.16. de Bruijn 列
5.16.1 定義
これまでに紹介したものより複雑な有向木の応用例を見よう。
最初にパズルを一つ: 次に示す周期的な列は、どんな特徴を持つだろうか?
この列が持つ素敵な特徴の一つとして、列の上で長さ \(4\) の「ウィンドウ」をスライドさせる (連続する \(4\) 要素を順に取る) と、長さ \(4\) のビット文字列として可能な \(16\) 個のビット文字列が全て得られることがある。加えて、ウィンドウが \(16\) 回スライドするまで同じビット文字列は得られない。長さ \(4\) のウィンドウを上に示した列の上でスライドさせる様子を次に示す:
ウィンドウに含まれるビット文字列の変化に注目すると、ウィンドウを一つ右に移動させるたびに先頭のビットが除去され、末尾にビットが新たに付け足されているのが分かる。つまり、長さ \(4\) のウィンドウを上に示した列に沿ってスライドさせて得られるビット文字列の列は、隣り合う二つのビット文字列が「前者の先頭のビットを除去して末尾に (\(0\) か \(1\) の) ビットを付け足すと後者になる」を満たし、それでいて長さ \(4\) のビット文字列として可能な \(16\) 個のビット文字列を全て含む。これは素敵な性質であり、グレイコードに似ていると言える (グレイコードは特定の長さの全ての文字列を \(1\) ビットずつ変化するように並べた列を利用する)。
ウィンドウの長さを \(4\) だけではなく任意の自然数とした場合でも同様の素敵な列を見つけられるだろうか?
例えば、ウィンドウの長さが \(3\) のときは次の列が条件を満たす:
もっと長いウィンドウではどうだろうか?
さらに、同じ質問を異なるアルファベットに対して考えることもできる。例えばビットの代わりに \(\left\{ 0,1,2\right\} \) をアルファベットとして使う (\(0\) と \(1\) からなる列ではなく \(0\), \(1\), \(2\) からなる列を考える) なら、長さ \(2\) のウィンドウに対して条件を満たすのは次の列である:
一般的なケースではどうなるだろうか? まずは用語を定義しよう:
\(n\), \(k\) を正整数、\(K\) を \(k\) 要素の集合とする。
\(K\) 上の \(n\) 次 de Bruijn 列 (de Bruijn sequence of order \(n\) on \(K\)) とは、\(K\) の要素から構成される \(k^{n}\) 要素の組 \(\left( c_{0},c_{1},\ldots,c_{k^{n}-1}\right) \) であって次の条件を満たすものを意味する:
-
\(K\) の要素からなる \(n\) 要素の組 \(\left( a_{1},a_{2},\ldots ,a_{n}\right) \in K^{n}\) のそれぞれに対して、次の等式が成り立つ \(r\in\left\{ 0,1,\ldots,k^{n}-1\right\} \) が唯一つ存在する:
\[ \left( a_{1},a_{2},\ldots,a_{n}\right) =\left( c_{r},c_{r+1},\ldots, c_{r+n-1}\right) \]
ここで \(c\) の添え字はモジュロ \(k^{n}\) で周期的に解釈する: つまり、任意の \(q\in\mathbb{Z}\) に対して \(c_{q+k^{n}}=c_{q}\) とする。例えば \(c_{k^{n}}=c_{0}\) や \(c_{k^{n}+1}=c_{1}\) が成り立つ。
例えば \(n=2\), \(\ k=3\), \(\ K=\left\{ 0,1,2\right\} \) とすれば、次に示す長さ \(9\) の列は \(K\) 上の \(n\) 次 de Bruijn 列である:
実際、この列を \(c_{0},c_{1},\ldots,c_{8}\) とすれば (そして \(c_{9}=c_{0}\) のように添え字を周期的に拡張すれば) 次が成り立つ:
この de Bruijn 列 \(\left( 0,0,1,1,2,2,0,2,1\right) \) は以前に示した周期的な列
に対応する。
5.16.2 de Bruijn 列の存在
de Bruijn 列は常に存在することが言える:
\(n\), \(k\) を正整数、\(K\) を \(k\) 要素集合とする。このとき \(K\) 上の \(n\) 次 de Bruijn 列は存在する。
有向グラフを使うアプローチが有望に思える。例えば、\(K^{n}\) に属する \(n\) 要素の組を頂点として、二頂点 \(i\), \(j\) が「\(i\) の先頭要素を除去し、末尾に \(K\) の要素を付け足すと \(j\) となる」を満たすとき、かつそのときに限って \(i\) から \(j\) への弧が存在する有向グラフを考えれば、このグラフのハミルトン閉路が \(K\) 上の \(n\) 次 de Bruijn 列と等しくなる。
しかし残念ながら、そういったグラフにおけるハミルトン閉路の存在を判定する条件は知られていない。そのため、このアプローチは袋小路に思える。
諦める前に、非直感的なアプローチを試してみよう: ハミルトン閉路と異なりオイラー回路なら存在の簡単な判定基準があるので、de Bruijn 列を (ハミルトン閉路ではなく) オイラー回路と解釈する!
このためには異なるグラフが必要になる。具体的には次の通りである: \(D\) を多重有向グラフ \(\left( K^{n-1},K^{n},\psi\right) \) とする。ここで写像 \(\psi\colon K^{n}\rightarrow K^{n-1}\times K^{n-1}\) は次の式で与えられる:
つまり、\(D\) の頂点は \(K\) の要素からなる (\(n\) 要素ではなく) \(n-1\) 要素の組であり、弧は \(K\) の要素からなる \(n\) 要素の組であり、弧 \(\left( a_{1},a_{2},\ldots,a_{n}\right) \) は始点 \(\left( a_{1},a_{2},\ldots,a_{n-1}\right) \) と終点 \(\left( a_{2},a_{3},\ldots,a_{n}\right) \) を持つ。言い換えれば、長さ \(n-1\) の列 \(i,j \in K^{n-1}\) が「\(i\) の先頭要素を除去し、末尾に \(K\) の要素を付け足すと \(j\) となる」を満たすとき、かつそのときに限って始点 \(i\) と終点 \(j\) を持つ弧が \(D\) に存在する。
\(D\) について次の事実が分かる:
-
多重有向グラフ \(D\) は強連結である。
証明: \(D\) 頂点を任意に二つ取って \(i\), \(j\) とするとき、\(i\) から \(j\) への歩道が存在すると示せばよい。しかし、これは容易に分かる: \(i\) の要素を先頭から一つずつ除去しながら \(j\) の要素を末尾に一つずつ追加していけば、\(i\) を \(j\) にできる。言い換えれば、組 \(k\) の第 \(p\) 要素を \(k_{p}\) と表す記法を使うとき、次の操作の列に対応する歩道が存在する:
\[ \begin{aligned} i & =\left( i_{1},i_{2},\ldots,i_{n-1}\right) \\ & \rightarrow\left( i_{2},i_{3},\ldots,i_{n-1},j_{1}\right) \\ & \rightarrow\left( i_{3},i_{4},\ldots,i_{n-1},j_{1},j_{2}\right) \\ & \rightarrow\cdots\\ & \rightarrow\left( i_{n-1},j_{1},j_{2},\ldots,j_{n-2}\right) \\ & \rightarrow\left( j_{1},j_{2},\ldots,j_{n-1}\right) =j \end{aligned} \]この歩道の長さが \(n-1\) であり、\(i\) から \(j\) への長さ \(n-1\) の歩道はこれ以外に存在しないことに注目してほしい。つまり、\(i\) から \(j\) への長さ \(n-1\) の歩道の個数は \(1\) である。この事実は後で利用される。
-
多重有向グラフ \(D\) は弱連結である (強連結な任意のグラフは弱連結なため)。
-
多重有向グラフ \(D\) は平衡である。さらに、\(D\) の任意の頂点は出次数 \(k\) と入次数 \(k\) を持つ。
証明: \(D\) の頂点を任意に取って \(i\) とする。\(i\) を始点に持つ弧は長さ \(n\) の列であり、最初の \(n-1\) 要素は \(i\) の全 \(n-1\) 要素に等しく、最後の第 \(n\) 要素は \(K\) の任意の要素である。つまり \(i\) を始点に持つ弧は \(\left\vert K\right\vert \) 個だけ存在する。言い換えれば、\(i\) の出次数は \(k\) である。同様の議論で \(i\) の入次数が \(k\) だとも示せる。つまり \(\deg^{-}i=\deg^{+}i\) が成り立つ。この等式が任意の頂点 \(i\) で成り立つから、\(D\) は平衡である。
-
多重有向グラフ \(D\) はオイラー回路を持つ。
証明: \(D\) が弱接続かつ平衡なので、Euler–Hierholzer の定理 (定理 4.7.2) から従う。あるいは、次のように BEST 定理 (定理 5.9.1) を使うこともできる: \(D\) の弧を任意に取って \(a\) として、\(a\) の始点を \(r\) とする。\(D\) は強連結より、\(r\) は \(D\) の始根である。よって定理 5.8.4 より、\(D\) は \(r\) を根とする全域有向木を持つ。つまり BEST 定理 (定理 5.9.1) の記法を使えば \(\tau\left( D,r\right) \neq 0\) が成り立つ。さらに、\(D\) の任意の頂点は \(k > 0\) の入次数を持つから、BEST 定理より次が分かる:
\[ \varepsilon\left( D,a\right) =\underbrace{\tau\left( D,r\right) }_{\neq 0}\cdot\underbrace{\prod_{u\in V}\left( \deg^{-}u-1\right) !}_{\neq0}\neq0 \]つまり、\(D\) は \(a\) を最後の弧に持つオイラー回路を持つ。
以上で \(D\) がオイラー回路 \(\mathbf{c}\) を持つことが分かった。このオイラー回路からは次のように de Bruijn 列が得られる:
\(\mathbf{c}\) の弧を順に \(p_{0},p_{1},\ldots,p_{k^{n}-1}\) とする。\(p\) の添え字をモジュロ \(k^{n}\) で周期的に拡張する (つまり任意の \(q\in\mathbb{N}\) に対して \(p_{q+k^{n}}=p_{q}\) と定義する) と、\(\mathbf{c}\) は閉路より \(p_{0},p_{1},p_{2},\ldots\) を弧とする無限歩道1を考えることができる。言い換えれば、任意の \(i\in\mathbb{N}\) に対して弧 \(p_{i}\) の終点が弧 \(p_{i+1}\) の始点に等しくなる。
さらに言い換えれば、任意の \(i \in \mathbb{N}\) に対して、\(p_{i}\) の最後の \(n-1\) 要素は \(p_{i+1}\) の最初の \(n-1\) 要素に等しい (\(p_{i}\) の終点は \(p_{i}\) の最後の \(n-1\) 要素であり、\(p_{i+1}\) の始点は \(p_{i+1}\) の最初の \(n-1\) 要素であるため)。よって、任意の \(i\in\mathbb{N}\) と \(j\in\left\{ 2,3,\ldots ,n\right\} \) に対して次の等式が成り立つ:
続いて、任意の \(i\in\mathbb{N}\) に対して長さ \(n\) の列 \(p_{i}\) の第 \(1\) 要素を \(x_{i}\) とする。このとき任意の \(q\in\mathbb{N}\) で \(x_{q+k^{n}}=x_{q}\) が成り立つ (\(p_{q+k^{n}}=p_{q}\) より)。言い換えれば、列 \(\left( x_{0},x_{1},x_{2},\ldots\right) \) は \(k^{n}\) 要素ごとに同じ値を取る。\(x_{i}\) の定義より、\(k^{n}\) 要素の組 \(\left( x_{0},x_{1},\ldots,x_{k^{n}-1}\right) \) は \(\mathbf{c}\) の弧 \(p_{0},p_{1},\ldots,p_{k^{n}-1}\) の第 \(1\) 要素からなる。
任意の \(i\in\mathbb{N}\) と \(s\in\left\{ 1,2,\ldots,n\right\} \) に対して、次が成り立つ:
つまり、任意の \(i \in \mathbb{N}\) に対して \(p_{i}\) の要素は第 \(1\) 要素から順に \(x_{i},x_{i+1},\ldots,x_{i+n-1}\) である。言い換えれば、次の等式が成り立つ:
ところで、\(\mathbf{c}\) はオイラー回路だった。よって \(D\) の任意の弧は \(p_{0},p_{1},\ldots,p_{k^{n}-1}\) にちょうど一度だけ含まれる。言い換えれば、\(K\) の要素からなる長さ \(n\) の列 (\(K^{n}\) の要素) はそれぞれ \(p_{0},p_{1},\ldots,p_{k^{n}-1}\) にちょうど一度だけ含まれる (\(D\) の弧は \(K\) の要素からなる長さ \(n\) の列であるため)。つまり、\(i\) を \(0\) から \(k^{n}-1\) まで増加させるとき、長さ \(n\) の列 \(p_{i}\) は \(K^{n}\) に属する値をそれぞれ一度ずつ取る。
式 \((4)\) を使うと、この事実を次のように書き換えることができる: \(i\) を \(0\) から \(k^{n}-1\) まで増加させるとき、\(n\) 要素の組 \(\left( x_{i},x_{i+1},\ldots,x_{i+n-1}\right) \) は \(K^{n}\) に属する値をそれぞれ一度ずつ取る。言い換えれば、任意の \(\left( a_{1},a_{2},\ldots,a_{n}\right) \in K^{n}\) に対して、\(\left( a_{1},a_{2},\ldots,a_{n}\right) =\left( x_{r},x_{r+1},\ldots,x_{r+n-1}\right) \) を満たす \(r\in\left\{ 0,1,\ldots,k^{n}-1\right\} \) が唯一つ存在する。
よって長さ \(k^{n}\) の列 \(\left( x_{0},x_{1},\ldots,x_{k^{n}-1}\right) \) は \(K\) 上の \(n\) 次 de Bruijn 列である。以上で de Bruijn 列の存在が示せたので、定理 5.16.2 は証明された。□
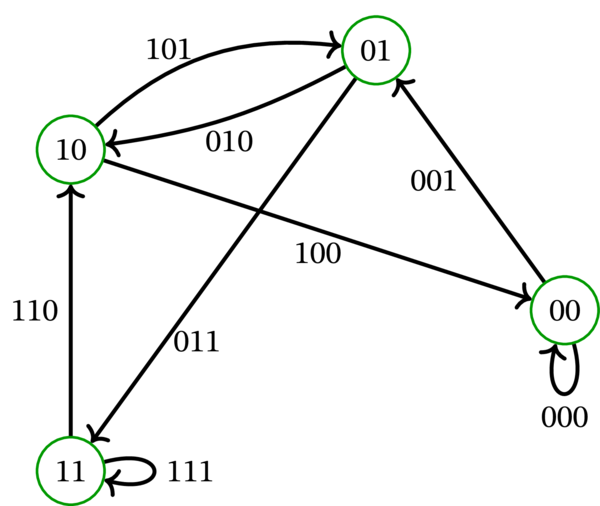
例 5.16.3 と同様に \(n=3\), \(\ k=2\), \(\ K=\left\{ 0,1\right\}\) とする。\(D\) のオイラー回路 \(\mathbf{c}\) として次の列を取ったとする:
このオイラー回路の弧の第 \(1\) 要素を並べると \(0010111\) となり、これは確かに \(\left\{ 0,1\right\} \) 上の \(3\) 次 de Bruijn 列となる。この列 (を周期的に拡張した無限列 \(||:0010111:||\)) において、任意の連続する \(3\) 要素には対応する \(\mathbf{c}\) の弧が存在する。
定理 5.16.2 は de Bruijn 列に関する理論の出発地点でしかない。様々な特徴を持つ特別な de Bruijn 列がいくつか知られている。そういった de Bruijn 列に関するサーベイとして [Freder82] がある23 (このサーベイは de Bruijn 列を「full length nonlinear shift register sequences」と呼んでいる)。
de Bruijn 列に似た定義を持つ列もいくつかある。その一部は [ChDiGr92] で解説されている (この論文で紹介されている問題の中には現在でも未解決のものが存在する)。最近になって非常に有名になったものに「universal cycle for permutations」がある ── 全ての置換 (\(K\) の異なる要素からなる長さ \(n\) の列) を含む列を意味する。この文字列の長さを最小化する問題に関する近年の進展 (4chan という悪名高いサイトに投稿された文章によるものを含む) は [EngVat18] から確認できる。この問題が考える文字列ではある程度の重複が避けられないので、オイラー回路は役に立たない。
5.16.3 de Bruijn 列の数え上げ
定理 5.16.2 で de Bruijn 列の存在が証明できたので、次は de Bruijn 列の個数を数えてみよう!
質問: \(n\), \(k\) を正整数、\(K\) を \(k\) 要素の集合とする。\(K\) 上の \(n\) 次 de Bruijn 列はいくつあるか?
この質問に答えるには、上で構築した有向グラフ \(D\) に BEST 定理 (定理 5.9.1) を適用すればよさそうに思える。しかし、\(D\) は何らかの無向グラフ \(G\) を使って \(G^{\operatorname*{bidir}}\) と書けるわけではないので、無向グラフに対する行列木定理 (定理 5.15.1) は適用できない。しかし、\(D\) は平衡な多重有向グラフであり、そういった有向グラフに対しては無向グラフに対する行列木定理に似た命題が成り立つ:
\(D=\left( V,A,\psi \right) \) を平衡な多重有向グラフとする。ある \(n \in \mathbb{N}\) で \(V=\left\{ 1,2,\ldots,n\right\} \) だと仮定する。
\(D\) のラプラシアンを \(L\) とする。このとき:
-
\(D\) の頂点を任意に取って \(r\) とする。このとき次の等式が成り立つ:
\[ \left(\text{\# } r \text{ を終根とする } D \text{ の全域有向木} \right) = \det\left( L_{\sim r,\sim r}\right) \]さらに、この数値は \(r\) に依存しない。
-
\(t\) を不定元とする。行列式 \(\det\left( tI_{n}+L\right) \) を \(t\) の多項式として展開したときの \(t\) の係数を \(c_{0},c_{1},\ldots,c_{n}\) とする (ここで \(I_{n}\) は \(n\times n\) の恒等行列を表す)。言い換えれば、次の等式が成り立つように \(c_{0},c_{1},\ldots,c_{n}\) を定める:
\[ \det\left( tI_{n}+L\right) =c_{n}t^{n}+c_{n-1}t^{n-1}+\cdots+c_{1}t^{1}+c_{0}t^{0} \]このとき、次の等式が成り立つ:
\[ \left(\text{\# } r \text{ を終根とする } D \text{ の全域有向木} \right) =\dfrac{1}{n}c_{1} \] -
\(L\) の固有値を \(\lambda_{1},\lambda_{2},\ldots,\lambda_{n}\) とする。ただし \(\lambda_{n} = 0\) とする。このとき、\(D\) の任意の頂点 \(r\) に対して次の等式が成り立つ:
\[ \left(\text{\# } r \text{ を終根とする } D \text{ の全域有向木} \right) =\dfrac{1}{n}\cdot\lambda_{1}\lambda_{2}\cdots\lambda_{n-1} \] -
\(L\) の固有値を \(\lambda_{1},\lambda_{2},\ldots,\lambda_{n}\) とする。ただし \(\lambda_{n}=0\) とする。\(D\) の全ての頂点が \(1\) 以上の出次数を持つなら、次の等式が成り立つ:
\[ \left(\text{\# } D \text{ のオイラー回路} \right) =\left\vert A\right\vert \cdot\dfrac{1}{n}\cdot\lambda_{1}\lambda_{2}\cdots\lambda_{n-1}\cdot \prod_{u\in V}\left( \deg^{+}u-1\right) ! \]
(a): 等式は行列木定理 (定理 5.14.7) から分かる。後は \(r\) を終根とする \(D\) の全域有向木の個数が \(r\) に依存しないと示せばよいが、これは系 5.12.1 である。
(b): 定理 5.15.1 (b) (無向グラフに対する同様の命題) と同様に (a) から従う4。
(c): 定理 5.15.1 (c) (無向グラフに対する同様の命題) と同様に (b) から従う。
(d): \(D\) の全ての頂点が \(1\) 以上の出次数を持つと仮定する。このとき次の等式が成り立つ:
一方、\(a\) を \(D\) の任意の弧、\(r\) を \(a\) の始点とするとき、BEST' 定理 (定理 5.10.4) と (c) より次の等式が成り立つ:
よって次を得る:
以上で (d) は証明された。□
では、最初の質問に答えよう ── これから \(K\) 上の \(n\) 次 de Bruijn 列の個数を求める。
定理 5.16.2 の証明で定義した有向グラフ \(D\) を考える。\(D\) のオイラー回路が見つかれば、そこから \(K\) 上の \(n\) 次 de Bruijn 列を構築できる。実は、この操作は逆方向にも行える。つまり、次の写像は全単射である:
よって bijection principle から次の等式を得る:
一方で定理 5.6.15 (d) からは次の等式が分かる:
ここで \(\lambda_{1},\lambda_{2},\ldots,\lambda_{k^{n-1}}\) は \(D\) のラプラシアンの固有値を表す (ただし \(\lambda_{k^{n-1}}=0\) とする)。
先ほど示したように、\(D\) の各頂点の出次数は \(k\) である。つまり任意の \(u\in K^{n-1}\) に対して \(\deg ^{+}u=k\) が成り立つ。よって次の等式が分かる:
また、次の等式も成り立つ:
後は \(\lambda_{1}\lambda_{2}\cdots\lambda_{k^{n-1}-1}\) を計算すればよい。\(L\) の固有値はどうすれば計算できるだろうか?
今考えている有向グラフ \(D\) のラプラシアン \(L\) は \(k^{n-1}\times k^{n-1}\) 行列であり、その行と列は \(K^{n-1}\) に属する長さ \(n-1\) の列で特定される。数学的に厳密になるなら、ここで \(D\) の頂点を \(1,2,\ldots ,k^{n-1}\) に変更し、行と列に well-defined な順序が付いた「数学的に正しい」行列を考える必要がある。ただ、本書ではそうせず、名前の変更を読者に任せる。あるいは、行と列の特定に自然数以外のものを利用できる、より一般的な行列の概念を使うと考えてもよい (詳細は https://mathoverflow.net/questions/317105 を見てほしい)。
有向グラフ \(D\) の隣接行列を \(C\) とする。\(C\) は \(k^{n-1}\times k^{n-1}\) 行列 (行と列は \(K^{n-1}\) に属する長さ \(n-1\) 要素の列で特定される) であり、その \(\left( i,j\right) \) 要素は始点 \(i\) と終点 \(j\) を持つ \(D\) の弧の個数に等しい。特に、\(C\) のトレースは \(D\) のループの個数に等しい。容易に分かるように、\(D\) のループは任意の \(x \in K\) を使って \(\left( x,x,\ldots,x\right) \in K^{n}\) と書けるから、\(D\) は \(k\) 個のループを持つ。よって \(C\) のトレースは \(k\) と分かる。
ラプラシアンの定義を思い出せば、ラプラシアンと隣接行列には次の関係がある:
ここで \(\Delta\) は対角行列であり、その対角成分は対応する \(D\) の頂点の出次数に等しい。\(D\) の任意の頂点は出次数が \(k\) だから、\(\Delta\) は \(k^{n-1}\times k^{n-1}\) 恒等行列 \(I\) を使って \(k \cdot I\) と書ける。よって上式は次のように変形できる:
よって \(C\) の固有値を \(\gamma_{1},\ \gamma_{2},\ldots,\ \gamma_{k^{n-1}}\) とすれば、\(k-\gamma_{1},\ k-\gamma_{2},\ldots,\ k-\gamma_{k^{n-1}}\) が \(L\) の固有値となる。後は \(\gamma_{1},\ \gamma_{2},\ldots,\ \gamma_{k^{n-1}}\) を求めればよい。
ここで、全要素が \(1\) に等しい \(k^{n-1}\times k^{n-1}\) 行列を \(J\) とする (\(J\) の行と列も \(K^{n-1}\) に属する長さ \(n-1\) 要素の列で特定される)。\(J\) の固有値が
であることは簡単に示せる。
続いて、非常に天下り的となるが、次の等式を証明する:
証明: 行列 \(C^{n-1}\) の任意の要素が \(1\) だと示せばよい。つまり \(D\) の頂点を任意に二つ取って \(i\), \(j\) として、\(C^{n-1}\) の \(\left( i,j\right) \) 要素が \(1\) だと示せばよい。
定理 4.5.10 で触れた隣接行列の冪の組合せ論的な解釈を思い出してほしい: 任意の \(\ell\in\mathbb{N}\) に対して、\(C^{\ell}\) の \(\left( i,j\right) \) 要素は (\(D\) における) \(i\) から \(j\) への長さ \(\ell\) の歩道の個数に等しい。よって特に、\(C^{n-1}\) の \(\left( i,j\right) \) 要素は (\(D\) における) \(i\) から \(j\) への長さ \(n-1\) の歩道の個数に等しい。定理 5.16.2 の証明で見たように、この個数は \(1\) である。よって \(C^{n-1}=J\) が分かる。
この事実が \(C\) の固有値の計算にどう役立つのだろうか? \(C\) の固有値を \(\gamma _{1},\ \gamma_{2},\ldots,\ \gamma_{k^{n-1}}\) とする。このとき任意の \(\ell\in\mathbb{N}\) に対して、\(C^{\ell}\) の固有値は \(\gamma_{1}^{\ell },\ \gamma_{2}^{\ell},\ldots,\ \gamma_{k^{n-1}}^{\ell}\) である (この事実は任意の正方行列で成り立つ。Jordan 標準形か行列の三角化を使って示すのが最も簡単だろう)。よって特に、\(C^{n-1}=J\) の固有値は \(\gamma_{1}^{n-1},\ \gamma_{2}^{n-1},\ldots,\ \gamma_{k^{n-1}}^{n-1}\) である。一方で \(J\) の固有値は
だと先ほど示した。よって \(\gamma_{1}^{n-1},\ \gamma_{2}^{n-1},\ldots,\ \gamma_{k^{n-1}}^{n-1}\) は一つを除いて全て \(0\) に等しい (\(0\) でない唯一の値はここでは特定できない: \(k^{n-1}\) の \(n-1\) 乗根は \(\mathbb{C}\) を考えに入れるとき一意に定まらない)。言い換えれば、\(C\) は \(0\) でない固有値を一つだけ持つ。正方行列の固有値の和はトレースに等しいことが知られているので、\(C\) の \(0\) でない唯一の固有値は \(C\) のトレースに等しい。\(C\) のトレースは \(k\) だから、\(C\) の \(0\) でない唯一の固有値は \(k\) だと分かる。
以上で \(C\) の固有値が
だと分かった。よって \(L\) の固有値は
だと分かる (\(C\) の固有値が \(\gamma_{1},\ \gamma_{2},\ldots,\ \gamma_{k^{n-1}}\) のとき \(L\) の固有値は \(k-\gamma_{1},\ k-\gamma_{2},\ldots,\ k-\gamma_{k^{n-1}}\) であるため)。言い換えれば、\(L\) の固有値は
である。つまり式 \((6)\) における \(\lambda_{1},\lambda_{2},\ldots,\lambda_{k^{n-1}-1}\) は全て \(k\) に等しい。よって式 \((6)\) は次のように変形できる:
よって式 \((5)\) から次の等式を得る:
以上で次の定理が証明された:
\(n\), \(k\) を正整数、\(K\) を \(k\) 要素集合とする。このとき次の等式が成り立つ:
非常に綺麗な (そして非常に巨大な) 解答が得られた!
ここに示した証明は [Stanle18, Chapter 10] を参考にしている。定理 5.16.6 の組合せ論的な (線形代数を一切使わない) 証明は [BidKis02] から確認できる。
-
無限歩道の形式的な定義は与えていないものの、容易に想像できるだろう。 ↩︎
-
そういった de Bruijn 列の一部 (例えば「prefer-one」や「prefer-opposite」) はオイラー回路を見つけるアルゴリズムの異なる実装と等価である。本書で示した BEST 定理の証明でも特定の条件を満たすオイラー回路を構築するステップがあった。 ↩︎
-
著者の気に入っている de Bruijn 列は「長さが \(n\) の約数である Lyndon 文字列を辞書式昇順に並べた列」である (\(K\) の要素に対して定義された全順序が仮定される)。この列の構築について詳しくは [Moreno04] を見てほしい。 ↩︎
-
詳しい議論を示す: 無向グラフに対する行列木定理 (定理 5.15.1) の証明と同じ議論で \(c_{1}=\sum_{r=1}^{n}\det\left( L_{\sim r,\sim r}\right) \) が分かる。一方、(a) より \(\det\left( L_{\sim r,\sim r}\right) \) は \(r\) に依存しないので、\(\sum _{r=1}^{n}\det\left( L_{\sim r,\sim r}\right) \) は \(n\) 個の同じ値の和だと分かる。よって、この和は \(D\) の任意の頂点 \(r\) を使って \(n\cdot \det\left( L_{\sim r,\sim r}\right) \) と書ける。この事実を使えば、\(D\) の任意の頂点 \(r\) を使って等式 \(c_{1}=\sum_{r=1}^{n}\det\left( L_{\sim r,\sim r}\right) \) を \(c_{1}=n\cdot\det\left( L_{\sim r,\sim r}\right) \) と書き換えられる。つまり、任意の \(D\) の任意の頂点 \(r\) に対して \(\det\left( L_{\sim r,\sim r}\right) =\dfrac{1}{n}c_{1}\) が成り立つ。(a) からは
\[ \left(\text{\# } r \text{ を終根とする } D \text{ の全域有向木}\right) =\det\left( L_{\sim r,\sim r}\right) \]が分かるので、\(\det\left( L_{\sim r,\sim r}\right) =\dfrac{1}{n}c_{1}\) を代入すれば
\[ \left(\text{\# } r \text{ を終根とする } D \text{ の全域有向木}\right) =\dfrac{1}{n}c_{1} \]を得る。 ↩︎
-
詳細な議論を示す: 行列 \(J\) は全ての行が同じなので、\(J\) の階数は \(1\) と分かる。つまり \(J\) は \(0\) でない固有値を一つだけ持つ。この \(0\) でない唯一の固有値が \(k^{n-1}\) だと示せばよい。正方行列の固有値の和はトレースに等しいことが知られているので、\(0\) でない固有値が一つだけなら、それはトレースに等しい。この事実を \(J\) に適用すれば、\(J\) の \(0\) でない唯一の固有値は \(k^{n-1}\) だと分かる。 ↩︎