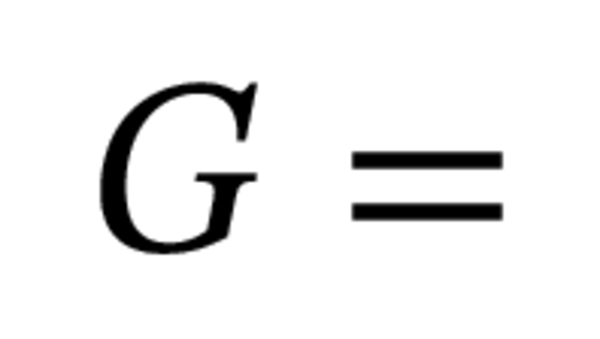5.2. 森と木の定義と性質

目次

5.2.1定義

それでは、本章の主人公二人を紹介しよう:

定義 5.2.1

閉路を持たない多重グラフを森 (forest) と呼ぶ。 [特に、森は二つの異なる平行な辺を持たない。さらにループも持たない。]

定義 5.2.2

連結な森を木 (tree) と呼ぶ。

例 5.2.3

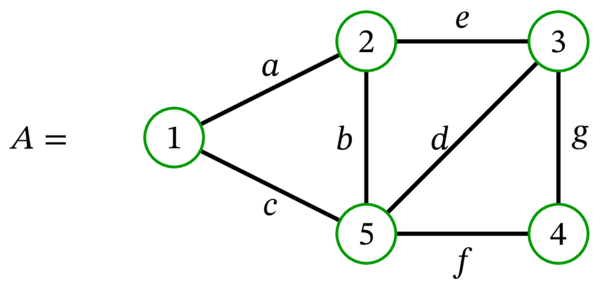
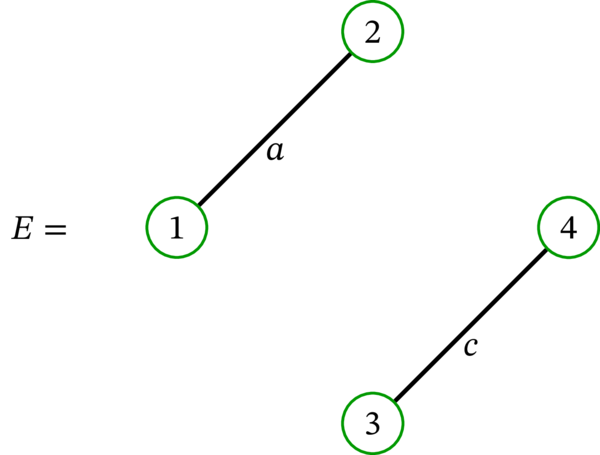
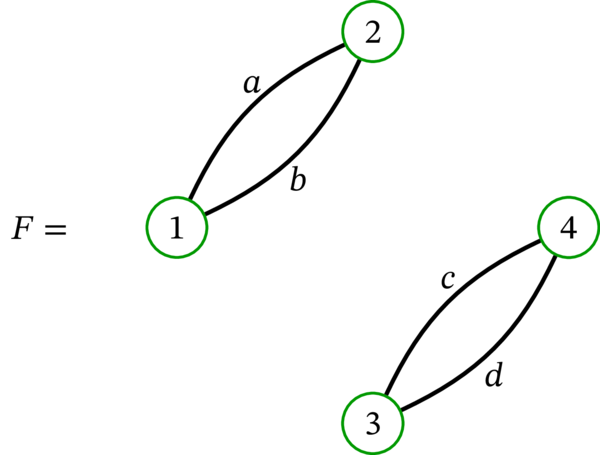
次の多重グラフを考える:

[\(G\) は頂点を持たないグラフである。] どのグラフが森で、どのグラフが木だろうか？

  • グラフ \(A\) は閉路を (いくつか) 持つので森ではない。従って \(A\) は木でもない。

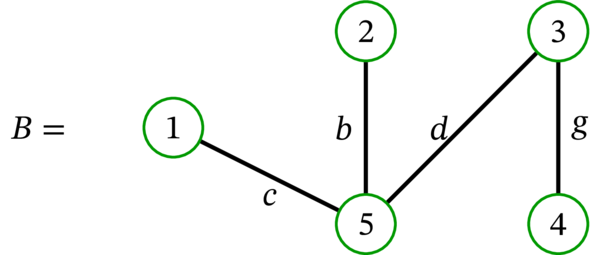
  • グラフ \(B\) は木である。

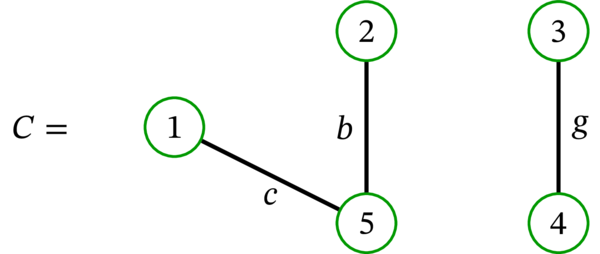
  • グラフ \(C\) は森ではあるものの、連結でないので木ではない。

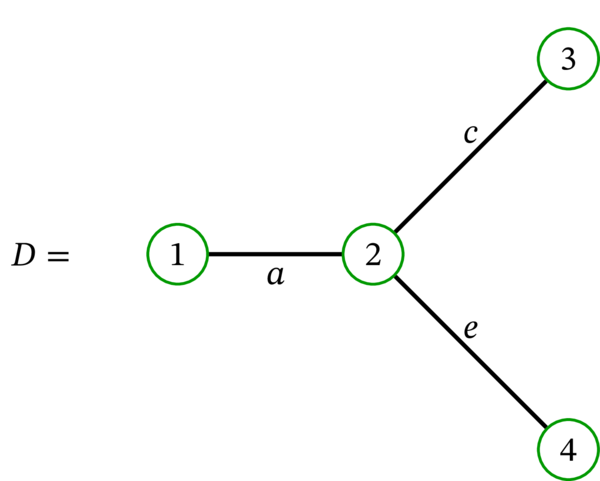
  • グラフ \(D\) は木である。

  • グラフ \(E\) は森ではあるものの、木ではない。

  • グラフ \(F\) は閉路を持つので森ではない。

  • グラフ \(G\) (頂点と辺の個数がいずれも \(0\) のグラフ) は森ではあるものの、連結でないので木ではない。 [思い出そう: グラフが連結とは、成分の個数が \(1\) であることを言う。\(G\) の成分の個数は \(0\) である。]

  • グラフ \(H\) は木である。

5.2.2木の同値性定理

木は様々な性質で特徴付けられる:

定理 5.2.4

[木の同値性定理 (the tree equivalence theorem)] \(G=\left( V,E,\varphi\right) \) を多重グラフとする。このとき、次の八個の命題は同値である:

  • 命題 T1: 多重グラフ \(G\) は木である。

  • 命題 T2: 多重グラフ \(G\) がループを持たず、\(V\neq\varnothing\) が成り立ち、任意の \(u \in V\) と \(v \in V\) に対して \(u\) から \(v\) への路が唯一つ存在する。

  • 命題 T3: \(V\neq\varnothing\) が成り立ち、任意の \(u \in V\) と \(v \in V\) に対して \(u\) から \(v\) へのバックトラックフリー歩道が唯一つ存在する。

  • 命題 T4: 多重グラフ \(G\) が連結であり、\(\left\vert E\right\vert =\left\vert V\right\vert -1\) が成り立つ。

  • 命題 T5: 多重グラフ \(G\) が連結であり、\(\left\vert E\right\vert < \left\vert V\right\vert \) が成り立つ。

  • 命題 T6: \(V\neq\varnothing\) が成り立ち、\(G\) が森であり、\(G\) に任意の辺を加えると閉路が生じる。

  • 命題 T7: 多重グラフ \(G\) が連結であり、\(G\) から任意の辺を除去すると連結でなくなる。

  • 命題 T8: 多重グラフ \(G\) が森であり、\(\left\vert E\right\vert \geq\left\vert V\right\vert -1\) と \(V\neq \varnothing\) が成り立つ。

[証明] 次の図のように証明を進める:

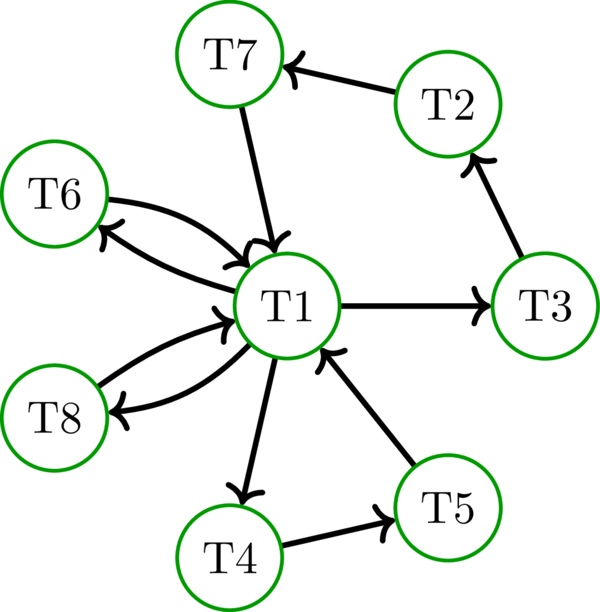
この有向グラフの \(\text{T}i\) から \(\text{T}j\) への弧は \(\text{T}i \Longrightarrow \text{T}j\) という命題を表す。この有向グラフは強連結 (任意の \(\text{T}i\) から任意の \(\text{T}j\) に弧をたどって到達可能) なので、その弧に対応する命題を全て証明すれば定理 5.2.4 が証明できる。

T1 \(\Longrightarrow\) T3 の証明: 命題 T1 が成り立つと仮定する。このとき \(G\) は木なので、\(G\) は連結であって \(V \neq \varnothing\) が成り立つ。任意の \(u \in V\) と \(v \in V\) に対して、\(u\) から \(v\) へのバックトラックフリー歩道が唯一つ存在することを示せばよい。\(G\) は連結なので、そのような歩道は存在する。後は唯一性を示す必要がある。ただ、これも易しい: ある \(u \in V\) と \(v\in V\) に対して \(u\) から \(v\) へのバックトラックフリー歩道が二つ存在するなら、定理 5.1.3 より \(G\) は閉路を持つ。このとき \(G\) は森ではなく、木でもない。よって \(u\) から \(v\) へのバックトラックフリー歩道は一つしか存在しない。これで命題 T3 が示せたので、T1 \(\Longrightarrow\) T3 は証明された。

T3 \(\Longrightarrow\) T2 の証明: 命題 T3 が成り立つと仮定する。T2 が成り立つと示せばよい。まず、\(G\) はループを持たない。なぜなら、仮にループ \(e\) が存在するなら、\(e\) の端点を \(u\) としたとき \(\left( u\right) \) と \(\left( u,e,u\right) \) が \(u\) から \(u\) への二つの異なるバックトラックフリー歩道となって T3 と矛盾するからである。後は任意の \(u \in V\) と \(v \in V\) に対して \(u\) から \(v\) への路が唯一つ存在すると示す必要がある。系 3.3.10 より、\(u\) から \(v\) への歩道の存在は \(u\) から \(v\) への路の存在を意味する。さらに、\(u\) から \(v\) へのバックトラックフリー歩道の唯一性が \(u\) から \(v\) への路の唯一性を意味する (任意の路はバックトラックフリー歩道であるため)。これで T3 \(\Longrightarrow\) T2 は証明された。

T2 \(\Longrightarrow\) T7 の証明: 命題 T2 が成り立つと仮定する。このとき \(G\) は連結である。\(G\) から任意の辺 \(e\) を除去したとする。\(e\) の端点を \(u\), \(v\) とすると、\(G\) はループを持たないので \(u \neq v\) が成り立つ。グラフ \(G\setminus e\) に \(u\) から \(v\) への路は存在できない: もし存在するなら、その路と \(\left( u,e,v\right) \) が \(G\) における \(u\) から \(v\) への二つの異なる路となって命題 T2 と矛盾する。よって \(G \setminus e\) は連結でない。まとめると \(G\) は連結であり、\(G\) から任意の辺を除去すると連結でなくなる。つまり命題 T7 が成り立つ。

T7 \(\Longrightarrow\) T1 の証明: 命題 T7 が成り立つと仮定する。\(G\) が木だと示せばよい。仮定より \(G\) は連結なので、\(G\) が森である、つまり \(G\) が閉路を持たないことを示す必要がある。仮に \(G\) が閉路を持つなら、その閉路に含まれる辺 \(e\) を除去したグラフ \(G\setminus e\) は連結なままとなる (系 5.1.5 (a) より \(\operatorname*{conn}\left( G\setminus e\right) =\operatorname*{conn}G=1\) が分かる)。これは T7 と矛盾するので、\(G\) は閉路を持たず、森である。これで T1 は証明された。

T1 \(\Longrightarrow\) T6 の証明: 命題 T1 が成り立つと仮定する。このとき \(G\) は木である。\(G\) に新しく任意の辺を加えると閉路が生じることを示せばよい (命題 T6 の他の部分は明らかである)。

\(G\) に新しい辺 \(f\) を加えたとして、\(f\) の端点を \(u\), \(v\) とする。グラフ \(G\) は連結なので、\(f\) を使わない \(u\) から \(v\) への路が存在する。この路に \(f\) を加えると閉路が得られる。よって \(G\) に任意の新しい辺 \(f\) を加えたグラフは閉路を持つ。これで命題 T6 は証明された。

T6 \(\Longrightarrow\) T1 の証明: 命題 T6 が成り立つと仮定する。このとき \(G\) は森だから、後は \(G\) が連結だと示せばよい。

背理法で示す。\(G\) の二頂点 \(u\), \(v\) が \(G\) で路連結でないと仮定する。このとき、\(u\) と \(v\) を端点とする新しい辺 \(f\) をグラフ \(G\) に追加しても新しい閉路が生じない (もし生じるなら、\(G\) は森より閉路を持たないのでその閉路は \(f\) を含む。その閉路から \(f\) を除去すると \(u\) から \(v\) への路が得られるので仮定と矛盾する)。これは命題 T6 と矛盾する。

よって \(G\) は連結な森すなわち木である。これで命題 T1 は証明された。

T1 \(\Longrightarrow\) T8 の証明: 命題 T1 が成り立つと仮定する。このとき \(G\) は木であり、明らかに森でもある。後は \(\left\vert E\right\vert \geq\left\vert V\right\vert -1\) を示せばよい。

定理 5.1.9 (a) より \(\operatorname*{conn}G\geq\left\vert V\right\vert -\left\vert E\right\vert \) が分かる。一方で \(G\) は連結より \(\operatorname*{conn}G=1\) なので、\(1=\operatorname*{conn}G\geq\left\vert V\right\vert -\left\vert E\right\vert \) を得る。これを変形すれば \(\left\vert E\right\vert \geq\left\vert V\right\vert -1\) であり、命題 T8 は証明された。

T8 \(\Longrightarrow\) T1 の証明: 命題 T8 が成り立つと仮定する。このとき \(G\) は森なので、後は \(G\) が連結だと示せばよい。\(G\) は森より閉路を持たないので、定理 5.1.9 (b) より \(\operatorname*{conn}G=\left\vert V\right\vert -\left\vert E\right\vert \leq1\) が分かる (命題 T8 より \(\left\vert E\right\vert \geq\left\vert V\right\vert -1\) が成り立つため)。一方で \(V\neq\varnothing\) より \(\operatorname*{conn}G\geq1\) なので、二つの結果を合わせると \(\operatorname*{conn}G=1\) を得る。つまり \(G\) は連結な森すなわち木であり、命題 T1 は成り立つ。

T1 \(\Longrightarrow\) T4 の証明: 命題 T1 が成り立つと仮定する。このとき \(G\) は木、すなわち連結な森である。森の定義より \(G\) は閉路を持たないので、定理 5.1.9 (b) から \(\operatorname*{conn}G=\left\vert V\right\vert -\left\vert E\right\vert \) を得る。さらに \(G\) は連結なので、\(\left\vert V\right\vert -\left\vert E\right\vert =\operatorname*{conn}G=1\) が成り立つ。つまり \(\left\vert E\right\vert =\left\vert V\right\vert -1\) であり、命題 T4 は成り立つ。

T4 \(\Longrightarrow\) T5 の証明: 明らかである。

T5 \(\Longrightarrow\) T1 の証明: 命題 T5 が成り立つと仮定する。このときグラフ \(G\) は連結であり、\(\left\vert E\right\vert < \left\vert V\right\vert \) が成り立つ。よって \(\left\vert E\right\vert \leq\left\vert V\right\vert -1\) であり、ここから \(1\leq\left\vert V\right\vert -\left\vert E\right\vert \) を得る。これと \(G\) が連結である事実から \(\operatorname*{conn}G=1\leq\left\vert V\right\vert -\left\vert E\right\vert \) が分かる。一方で定理 5.1.9 (a) からは \(\operatorname*{conn}G\geq\left\vert V\right\vert -\left\vert E\right\vert \) だと分かるので、二つの不等式を組み合わせると \(\operatorname*{conn}G=\left\vert V\right\vert -\left\vert E\right\vert \) を得る。よって定理 5.1.9 (b) より \(G\) は閉路を持たない。つまり \(G\) は森であり、\(G\) は連結より木でもある。これで T1 は証明された。

先述したように、これまでに示してきた命題があれば命題 T1, T2, ..., T8 が同値だと示せる。以上で定理 5.2.4 は証明された。□

木と森の間にある次の関係も分かる:

命題 5.2.5

\(G\) を多重グラフ、\(C_{1},C_{2},\ldots,C_{k}\) を \(G\) の成分とする。このとき、\(G\) が森となるのは誘導部分グラフ \(G\left[ C_{1}\right] ,G\left[ C_{2}\right] ,\ldots,G\left[ C_{k}\right] \) が全て木であるとき、かつそのときに限る。

[証明] \(\Longrightarrow\): \(G\) が森だと仮定する。このとき森の定義より \(G\) は閉路を持たない。よって誘導部分グラフ \(G\left[ C_{1}\right] ,G\left[ C_{2}\right] ,\ldots,G\left[ C_{k}\right] \) も閉路を持たない (もし閉路を持つなら、その閉路は \(G\) の閉路にもなる)。言い換えれば、これらの誘導部分グラフは全て森である。加えて連結でもある (成分に関する誘導部分グラフは常に連結となる) ので、連結な森すなわち木と分かる。

\(\Longleftarrow\): 誘導部分グラフ \(G\left[ C_{1}\right] ,G\left[ C_{2}\right] ,\ldots,G\left[ C_{k}\right] \) が全て木だと仮定する。木は閉路を持たないので、\(G\) も閉路を持たない (もし \(G\) が閉路を持つなら、それは誘導部分グラフのいずれかで閉路となる1)。言い換えれば、\(G\) は森である。□

5.2.3まとめ

木の性質を簡単にまとめておく:

\(T=\left( V,E,\varphi\right) \) を木とする。このとき...

Remark 5.2.6

コンピューター科学者が使う「木」の概念は本書で定義したものに似ているものの、全く同じではない。具体的に言うと、彼らが考える木は「根 (root)」を持ち、頂点間に親子関係が存在することがよくある (一つの頂点が根となり、各辺において根に近い端点がもう一方の「親」となる)。さらに多くの場合、各頂点が持つ子には全順序が定義される。こういった追加データを持つ木は各頂点が「根の \(4\) 番目の子の \(3\) 番目の子」のような路表現 (path description, 根からの自身への路) を持つので、オブジェクトの管理に利用できる。ただ、こういった特別な木は残念ながら本書の範囲から大きく離れる。これからはグラフとしての木を考え、必要なときに限って構造を持った木を考える。

練習問題 5.1

ループを持たない多重グラフを \(G\) とする。次の条件を満たす \(G\) の頂点 \(u\) が存在すると仮定する:

\(G\) の任意の頂点 \(v\) に対して、\(u\) から \(v\) への路が \(G\) に唯一つ存在する。

このとき \(G\) が木だと示せ。

[Remark: 量化子に注目してほしい: この問題では \(\exists u\forall v\) が使われているのに対して、木の同値性定理 (定理 5.2.4) の命題 T2 では \(\forall u\forall v\) が使われている。]

  1. 実際、もし全ての誘導部分グラフが閉路を持たないとすると、\(G\) の閉路は異なる成分をまたぐことになる。しかし成分が異なる頂点の間に歩道は存在しないので、これは不可能である。 ↩︎

広告
このページの文章はテキストゆれないくんを使って校正されました。